基于耦合模型的地質災害易發性分區
——以宜賓市為例

金 帥

（防災科技學院，河北 三河065201）

引言

宜賓市地處云貴川三省交界地帶，地震活動頻繁，地震、降雨加之人為活動導致該地區地質災害發生頻繁，給人民群眾生命財產帶來巨大威脅。地質災害易發性分區不僅可以有效減輕地質災害損失，還可以為各級政府制定地質災害防治規劃和實施地質災害預警提供依據[1]。

目前，地質災害易發性分區方法較多，但沒有統一的評價標準[2，3]。最早為方便評價，研究者試圖通過模糊評判的方法進行易發性分析，此方法主觀因素占主導，結果是否可信常受到質疑[2-5]。薩蒂[5]利用層次分析模型進行易發性評價，通過專家等具有專門知識的人對各評價因子進行重要程度排序，構建比較矩陣并賦予權重值。由于AHP 法往往是通過專家等權威人士進行分析，結果具有公信力[5-6]。由于易發性工作的發展，不依靠主觀因素的客觀評價方法開始涌現，如證據權、Logistics 模型、信息量模型等[2-3]。目前，常用的方法有信息量模型[3]、Logistics 模型[4]、AHP 法[5-6]及人工智能[7]等方法。其中，證據權法考慮了各因子正負兩方面的因素，對因子如何影響滑坡發生有全面的認識，但是計算較為復雜，分區精度不高；Logistics 模型計算量較小，可以方便得到因子權重，模型建立后，只需填入各因子數值就可快速得到某地區易發性概率，但Logistics 模型對因子要求較高，各因子不得有任何相關性，實際中會導致因子選取困難；AHP 法對參與者的專業知識與經驗要求極高，經驗不足會導致精度降低甚至不可用；人工智能的方法計算快速且精度較高，但該方法對參數的調試繁瑣，未經參數調優的模型不可用。由于信息量模型理論簡單，計算方便，既有效避免AHP 法主觀判斷，精度又略高于Logistics 模型[8]，逐漸成為易發性分區主要方法。

信息量模型優點突出但也有缺陷。其只是單純的對各因子圖層進行疊加，忽略了各因子對易發性的貢獻率不同，模型加入過多非主要評價因子往往導致分區精度降低。本文針對易發性評價工作中，單一模型評價有缺陷的問題，選擇常用的信息量模型與Logistics 模型進行耦合。Logistics 模型客觀計算得到的系數表示了各評價因子的重要程度，利用其為信息量模型做權重，彌補信息量模型忽略各因子貢獻率不同的缺陷，降低易發性次要因素比重，以此提高易發性分區精度。

1 研究區概況

宜賓市位于四川省東南，全市面積1.33 萬平方公里，總人口551.5 萬[9]。宜賓市地形由西南向東北逐漸降低，全市地形地貌以山地和丘陵為主，全區地質災害點分布較為分散，但大多集中于海拔中部地區，全市海拔最高與最低處地質災害分布較少。本文共選取宜賓市地質災害點1160 處。其中滑坡603 處，崩塌345 處，崩塌、滑坡及具有發展成崩塌和滑坡的不穩定邊坡共占地質災害點總數的92.32%，表明研究區內主要地質災害為滑坡和崩塌。宜賓地質條件復雜，以石英巖、頁巖、粉砂巖、泥巖為主，玄武巖少量分布。

2 數據來源及因子分析

2.1 數據來源

本文地質災害數據來源于四川省自然資源廳（http：//dnr.sc.gov.cn/scdnr/scxxgkzn/sc_gkzn.shtml），利用ArcGIS轉換成矢量點圖層，研究區內主要地質災害為滑坡與崩塌，經分析，地質災害點在300m～600m 處分布最為廣泛，占全區地質災害點51.5%；地層巖性和斷裂帶來源于中國地質調查總局1：50 萬地質圖，經重投影并矢量化得來；數字高程模型（DEM）來源于NASA，采用12.5mALOS DEM，經鑲嵌和裁剪后重采樣為30m 柵格。地形因子（如坡度、坡向等）根據DEM 得來，其中，平面曲率表示研究區內地形離散度及水流匯集的可能性，是等高線的彎曲程度；剖面曲率表示坡度的再分析，對坡度再次求導得出，是剖面線的彎曲程度；基礎地理數據如路網、水系等來源于天地圖（http：//lbs.tianditu.gov.cn/home.html），其中路網分為鐵路網與公路網，對其進行合并處理；降雨量利用近10 年宜賓地區降水再分析數據，來源于WheatA，經計算各點平均值后使用普通克里金插值得來；地震動峰值加速度（PGA） 來源于《中國地震動參數區劃圖》（GB18306-2015）；興趣點（POI）密度采用爬蟲技術獲得宜賓地區5 萬余處POI，經ArcGIS 密度計算得來；NDVI采用Landsat 8 OLI_TIRS 衛星數字產品，經輻射定標及大氣校正后計算得來；地形因子（坡度、坡向等）來源于ALOS DEM，基于ArcGIS 進行提取。

綜合考慮研究區實際與計算量，結合前人經驗[10]，本文以30m×30m 柵格為評價單元，基于ArcGIS 共劃分為14738029 個柵格。

2.2 評價因子分析

目前，易發性分區因子選取種類與方法日益增多[11]。本文選取DEM、坡度、坡向、PGA、POI 點密度、地形起伏度、坡型、斷層距離、河流距離、道路距離、NDVI、土地利用、巖性、降雨量、剖面曲率，平面曲率共計16 類評價因子，其中，連續型因子以自然斷點法進行分級，非連續性因子以頻率比作為分級依據。

DEM 越高，地質災害發生頻率越高，超過一定海拔高度后，地質災害頻率開始降低，由圖1 可知，研究區內地質災害多分布于海拔300m～600m 處的低山丘陵地帶。

坡度與地質災害發生密切相關，坡度越陡，滑坡體摩擦力越小，滑坡越容易發生，研究區內危險坡度為15°～36°之間。

坡向通過日照時常與蒸發量等因素對地質災害產生影響；由于地質災害觸發因素主要有降水和地震，因此將降雨量與表征地震的地震動峰值加速度和距離斷層距離納入評價因子，由圖可知，研究區降水量自東向西依次增加，與地質災害點分布相吻合，表明降水量是影響地質災害的因素之一。

由于受到人為活動干擾，導致部分地區巖石土體松動或者邊坡穩定性降低，容易發生滑坡等地質災害，故表征人類活動的POI 點密度與道路距離納入評價因子。

河道沖刷會使含水量與坡度等發生變化而導致邊坡失穩，進而發生地質災害，故距河流距離納入評價因子，距河流越近，地質災害發生越頻繁。

評價因子過多會帶來因子冗余，部分因子相關性太強，使得易發性分區精度呈現過飽和的趨勢[12]。為此，本文引入Mahalanobis 距離[13]，利用頻率比作為數值[14]，應用步進式方法進行相關性檢驗。

Mahalanobis 距離表示數據協方差距離，由于其充分考慮了兩組數據集間的特征與聯系，可以利用其計算兩組數據集的相似度，是進行數據相關分析常用方法之一[15]。頻率比（FR）表示分級后的評價因子中，各分級對易發性的影響程度[16]，其定義如下：

圖1 易發性評價因子

其中：N1表示分類內地質災害柵格數；N2表示分類柵格數；S1表示研究區地質災害總柵格數；S2表示研究區總柵格數，當FR>0 表示該分類區間有利于地質災害發生；當FR<0 表示該分類區間不利于地質災害發生（見表1）。Mahalanobis 距離計算基于SPSS 完成。

經因子相關性分析，最終確定12 類因子（巖性、坡度、DEM、地震動加速度、NDVI、斷裂帶距離、降雨量、水系距離、POI 點密度、地形起伏度、坡型、道路距離）顯著性小于0.05，即該12 類因子無相關性，可以進行模型構建（見圖1）。

3 信息量與Logistics 耦合模型

3.1 信息量模型

信息量模型是信息理論延伸出的預測模型，理論基礎是將地質災害各影響因子單獨進行分析。將各因子分級后，各分級狀態對地質災害易發性影響程度不同，影響程度即為信息量，信息量數值可以表示地質災害與影響因子之間的關系[17-18]。

總信息量為：

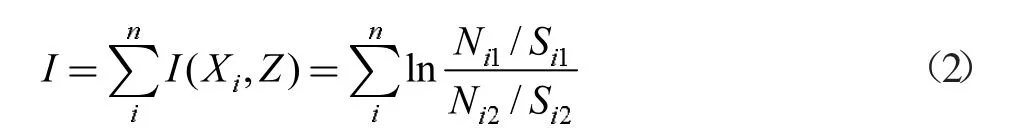
其中，I（Xi，Z）是評價因子Xi（i=1，2，3...）的信息量，其中：N1表示分類內地質災害柵格數；N2表示分類柵格數；S1表示研究區地質災害總柵格數。

信息量值如表1 所示。

3.2 Logistic 模型

Logistic 模型主要應用于醫學領域，屬于線性回歸的一種。其對結果進行二分類，一般結果可用1 和0 代表發生與未發生，由于Logistic 模型對評價因子包容性好，即評價因子可以是連續型變量也可以是非連續型變量且客觀公正，目前廣泛應用于易發性分區中[14]。但Logistic 模型計算繁瑣，進行易發性分區精度不如信息量模型等缺陷也制約其在易發性分區中大規模應用。計算公式為：

其中P 為結果發生的概率，β0為常數項，βi為非常數項系數，使用頻率比，基于SPSS 計算Logistic 模型系數，計算結果見表2。

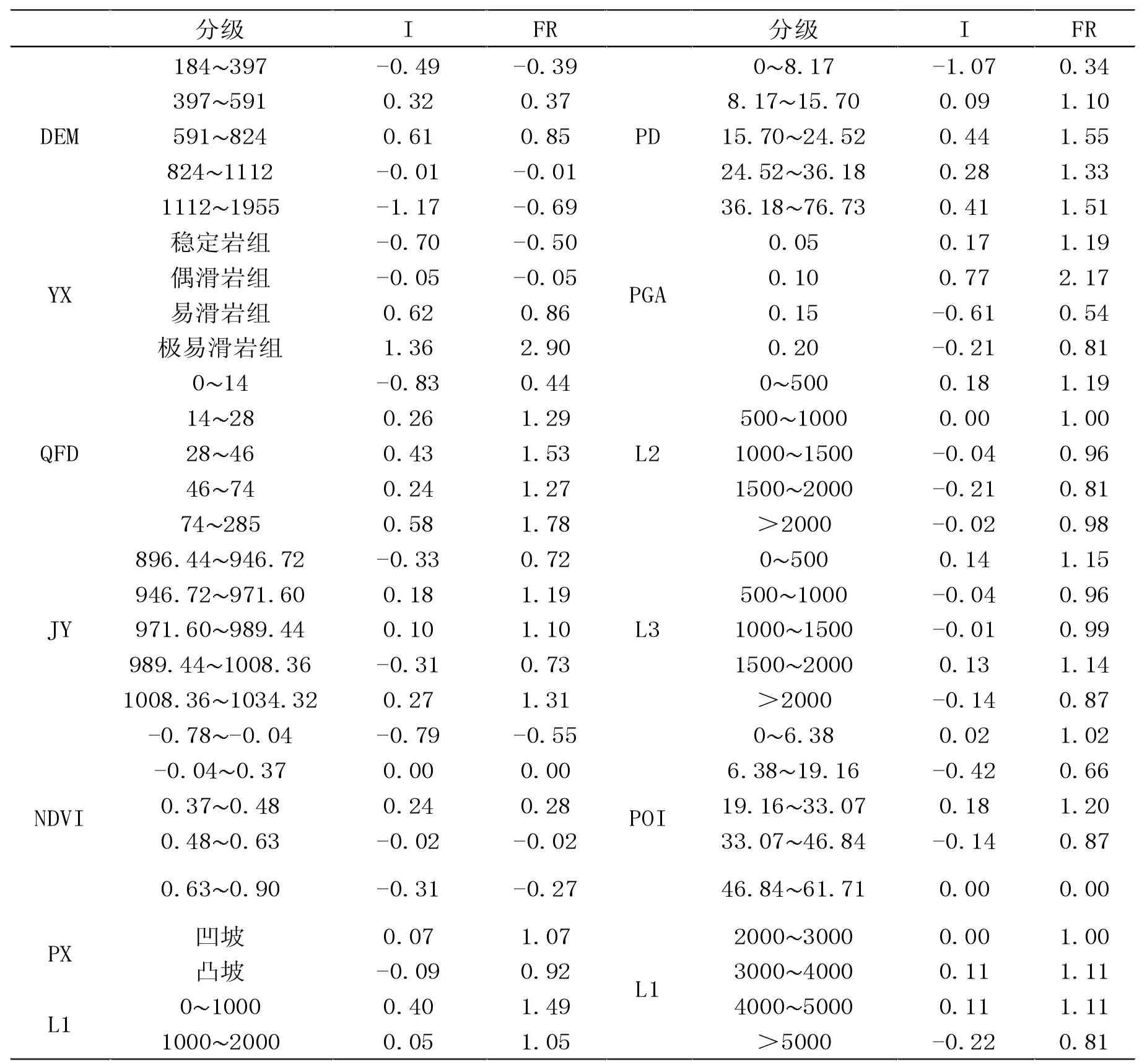
表1 信息量表

表2 Logistic 模型計算表

3.3 信息量與Logistic 耦合模型

針對信息量模型忽略各評價因子對地質災害易發性貢獻率不同的缺陷，采用Logistic 模型系數作為信息量法權重，在ArcGIS 中使用柵格計算器進行圖層計算。

由于使用的Logistic 模型系數是不依賴主觀評判，所以該耦合模型既避免AHP 法主觀定權的缺陷，又保留信息量法精度高、簡單易行、運算速度快的優勢，同時避免Logistic 模型計算繁瑣、精度較低的弊端。計算公式為：

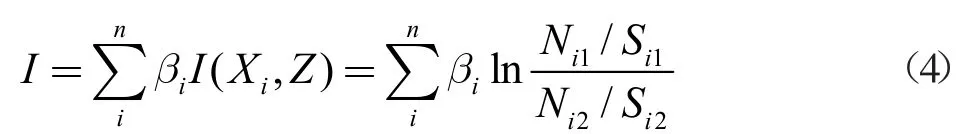
4 易發性評價結果及精度檢驗

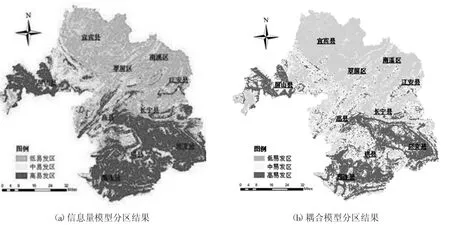
圖2 宜賓市地質災害易發性分區

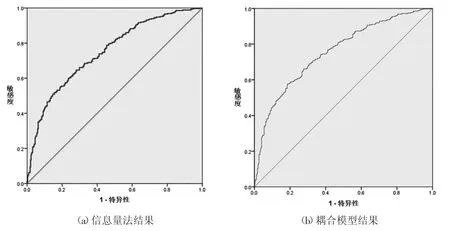
圖3 ROC 曲線

4.1 易發性評價結果

將上述12 類評價因子進行疊加分析，利用自然斷點法將研究區分為三類，分別為低易發區、中易發區和高易發區（見圖2）

從圖2 可知，屏山縣、筠連縣、興文縣地質災害發生頻繁，宜賓縣、翠屏區、南溪區等地質災害發生率低。結合DEM、坡度、巖性等信息可知，高易發區大多位于山區且坡度較陡處，巖性以粉砂巖或者泥巖為主的地區。

信息量模型計算得到的高易發區多于耦合模型得到的高易發區；但兩個模型易發區走勢基本一致，初步證明分區結果準確。

4.2 精度檢驗

本文應用ROC 曲線計算AUC 值進行精度驗證。ROC 曲線又稱為受試者特性曲線，是醫學上常用的關聯性分析方法，其通過設定閾值來表達觀測量與結果的關聯度，關聯度越高，表明觀測值與發生結果越緊密，其精度也越高。AUC 值為ROC 曲線下方與坐標軸構成的面積，對ROC 曲線進行積分運算，值越大表明擬合度越高。由于其簡單便捷，也常常被用來進行易發性分區制圖精度的檢驗[19]。本文綜合前人經驗[19]設定閾值為0.5，通過驗證組數據進行驗證，經計算，信息量模型AUC 值為0.749，信息量-Logistics 耦合模型AUC 值為0.756，結果表明耦合模型精度更高（如圖3）。

5 結果

本文通過信息量模型與Logistics 模型進行耦合，利用Logistics 模型系數表示各評價因子重要程度為信息量模型賦予權重，改進了信息量模型忽略評價因子對易發性貢獻率不同的弊端，提高了易發性分區結果的精度。經計算，信息量模型精度為74.9%，信息量-Logistics 耦合模型精度為75.6%，結果表明耦合模型精度更高，該方法簡單易行，不受人為因素干擾，既保留信息量法計算速度快，原理簡單的優勢，又避免Logistics 模型精度較低，計算繁瑣的弊端，客觀公正，可以作為易發性分區的模型。