關于帶記憶的線性熱彈性板方程解的衰減
米小平, 蒲志林, 趙夕雅
(四川師范大學 數學科學學院,四川成都610066)
1 預備知識
設Ω?R2是一個具有光滑邊界?Ω的區域,考慮如下的Kirchhoff熱彈性薄板方程
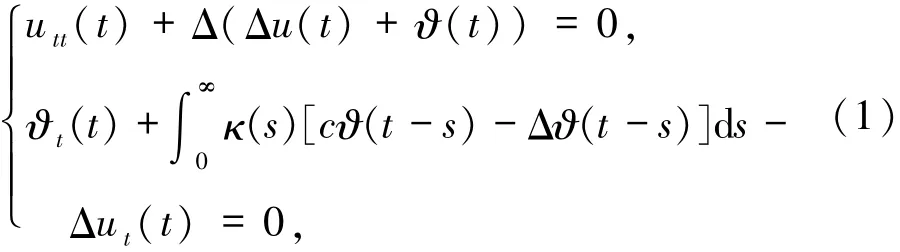
其中,x∈Ω,t∈R+=(0,∞).
根據方程的物理背景,考慮如下邊界條件
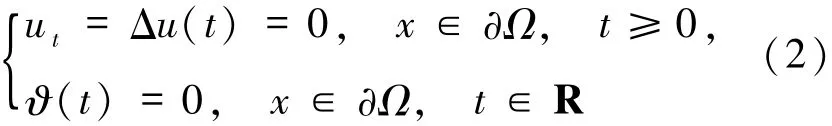
及初始數據
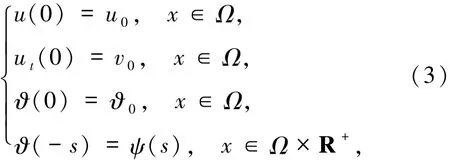
其中,c≥0,函數u0,v0,?0:Ω→R和ψ:Ω×R+→R是給定的函數,未知函數u表示板的垂直位移,而?表示平衡參考值的溫度變化場.為簡便起見,把所有其他物理常數設為1.實際上,在文獻[1-2]最早提出的原始模型中,c>0.Fabrizio等[3]考慮了c=0的情況.
已廣泛研究熱傳導方程中沒有記憶效應的線性熱彈性板[4].在熱通量的傅立葉定律被Gurtin-Pipkin定律取代后,就產生了出現在第一個方程中的卷積項.Giorgi等[1]考慮了解的衰減問題.本文在對記憶核進行非常弱的假設下,根據Hilbert空間上的c0半群,并利用抽象半群理論[4],證明指數穩定性.與我們的模型相比,主要區別是第二個方程中存在一個耗散項,這是因為除了熱通量之外,熱功率還依賴?的過去歷史.
2 記號和假設
設H是Hilbert空間,分別用〈·,·〉H和‖·‖H表示H上的內積和范數,當H=L2(Ω)時省略下標,固定c≥0.給出定義在L2(Ω)上的正定算子A=-Δ和B=cI-Δ,定義域D(A)=D(B)=對r∈R,引入Hilbert空間Hr=D(Ar/2),賦予通常的內積顯然,當r1>r2時為緊嵌入,它在Hr上與〈Br/2·,Br/2·〉為等價內積.
令μ(s)=-κ′(s),μ(s)滿足以下條件:
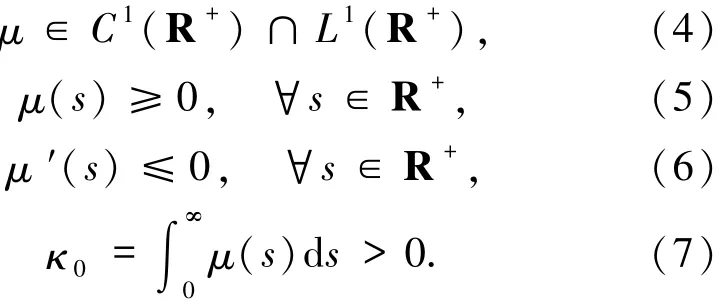
注意(7)式意味著μ不等于零.令σ∞=sup{s|μ(s)>0},也可能σ∞=∞,對于每一個σ<σ∞,通過(4)-(6)式存在一個集合Oσ?(σ,σ∞)具有正的Lebesgue測度,使得
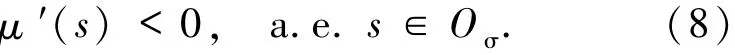
通過(4)和(5)式,對于r∈R,給出加權Hilbert空間
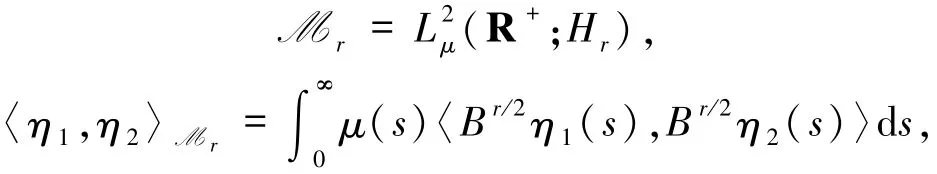
在M1中引入線性算子T:
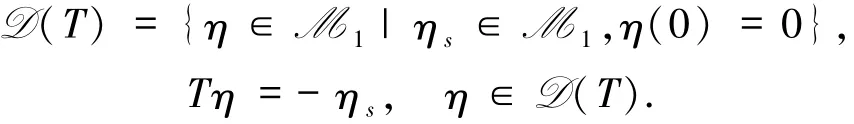
這里ηs是η關于s的偏導數,算子T是C0壓縮半群的無窮小的生成元,特別有
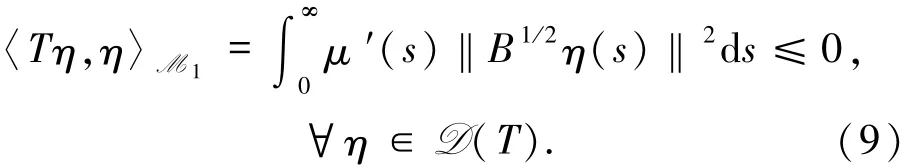
最后定義Hilbert空間
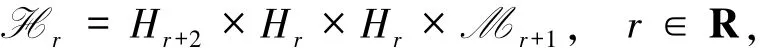
為了后文的需要,對空間Mr的緊致性做一個簡單的介紹.對η∈M1,引入尾部函數
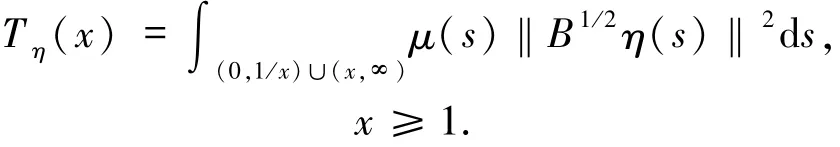
3 抽象線性系統解的衰減性質
設S(t)=etL為Banach空間(H,‖·‖)上的一個線性C0半群,其中L是其無窮小生成元.現在為‖S(t)z0‖→0當t→∞時提供一個簡單的充分條件.
定義3.1[5]稱滿足以下2個條件的S(t)為線性梯度系統:
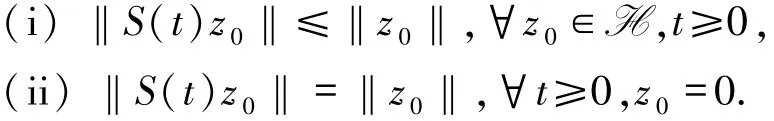
如果S(t)為一個線性梯度系統,那么它必然是一個C0收縮半群.而且線性梯度系統并不是對所有的初始數據都衰減到零.
定理3.2設z0∈H,S(t)為一個線性梯度系統.若集合在H中相對緊,則
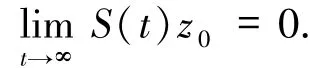
證明令由于集合Bt是非空的、緊的、連通的和嵌套的,則是ω一極限集ω(z0).因而,是非空的、緊的且連通的.選取任意的ζ0∈ω(z0),則存在tn→∞使得S(tn)z0→ζ0.由(i)可知,若存在,則對所有的ζ0∈ω(z0),又ω(z0)是不變的,因此
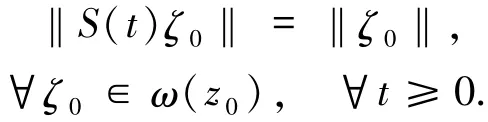
通過(ii)可得ω(z0)={0},從而S(t)z0收斂到0.
推論3.3設S(t)為一個線性梯度系統,?z0∈X,其中X是H的稠密子集.則對于所有的z0∈H,當t→∞時S(t)z0→0.
證明給出z0∈H.對于?ε>0,存在?z0∈X,使得此外存在tε≥0,使得
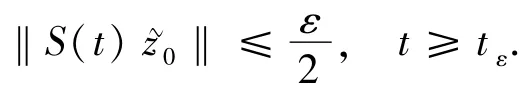
因此
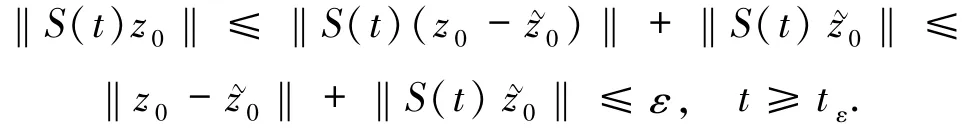
4 解半群與解的衰減
根據文獻[6]的思想,引入一個額外變量,即?的過去歷史總和,定義為形式上滿足方程ηt+ηs=?,s∈Ω,(t,s)∈R+×R+,及邊界條件和初始條件
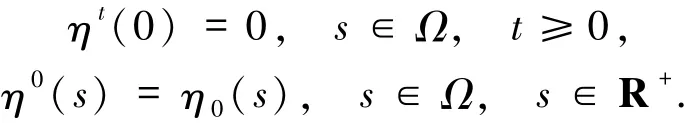
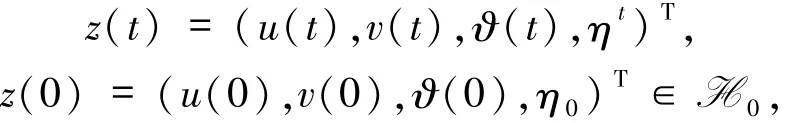
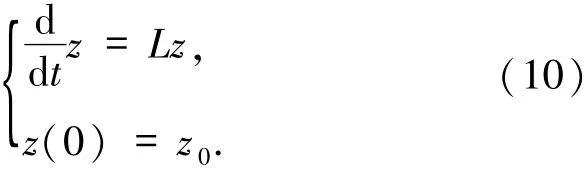
線性算子L定義為
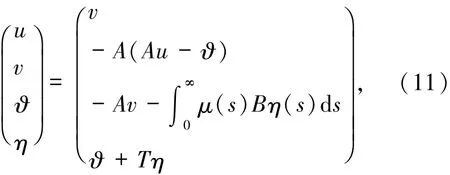
定義域為
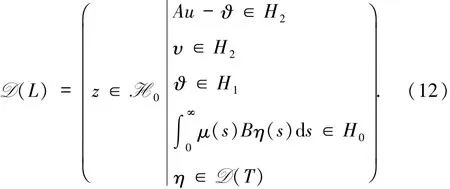
由Lumer-Phillips定理[11]可得到,系統(10)在相空間H0上定義C0線性收縮半群S(t)=etL.由(6)式可知
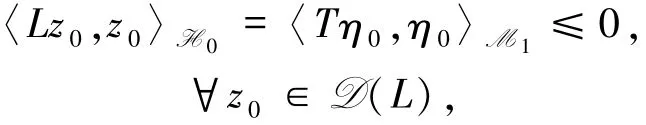
明確表示I-L將D(L)映射到H0.
系統(10)是通過分部積分得到的,實際上等同于最初始的問題,此外,解的分量有明確的表示公式:
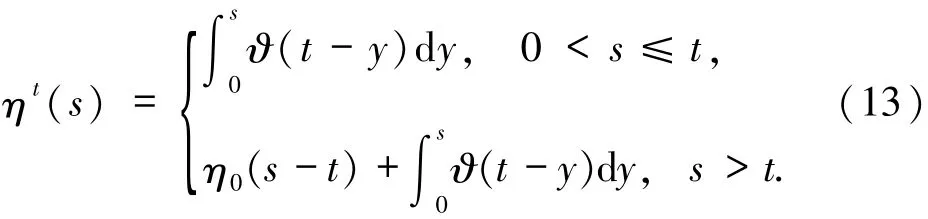
定理4.1S(t)是H0上的線性梯度系統.
證明如果存在z0∈H0和任意的t≥0,使得‖S(t)z0‖H0=‖z0‖H0成立,根據(9)式發現

任取σ<σ∞.由于上述方程和(8)式是等價的,對于任意的t≥0,ηt≡0在Oσ上幾乎處處成立.根據(12)式,對于任意的t≥0,?(t)≡0(注意s和?是無關的).根據(13)式有
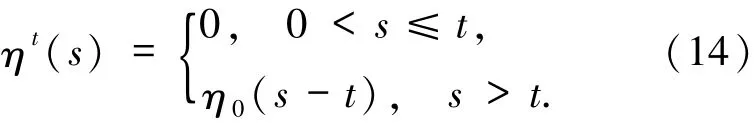
但這意味著η0≡0幾乎處處成立,至少應該在區間(0,σ)上.根據σ的任意性的確可以得知η0≡0幾乎處處成立.
引理4.2[7]設C?M1滿足:
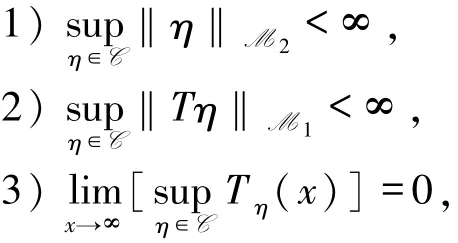
則C在M1中相對緊.
證明系統(10)具有足夠的耗散性,可以使得任何軌跡衰減到零,在μ具有較弱的衰減性條件下.
定理4.3假設條件(4)-(7)式滿足,如果存在δ>0,使得

證明固定z0∈D(L)∩H1,用C=C(z0)≥0來表示一個一般的常數.特別地,對于?t≥0,有z(t)=S(t)z0∈D(L),將由下列步驟完成定理的證明.
第一步
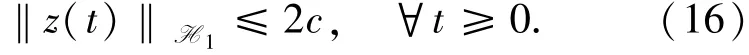
事實上,在H0上引入對角算子?B=BIH0.根據(10)式和?Bz可得
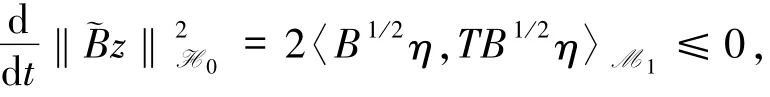
根據(9)式可得
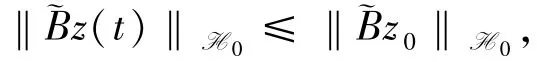
第二步
本研究采用綜合心理護理方法,在以人為本護理理念指導下,充分了解患者需求和存在的問題,為其提供心理護理,干預人員與患者建立互信平等的朋友關系,為實施心理護理奠定基礎。

事實上,根據(13)式可得
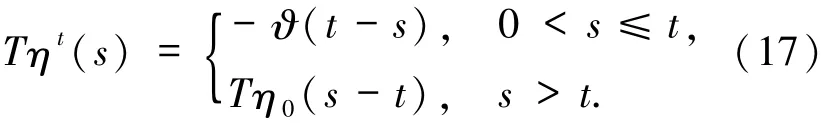
利用(16)和(7)式可得
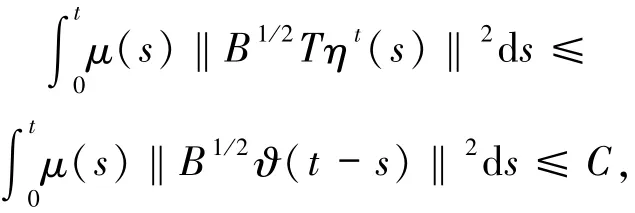
而且由于(6)式可得
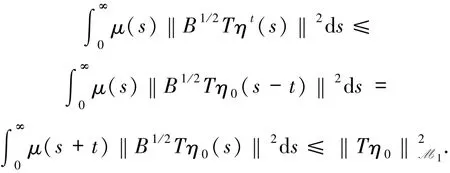
根據以上2個結論,可得第三步.
第三步
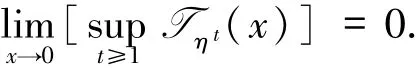
定義
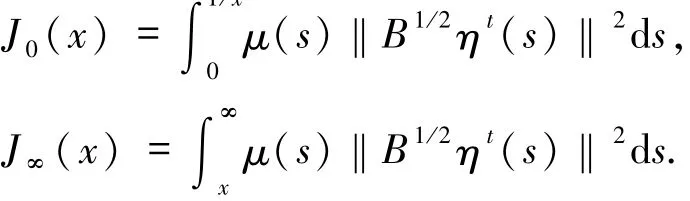
很明顯
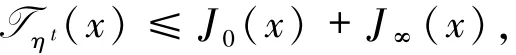
由第一步結論和(7)式可得
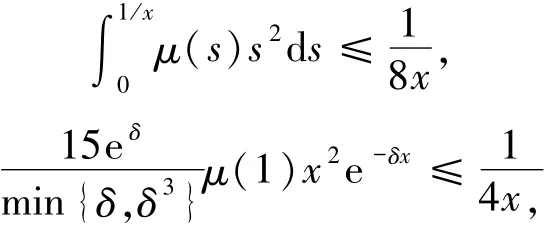
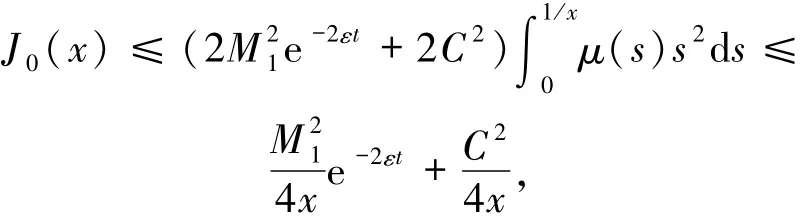
因此,當t1=t1(M1)≥1時,
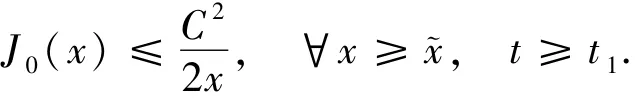
則當x→∞時,J0(x)→0.
根據(13)式和Young不等式可得
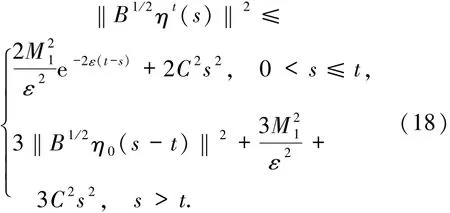
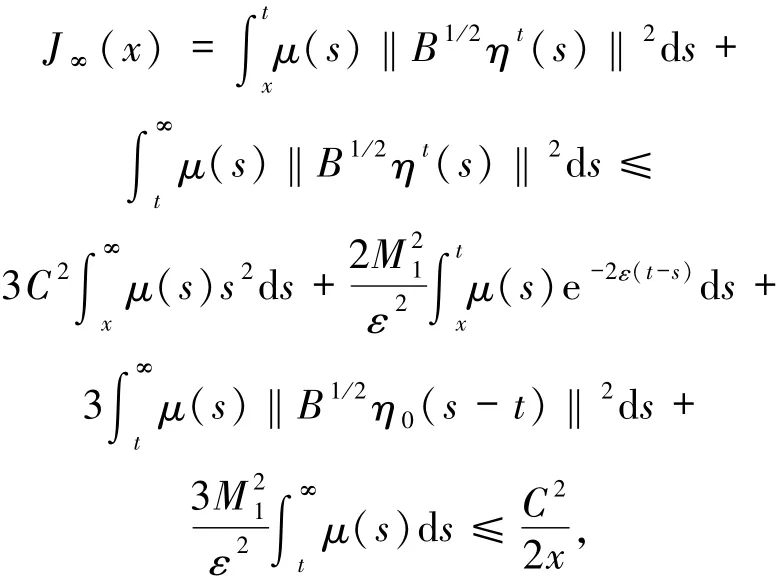
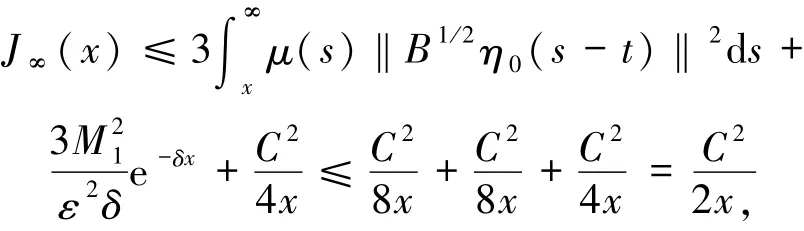
可知當x→∞時,J∞(x)→0.

