關于轉子系統動平衡試重選擇的試驗研究

解夢濤，翟亞浩

(中國飛行試驗研究院發動機所，陜西 西安 710089)

0 引言

轉子系統在零部件生產制造及裝配過程中會不可避免地產生偏心質量[1-2]，因此多數轉子系統會要求裝配完成后進行動平衡操作以降低整機振動水平，減小支撐系統結構載荷，對于高速、重載機械系統一般會在使用階段視情況進行在線動平衡以延長設備使用壽命[3-4]。而工程中采用的轉子動平衡原理多是根據影響系數法進行[5-6]，即需要先在轉子系統上添加試重，通過與初始構型下的不平衡量進行比對以計算出轉子影響系數矩陣，如式(1)所示。再計算出所需的配平方案。

(1)

其中，轉子系統的初始不平衡振動為V0，加試重后的不平衡振動為V1，影響系數矩陣為A，加裝的試重為W1。所有變量均為復數，包含幅值與相位信息。

因此，影響系數矩陣的準確與否直接關系到動平衡計算精度，而多篇研究文獻表明加裝試重的選取直接關系到影響系數矩陣計算的準確度[7-8]。本文通過試驗研究對比分析了試重大小及加裝方位對動平衡計算結果的影響規律。

1 轉子動平衡試驗

圖1 地面轉子試驗臺實物圖

本文開展的轉子動平衡試驗在圖1所示的地面轉子試驗臺上進行。轉子試驗臺由鑄鐵平臺、驅動電機、葉盤-轉軸系統、軸承支撐-潤滑系統及測試系統五個主要部分組成。

為準確測量轉子系統不平衡量，在轉子系統轉速范圍內選取9個轉速點(表1)進行轉速臺階試驗，測量計算每個轉速點處的轉子不平衡振動。

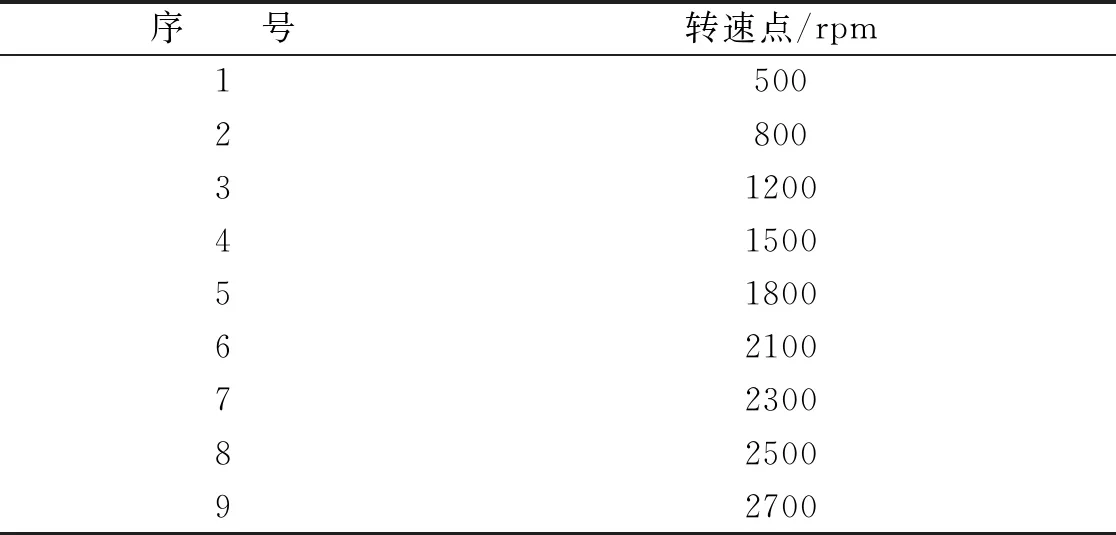
表1 轉子動平衡試驗轉速點設置

最終，計算獲取的轉子不平衡振動如圖2所示(初始構型為例)。

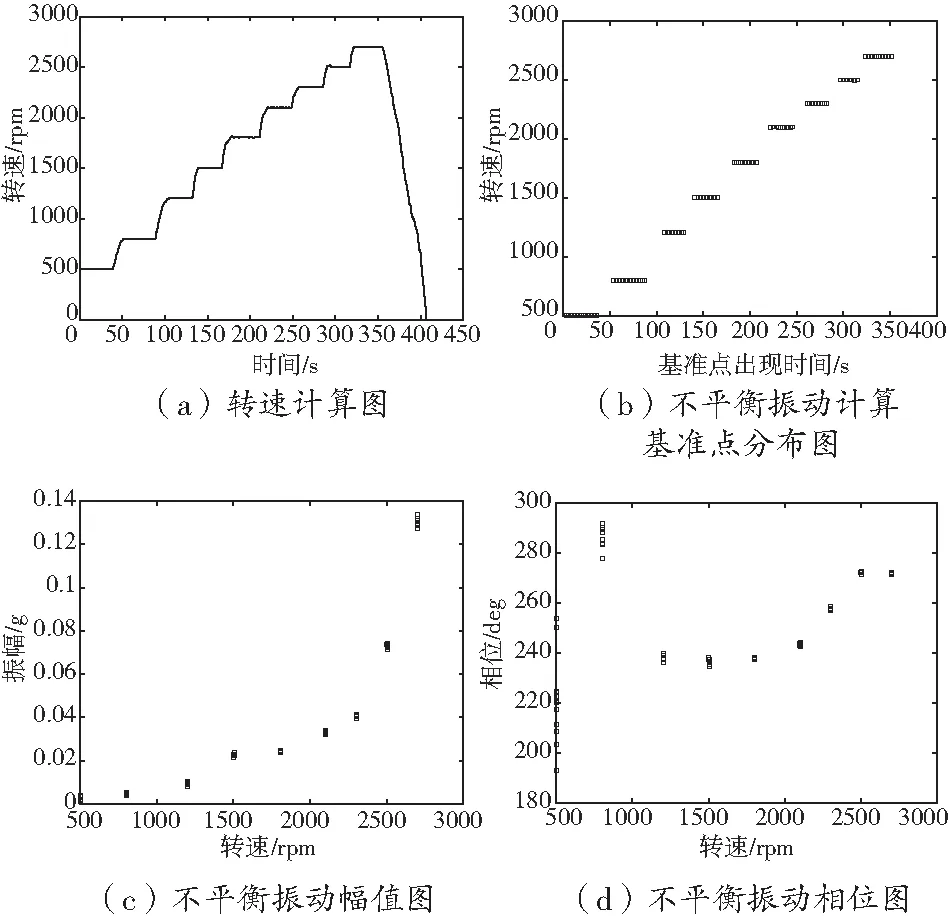
圖2 初始構型下試驗獲取的轉子系統不平衡振動

其中，圖2(a)為試驗轉速曲線圖；圖2(b)為每個試驗轉速點下提取的不平衡振動計算基準點，即檢測到轉速達到一定的穩定條件后選擇的不平衡振動計算基準時間點分布圖，表明在每一個轉速臺階處均存在多個計算基準點，將會計算出多個不平衡振動幅值及相位數據；圖2(c)、(d)分別為計算獲取的轉子不平衡振動幅值與相位信息。可知根據各轉速點不同時段數據計算的不平衡振動幅值信息均較為穩定，不平衡相位信息在1200 rpm以上也較為穩定。在低轉速區間不平衡振動幅值接近于零，表示轉子系統幾乎不存在初始彎曲，不平衡振動可直接用于動平衡計算。

為分析加裝試重的大小與相位對于轉子動平衡結果的影響，分別在轉子風扇盤90°、210°、330°三個方向分別加裝6.93 g與12.41 g兩種質量的試重后進行不平衡錄取試驗。圖3為配重加裝現場圖。

最終，可根據各轉速點下各不平衡幅值與相位信息繪制出轉子不平衡幅頻與相頻曲線，如圖4所示。

圖3 配重加裝現場圖

可獲得初始構型與6組試重構型下的轉子系統幅頻與相頻特性曲線，如圖4所示。

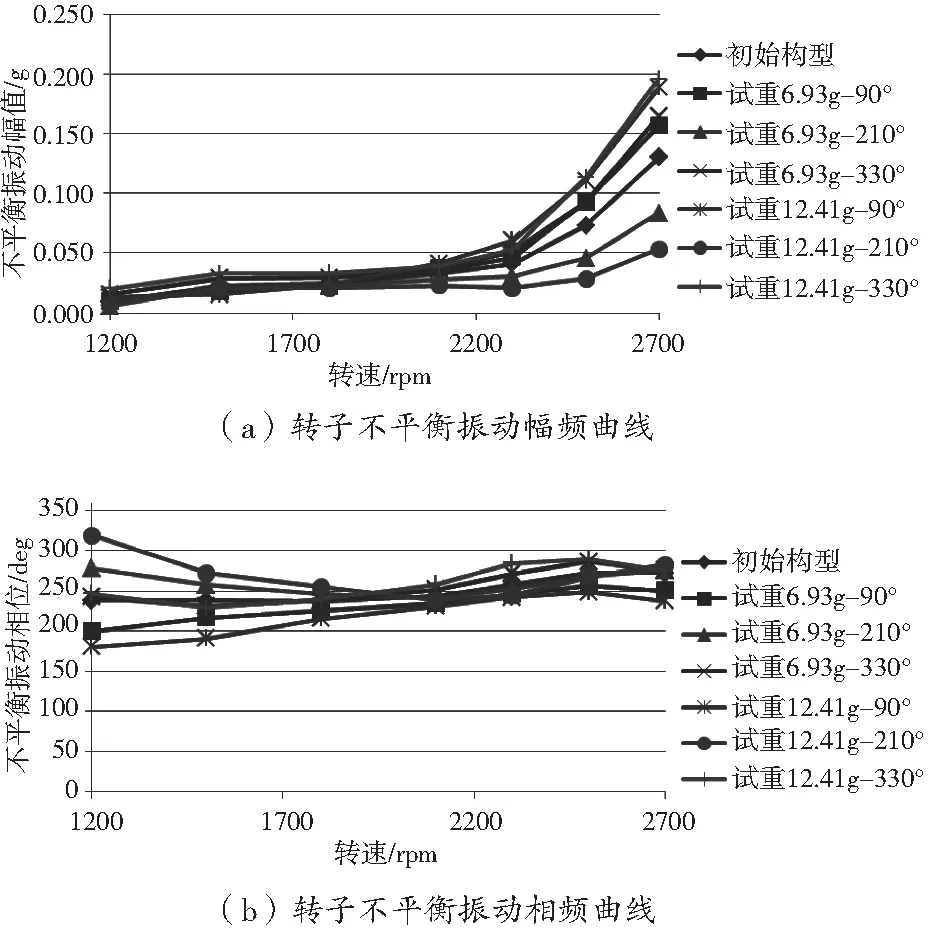
圖4 轉子系統在初始與試重構型下的不平衡特性曲線

2 試重對動平衡結果的影響分析

為分析不同試重加裝方案對轉子動平衡精度的影響，分別以初始及試重6.93g∠90°試驗、初始及試重6.93g∠210°試驗、初始及試重6.93g∠330°試驗、初始及試重12.41g∠90°試驗、初始及試重12.41g∠210°試驗、初始及試重12.41g∠330°試驗中2700 rpm試驗點的不平衡振動數據為依據，計算影響系數矩陣及配平方案，并進行動平衡試驗，分析試重的大小及加裝相位對動平衡結果的影響。最終，動平衡試驗結果如表2。

表2 試重大小/相位對動平衡結果的對比分析

從6組結果可知，試重大小對動平衡精度的影響較小，而試重方位對動平衡結果的影響很大，當試重加裝方位與轉子的初始不平衡相位較接近時，所計算的影響系數矩陣越準確，動平衡精度較高，反之則動平衡計算精度較低，甚至可能導致動平衡失敗。

3 結論

針對轉子系統動平衡問題，本文為提高動平衡精度，減少動平衡試驗次數，通過地面試驗臺試驗研究了試重加裝方案選擇對動平衡結果的影響。最終，通過不同大小及加裝相位的試重進行對比試驗，結果表明試重大小對動平衡精度的影響較小，而試重相位對動平衡結果的影響很大，當試重加裝方位與轉子的初始不平衡相位較接近時，所計算的影響系數矩陣較為準確，動平衡精度較高，反之可能導致轉子動平衡失敗。