高速旋轉(zhuǎn)炮彈寬海拔彈道解算方法

丁天寶， 何朝， 王良明， 林智偉

(1.西北機(jī)電工程研究所, 陜西 咸陽(yáng) 712099; 2.南京理工大學(xué) 能源與動(dòng)力工程學(xué)院, 江蘇 南京 210094)

0 引言

以射表為基礎(chǔ)計(jì)算火控射擊諸元是高炮武器的傳統(tǒng)方法，具有快速、便捷、準(zhǔn)確等特點(diǎn)，被廣泛應(yīng)用[1]。以前，我國(guó)高炮武器高原射表多以平原低海拔試驗(yàn)結(jié)果為基礎(chǔ)，經(jīng)過(guò)簡(jiǎn)單轉(zhuǎn)換而來(lái)，在高原實(shí)際射擊結(jié)果誤差較大[2-4]。

高炮平原彈道和高原彈道差異很大[5]。以某高炮為例，45°射角、斜距離4 000 m，海拔0 m和海拔4 500 m彈道高度差如圖1所示。

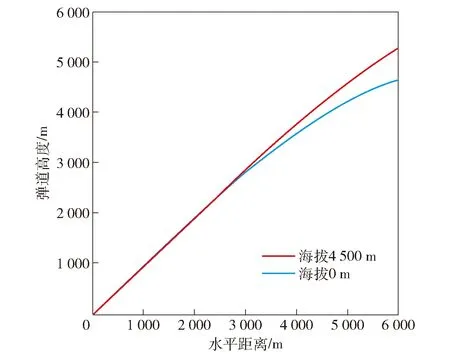
圖1 某高炮高原彈道與平原彈道差異Fig.1 Difference between plateau and plain ballistics of antiaircraft gun

目前，寬海拔射表編擬技術(shù)存在以下問(wèn)題：

1)常用高炮武器射表基于平原射擊結(jié)果編制，在平原地區(qū)的射表精度能夠保證。由于高原特殊的地理環(huán)境和復(fù)雜的天氣條件，高原彈道試驗(yàn)困難；在高原靶場(chǎng)未建成之前，無(wú)法開(kāi)展射表試驗(yàn)[6]。

2)采用4自由度修正質(zhì)點(diǎn)彈道模型解算彈道時(shí)，增加考慮彈丸自轉(zhuǎn)運(yùn)動(dòng)和與此相關(guān)的彈丸動(dòng)力平衡角計(jì)算模型。但是在高射角時(shí)，動(dòng)力平衡角近似計(jì)算會(huì)有較大誤差[7]。

3)傳統(tǒng)高炮武器射表基于零海拔編制，一般采用炮兵標(biāo)準(zhǔn)氣象條件[8-9]，射表中的修正量計(jì)算方法是線(xiàn)性近似微分法。零海拔射表中的各個(gè)修正系數(shù)在高原條件下偏差量較大，會(huì)造成較大誤差。

4)傳統(tǒng)射表編擬時(shí)，海拔高度變化沒(méi)有充分考慮雷諾數(shù)變化對(duì)彈丸阻力系數(shù)的影響[10]。

5)高原空氣稀薄、干燥，阻力小，彈丸起始擾動(dòng)衰減慢，起始擾動(dòng)和彈丸姿態(tài)運(yùn)動(dòng)變化對(duì)平均彈道的影響考慮不充分。

6)彈丸轉(zhuǎn)速影響其姿態(tài)，彈丸旋轉(zhuǎn)速度越高，其陀螺效應(yīng)越強(qiáng)，彈丸攻角隨彈道上升變化大，隨之影響飛行過(guò)程所受阻力，反過(guò)來(lái)進(jìn)一步影響其動(dòng)態(tài)穩(wěn)定性。

7)即使有了平原射表和簡(jiǎn)易高原射表，在高原和平原海拔分界線(xiàn)(3 000 m)上下[11]，射表誤差相對(duì)較大，單獨(dú)使用某個(gè)射表時(shí)會(huì)引入原理誤差。

為了解決上述高原和寬海拔彈道解算中的問(wèn)題，本文提出高速旋轉(zhuǎn)炮彈寬海拔彈道解算和射表研制方法。創(chuàng)建彈丸非線(xiàn)性姿態(tài)運(yùn)動(dòng)模型，用于解決高速旋轉(zhuǎn)彈起始擾動(dòng)所導(dǎo)致姿態(tài)運(yùn)動(dòng)在高原空氣稀薄時(shí)衰減較慢對(duì)平均彈道影響；創(chuàng)建彈丸阻力系數(shù)隨海拔變化模型、彈道符合系數(shù)與射角關(guān)系模型，用于解決高原彈道阻力隨海拔非線(xiàn)性變化對(duì)彈道解算的影響。結(jié)合高平原射表階梯抑制方法，形成了適應(yīng)寬海拔(0～4 500 m)的高精度彈道解算和射表研制新方法。

1 彈道解算數(shù)學(xué)模型

1.1 影響高原彈道解算的主要因素

影響高原彈道解算的主要因素有：

1)高原彈丸姿態(tài)運(yùn)動(dòng)；

2)高原雷諾數(shù)隨海拔變化；

3)高原氣象條件。

在傳統(tǒng)彈道模型中，對(duì)彈丸起始姿態(tài)運(yùn)動(dòng)影響和雷諾數(shù)隨海拔變化通常不予考慮。彈丸起始擾動(dòng)在高原空氣稀薄時(shí)，衰減很慢，對(duì)平均彈道有較大的影響。雷諾數(shù)隨海拔高度不同而變化，阻力系數(shù)隨海拔高度變化。通過(guò)研究發(fā)現(xiàn)，這些因素是造成用平原彈道模型外推高原彈道的主要誤差來(lái)源。因此，為了保證高原彈道解算的準(zhǔn)確性，必須充分考慮彈丸起始姿態(tài)運(yùn)動(dòng)和雷諾數(shù)隨海拔變化對(duì)彈道的影響。

1.2 彈丸剛體運(yùn)動(dòng)微分方程組

把彈丸作為剛體時(shí)，描述其6自由度運(yùn)動(dòng)的微分方程組如(1)式[12-13]所示:

(1)

式中：m和v分別為彈丸質(zhì)量和彈丸質(zhì)心飛行速度；Fxv、Fyv、Fzv分別為作用在彈丸上的合力F在速度坐標(biāo)系Oxvyvzv中的投影；θ和ψ分別為彈道傾角和彈道偏角；x、y、z為彈丸質(zhì)心的空間坐標(biāo)；φ?和φψ分別為彈丸俯仰角和偏航角；ωξ、ωη、ωζ分別為彈丸總的轉(zhuǎn)動(dòng)角速度ω在彈軸坐標(biāo)系Oξηζ中的投影；Mξ、Mη、Mζ分別為作用在彈丸質(zhì)心上的合力矩M在彈軸坐標(biāo)系Oξηζ中的投影；r為彈丸旋轉(zhuǎn)方位角；A和C分別為彈丸的赤道轉(zhuǎn)動(dòng)慣量和極轉(zhuǎn)動(dòng)慣量。

實(shí)際彈丸姿態(tài)運(yùn)動(dòng)包括兩類(lèi)：一類(lèi)是確定性的，如旋轉(zhuǎn)穩(wěn)定彈丸由重力等引起的姿態(tài)運(yùn)動(dòng)；另一類(lèi)隨機(jī)性的，如旋轉(zhuǎn)穩(wěn)定彈由起始擾動(dòng)引起的姿態(tài)運(yùn)動(dòng)等。采用6自由度剛體彈道模型時(shí)，模型中彈丸姿態(tài)運(yùn)動(dòng)和質(zhì)心運(yùn)動(dòng)是完全耦合的，求解確定性的姿態(tài)運(yùn)動(dòng)及其對(duì)彈道的影響比較有效。但是，為了求解隨機(jī)性的姿態(tài)運(yùn)動(dòng)及其對(duì)彈道的影響，在原有彈道模型基礎(chǔ)上附加姿態(tài)運(yùn)動(dòng)計(jì)算模型聯(lián)合解算更加有效。

1.3 彈丸非線(xiàn)性姿態(tài)運(yùn)動(dòng)模型

在高炮彈道解算中，要求準(zhǔn)確解算平均彈道，而不是解算每條隨機(jī)彈道。隨機(jī)性的姿態(tài)運(yùn)動(dòng)造成彈道系統(tǒng)偏差，這是平均彈道計(jì)算應(yīng)該考慮的。

隨機(jī)性姿態(tài)運(yùn)動(dòng)對(duì)彈道的系統(tǒng)影響可以某種等效擾動(dòng)源引起的姿態(tài)運(yùn)動(dòng)來(lái)計(jì)算，能反映彈丸在某段彈道上隨機(jī)姿態(tài)運(yùn)動(dòng)的平均過(guò)程，從而準(zhǔn)確計(jì)算出該段彈道上阻力系數(shù)的變化，有利于計(jì)算不同海拔上的彈道計(jì)算精度。在高速旋轉(zhuǎn)炮彈寬海拔彈道解算中，建立的附加非線(xiàn)性姿態(tài)運(yùn)動(dòng)模型為

(2)

式中：δζ和δη為彈丸的攻角分量；d為彈徑；ρ為空氣密度；S為彈丸特征面積；CLα、CNpα、CMα、CMq、CMpα分別為彈丸的升力系數(shù)、馬格努斯力系數(shù)、靜力矩系數(shù)、赤道阻尼力矩系數(shù)和馬格努斯力矩系數(shù)的導(dǎo)數(shù)。

2 彈道阻力系數(shù)計(jì)算模型

2.1 彈丸阻力系數(shù)計(jì)算模型

彈丸阻力系數(shù)一般可表示為

(3)

式中：fD為阻力符合系數(shù)；Cx0為零升阻力系數(shù)；ΔCxRe為雷諾數(shù)影響引起的阻力系數(shù)增量；Cxδ2為攻角誘導(dǎo)阻力系數(shù)；δp為確定性姿態(tài)運(yùn)動(dòng)引起的攻角；δd為隨機(jī)性姿態(tài)運(yùn)動(dòng)引起的攻角。

2.2 雷諾數(shù)對(duì)彈丸阻力系數(shù)影響計(jì)算模型

雷諾數(shù)對(duì)彈丸阻力系數(shù)的影響機(jī)理非常復(fù)雜，嚴(yán)格來(lái)說(shuō)與彈丸幾何形狀、表面狀況、馬赫數(shù)以及氣流與彈丸表面間的熱交換等有關(guān)。實(shí)際情況下要同時(shí)考慮這些因素的影響是非常復(fù)雜的。為了在高原彈道計(jì)算中盡可能準(zhǔn)確地考慮雷諾數(shù)的影響，可采用如(4)式模型：

(4)

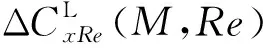
2.3 彈道符合系數(shù)與射角關(guān)系模型

射角不同彈丸飛行高度不同，因?yàn)閺?fù)雜的彈丸姿態(tài)運(yùn)動(dòng)，飛行高度對(duì)彈丸阻力系數(shù)的影響機(jī)理非常復(fù)雜，為了彈道計(jì)算準(zhǔn)確，需要引入彈道符合系數(shù)。假設(shè)測(cè)出一條彈道上不同時(shí)刻tk所對(duì)應(yīng)的空間坐標(biāo)數(shù)據(jù)(xk,yk,zk),k=1,2,…,n，記xk=(xkykzk)T。

各個(gè)符合系數(shù)用向量C可表示為

C=(ωγfDfLfMz)T，

(5)

式中：ω為高低跳角；γ為方向跳角；fL為升力系數(shù)的符合系數(shù)；fMz為靜力矩系數(shù)的符合系數(shù)。

采用6自由度彈道方程進(jìn)行全面符合計(jì)算，對(duì)未知參數(shù)C的每一組合理取值，由(5)式可求解得到對(duì)應(yīng)的X(t,C1,C2,…，Cns)，ns=5，其中彈丸的空間坐標(biāo)x(t,C1,C2,…，Cns)=(xyz)T。采用改進(jìn)的高斯牛頓(G-N)迭代法對(duì)上述過(guò)程進(jìn)行迭代，可提高未知參數(shù)C的估計(jì)值的精度。

不同射角下符合系數(shù)的結(jié)果存在差異，可將其擬合成隨射角θ0變化的函數(shù)，如

C=(ωγfDfLfMz)T=C(θ0).

(6)

用隨射角變化的彈道符合系數(shù)來(lái)補(bǔ)償因?yàn)椴煌浣亲枇ο禂?shù)的計(jì)算偏差。

3 高平原射表交接階梯抑制方法

由于高炮外彈道受到很大非線(xiàn)性因素的影響，平原低海拔和高原高海拔射表銜接時(shí)，射擊方位角、射角、彈丸飛行時(shí)間等相關(guān)變量有一個(gè)突變(階梯)，引起火控解算附加誤差，進(jìn)而影響射擊精度。因此，根據(jù)射表參數(shù)變化規(guī)律擬合曲線(xiàn)，采用高平原階梯抑制方法，對(duì)相關(guān)參數(shù)進(jìn)行加權(quán)組合，可提高射表精度。

在海拔0～2 000 m直接采用平原射表解算的射擊諸元(即平原射擊諸元加權(quán)系數(shù)為1，高原射擊諸元加權(quán)系數(shù)為0)；在海拔2 000～4 000 m之間，在平原和高原射表解算的結(jié)果基礎(chǔ)上按照海拔高度相對(duì)海拔2 000 m的變化進(jìn)行加權(quán)組合，取其加權(quán)優(yōu)化后的結(jié)果作為最終的高炮火控系統(tǒng)射擊諸元預(yù)解算結(jié)果；在海拔4 000 m以上直接采用高原射表解算的射擊諸元(即平原射擊諸元加權(quán)系數(shù)為0，高原射擊諸元加權(quán)系數(shù)為1)。具體模型為

(7)

式中：β和ε分別為加權(quán)后的高炮方位角和高低角；βp和βg分別為平原射表和高原射表確定的方位角；εp和εg分別為平原射表和高原射表確定的高低角；λp和λg為加權(quán)優(yōu)化系數(shù)；H為當(dāng)前海拔高度。

試驗(yàn)結(jié)果表明，采用高平原階梯抑制方法，在海拔2 000～4 000 m之間的銜接高度范圍，可在原射擊精度基礎(chǔ)上提高高炮射擊精度10%以上。

4 高原射表計(jì)算與試驗(yàn)驗(yàn)證

通過(guò)建立的彈道模型解算理論彈道，采用實(shí)彈射擊試驗(yàn)測(cè)量實(shí)際彈道參數(shù)，通過(guò)仿真分析理論彈道的差異，進(jìn)而對(duì)高原彈道進(jìn)行符合計(jì)算，提高彈道解算精度。

在青藏高原某海拔4 500 m靶場(chǎng)完成高原彈道試驗(yàn)，分別對(duì)15°、45°和70° 3個(gè)射角進(jìn)行了精確彈道測(cè)量。

試驗(yàn)中，精確測(cè)量了火炮的射角和射向；采用氣象雷達(dá)車(chē)測(cè)量了高空和地面的氣象條件，包括氣溫、氣壓、濕度、風(fēng)速和風(fēng)向等；采用初速雷達(dá)測(cè)量了每發(fā)彈丸的初速；采用彈道跟蹤雷達(dá)，測(cè)量了每發(fā)彈丸彈道上各點(diǎn)的飛行速度和空間坐標(biāo)。

采集上述數(shù)據(jù)，經(jīng)過(guò)彈道符合計(jì)算，一方面可修正基礎(chǔ)數(shù)據(jù)；另一方面，以射表試驗(yàn)點(diǎn)的符合計(jì)算結(jié)果作為支撐點(diǎn)，通過(guò)曲線(xiàn)擬合技術(shù)得到各符合系數(shù)與射角的關(guān)系。

試驗(yàn)結(jié)果：采用平原射表射表時(shí)，在海拔4 500 m、斜距離4 000 m內(nèi)統(tǒng)計(jì)，相同彈丸飛行時(shí)間的彈道空間差為399 m，與其斜距離(4 000 m)的比值為9.98%；使用本文彈道解算方法研制的高原射表，相同彈丸飛行時(shí)間的彈道空間差為1.12 m，與其斜距離(4 000 m)的比值為0.03%，典型數(shù)據(jù)如表1所示。

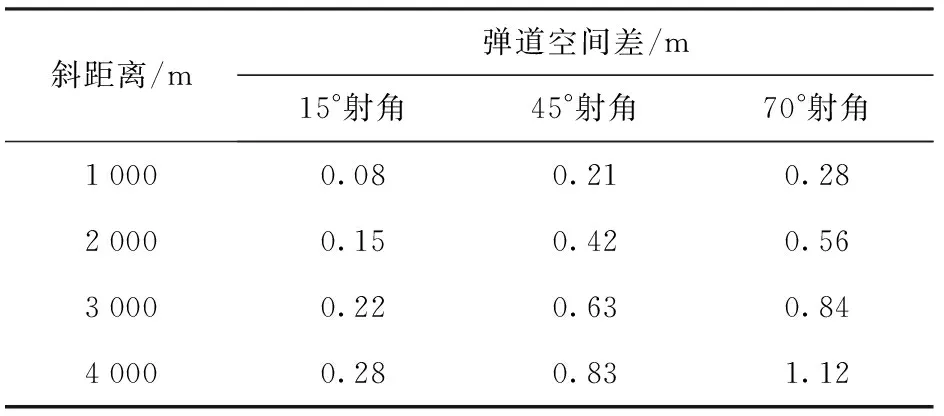
表1 高原射表試驗(yàn)結(jié)果與仿真結(jié)果的彈道空間差

5 結(jié)論

本文建立了耦合彈丸非線(xiàn)性性姿態(tài)運(yùn)動(dòng)方程的彈丸6自由度動(dòng)力學(xué)模型、隨海拔高度變化彈丸阻力系數(shù)模型、彈道符合系數(shù)與射角關(guān)系模型，以此為基礎(chǔ)建立了高原彈丸彈道理論模型，創(chuàng)建了高速旋轉(zhuǎn)炮彈高原彈道解算新方法。此外，為了消除平原射表和高原射表在銜接高度段的原理誤差，創(chuàng)建了高平原階梯抑制控制方法，進(jìn)一步提高了在2 000～4 000 m海拔高度范圍的高炮射擊諸元精度。

該高速旋轉(zhuǎn)炮彈寬海拔彈道解算方法的正確性已經(jīng)被某自行高炮寬海拔射擊試驗(yàn)證明。采用本文高速旋轉(zhuǎn)炮彈寬海拔彈道解算方法所研制的高原射表已經(jīng)推廣應(yīng)用至數(shù)款新型高炮防空武器，提高了應(yīng)用裝備的寬海拔作戰(zhàn)毀殲概率。