關系數據庫中聚合代數約束的高效發現算法
——AAC-Hunter

，2 ，2* ，2

（1.浙江大學計算機科學與技術學院，杭州 310027；2.浙江省大數據智能計算重點實驗室（浙江大學），杭州 310027）

0 引言

給定一個關系數據庫，聚合代數約束（Aggregation Algebraic Constraint，AAC）是一個定義在該數據庫中兩列的聚合運算結果之間的模糊代數約束。聚合代數約束僅約束數據庫中的大多數而非全部記錄。

本文研究如何從關系數據庫中自動發現聚合代數約束。該技術在智慧審計領域具有廣泛的應用前景。考慮一個簡化的報銷數據表，該表包含5個字段：（員工，部門，交通費，住宿費，雜費），表中每一條記錄是包含上述5 個字段信息的報銷記錄。審計員希望從該表中找出違規的報銷記錄，該審計過程能夠順利實施的關鍵在于審計員能否發現報銷數據表中存在的模糊約束，即作用于數據表中的大多數而非全部記錄之間的約束。如果模糊約束的邏輯較簡單，則一般可以通過專家經驗給出。例如，如果審計員通過先驗知識得知大多數正常的報銷記錄滿足如下約束：交通費+住宿費＜1 000，那么該審計員可以通過標準的結構化查詢語言（Structured Query Language，SQL）找出違反上述約束關系的記錄集，然后逐一檢查該記錄集每一條記錄是否是違規報銷。

然而，如果報銷數據表存在聚合代數約束，由于聚合代數約束中包含聚合運算且和數據表中數據的分布高度相關，審計員很難通過通用的先驗知識發現該約束。報銷數據表中的一個聚合代數約束c1如下所示：

該聚合代數約束表明，按照部門字段對報銷記錄進行分組，大多數部門的平均住宿費和平均雜費之和在特定的區間[1000，2 000]以及[3 000，5 000]內。根據上述c1約束，審計員應該審計那些平均花費不在上述區間的部門的報銷記錄。類似c1的聚合代數約束很難通過先驗知識獲得，這是因為這些聚合代數約束涉及兩列聚合運算結果（c1中為住宿費和雜費的聚合運算結果）之間的關系，該關系通常和數據分布高度相關。審計員需要采用數據驅動的方法從數據庫中自動發現聚合代數約束。

本文提出了一個從關系數據庫中高效地發現聚合代數約束的算法AAC-Hunter（Aggregation Algebraic Constraints Hunter）。在大數據時代，隨著數據體量越來越大，數據之間的約束關系變得越來越復雜。研究者們逐漸從以專家經驗為主的約束發現，轉向以數據驅動為主的約束發現，提出了一系列從數據庫中自動發現不同類型的約束關系的技術，以及根據約束維護數據一致性的技術，如：函數約束［1-4］、條件函數約束［5-8］、否定約束［9-12］、模式約束［13-14］、唯一約束［15］、代數約束［16］和時效規則［17-18］。然而，本文是第一項研究如何自動發現聚合代數約束的工作。AAC-Hunter 分兩步生成聚合代數約束：第一步，AAC-Hunter 根據數據模式信息，生成由全體候選聚合代數約束組成的候選集合。候選聚合代數約束中參與聚合運算的兩列可以來自同一張數據表，也可以來自不同的數據表。如果兩列來自不同的數據表，AAC-Hunter 自動決定兩張數據表的連接方法。示例聚合代數約束c1對應的候選聚合代數約束為(Avg(住宿費)+Avg(雜費))GroupBy(部門)。第二步，AAC-Hunter 為每條候選聚合代數約束計算一個值域集合，使該值域集合覆蓋數據庫中的大多數記錄，并將該候選聚合代數約束與計算出的值域集合輸出為最終的聚合代數約束 。AAC-Hunter 為c1計 算 出 的 值 域 空 間 為[1000，2 000]∪[3 000，5 000]。

從海量數據庫中自動發現聚合代數約束存在兩方面的性能挑戰：1）全體候選聚合代數約束組成的候選集合的規模巨大，難以在有限的時間內處理該候選集合中的每一條候選聚合代數約束；2）計算候選聚合代數約束的值域集合涉及表連接、聚合運算等耗時的數據庫操作，代價高昂。AAC-Hunter提出了一系列優化技術克服了上述兩個挑戰。本文的核心貢獻如下：

1）提出并形式化了一種新的數據庫模糊約束——聚合代數約束（第2.1節）。

2）提出了一個從數據庫中自動發現聚合代數約束的算法AAC-Hunter（第2.2節）。該算法采用一組啟發式規則減小候選聚合代數約束集合的規模（第3 章），并提出了兩項優化技術加速候選聚合代數約束值域集合的計算（第4章）。

3）在TPC-H 數據集和European Soccer 數據集上與基線算法的性能對比實驗驗證了所提出優化技術的有效性（第5章）。

1 相關工作

與本文相關的工作歸于基于數據驅動的約束發現。依據發現的約束關系的不同，相關工作分為：函數約束發現［1-8］、否定約束發現［9-12］、復雜模式約束發現［13-14］、唯一性約束發現［15］、簡單代數約束發現［16］和時效規則［17-18］。這些已有工作與本文工作的區別在于發現的約束關系不同。已有工作專注于發現數據庫中記錄之間或者列之間的各種約束關系，而本文工作研究的是兩列聚合運算結果之間的代數約束關系而非直接作用于數據庫兩列之間的代數約束關系。進一步，本文研究的聚合代數約束的候選集合在規模上也比現有工作研究的約束候選集大很多，需要新的剪枝和優化技術來處理。

2 發現聚合代數約束

2.1 聚合代數約束

聚合代數約束如定義1所示。

定義1給定關系數據庫D，聚合代數約束是一個作用于D中部分記錄上的八元組：

其中：a1、a2是D中的兩個屬性字段，可以來自同一張數據表，也可以來自兩張不同的數據表；f1、f2是分別施加在屬性a1、a2上的聚合函數，本文考慮5 種聚合函數：Count、Sum、Avg、Max和Min；二元運算符⊕是f1(a1)和f2(a2)間的代數運算符，包括+、-、×和/；I=I1∪I2∪…∪Ik為f1(a1)⊕f2(a2)的值域集合，其中Ii∈I是一個實數閉區間[a，b]，且I中任意兩個區間Ii、Ij滿足Ii∩Ij=?；如果a1、a2來自不同數據表，配對規則p指定數據表間的連接條件；g是分組規則，語義上等同于SQL的Group By 語句，指定與聚合運算相關的分組字段列。定義1 形式化地表明聚合代數約束是a1、a2在條件p、g下，使用函數f1、f2進行⊕運算后產生的值域集合I約束。式（2）進一步表示聚合代數約束中各因子間的關系：

其中：若a1、a2來自同一張表r，則配對規則p為平凡規則（即不需要表連接），記為p=?r；若a1、a2分別來自兩張表r和s，配對規則p指定r和s的連接條件，即其中cols1與cols2分別為表r、s上的連接字段；分組規則g=d1，d2，…，dn指定分組字段列。圖1 描繪了式（2）的運算流程。

圖1 聚合代數約束運算流程Fig.1 Calculation flow of aggregation algebraic constraint

為了更好地解釋聚合代數約束的含義，此處使用引言中的約束c1和另一個例子作進一步解釋。關系數據庫D1中存在報銷表（員工，部門，交通費，住宿費，雜費），使用定義1 中的符號規范表示約束c1，各元素如下所示：a1=住宿費，a2=雜費，f1=f2=Avg，p=?報銷表，g=部門，⊕為+（即加法運算），I=[1000，2 000]∪[3 000，5 000]。聚合代數約束c1表示了各部門報銷記錄中平均住宿費和平均雜費的和所符合一定的值域集合。關系數據庫D2儲存了某工廠檢驗生產工件的記錄，存在工件表（工件號，生產批次，倉儲位置）和檢驗表（工件號，外徑，內徑），一條聚合代數約束c2的元素如下所示：a1=外徑，a2=內徑，f1=f2=Avg，p=工件表?工件號=工件號檢驗表，g=生產批次，⊕為/（即除法運算），I=[3.123，3.127]。聚合代數約束c2描述了這個工廠生產的不同批次工件，各批次平均外徑和平均內徑的比值滿足一定的值域集合限制。由c1、c2可知，聚合代數約束描述了數據記錄根據某個屬性分組后，含統計特征的聚合代數運算結果具有一定的值域限制。

2.2 AAC-Hunter算法概述

AAC-Hunter分兩步從數據庫中發現聚合代數約束：

1）產生候選聚合代數約束集合C。根據數據模式信息生成所有形如c=(f1，a1，f2，a2，p，g，⊕)的候選聚合代數約束。全體候選聚合代數約束c組成集合C。

2）使用直方圖技術，為C中的每一個候選聚合代數約束c計算值域集合I，并輸出(c，I)作為發現的聚合代數約束。

上述算法簡單、易實現，但兩個原因使該算法無法應用于稍大規模的數據庫：1）對于稍復雜的數據庫，算法第一步將會產生海量規模的候選聚合代數約束集合，無法在有限的時間內處理該集合；2）計算I需要進行表連接和聚合運算操作，這些操作都非常耗時。本文在第3 章和第4 章引入一系列啟發式優化技術，降低處理代價，提升AAC-Hunter算法的伸縮性。

3 產生候選聚合代數約束

AAC-Hunter 算法的第一步是產生候選聚合代數約束集合C。該步驟進一步分為3 個子步驟：1）產生配對規則；2）產生分組規則和3）產生包含聚合運算的代數表達式。AACHunter 在每一個子步驟中引入一些啟發式剪枝規則，降低C的規模，本章詳細介紹這些實現細節。

3.1 產生配對規則

AAC-Hunter 首先產生配對規則p，組成集合P。由定義1，若a1、a2分別來自不同的數據表r和s，則AAC-Hunter 需要產生配對規則p指定表連接的方法。本文考慮兩種類型的表連接：1）若r、s之間存在外鍵約束，則按照外鍵約束連接兩個表；2）若r、s之間不存在外鍵約束，則AAC-Hunter 將在r、s中找到類外鍵約束的組合字段對(cols1，cols2)，并通過該組合字段對連接兩表。第一種類型的表連接比較簡單，本節詳細介紹如何產生第二種類型的表連接。

對包含a1和a2的表對(r，s)，AAC-Hunter在表對(r，s)中尋找所有可以連接的組合字段對(cols1，cols2)，其中cols1?r，cols2?s，滿足cols1和cols2長度一致（即，兩個組合字段cols1和cols2包含相同數目的字段）且cols1和cols2組合字段中對應位置的字段具有相同的數據類型。為了更有目的性地尋找這種組合字段對，可以參考數據庫中定義的索引字段，這些添加了索引的字段往往會被頻繁查詢且更加重要。這一步在最壞情況下將產生平方級別數量的組合字段對，為降低計算代價，AAC-Hunter引入以下兩條剪枝規則：

1）排除兩表均僅含有少量記錄的配對規則。這樣的配對規則無法通過后續計算分析得到有意義的值域集合。

2）排除由自增字段、NULL 值過多的字段組成類外鍵約束的配對規則。經驗表明這些字段或者與數據庫設計相關（即自增字段），或者與數據缺失相關（即NULL 值過多的字段）。這些字段并不存儲具有審計價值的數據，不是理想的連接字段。

3.2 產生分組規則

產生配對規則p之后，AAC-Hunter 接著生成分組規則集合G。該集合中的每個分組規則g由一個字段序列d1，d2，…，dn構成。AAC-Hunter 只考慮將具有類別屬性的字段（即，該字段只存儲有限數量的離散值，如部門字段）加入g。

對于配對規則p，假定執行連接運算r?s后結果表含有m個類別字段h1，h2，…，hm，若從中選擇i個字段（0 ＜i≤m）組成分組規則，此時產生Ci m種組合方式作為分組規則。這種樸素的方法將產生總計=2m-1 個符合條件的分組規則。顯而易見，分組規則的產生數目隨m增大而難以接受。AAC-Hunter使用以下方法來限制分組規則集合的規模：

1）引入分組序列長度最大值的超參數W以避免分組規則數過分增長。此步驟中，分組規則全集的數目至多為|G|=

2）分組規則中排除自增字段、NULL值過多的字段。

3）分組規則排除存在唯一性約束的字段。

4）分組規則排除由事實唯一字段（即，值幾乎各不相同的字段）組成的規則。

3.3 產生代數表達式

本節構造形如fi(ai)⊕fj(aj)的代數表達式。在配對規則p描述的連接運算結果中，AAC-Hunter 首先尋找可進行代數運算的字段作為ai，接著生成與ai的數據類型相兼容的聚合函數fi。本文考慮如下兩條類型兼容規則：1）對日期類型的ai，其兼容的聚合函數為Max、Min 和Count；2）對數值類型的ai，其兼容的聚合函數為Count、Sum、Avg、Max和Min。

對于按照上述過程產生的fi(ai)，枚舉二元組(fi(ai)，fj(aj))，并選取語義正確的⊕產生代數表達式fi(ai)⊕fj(aj)。在選取⊕時，AAC-Hunter 考慮如下語義約束：1）日期與日期之間僅能做減法運算；2）日期和整數型數據可以做加減法運算；3）Count函數無需明確屬性字段且只做乘法運算或者除法運算。作為特例，枚舉僅含單個計算屬性的情況形成代數表達式fi(ai)。

假定配對規則p產生的結果表中有l個字段可作為ai，則上述枚舉方案至多產生個代數表達式。AACHunter引入剪枝規則以減小代數表達式空間大小：

1）排除主鍵字段、自增字段、外鍵字段，以及配對規則p、分組規則g中涉及的字段。

2）排除分組規則和代數表達式相同，但配對規則不同的冗余的候選聚合代數約束。對于包含相同分組規則g=d1，d2，…，dn以及相同代數表達式fi(ai)⊕fj(aj)的多個候選聚合代數約束，AAC-Hunter 保留包含平凡配對規則p=?r的候選聚合代數約束，排除包含非平凡配對規則p=r?s的候選聚合代數約束。

4 產生候選聚合代數約束的值域集合

本章介紹如何產生候選聚合代數約束的值域集合I。AAC-Hunter 采用中間結果復用和消除平凡候選聚合代數約束兩項技術來加速處理候選聚合代數約束中的代數表達式計算，計算流程和加速技術的應用如圖2 所示。本章首先介紹這兩項技術，然后介紹如何從代數表達式的結果生成I。

圖2 計算流程與加速技術示意圖Fig.2 Schematic diagram of calculation process and acceleration techniques

4.1 復用中間結果

從前文論述中可以推知候選聚合代數約束集合C中大量候選聚合代數約束存在公共子操作。例如，如果兩條候選聚合代數約束中a1和a2都來自相同表對(r，s) 并進行運算，那么該連接運算就是這兩條候選聚合代數約束的公共子操作。類似地，如果兩條候選聚合代數約束包含相同的分組規則，那么分組操作就是公共子操作。為加速計算候選聚合代數約束中的代數表達式，AAC-Hunter 將候選聚合代數約束分類，并從每個分類中抽取公共連接和公共分組兩類公共子操作。對于公共子操作，AAC-Hunter 只計算一次，然后反復重用這些公共操作的結果，快速計算每條候選聚合代數約束的代數表達式。

AAC-Hunter 按照如下步驟對所有候選聚合代數約束進行歸類：1）將使用相同配對規則pi的候選約束歸類，記作2）將使用相同分組規則gj的候選約束歸類，記作；3）分析候選約束組，收集涉及到的所有分類字段和計算屬性，分別記作。歸類效果如圖3所示。

圖3 基于歸類的中間結果復用示意圖Fig.3 Reusing intermediate results based on classification

AAC-Hunter 采用的中間結果復用技術可以極大地降低計算代數表達式的成本。分析如下，不采用中間結果復用的計算總成本上限為：

其中：n為表的數目，m為連接結果表平均的分類字段數目，l為連接結果表平均的計算屬性數目，k1為配對規則描述的連接計算成本系數，k2為分組運算和代數表達式的計算成本系數，kp為產生配對規則數量相關的系數，W為限制分組規則序列長度的超參數。復用中間結果之后，總成本上限降為：

顯而易見，中間結果復用后計算成本得到大幅降低。

4.2 消除平凡候選聚合代數約束

生成聚合代數約束的最終目的是為審計應用服務，因此，生成的聚合代數約束必須具有代表性，即覆蓋了數據庫中絕大多數記錄；然而，有的候選聚合代數約束中配對規則描述的連接條件過于苛刻，以至于只有很少的記錄才能進入連接結果，無法覆蓋大多數記錄。類似地，有的候選聚合代數約束中分組規則的字段序列選擇不合適，使得結果集或者僅包含少數幾個分組且每個分組包含大量記錄，或者產生大量分組，但每個分組只有個別記錄，從而使結果集失去了統計意義。

本文稱至少滿足上述兩個條件（配對規則不合適、分組規則不合適）之一的候選聚合代數約束為平凡候選約束。AACHunter引入啟發式規則來跳過這些平凡候選約束的計算。

對于配對規則pi，若發現連接運算的結果記錄數較少，或遠低于參與連接的兩表記錄數，則意味著pi不是一條合適的配對規則。算法將終止接下來的計算，并從剩余候選約束中剔除所有候選約束組。如圖4（a）所示，假若配對規則p1不合適，則與其相關的候選約束組中所有候選約束均不再繼續計算。

對于分組規則gj而言，檢驗分組字段組合值的占比，僅計算占比滿足以下公式的分組規則：

1.2.1 發病規律調查 2015～2017年在試驗地對1～3年生青楊苗木的病害發病規律進行系統調查。采取標準地調查和線路調查2種方法，每年6月中旬開始，根據青楊病害歷年發生情況、扦插密度、樹齡、地形地貌、坡向、交通和管理等條件確定7個固定標準地，每個標準地選有代表性的青楊苗木15株，每株樹固定調查3～5個枝條，50～100片葉，每5d觀察1次病害發生情況，做好記錄。線路調查每10d進行1次，根據目測情況，每點調查20株，每株樹調查3～5個枝條，50～100片葉，借助80倍解剖鏡觀察葉片病斑發生情況。

其中：pi=r?s為對應配對規則的連接結果表，α為大于0 的參數，β為表示分組內最大記錄數量的參數。

若比值不滿足式（5）的要求，則意味著分組規則的組內記錄太多，或者分組字段序列的值有事實唯一的特性。若檢驗出分組規則gj無效，則意味著所有包含該分組序列的分組規則也都是無效的，那么將包含這些分組規則的平凡約束也一并剔除。如圖4（b）所示，假若分組規則g2失當，同時分組規則g3、g5與其共享相同的分組字段，那么它們對應的所有候選約束均被消除。

上述流程以一次計算成本為代價實現對大量平凡候選聚合代數約束的排除，這極大地彌補了發現候選約束階段帶來的計算空間爆炸的缺陷，減小與候選約束數量相關的成本：

其中：q為數據集實際存在的連接關系數量，且q≤kpn；u為代數表達式組的執行次數，一般u?；k3表示檢驗每個分組規則字段組合值占比的平均成本，且k3?k2；v表示查詢分組規則字段占比的次數，顯然v≥u。

圖4 消除平凡候選聚合代數約束示意圖Fig.4 Schematic diagram of eliminating trivial candidate AACs

4.3 生成有效值域集合

完成候選約束的代數表達式計算之后，AAC-Hunter 對結果進行離群值分析，得到正常和異常的值域集合。聚合代數約束作用于大多數記錄（指接下來被認定為是正常的記錄）而非全部記錄的模糊約束特性在此得以體現。

AAC-Hunter 使用時間復雜度為O(n)的直方圖法分析代數表達式的結果，將正常值域集合作為候選聚合代數約束的值域集合I。理想情況下，數據應是完全無錯的，所形成的約束值域集合應當是代數表達式結果的全域；然而，即便通過合法渠道進行數據持久化，也會產生異常數據（如表模式變更、實際業務的復雜性原因等），此時約束的值域集合應當剔除異常的部分，保留有效的大多數的部分。如圖5 所示，AACHunter 統計數值出現的頻度，按分布情況設定圖中橫線所示的閾值（閾值t=Rows(results) ×φ，超參數φ為留取比例），頻數大于閾值的區間被認定為有效區間，其他區間為無效區間，體現適用大多數而非全部記錄的模糊約束的性質。AACHunter 判定圖中結果序列的值域為I=[11，30]∪[35，36]。至此，AAC-Hunter完成發現一條聚合代數約束的流程。

圖5 基于直方圖的運算結果分析Fig.5 Histogram analysis for calculation results

僅從數據角度看來，AAC-Hunter 所發現的聚合代數約束由數據驅動產生，具有模糊約束的特征（即僅約束數據庫中的大多數而非全部記錄），通常難以使用專家知識構造，是準確有效的；然而，并非任意聚合代數約束都能成為滿足現實業務邏輯的審計規則，其原因在于，算法既無法通過降維后的數據還原實際業務的場景，又無法準確判別聚合代數約束是否能夠作為審計規則使用。因此，在程序結束后，審計員可以使用領域知識人工篩選有意義的聚合代數約束，并對值域結果做調整，使之成為審計規則。若認為圖5 柱形圖右側柱形區間[35，36]有異常的嫌疑，則可以在此程序結果上作進一步調整。

5 實驗

本文用Python 和SQLite 實現了AAC-Hunter 算法。本章介紹實驗結果。實驗在CPU 為AMD Ryzen 5 1400、內存為8 GB 的工作站上進行。實驗采用TPC-H 數據集（http：//www.tpc.org/tpch）和European Soccer 數據集（https：//www.kaggle.com/hugomathien/soccer），驗證AAC-Hunter的各種優化技術。

5.1 實驗設計與數據集

實驗流程如下：首先加載數據庫定義，然后產生候選聚合代數約束，最后產生候選聚合代數約束值域集合。根據經驗設計如下的超參數：實驗剪枝記錄數不超過200 條的表（認為記錄數少于200 條的表無發現聚合代數約束的價值），分組規則字段列長度上限參數W設定為3（即1條配對規則至多產生7 條分組規則），字段NULL 值比率需低于5%。若執行連接運算后表記錄數低于100 條或低于原表記錄數90%，認為該連接運算涉及的約束是平凡候選聚合代數約束的，則放棄對應配對規則。若檢查分組規則時發現組內平均記錄數低于2 條或大于100 條，認為該分組運算涉及的約束是平凡候選聚合代數約束，則放棄該分組規則。

鑒于AAC-Hunter 算法不言而喻的正確性（即，算法所發現的聚合代數約束對于給定數據一定是正確的，但無法判別在現實業務場景下的正確性），實驗關注AAC-Hunter 各種優化技術的實際效果，并不考慮所發現約束的現實意義。實驗在TPC-H、European Soccer 兩組廣泛使用的數據集上評估效果。TPC-H 是一種用于評估數據庫系統決策支持能力的數據集和執行標準，提供了商業銷售場景的表模式和數據，廣泛運用于數據庫系統的測試。鑒于AAC-Hunter 對表模式敏感，對記錄數量并不敏感（由記錄數量引入的復雜性本質上是對數據庫系統的性能校驗而非對AAC-Hunter 的優化技術效果校驗），實驗使用0.01的規模因子產生數據，整個數據集共計12個離散型分類字段。European Soccer 是一種收集于電子游戲的數據集，記錄了歐洲國家足球賽事、隊伍、球員等詳細信息，數據庫文件大小為300 MB。它包含了隊伍特征和球員屬性兩張寬表（具有較多數值類型字段），以及五張普通表（具有少量文本和數值類型字段），其中球員屬性表的記錄數多達18萬條，整個數據集共計20個離散型分類字段。

5.2 評估產生候選聚合代數約束效果

實驗統計了各數據集產生候選約束的效果。結果如表1所示，其中PR_TBL 表示產生配對規則階段剪枝兩表均僅含有少量記錄的配對規則，PR_INC、PR_NUL分別表示產生配對規則階段剪枝由自增字段、NULL值過多的字段組成類外鍵約束的配對規則，GR_INC、GR_NUL 分別表示產生分組規則階段剪枝由自增字段、NULL 值過多字段組成的分組規則，GR_IDX 表示產生分組規則階段剪枝由唯一性約束的字段組成的分組規則，GR_ATTR 表示剪枝分組字段由事實唯一字段組成的分組規則。OP_FAKE 表示代數表達式無效的剪枝，OP_RE 表示冗余候選聚合代數約束的剪枝。從表1 可以看出，一條候選約束可命中多條剪枝規則，剪枝規則間效果差異巨大，這與數據集特征密切相關。

表1 不同剪枝規則效果Tab.1 Effect for different pruning rules

各階段剪枝規則產生效果對比如表2 所示。在不剪枝時樸素的枚舉算法生成了數量龐大的結果，使用剪枝規則時大幅縮小了候選約束集合規模。在表2 中，剪枝后的分組規則數比配對規則數量更少，是由部分配對規則無法產生有效分組規則導致的。由表可知，即便European Soccer 數據集具有更多的列，但是其列大多數具有唯一性約束或列值具有事實唯一的特征，因此剪枝后的約束數量并未多于TPC-H 數據集的數量。此外，分組規則對配對規則的擴張并不明顯，但候選約束對分組規則的擴張十分顯著，如含有寬表的European Soccer 數據集枚舉代數表達式時產生了更多倍數的結果，使用剪枝規則可以收束各階段產生規則的放大效應。

表2 各階段產生候選約束結果數量對比Tab.2 Result number comparison for candidate constraint production at different stages

5.3 評估產生候選聚合代數約束值域集合效果

在第3 章介紹的所有剪枝規則產生候選聚合代數約束集合的基礎上，實驗對比了不使用任何優化策略（簡記為baseline）、僅復用中間結果（簡記為RE，4.1 節）以及同時復用中間結果和消除平凡候選聚合代數約束（簡記為RE+EL，4.1節和4.2節）三種執行方案的效果。

各方案運行耗時結果如表3 所示。可以直觀地看出，AAC-Hunter 算法設計的方案大幅提高了程序的執行速度，RE+EL 方案相對于baseline 方案在TPC-H 和European Soccer數據集上分別減小了95.68%和99.94%的約束發現空間，縮短了96.58%和92.51%的運行時間。通過baseline 和RE 方案實驗結果的對比，RE方案明確可以在不改變結果數量的前提下提升值域集合計算的效率，這符合復用中間結果技術的消除公共子操作效果。

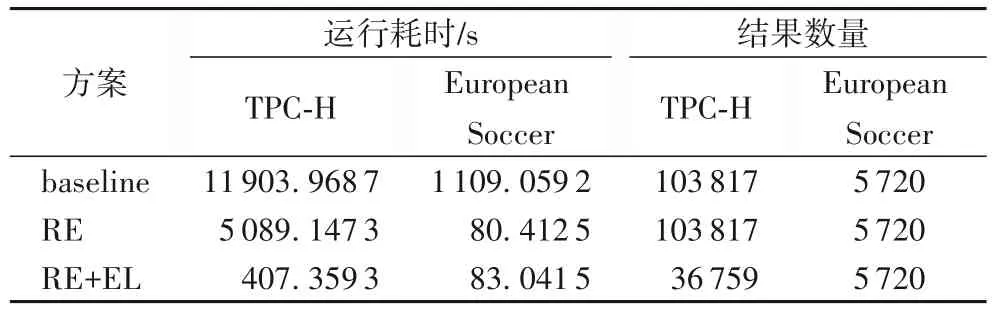
表3 不同執行方案的運行耗時、結果數量對比Tab.3 Running time and result number comparison of different execution schemes

值得一提的是，表3 中European Soccer 數據集中僅使用RE 方案卻比使用RE+EL 復合方案略微高效，是由于該數據集計算約束值域集合的過程并未受益于可能減少結果數的RE+EL 方案（表3 中RE+EL 方案、RE 方案的相同結果數說明了這一點），這符合式（6）所表達的含義。對于消除平凡候選聚合代數約束技術而言，既會因為檢查規則有效性而進行額外計算，又可能通過消除平凡候選約束間接減少更為耗時的值域集合計算，通常收益遠大于代價；然而即便應用消除平凡候選聚合代數約束技術未有收獲，從結果可以看出，其代價并非難以接受。

6 結語

本文提出了AAC-Hunter，一個從關系數據庫中高效地發現聚合代數約束的算法。AAC-Hunter 采用一系列啟發式規則減小了候選聚合代數約束集合的大小，并優化了候選聚合代數約束的值域集合計算。AAC-Hunter 與基線算法的對比實驗表明，提出的優化技術顯著縮短了發現聚合代數約束所需的計算時間。