基于粗糙集理論的不完備數據分析方法的混合信息系統填補算法

，2*

（1.成都信息工程大學軟件工程學院，成都 610225；2.西南交通大學信息科學與技術學院，成都 611756；3.成都大學計算機學院，成都 610106）

0 引言

近年來，由于數據來源廣泛且復雜、人類認知的局限性，以及硬件故障、手工錄入錯誤、編程錯誤等，導致數據產生一定比例的缺失，使得知識的有效獲取變得愈來愈困難；如何科學地處理缺失數據、提高數據質量是當下數據挖掘領域的研究難點之一。現實生活中描述數據的形式多種多樣，缺失機制也各不相同，使得基于粗糙集理論的不完備數據分析方法（ROUgh Set Theory based Incomplete Data Analysis Approach，ROUSTIDA）［1］無法滿足所有數據的需求。本文立足于混合信息系統，即包含離散型（如整型、字符串型、枚舉型）、連續型（如浮點數表達）、缺失型屬性的信息系統，研究分析發現，混合屬性將嚴重影響ROUSTIDA 對數據之間相似性的度量，從而使得填充效果不理想。為了解決該問題，本文在定義混合距離的基礎上結合近鄰思想與等價類劃分原則，提出了一種基于粗糙集理論的混合信息系統缺失值填補方法（Rough Set theory based Hybrid Information System for Missing data Imputation Approach，RSHISMIA）。本文的主要工作包括5 個方面：

1）使用了混合距離量化樣本間相似度。

2）定義了混合距離矩陣，剔除不具備填補能力的數據。

3）采用決策屬性等價類劃分思想，有效地改善了可能存在的決策屬性沖突問題。

4）引入最近鄰思想，減輕噪聲數據的影響。

5）使用UCI 數據集與4 種填補算法進行對比實驗，結果表明RSHISMIA 在查準率和查全率方面顯著優于ROUSTIDA，填補后的分類準確率相較4 種對比算法也有所提高。

1 相關工作

自1970 年來，國內外陸續提出的缺失數據的處理方法大致可以分為以下3類。

1）直接刪除法：簡單地將存在缺失屬性值的實例刪除，從而得到完備的信息系統。但當信息表中信息較少、存在缺失屬性值的實例較多時，會嚴重影響信息系統中的信息量。

2）特殊值法：該途徑將缺失屬性值作為一種特殊的屬性值來處理，它不同于其他任何屬性值，從而不完備信息系統就成為完備信息系統。

3）填補法：按照特定方式對缺失數據進行估計，使用估計值替換缺失數據，從而得完備信息系統，該方法也是最常用的方式。

目前，對缺失值的填補包含基于機器學習算法和基于粗糙集理論等的方法。其中，基于機器學習算法的方法需要利用完備信息系統訓練模型，從而對缺失值進行預測，如一種基于支持向量機（Support Vector Machine，SVM）的缺失數據填補算法［2］，該方法使用支持向量回歸填補含有缺失信息的基因表達數據，通過正交化編碼輸入方案，把缺失數據映射到更高維空間，從而填補缺失數據。Stekhoven 等［3］提出了基于隨機森林的數據填補（Random Forest Imputation，RFI）算法，該算法適用于類別型屬性較多且樣本數量較小的數據集。Dixon［4］提出了K 近鄰填補（K Nearest Neighbor Imputation，KNNI）算法，該算法首先在數據集中找到與缺失數據樣本的k個最相似樣例，然后利用這k個樣例相應的屬性值對缺失值進行填補。Ranjbar等［5］通過使用未知對象的估算評級來提高基于矩陣分解（Matrix Factorization，MF）算法的性能，該算法可以改善數據稀疏性和過擬合問題。而由波蘭學者Pawlak［6］提出的粗糙集理論及其擴展模型為不完備信息系統的處理奠定了良好的基礎。該理論能夠在保持信息系統分類能力不變的前提下，無需提供問題所需處理的數據集合之外的任何先驗信息。在此基礎上，最具代表性的離散型數據填補算法是Zhu 等［7］提出的基于容差關系的ROUSTIDA。針對該算法所存在的缺陷，許多學者進行了廣泛的研究。蔣亞軍等［8］在模糊相似關系的基礎上，針對具有連續屬性的不完備信息系統提出了Rough 集的擴展模型，在模糊關系的基礎上給出了不完備信息表的上近似和下近似的定義；利用基于歐氏距離的貼近度法計算模糊相似度，構造相似矩陣，實現了對論域的劃分。朱小飛等［9］根據擴充后的量化容差關系提出VTRIDA（Valued Tolerance Relation based Incomplete Data Analysis）算法，實現一次直接補齊缺失值，減少了計算開銷。劉文軍［10］針對不同的屬性類型給出了條件屬性相似度，就不同條件屬性類型的決策表給出了相應的補齊算法，并給出了τ相似度的概念，但該參數τ的選取沒有合適的方法。王國胤［11］提出了基于限制容差關系的擴展粗糙集模型，該模型結合了容差關系和非對稱關系的優缺點。霍忠誠等［12］根據極大相容塊中的元素之間具有最高的相似度的性質，提出了一種改進算法，提高了ROUSTIDA 對離散型不完備數據的填充能力。丁春榮等［13］提出了基于決策獨立原則的改進算法，有效地解決了原算法可能存在的噪聲問題。關瑩等［14］針對數據稀疏度大的信息系統提出了一種基于序數屬性相似度的不完備數據分析方法，該算法使用差值替代等值的方式改進擴充差異矩陣，改善了其他改進方法對序數屬性處理不準確的缺點。為了克服ROUSTIDA 在無差別對象屬性值發生沖突情況下無法對相同屬性進行補齊的缺陷，并改善VTRIDA 算法對容差關系不合理的量化定義，Bai等［15］提出了綜合量化容差關系和限制容差關系的數據填充方法VLTA（Valued and Limited Tolerance Algorithm）。Prieto-Cubides 等［16］結合了廣義非對稱相似度關系和廣義分辨矩陣，提出適合缺失率較大的填補（Agreements based on Rough Set Imputation，ARSI）算法，但是該算法僅能處理離散型數據。樊哲寧等［1］提出了一種針對具有關鍵屬性的重復數據的改進算法，考慮了目標屬性重復性的同時分析了關鍵屬性對填補效果的影響。然而上述研究基本是針對具有單一離散屬性或連續屬性的不確定系統進行的，無法處理具有離散屬性、連續屬性和缺失屬性的混合信息系統。因此，本文提出了一種基于粗糙集理論的混合信息系統缺失值填補方法RSHISMIA。

2 ROUSTIDA

2.1 基本定義

ROUSTIDA 采用粗糙集理論實現不完備信息系統的缺失數據填補。該算法的基本思想是：缺失數據的填補應使具有缺失數據的對象與信息系統的其他相似對象的屬性值的差異盡可能保持一致，使填補前后屬性值之間的差異盡可能保持最小。

定義1信息系統S［7］。

S=論域U=｛x1，x2，…，xm｝是一組包含m個對象的非空有限集合。A是有限個屬性的非空有限集合，設有n個屬性，則表示為A=｛a1，a2，…，an｝，對每一個ak∈A，ak：U→是屬性ak的值域。其中，值域可能包含使用特殊符號“*”表示的數據缺失值，此時該信息系統記為不完備信息系統；且A可以進一步劃分為兩個不相交的子集合：條件屬性C和決策屬性D，滿足A=C∪D且C∪D=?，此時的信息系統稱為決策系統，其中D一般只包含一個屬性。

定義2擴充差異矩陣M［7］。

S=論域U={x1，x2，…，xm}，屬性集A=C∪D，條件屬性集C，決策屬性D，ak(xi)是樣本xi在屬性ak上的取值。Mij表示經過擴充的差異矩陣中第i行、第j列的元素，則擴充差異矩陣元素Mij定義為：

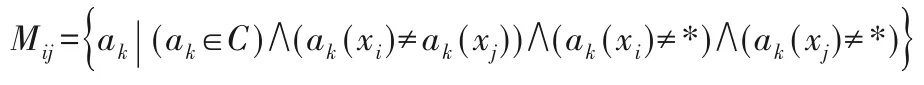
其中：i，j=1，2，…，m，k=1，2，…，n，m=|U|，n=|A|，*表示缺失數據。矩陣M中的元素為屬性的集合，且該矩陣為m×n的方陣。

定義3對象xi缺失屬性集MASi（Missing Attributes Set）。

對象xi缺失屬性集MASi是包含k(1 ≤k≤n)個屬性且滿足下列條件的有限集合：

定義4無差別對象集NSi。

對象xi無差別對象集是包含j(1 ≤j≤m)個對象且滿足如下條件的集合：

定義5缺失對象集MOS。

信息系統S缺失對象集MOS（Missing Objects Set）是滿足如下條件的集合：

2.2 算法描述

基于上述的定義，不完備數據分析算法ROUSTIDA 描述如下：

算法1 ROUSTIDA。

根據上述算法描述可分析得到，ROUSTIDA 存在如下問題：

1）填補過程中未區分決策屬性D和條件屬性C，可能會導致填補后的信息系統出現決策沖突現象，即兩個樣本的條件屬性值相同而決策（分類）屬性值不同。

2）當對象xi的NSi=?，即沒有其他對象與xi相似時，無法填補xi的缺失數據；或當對象xi存在多個相似對象，且多個相似對象能夠給予填充的屬性值不一致時，也無法進行填充。

3）該算法僅考慮對象間的相似關系，忽略了對象是否具備填補能力的判斷，可能導致NSi中部分相似對象實際上不能對缺失數據進行填補。

3 RSHISMIA

根據上述原算法ROUSTIDA 存在的問題，本文提出了一種改進的針對不完備混合信息系統的缺失數據填補方法（RSHISMIA）。

3.1 距離矩陣

為了改進算法，引入Zeng等［17］給出的如下定義6。

定義6混合信息系統HIS。

HIS=C∩D=?，U為論域，Vd=｛d1，d2，…，dm｝為決策屬性的值域，C=Cr∪Cb∪Cc，Cr是數值屬性集合，Cb是布爾屬性集合，Cc是類別屬性集合，且Cr∩Cb=?，Cr∩Cc=?，Cb∩Cc=?。若包含使用特殊符號“*”所表示的缺失數據時，該信息系統記為不完備混合信息系統。

如表1為一個不完備混合信息系統。其中，D表示決策屬性，c1、c2、c3、c4為條件屬性，“*”表示缺失數據，“Temperature”為數值屬性，“Degree of headache”“Degree of muscle pain”為類別屬性，在預處理過程中需要對具有序數關系的類別屬性使用Géron［18］給出的One-hot Encoder（獨熱編碼）進行轉換，對不具有序數關系的類別屬性使用Label Encoder（標簽編碼）轉換。“Cough”為布爾屬性，僅包含“yes”和“no”兩個取值，不具備序數和大小關系。此外，布爾屬性遵循Bernoulli分布，而類別屬性遵循離散概率分布，因此，需要對不同類型的屬性進行相應的處理。目前，為了量化混合信息系統對象間的相似度，He等［19］給出了樣本間的混合距離（定義7）和針對屬性類型不同而給出的布爾屬性距離（定義8）。為了更合理量化不完備混合信息系統中樣本的距離，在上述工作的基礎上，修改定義了類別屬性（定義9）和數值屬性（定義10）的距離計算方式，并給出了距離矩陣（定義11）。

表1 不完備混合信息系統Tab.1 Incomplete hybrid information system

定義7混合距離HD。

HIS=U=｛x1，x2，…，xm｝，?xi，xj∈U，?c∈C，c(xi)、c(xj)分別表示樣本xi和xj在條件屬性c上的取值，樣本xi和xj之間距離定義如下：

其中d(c(xi)，c(xj))的定義如下：

定義8布爾屬性距離db。

HIS=U=｛x1，x2，…，xm｝，?xi，xj∈U，?c∈C，c是布爾屬性，c(xi)、c(xj)分別表示樣本xi和xj在條件屬性c上的取值，樣本xi和xj之間距離定義如下：

定義9類別屬性距離dm。

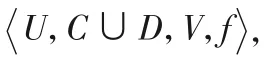
HIS=U=｛x1，x2，…，xm｝，?xi，xj∈U，?c∈C，c是類比屬性，c(xi)、c(xj)分別表示樣本xi和xj在條件屬性c上的取值，樣本xi和xj之間距離定義如下：

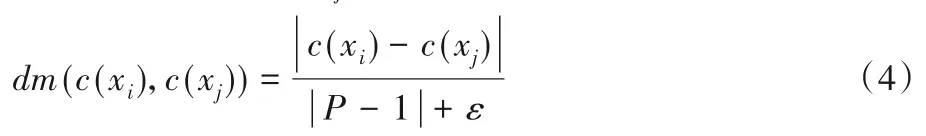
其中：P為類別屬性c的取值個數；ε取值為10-5，防止分母為0。此外若使用One-hot Encoder，|c(xi)-c(xj)|=

定義10數值屬性距離dr。

HIS=U=｛x1，x2，…，xm｝，?xi，xj∈U，?c∈C，c是數值屬性，c(xi)、c(xj)分別表示樣本xi和xj在條件屬性c上的取值，樣本xi和xj之間距離定義如下。

其中δr為數值屬性c的標準差，ε取值為10-5。

在缺失數據填補過程中，不僅需要使用混合距離度量對象之間的相似關系，還需要將它們可互相填補的能力納入考慮范圍之內。故本文在使用混合距離基礎上，還增加定義了距離矩陣DM。

定義11距離矩陣DM。

HIS=U=｛x1，x2，…，xm｝，條件屬性集C=｛c1，c2，…，cn-1｝，c(xi)是樣本xi在條件屬性c上的取值。距離矩陣DM的元素DMij（第i行第j列的元素）表示樣本xi和樣本xj的距離，其定義如下：

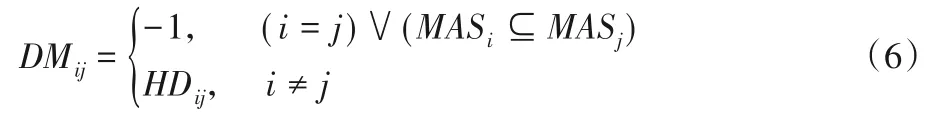
由于HDij取值為[0，+∞]，-1取值是合理的。

根據上述定義可得DM是一個非對稱的m×m方陣，其表征的對象相似度考慮了填補能力因素。特別是當對象xj不具備填補對象xi的能力時，不論二者的距離（相似程度）為多少，都將DMij定義為-1。

3.2 算法描述

根據上述定義，RSHISMIA 描述（算法2）如下。首先，依據等價類劃分思想，依據決策屬性值Vd=｛d1，d2，…，dm｝將不完備混合信息系統HIS劃分為子系統HIS1，HIS2，…，HISl，且滿足HIS=HIS1∪HIS2∪…∪HISl。對每個子系統HISk(k=1，2，…，l)進行缺失數據填補。最后將填補后的所有子系統HISk融合為一個混合信息系統，若仍存在缺失數據，則使用GRZYMALA-BUSSE 等［20］給出的 CMC（Condition Most Common）方法進行輔助填補，即對于類別屬性使用眾數填補，對于數值屬性使用平均值填補。

算法2 RSHISMIA。

3.3 實例分析

將RSHISMIA 與ROUSTIDA 的填充結果進行對比。一個不完備混合信息系統如表1 所示，通過RSHISMIA、ROUSTIDA 填補后的效果分別如表2、3 所示。ROUSTIDA 出現無法填補的條件屬性較多，填補效率低，且重新計算無差別矩陣時計算較復雜，同時還出現了x2與x3決策規則沖突的情況。決策規則沖突的原因是因為在補齊x2和x3時，選擇的補齊對象是從整個不完備決策表中去尋找無差別對象，在完成決策表的循環計算后條件屬性仍無法補齊，采用CMC 進行補齊從而導致決策規則沖突。文中所用的決策屬性等價類劃分思想由于分別考慮了同一決策子系統和不同決策子系統中最相似的對象對填補的不同影響，較好地避免了沖突。同時，在計算混合距離矩陣時，由于每次循環只需要計算該矩陣中值不為-1 的元素，所提RSHISMIA 較ROUSTIDA 的無差別矩陣的計算更為簡單。

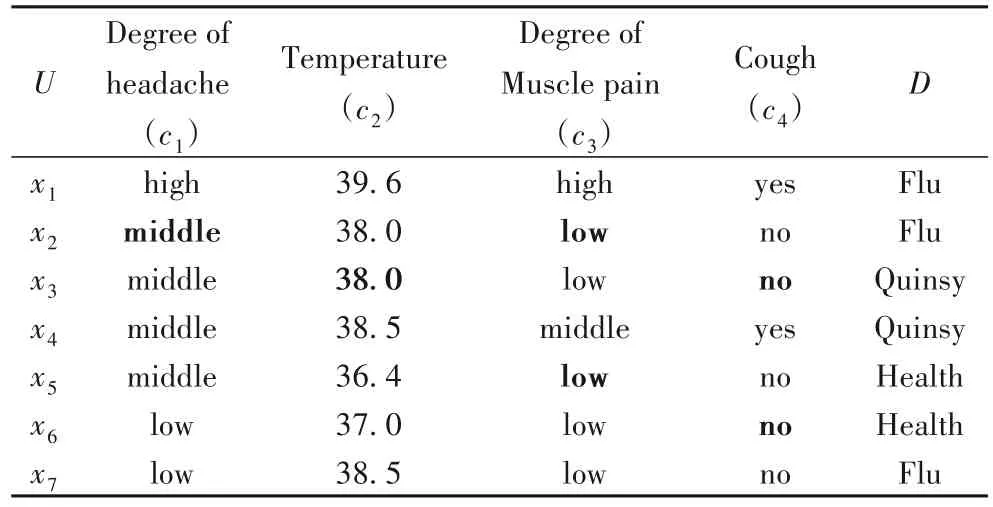
表2 ROUSTIDA填補結果Tab.2 Imputation results of ROUSTIDA

3.4 算法時空復雜度分析

算法2中，步驟3）～5）的復雜度主要取決于計算距離矩陣DM。假設論域被劃分為U=U1∪U2∪…∪Ul，分析可得，Ul所有對象兩兩相互比較，則需要比較|Ul|*|Ul|/2 次，并且任意兩個對象需要對所有條件屬性進行比較，比較次數為|C|。因此，DM矩陣計算的復雜度為O(|C||Ul|2)。步驟6）～16），計算復雜度主要取決于缺失數據的個數，為常數數量級。綜上，算法2填補過程的復雜度為O(|C|(|U1|2+|U2|2+…+|Ul|2)；由算法1 可得，使用ROUSTIDA 對整個論域空間建立擴充差異矩陣，所有對象相互比較，需要比較|U|(|U|-1)/2 次，并且任意兩個對象需要對所有屬性進行比較，比較次數為|A|，因此計算矩陣的復雜度為O(|A||U|2)。

此外，使用改進后的距離矩陣存儲空間由原本的O(|A||U|2)降低到O(|C|(|U1|2+|U2|2+…+|Ul|2)。對于|U|大于600 或|C|大于10 的數據集而言，空間復雜度降低效果較明顯。

4 實驗結果與分析

在本章中，使用ROUSTIDA 和本文提出的缺失數據填補算法RSHISMIA 以及目前較流行的缺失數據填補算法KNNI、MF、RFI 進行對比實驗。以下所有實驗均使用Windows 10 64 位操作系統，Intel i7-7500U CPU 2.7 GHz，8 GB RAM，Python 3.6進行編程。

4.1 評價標準

缺失數據的填補標準一般分為3 種：周志華［21］給出的查全率（Recall）用于評估填補能力和查準率（Precision）用于衡量填補的準確度，以及Dauwels 等［22］給出的歸一化均方根誤差（Normalized Root Mean Square Error，NRMSE）用于檢驗填補結果與真實值的差異度，具體公式定義如下：

其中：m表示數據集樣本個數；TP（True Positive）表示缺失數據填補正確個數；FP（False Positive）表示缺失數據填補錯誤個數；FN（False Negative）表示未填補的缺失數據個數；xi表示原始值，xi'表示填補值，xmax和xmin分別為最大值和最小值。

交叉驗證是一種用于測試模型預測新數據能力，預防過擬合或選擇偏差等問題，并提高模型泛化能力的統計方法。將數據集W劃分成k個大小相似的互斥子集，即W=W1∪W2∪…∪Wk，Wi∩Wj=?(i≠j)。每個子集Wi都從W中分層采樣得到，從而盡可能保持數據分布的一致性。然后，每次用k-1個子集的并集作為訓練集，余下的那個子集作為測試集，這樣就可獲得k組訓練/測試集，從而可進行k次訓練和測試，最終返回的是這k個測試結果的均值。顯然，k的取值很大程度上影響了交叉驗證法評估結果的穩定性和保真性，為強調這一點，通常交叉驗證法稱為“k折交叉驗證”，k最常用的是10。本文使用10 次交叉驗證可以減少與隨機抽樣相關的偏差。

4.2 數據集

本文在Dua等［23］給出的10個標準UCI數據集上驗證所提出的方法。其中，包含3個類別型數據集（Lymphography、SPECT、Balance Scale）；7 個混合型數據集（Acute Inflammations、Contraceptive、Heart、Liver、Zoo、German、Abalone）。下面從數據集大小和數據特點等方面分別介紹這10 個數據集（如表4 所示）。以下數據集均不存在缺失數據，數據集的樣本個數變化范圍為101～4177，屬性個數范圍為4～22。

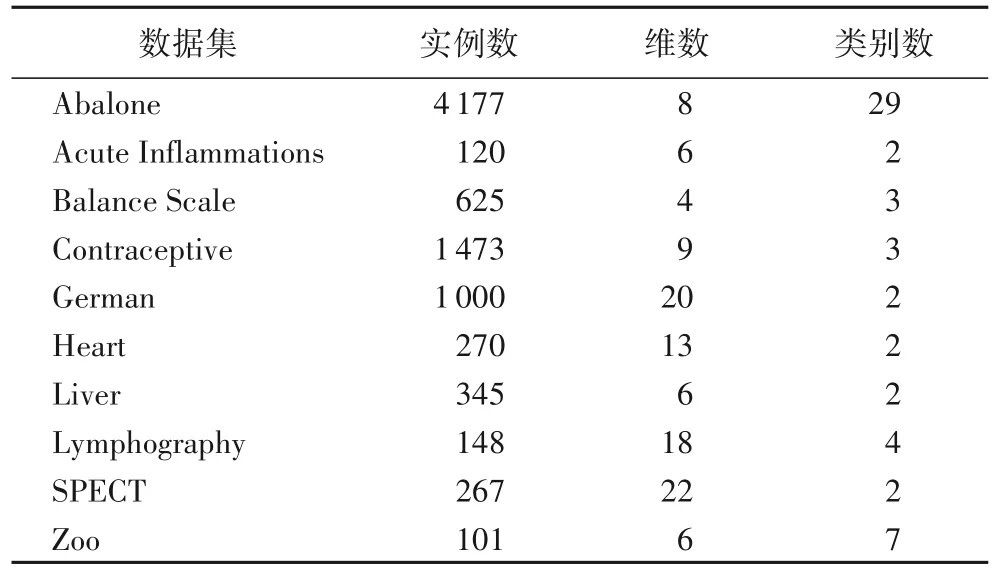
表4 數據集描述Tab.4 Dataset description

4.3 實驗設置

本節中描述了所完成的3 個實驗來驗證所提出的缺失數據填補算法RSHISMIA 的可行性和有效性。首先對數據集Abalone 使用Alexksander［24］提出的Rosetta 的Equal Frequency Scaler 函數對數據集中連續屬性數據進行離散化處理。上述數據集均不存在缺失數據，因此，本文采用Alfons［25］給出的R語言SimFrame 庫的隨機數據生成器確定缺失數據的位置，然后刪除相應的屬性值，生成不完整的信息系統。對條件屬性使用10 個不同的隨機數作為種子，隨機產生5%、10%、15%、20%、25%、30%比率（α）的缺失數據，分別得到6 × 10 × 10 個（6種缺失率，每種缺失率10次隨機缺失，10個數據集）不完備的信息系統。然后，使用RSHISMIA、ROUSTIDA、KNNI、MF和RFI 5種算法分別進行填補，最后將填補后得到的完整信息系統看作一個決策系統。使用Cortes等［26］提出的SVM算法進行10 次10 折交叉準確率驗證后取平均值。其中SVM 使用徑向基函數（Radial Basis Function，RBF）核函數，并使用Hsu等［27］提出的交叉驗證網格搜索尋找最優參數(C，Y)。此外，為防止樣本中不同特征數值大小相差較大影響分類器性能，采用Zheng 等［28］給出的標準化處理方式進行數據集處理。相關填補模型和分類模型參數設置如表5所示。

表5 相關填補和分類模型參數設置Tab.5 Parameter setting of related imputation and classification models

第1 個實驗是通過改變RSHISMIA 近鄰個數k的取值，判斷k取何值時算法的NRMSE 可以達到最優值。參考KNN 算法的k值選取，Lall 等［29］提出了一種可選擇的方式，即k=(m≥100)，這里m為樣本個數。由于數據集的特性不同，沒有關于最優k的先驗信息，所以k的最優值將根據所提RSHISMIA 的實驗結果來設定。這里k值取值范圍為1、3、5、10、15、20。

第2 個實驗，對RSHISMIA 和ROUSTIDA 進行查全率、查準率和NRMSE的比較。

第3個實驗，對RSHISMIA 和ROUSTIDA 無法填補的缺失數據使用CMC 方法輔助填補，并將輔助填補后得到的混合信息系統與KNNI、MF、RFI 等3 種算法分別填補后的混合信息系統使用SVM算法進行分類預測。

4.4 結果分析

實驗1 結果表明，對于樣本個數較小的混合型數據集（≤350）而言，k的取值為3 的NRMSE 較小。對于樣本個數較少的類別型數據集（≤350）而言，k的取值為10 較優。對于樣本個數較大的混合型和類別型數據集（≥350）而言，k取20 可以使得NRMSE 的值較小。此外，對于大部分數據集而言，NRMSE 不會隨著k波動太大，基本穩定不變。因此，綜合分析，本文選取k值為15作為后續對比實驗的基準。

實驗2 結果表明RSHISMIA 對10 個數據集的查全率均高于ROUSTIDA（見表6），平均提高了約81 個百分點，這是因為使用近鄰樣本，擴大了可用于填補的相似樣本的選擇范圍。依據數據集的不同，查準率（見表6）較ROUSTIDA 在所有缺失率情況下也有所提高，如數據集Acute Inflammations 平均提高了23個百分點，數據集Zoo平均提高了29個百分點，SPECT數據集平均提高了5 個百分點。此外，對于RSHISMIA，大部分數據集的NRMSE 相較ROUSTIDA（見表6）也有所減小，如數據集Liver 的NRMSE 減少了0.002～0.006，數據集Balance Scale 平均減小了約0.02。數據集Zoo 的NRMSE 減小了0.06～0.12。

實驗3結果為同一數據集在同一缺失比例下使用SVM 算法進行10 次十折交叉驗證分類準確率取平均后的結果（如圖1 所示）。可以觀察到，算法RSHISMIA 對數據集Lymphography、Heart、Liver、German 所有缺失率的情況下分類準確率都最高，分別為91.97%、89.22%、71.46%、79.81%。而數據集SPECT 和Zoo 在缺失率為10%～25%的情況下，填補算法RSHISMIA 的表現較好，最高分別達到了75.19%、97%，其次是KNNI，相差在1%～3%左右。此外，對于Balance Scale和Acute Inflammations、Contraceptive 這三個數據集而言，RSHISMIA 較大多數算法的表現都好，僅次于RFI。在缺失率為15%～25%時，RSHISMIA 在數據集Abalone 上效果僅次于KNNI，甚至在缺失率為30%時超過了KNNI達到最優，可以達到32.41%。

綜上，使用RSHISMIA 填補包含混合屬性的信息系統是有效可行的，更適合填補數據量小且缺失率高的混合信息系統，且對樣本量較大的混合填補效果也基本與最優算法持平。

表6 不同數據集不同缺失率的實驗結果Tab.6 Experimental results on different datasets with different missing rates

5 結語

針對傳統ROUSTIDA 無法有效處理包含不同屬性類型的混合信息系統，本文提出了RSHISMIA 填補算法。該算法既繼承了粗糙集理論的優點，對數據的先驗性要求不高，又通過對決策屬性進行等價類劃分，解決可能出現的決策規則沖突問題；定義不同屬性的距離公式度量樣本的相似度，得到比容差關系更適合作為尋找最相似對象基礎的混合距離；定義混合距離矩陣篩選更具填補能力的樣本；最后結合了近鄰的思想，擴大了待填補數據的相似對象的選擇范圍。實驗結果表明，本文提出的缺失數據填補算法RSHISMIA，在10個標準數據集上的查全率、查準率、NRMSE 相較ROUSTIDA 都取得了更好的性能指標，分類準確率較其他填補算法也有提升。

綜上，本文所提的RSHISMIA 可以合理有效地處理樣本量小、缺失率高的不完備混合信息系統，且處理結果具有客觀性，有一定的借鑒意義；但要求數據的決策屬性不存在缺失，具有一定的局限性。因此，未來需要對決策屬性存在缺失數據的填補方法進行研究。

圖1 不同算法在不同數據集上隨缺失率變化的分類準確率Fig.1 Classification accuracies of different algorithms with change of missing rate on different datasets