自動確定聚類中心的比較密度峰值聚類算法

，2*

（1.山東科技大學測繪科學與工程學院，山東青島 266590；2.山東省基礎地理信息與數字化技術重點實驗室（山東科技大學），山東青島 266590）

0 引言

隨著互聯網、社交網絡等技術的迅猛發展，數據源的多樣化使數據量呈現爆炸式的增長，如何在大規模數據集中進行有效的分析并挖掘背后的價值已經成為了眾多行業面臨的首要問題。聚類分析［1］作為一種重要的數據挖掘技術，能夠在無監督的條件下探索數據背后潛在的數據結構。依據聚類算法原理的不同，可將現有的聚類算法大致分為五類［2-3］：劃分聚類［4］、層次聚類［5］、密度聚類［6］、網格聚類［7］以及模型聚類［8］。k-means 算法［9］是著名的劃分聚類算法，具有操作簡單、效率高等優點，但需要預先指定聚類個數；基于密度的噪聲應用空間聚類（Density-Based Spatial Clustering of Application with Noise，DBSCAN）算法［10］對密度估計使用了索引結構，在處理大規模數據集時，有效地提高了聚類速度，但容易受鄰域半徑和閾值這兩個參數的影響；Ankerst 等［11］提出了OPTICS（Ordering Points To Identify the Clustering Structure）算法，該算法解決了DBSCAN 對輸入參數敏感的問題；Frey 等［12］提出了一種與k-means 同屬于劃分聚類的近鄰傳播（Affinity Propagation，AP）聚類算法，該算法不需要指定聚類個數，但所得的聚類個數受“preference”的影響。

2014 年6 月，Rodriguez 等［13］首次提出了密度峰值聚類（Density Peaks Clustering，DPC）算法。該算法簡單高效、無須迭代，能夠檢測任意形狀的類簇，且不需要提前設定類簇的數量，目前在圖像分割、醫學影像處理、社區發現［14-17］等領域具有潛在的應用價值。但該算法也存在缺陷：1）采用歐氏距離進行距離度量，無法正確反映復雜數據集的分布情況；2）對截斷距離異常敏感，微小的變化就會導致不同的聚類結果；3）在確定聚類中心時需要根據決策圖手動選擇聚類中心，效率低下。為了解決DPC存在的問題，Du等［18］將流形學習的測地距離引入距離度量中，很好地解決了包含有多流行結構的數據處理問題；Mehmood 等［19］引入熱擴散理論提出了一種從數據集中自動提取截斷距離的方法，解決了DPC 算法中參數難以確定的問題；吳斌等［20］將基尼系數引入提出了一種自適應截斷距離的方法，以獲得最優的截斷距離值；馬春來等［21］根據簇中心權值的變化趨勢來搜索“拐點”，并將“拐點”之前的點作為各簇中心，該算法避免了通過決策圖判斷簇中心的方法所帶來的誤差；丁志成等［22］利用KL（Kullback-Leibler）散度的差異性度量準則劃分聚類中心點和非聚類中心點，根據散度排序圖中的拐點實現對聚類中心的自動選取。

基于現有研究，本文設計了一種自動確定聚類中心的比較密度峰值聚類算法（Comparative density Peaks Clustering algorithm with Automatic determination of clustering center，ACPC）。ACPC根據決策圖中數據的分布特征，采用了基于統計分析的二維區間估計方法來自動地識別決策圖中聚類中心點。距離比較量主要集中對第二個假設的定量建模上，使聚類中心點在決策圖中更明顯地區別于非聚類中心點。實驗結果說明，新算法有較高的準確性且適應性更好。

1 經典DPC算法

密度峰值聚類算法是一種可以發現非凸簇類的新型聚類算法。其核心思想建立在對聚類中心點的兩個重要假設之上。

假設1 聚類中心的局部密度大于其周圍鄰近點的密度。

假設2 聚類中心與比其密度高的數據點的距離相對較遠。

根據這兩個設定，聚類中心應該是同時具備較大局部密度和較大相對距離。要確定數據集的聚類中心，對于每一個數據點，都需要計算兩個屬性：數據點i的局部密度pi和相對距離δi。令待聚類的數據集S={x1，x2，…，xn}，IS={1，2，…，n}為相應的指標集。

定義1局部密度pi（Cut-off kernel 和Gaussian kernel 兩種計算方式）。

Cut-off kernel：

其中函數：

式（1）中：i和j分別為第i個數據點、第j個數據點；rij=，rij為數據點xi和xj之間的歐氏距離；參數rc為截斷距離，其作為密度峰值聚類算法的唯一參數，實際起著距離閾值的作用。

Gaussian kernel：

式（1）為數據集規模較大時數據i的局部密度計算方式；當數據集的規模較小，為減小截斷距離的選擇對算法的影響，DPC 算法采用高斯核函數來估計數據i的局部密度，如式（3）所示。

定義2相對距離δi：

計算pi和δi之后，密度峰值聚類算法通過構造決策圖選擇pi和δi都較大的數據點作為聚類中心。

圖1（a）展示了原始數據點集的分布。圖1（b）為該數據集的決策圖，其包含每個數據點的局部密度pi和相對距離δi。從決策圖中可以容易發現，灰色圓形點和菱形點標記的數據點為聚類中心點，因為這兩個點同時具有較大的pi值和δi值。

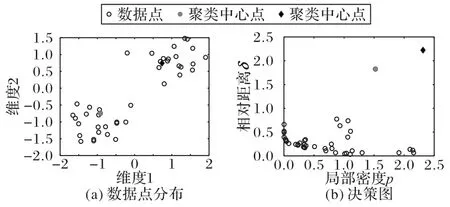
圖1 原始數據點分布和決策圖的實例Fig.1 Examples of original data point distribution and decision graph

在選定聚類中心后，密度峰值聚類算法按照密度從大到小的順序將剩余數據點依次歸入比它密度大且與其距離最近的數據點的類簇，僅一步就可以高效地完成數據點的分配。

2 自動確定聚類中心的比較密度峰值聚類算法

2.1 比較量

依據密度峰值聚類算法第二個假設的描述，即聚類中心與比其密度高的數據點的距離相對較遠可知，聚類中心點的δi值一定相對較大。原算法對于“相對較大”的概念只是讓用戶在決策圖的可視化分析中進行比較，然而決策圖中不是所有的聚類中心點都能體現出來，并且有時聚類中心點與非聚類中心點在決策圖中顯示不夠清晰。借鑒文獻［23］思想，本文采用比較量d來替代δ，實現定量比較的方式來顯示相對距離，從而凸顯聚類中心。

本文用τi作為數據點i與其密度更低點的最短距離，具體定義如下：

式（5）中當數據點i的局部密度為最小值時，它的τi值為δi值。τi值的定義作為與δi值正好相反的一個距離屬性，為了描述其差值，用d來表示，其定義如下：

di為δi與τi的比較數量，有助于識別潛在的聚類中心。如圖2（b）所示，當di值較大時，表明該數據點距離低密度區域的數據點很近而距離更高密度的數據點更遠，符合聚類中心的選擇特征。當di的值在零附近，表明該數據點既有密度更大的數據點也有密度更小的點，說明該數據點處于某個類簇中。若di遠小于零，該數據點距離密度高的數據點較近而距離密度低的點較遠，這類點為類簇邊緣點。

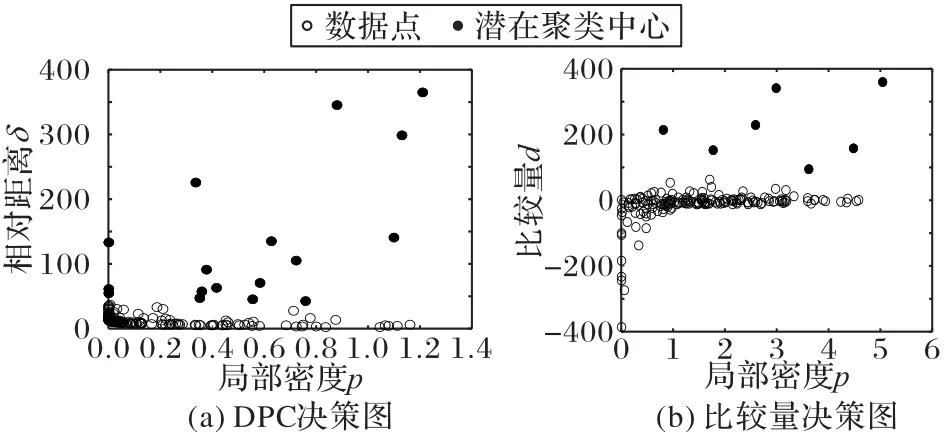
圖2 決策圖對比Fig.2 Decision diagram comparison

2.2 基于統計分析的聚類中心點自動識別

DPC 算法在選取聚類中心時設計了一種啟發式方法，在決策圖上手動選擇同時具備高密度和高距離的數據點作為聚類中心。這種方法雖然可以人為地在決策圖上可視化地識別聚類中心，但只是在數據集分布清晰的條件下能有較好的識別效果，當處理大規模數據并且具有復雜的決策圖時，人為的方式就難以保證聚類結果較高的準確性。針對該問題，借鑒文獻［24］思想，本文采用特定統計量來實現聚類中心點的自動識別。

根據數據點在決策圖中的分布特征，用高斯核函數來估計特定密度值pi處的概率密度ρy(pi，y)，其定義如下：

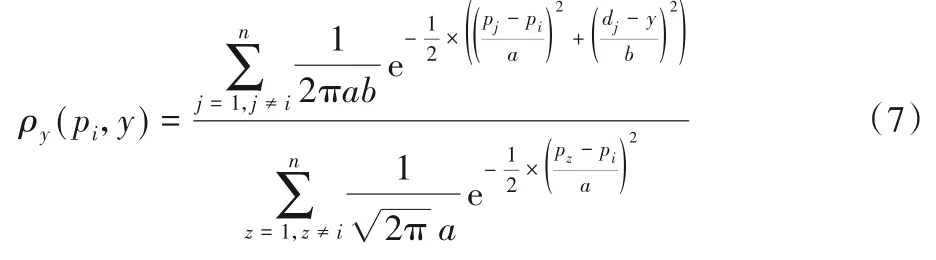
其中：y表示特定密度值pi處可能的距離值。數值n為數據點的總數，參數a、b為核寬度值。分母是一個歸一化的因子，可以確保(pi，y)=1。核寬度a和b作為概率密度估計重要的參數，通過pi和di的標準差估計得到，rp和rd設置為0.5，具體定義如下：

根據式（8）得到的概率密度估計，然后在特定密度值pi對最小距離值y的期望值和方差值進行估計，其定義如下：

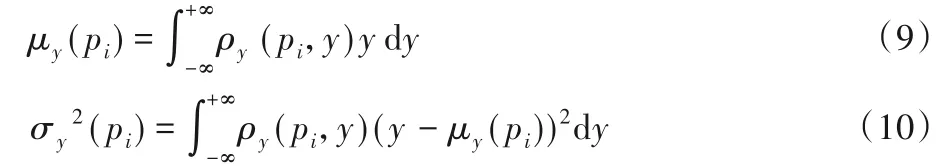
通過化簡可以得到：

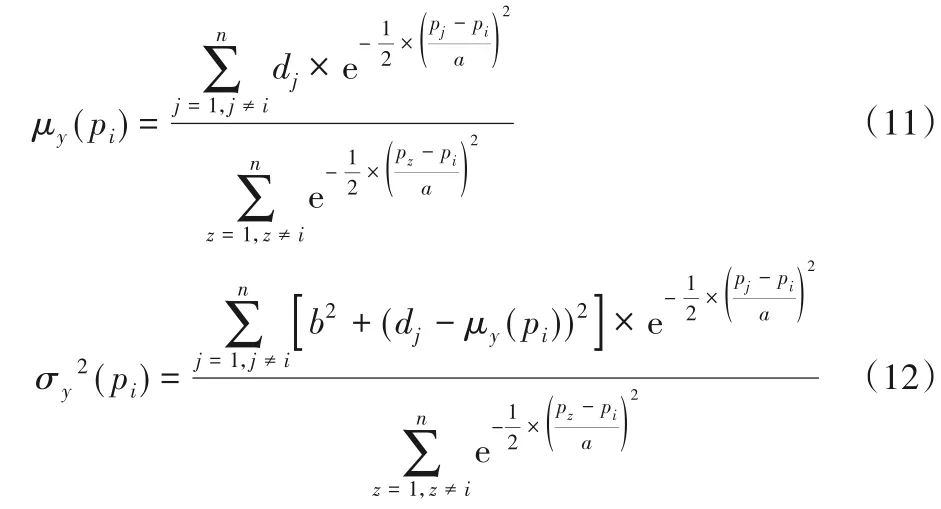
式（11）、（12）中，n為數據點總數，pi表示數據點i的局部密度，參數a、b表示核寬度值，dj表示比較量。

完成在特定密度值pi處最小距離y的期望值和方差值的計算后，利用以下公式進行聚類中心的自動化識別：

根據式（13）可知：μy(pi)表示y的期望值，σy(pi)表示y的標準差。如果數據點的最小距離值di＞THd(pi)，它將會自動識別為聚類中心點。為了便于了解自動化識別聚類中心算法，圖3 進行了直觀描述，其中黑色圓形點為聚類中心，菱形為期望值，正方形為標準差。

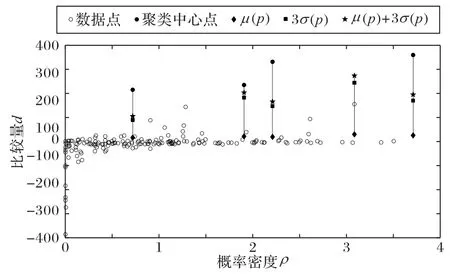
圖3 用于聚類中心點自動識別的統計量Fig.3 Statistics for automatic recognition of clustering center points

2.3 算法的主要步驟描述

ACPC算法的具體實現步驟如下：

2.4 時間復雜度分析

ACPC 算法的時間復雜度主要有4部分［25］構成：1）計算相似度矩陣，其時間復雜度為O(n2)；2）求每個數據點的比較量d，其中距離δ的時間復雜度為O(n2)，對比量τ的時間復雜度為O(n)，比較量d時間復雜度為O(n2)，所以計算每個數據點的比較量d的整體時間復雜度為O(n2)；3）對特定密度值pi處最小距離值y的期望值和方差值估計，時間復雜度為O(n2)；4）分配樣本的時間復雜度與DPC 中相應操作的時間復雜度相同，為O(n2)。因此，ACPC算法的整體時間復雜度為O(n2)。

3 實驗仿真及分析

選用人工數據集和UCI（University of California lrvine）［26］公開數據進行實驗驗證，數據集的詳細信息如表1 所示，并將其與DPC、基于KL 散度的密度峰值聚類算法（Density Peaks Clustering based on Kullback-Leibler divergence，KLDPC）、改進的快速搜索與發現密度峰值聚類（Clustering by Fast Search and Find of Density Peaks，CFSFDP）、APC（density-based Clustering using Automatic density Peaks detection）、自動確定聚類中心的快速搜索和發現密度峰值的聚類算法（AUTOmatic determination of clustering center for CFSFDP，AUTO-CFSFDP）算法［27］進行比較，各算法在不同數據集上的參數取值如表2 所示。實驗開發環境Matlab2014a，硬件條件為：Intel Core i5-3470 CPU，主頻3.20 GHz，內存4.00 GB。

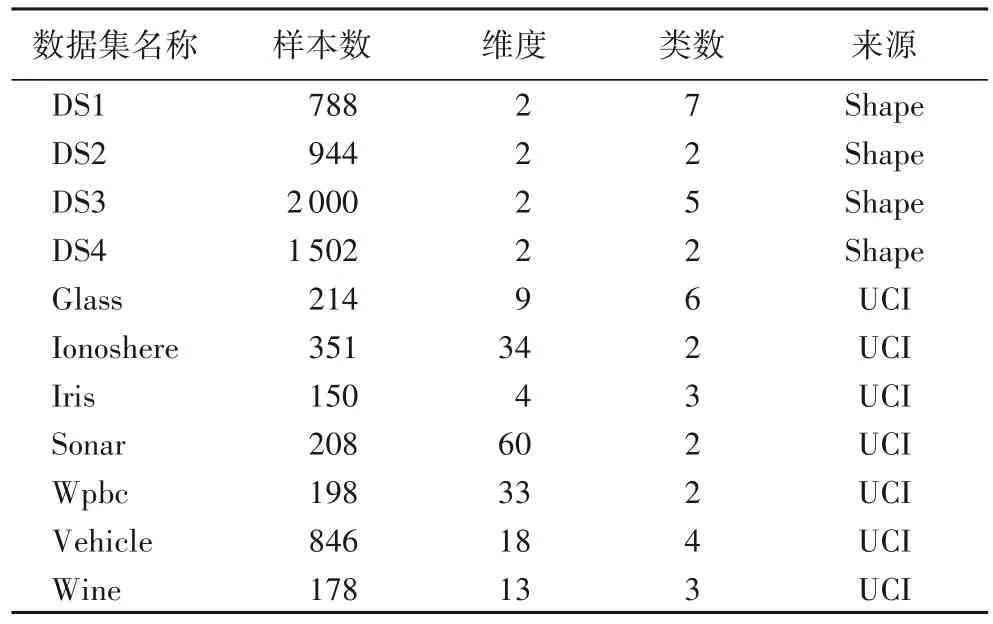
表1 數據集信息Tab.1 Information of datasets

3.1 人工數據集的實驗結果分析

本文采用4 個人工數據集驗證ACPC 的聚類效果，圖4 為實驗數據的二維圖形展示，圖5～8 為各算法分別對DS1～DS4的聚類結果。

圖5 為DS1 在五種算法中得到的聚類結果。DPC 算法、APC算法、ACPC算法都可以準確確定聚類個數且聚類效果都很好。KLDPC 算法、改進的CFSFDP 算法、AUTO-CFSFDP 算法不能正確聚類，錯誤地將多個球形數據聚為一個類簇。

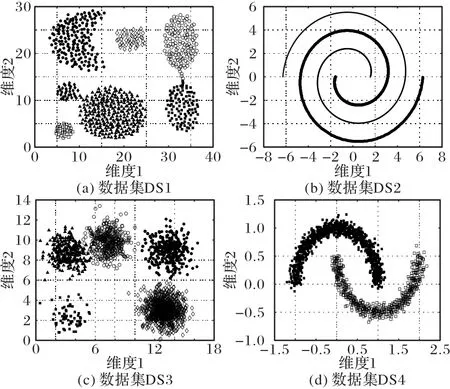
圖4 實驗數據的二維圖形展示Fig.4 2D shapes of experimental data

圖6 為DS2 在五種算法中得到的聚類結果。DPC 算法、KLDPC 算法、APC 算法、AUTO-CFSFDP 算法、ACPC 算法對數據集都有很好的聚類效果。改進的CFSFDP 算法對環形數據集聚類結果不理想，錯誤地將兩個類簇的數據點聚類成一類。

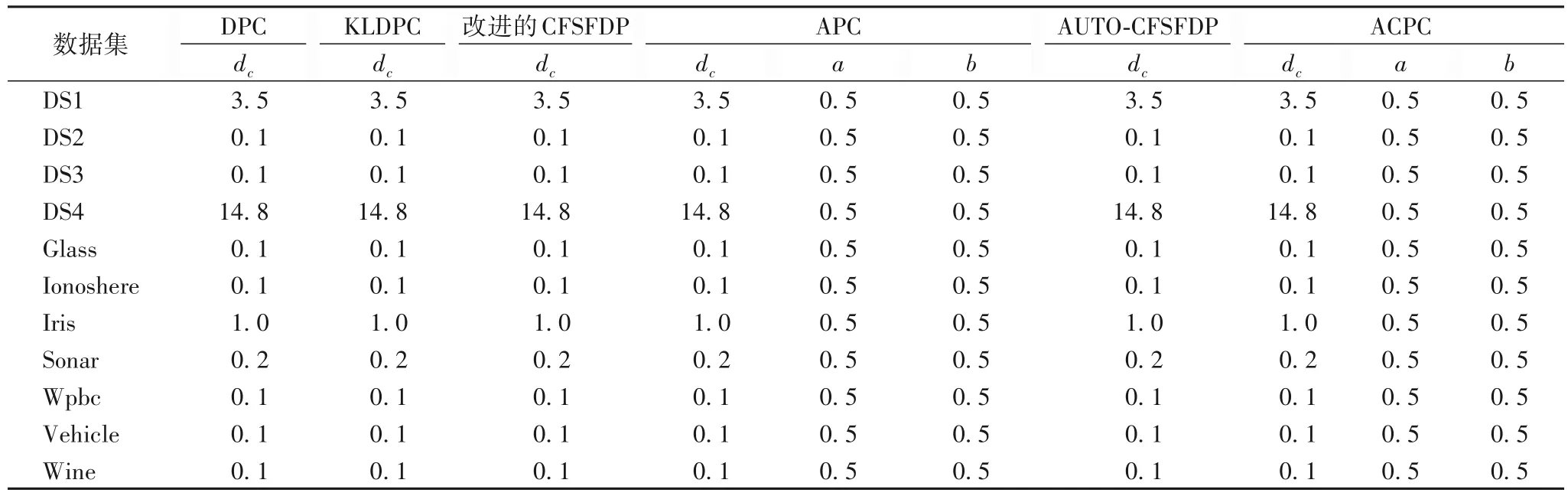
表2 各算法在11個數據集上的參數取值Tab.2 Parameters of different algorithms on 11 datasets

圖7 為DS3 在五種算法中得到的聚類結果。DPC 算法、改進的CFSFDP 算法、ACPC 算法能準確確定聚類個數，但在兩個離得近的球形數據上沒能正確分配。KLDPC 算法得不到數據集聚類中心點的準確個數，將五個類簇劃分為兩個類簇。APC 算法錯誤地將一個簇類分成多個類簇。AUTOCFSFDP算法不能正確確定聚類個數，錯誤地將數據密集的類簇識別為多個類簇。

圖8 為DS4 在五種算法中得到的聚類結果。ACPC 算法對DS2 簡單流形數據能很好聚類，對于DS4 數據錯誤地將一類聚成兩類。DPC 算法、KLDPC 算法、改進的CFSFDP 算法、APC算法、AUTO-CFSFDP算法在聚類效果上很不理想。

3.2 UCI數據集的實驗結果分析

為了進一步驗證ACPC 算法的性能，采用準確率（Accuracy，ACC）與標準互信息（Normalized Mutual Information，NMI）兩類聚類指標對本文算法和現有算法進行了性能對比，加粗的數據為數據的最優聚類結果。表3 為聚類結果的性能對比。

已知真實類劃分U={U1，U2，…，UT}，V={V1，V2，…，VT}為聚類結果。

定義3準確率（ACC）：

其中，ncorrect代表分類正確的記錄個數，ntatol代表全部測試數據的個數。當預測結果與真實結果完全相符時準確率為1，兩者越不相符準確率越低。

定義4標準互信息（NMI）：

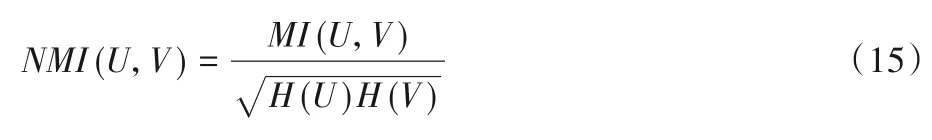
其中：H(U)和H(V)是U和V兩種分布的熵，MI(U，V)是U與V之間的互信息，NMI 取值范圍為［0，1］，值越大意味著聚類結果與真實情況越吻合。每一部分的計算見文獻［28］。

由表3 可知，ACPC 算法在準確率上，除了在Sonar 數據集上聚類效果差一些，在其他數據集上都達到了最優。在標準互信息上，ACPC在Iris和Wine數據集上要優于其他算法，在其他數據集上略差一點。綜合這兩種聚類指標來看，ACPC算法優于DPC、KLDPC、改進的CFSFDP、APC、AUTO-CFSFDP算法。

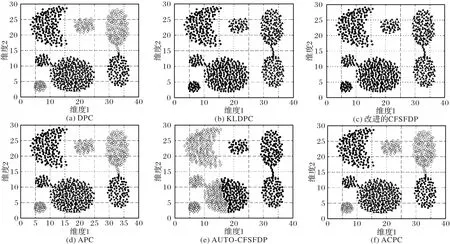
圖5 五種算法在DS1數據集上的聚類結果Fig.5 Clustering results of five algorithms on DS1 dataset

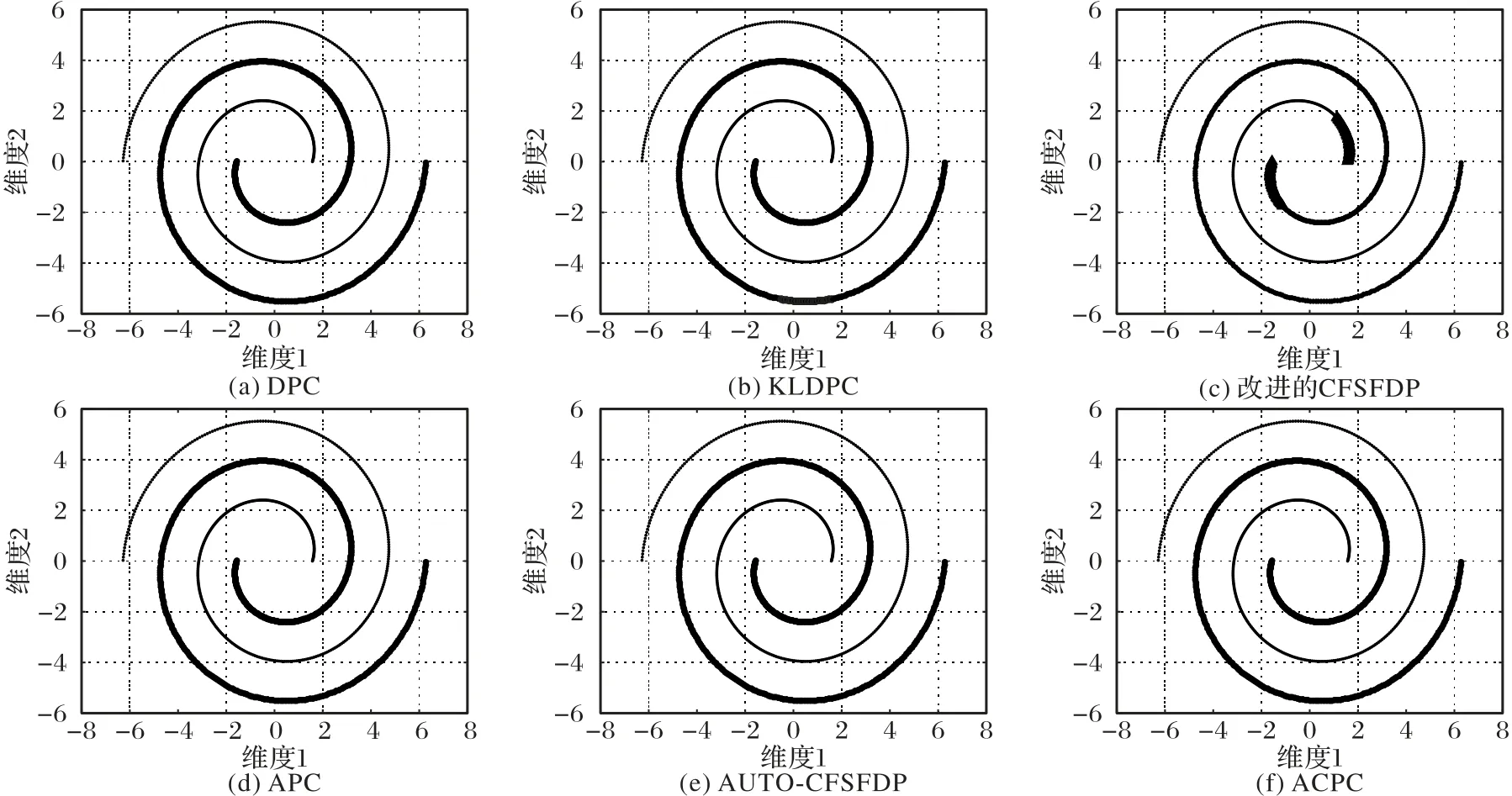
圖6 五種算法在DS2數據集上的聚類結果Fig.6 Clustering results of five algorithms on DS2 dataset

4 結語

針對DPC 需要手動選取聚類中心，以及在處理密度變化較大的數據集時生成的決策圖聚類中心和非聚類中心不夠清晰的問題，實現了一種無須人工交互選擇聚類中心的比較密度峰值聚類算法。該算法通過統計分析的二維區間估計方法實現對聚類中心的自動選取，同時采用距離的比較量di來代替原算法的δi，使潛在的聚類中心在決策圖中更加突出。通過對人工和UCI 數據集的實驗驗證，并與其他算法的對比分析，本文算法不僅能夠自動選取聚類中心，實現了聚類過程的自動化，并且具有更好的準確性以及適用性。如何自動地確定最佳的截斷距離以及將DPC 算法應用于實際問題將是下一步的研究重點。

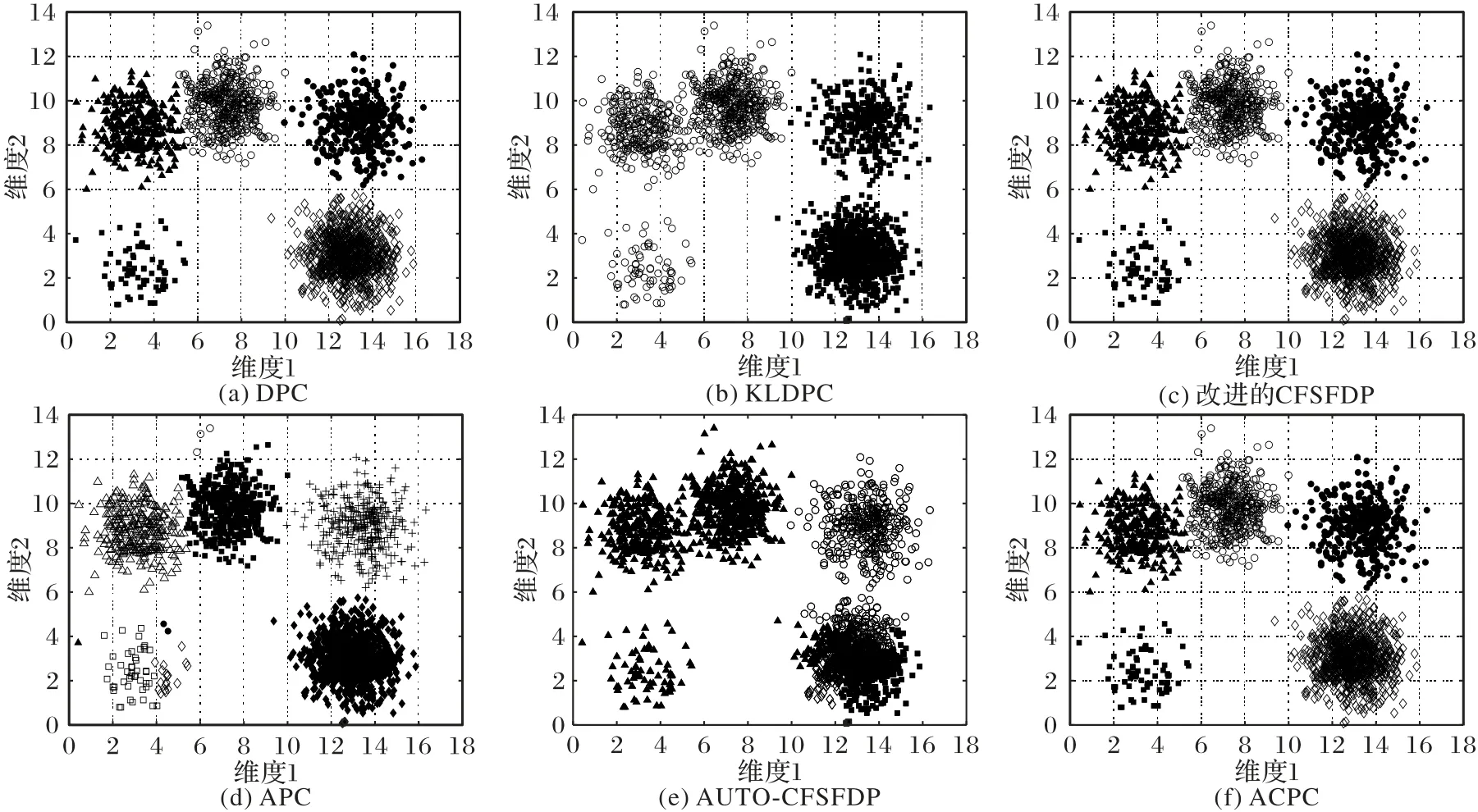
圖7 五種算法在DS3數據集上的聚類結果Fig.7 Clustering results of five algorithms on DS3 dataset

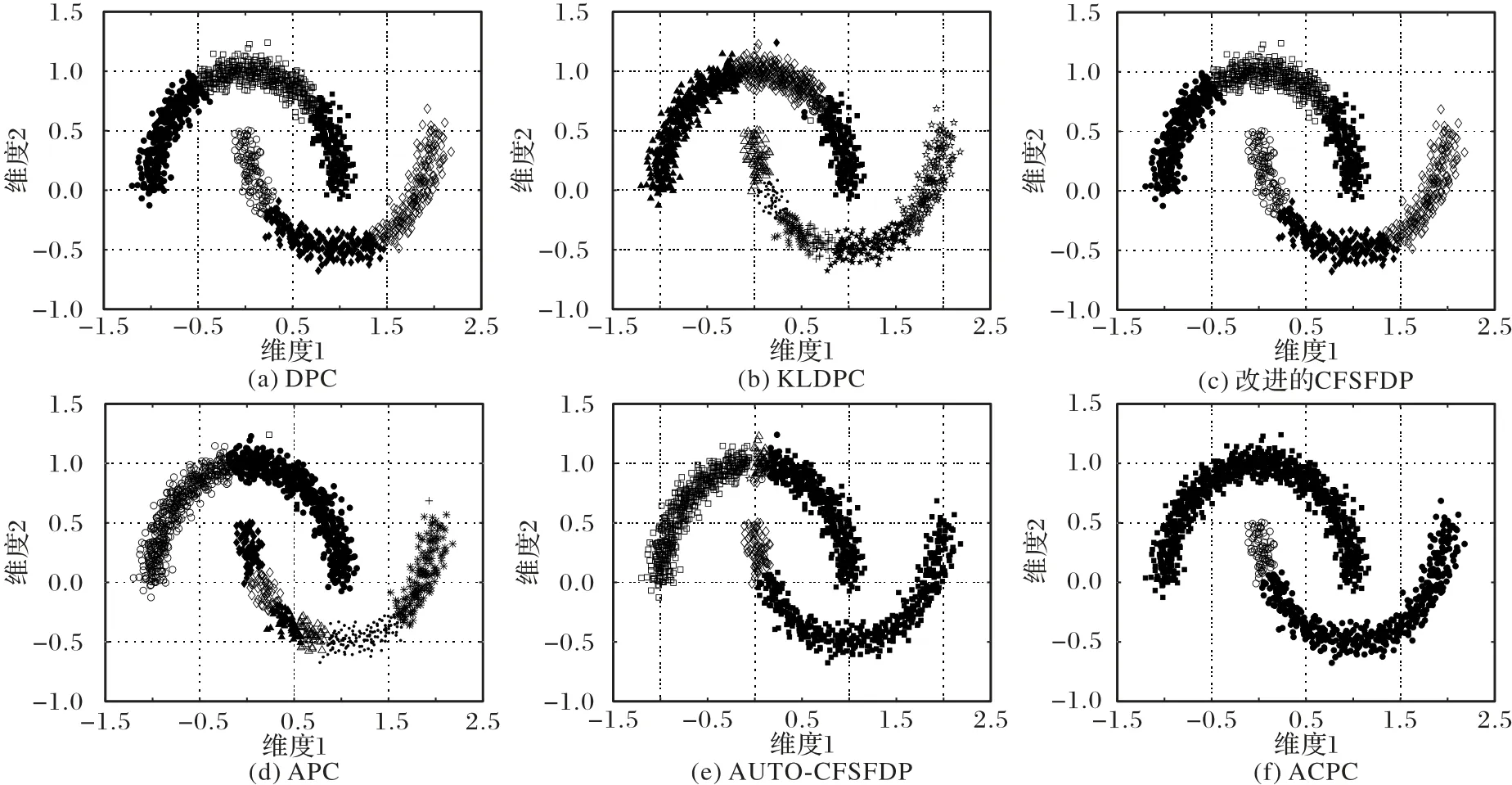
圖8 五種算法在DS4數據集上的聚類結果Fig.8 Clustering results of five algorithms on DS4 dataset

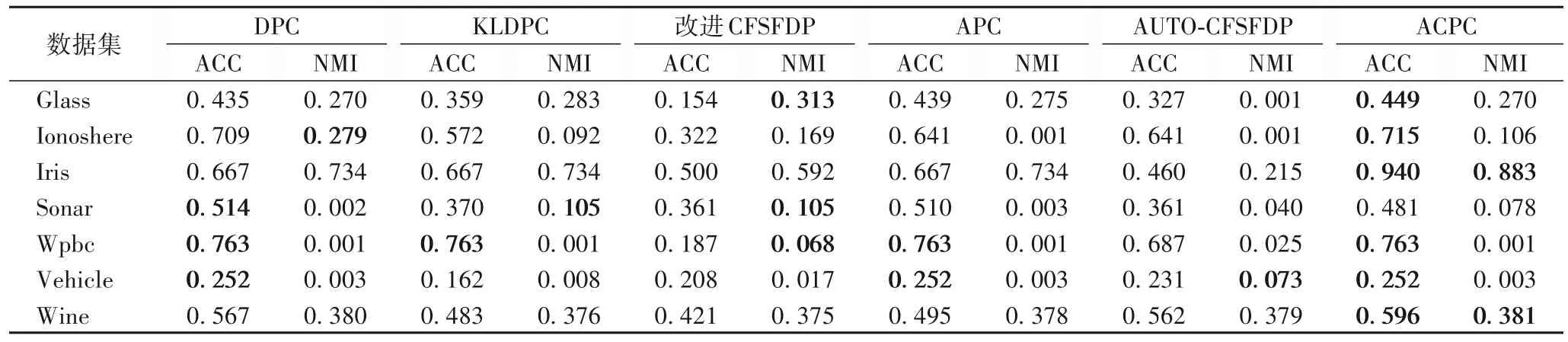
表3 聚類結果對比Tab.3 Comparisin of clustering results