基于改進粒子群優化和極限學習機的網絡安全態勢預測

（1.空軍工程大學研究生院，西安 710051；2.空軍工程大學防空反導學院，西安 710051）

0 引言

隨著大數據時代的到來，網絡給人們帶來了極大的便利，但同時由于安全意識的缺乏，網絡也帶來了不可估量的安全問題。原始的網絡安全預防主要通過防火墻、殺毒軟件等技術被動防御外來的網絡入侵，無法預測未來的走向。網絡安全態勢預測能夠對網絡狀態進行分析，預測將來發生的狀況，可在網絡受到危險之前制定安全防范措施。因此，設計出有效、準確的網絡安全態勢預測模型是由被動防御轉為主動防御的關鍵一步。

目前對網絡安全態勢預測模型的研究方法各種各樣［1］，傳統的預測模型基本分為三種：統計分析模型、數據驅動模型和定性知識模型。統計分析模型如灰色預測需要建立精準的數學表達式，計算量大，且只能預測態勢的大致趨勢，不能預測精準的態勢值；數據驅動模型如反向傳播（Back Propagation，BP）神經網絡需要利用大量的定量數據對模型進行優化訓練，學習速度低，易出現過擬合、收斂慢等不足；定性知識模型只憑借專家經驗及定性描述的數據無法有效利用定量信息，會出現組合爆炸及預測結果不準確等問題。文獻［2］提出利用改進灰色關聯理論對收集到的異常流量進行關聯分析，實現校園網的態勢感知，數據量運算大。文獻［3］用BP 神經網絡作為預測模型，通過人群搜索算法優化其參數，實現了更好的穩定性，但增加了訓練時間成本。文獻［4］采用模擬退火與高斯擾動的粒子群與支持向量機結合的預測模型，提高了預測精度，但收斂慢。文獻［5］提出隱置信規則庫模型，綜合了專家經驗和實驗數據，成為復雜系統隱行為預測的一種有效方法。綜合上述所提方法的優缺點，需要進一步尋求更優算法建立網絡安全態勢預測模型。極限學習機（Extreme Learning Machine，ELM）［6］是一種基于單隱含層前饋神經網絡的最新研究成果，彌補了傳統神經網絡過擬合、收斂慢等缺陷。同時隨著啟發式算法的快速發展，眾多學者對大量傳統的啟發式算法本身進行改進，進而優化神經網絡，使其產生更好的訓練效果。文獻［7］提出一種改進遺傳算法（Genetic Algorithm，GA），對遺傳算法的種群、適應度函數、交叉概率及變異概率進行了改進，保持了種群的多樣性的同時，避免了早熟收斂。文獻［8］提出一種針對粒子群優化（Particle Swarm Optimization，PSO）算法收斂慢的改進，綜合了指數衰減慣性權重和增強控制的學習因子，可以在較少的迭代次數獲得更好的優化效果。文獻［9］將粒子群算法與支持向量機結合進行網絡安全態勢預測，表明了該方法的可行性，實現對網絡安全威脅的有效防御，但支持向量機本身并不能進行大規模樣本訓練。文獻［10］將GA 與ELM 結合建立GA-ELM 預測模型，具有更高的預測精度和更好的泛化能力，但遺傳算法的收斂始終較慢。文獻［11］提出PSO 與ELM 組合算法，避免了ELM網絡不穩定問題。

綜上，基于ELM 的快速收斂能力及PSO 的穩定尋優性能，本文提出了一種改進粒子群優化極限學習機（Improved Particle Swarm Optimization Extreme Learning Machine，IPSOELM）算法的網絡態勢預測方法，通過改進PSO自適應調整全局和局部尋優能力優化ELM，使預測結果更加準確，并在保持快速收斂的同時，提高算法的穩定性。實驗結果表明，所提方法比傳統ELM、文獻［10］中GA-ELM 算法和文獻［11］中PSOELM 算法能獲得更高精度的預測結果，同時建模效率也得到明顯的提高。

1 極限學習機

極限學習機最早在2004 年被Huang 等［6］提出，通過隨機選取輸入層權重和隱含層偏置，以單隱層前饋神經網絡為基礎，依據Moore-Penrose 廣義逆矩陣理論計算解析得出輸出層權重，具有訓練參數少、學習速度高、泛化能力強的優點。假設ELM 輸入層、隱含層和輸出層節點個數為分別n、l、m，其網絡結構如圖1所示。

對于給定的N個任意不同樣本(xi，ti)，其中xi=(xi1，xi2，…，xin)T，ti=(ti1，ti2，…，tim)T，則ELM的輸出為：

其中：wi=(wi1，wi2，…，win)T為輸入層神經元與隱含層神經元之間的輸入權值；βi=(βi1，βi2，…，βim)T為隱含層神經元與輸出層神經元之間的輸出權值；bi為隱含層神經元的偏置；g(?)為隱含層神經元的激活函數。ELM系統的矩陣表達式為：

其中：

其中：H為ELM 網絡的隱含層輸出矩陣；T為網絡的樣本期望輸出矩陣。最終通過求解得到輸出權值為：

其中H?為輸出矩陣的Moore-Penrose廣義逆矩陣。

由此得出，ELM在訓練樣本時無需借助梯度下降法，與傳統的借助梯度下降法的反向傳播神經網絡相比，極大地減少了訓練時間，同時保留了較為精確的預測能力。

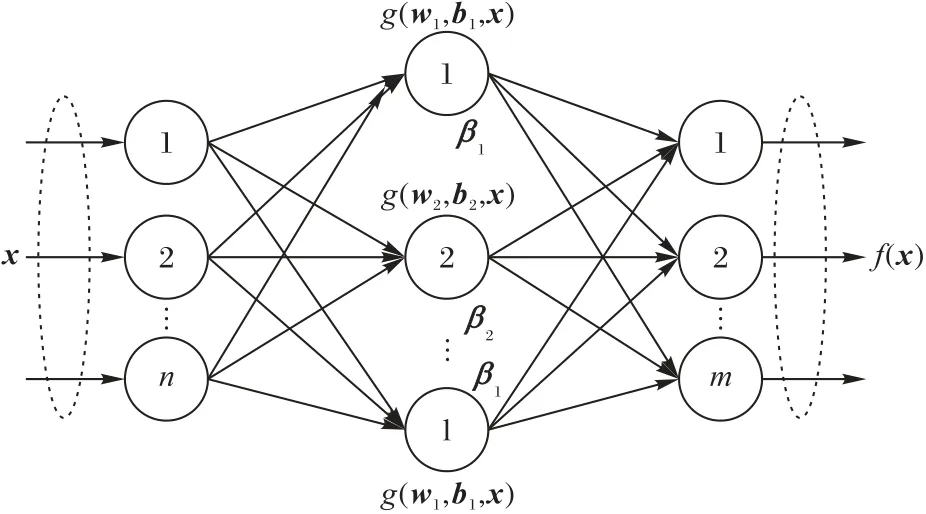
圖1 ELM網絡結構Fig.1 Network structure of ELM

2 改進粒子群優化極限學習機

2.1 粒子群優化算法

粒子群優化算法最早是由Kennedy 等［12］于1995 年提出：在一個D維目標搜索空間中，存在某個包含a個粒子的群體，該群體中每個粒子都有一個初始速度vk、初始位置sk及適應值gk。在每一次迭代中，每個粒子不斷更新著自己的位置和速度，同時通過適應值判斷更新個體的最優位置pk和種群的最優位置pg。假設第一次迭代時最優位置即為粒子的初始位置，因此，種群中粒子的速度和位置的更新公式為：

其中：k代表粒子群中的第k個粒子；u代表目前的迭代步數；z稱為慣性因子，其值為非負，當z較大時，全局尋優能力強，z較小時，全局尋優能力變弱。通過對z的大小進行調整可以控制粒子全局尋優和局部尋優的能力；c1、c2分別是粒子的個體學習因子和社會學習因子，其值為非負常數；r1、r2為在［0，1］范圍內互相獨立的隨機數。

2.2 粒子群優化極限學習機模型

由于隨機給定ELM 的輸入權值矩陣和隱含層偏差，可能部分數值為0，使一些隱含層節點失效，從而導致預測效果不佳、穩定性不足等問題。為達到預測精度只有提高隱含層節點的數目，但隱含層節點數目的提高會出現訓練樣本適應能力差、泛化能力降低的問題。因此，為了保證ELM 在最優隱含層節點的條件下同時具有較高的預測精度，采用PSO 算法對其優化，借助PSO 的全局搜索能力將ELM 的輸入權值和隱含層偏差進行最優搜索，既增強了ELM 的穩定性，又不會降低ELM 的收斂速度，在ELM 訓練輸入樣本的過程中更加深入地學習樣本之間的各種關系，其算法流程為：

步驟1 將樣本數據分為訓練樣本和測試樣本。

步驟2 通過樣本數據確定ELM網絡拓撲結構。

步驟3 初始化PSO 參數，種群的每個粒子代表連接權值和隱含層偏差，ELM 訓練樣本的均方根誤差作為適應度函數。

步驟4 構建的訓練樣本輸入ELM，根據ELM 得到的預測值評價每個粒子的適應度。

步驟5 令粒子k(k=1，2，…，a)，當前的最優位置為pk=sk，對應的適應度為gbestk=gk；從粒子群中找出全局最優粒子，令其位置為pg，對應的適應度為gbest。

步驟6 對所有粒子執行如下操作：

1）按式（5）、（6）重新計算每個粒子的速度、位置，同時計算其適應度gk。

2）若gk＞gbestk，則pk=sk，gbestk=gk；若gk＞gbest，則pg=sk，gbest=gk。

步驟7 判斷是否達到最大迭代次數，或適應度值是否達到給定的閾值，若否，轉至步驟6；否則轉至步驟8。

步驟8 將最終獲得的權值和閾值作為ELM 的連接權值和偏差。

步驟9 將獲得的最優權值和偏差應用到ELM 中預測得到結果。

2.3 IPSO-ELM的網絡安全態勢預測模型

雖然PSO-ELM 的預測能力有了較大提高，但PSO 在進行全局搜索時容易陷入局部最優點，這導致PSO-ELM算法穩定性較差。目前已有的方法包括對慣性權重的線性遞減策略仍然不能權衡粒子的全局與局部搜索能力。為了解決這個問題，文獻［13］中提出將目前迭代次數與最大迭代次數的比值作為慣性權重的變化，有效平衡了全局與局部的搜索能力，但不同的最大迭代次數之間相互比較發現，慣性權重變化量的突變使PSO-ELM算法的穩定性降低。同時，文獻［14］研究指出慣性權重因子落在［0.3，0.7］為最佳區間，在此區間可更好地平衡算法的局部和全局搜索能力。因此，本文從PSO的慣性權重及學習因子入手，將靜態參數改為可以隨著迭代次數增加而自適應調整的動態參數，使z在迭代過程中更多地處于最佳位置，并且不同的最大迭代次數對慣性權重變化趨勢的影響不大，同時提出了一種基于粒子個體隨機擾動處理的策略，使陷入局部極值點的個體重新進行全局搜索。慣性權重調整公式如下：

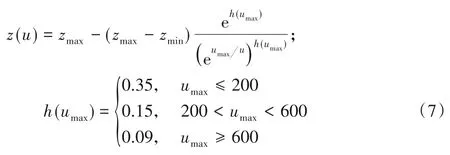
其中h(umax)代表最大迭代次數的函數。如圖2 所示，多個不同的最大迭代次數產生的慣性權重變化趨勢相差不大，對算法的穩定性有所增強。

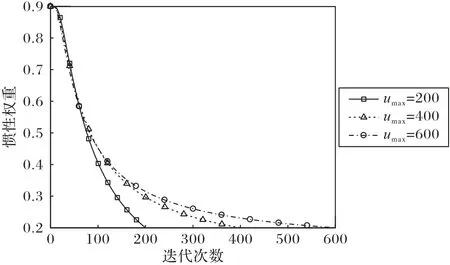
圖2 慣性權重與迭代次數關系Fig.2 Relationship between inertia weight and iteration times

學習因子的調整方法為：算法在搜索前期，使c1值大于c2值，粒子主要進行全局搜索，避免陷入局部極值點；算法在搜索后期，使c1值小于c2值，粒子最終聚攏到全局最優區域。文獻［15］指出c1的最佳取值范圍為［2.5，0.5］，c2的最佳取值范圍為［0.5，2.5］。因此學習因子的調整公式為：

圖3 學習因子與迭代次數關系Fig.3 Relationship between learning factor and iteration times

為解決種群粒子在搜索空間飛行尋找最優解時易陷入局部最優的問題提出粒子擾動處理策略，當判定粒子個體發生停滯狀態時，通過停滯擾動處理，使個體粒子跳出局部最優，其判定處理公式為：

其中：ep為當前個體與局部最優個體之間的偏差；eop為當前個體與局部最優個體之間的閾值。

綜上，經過改進的種群中粒子的速度和位置更新公式為：

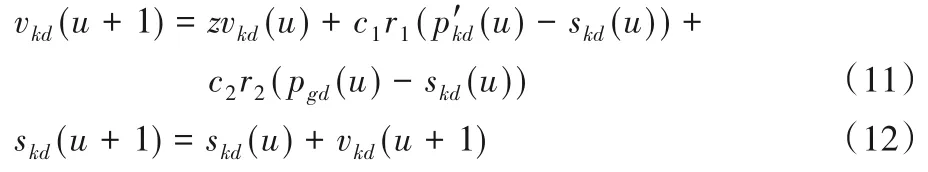
最終，得到IPSO-ELM 的網絡安全態勢預測流程如圖4所示。

圖4 IPSO-ELM預測流程Fig.4 Flowchart of IPSO-ELM prediction

3 預測結果與分析

3.1 實驗數據及其預處理

本文的實驗數據來自文獻［16］中搭建的網絡環境所得出的網絡安全態勢值。該網絡環境如圖5 所示，首先模擬真實的黑客攻擊行為，主要進行各種漏洞攻擊；其次，通過對攻擊的次數、種類進行統計，并判斷主機遭受攻擊后的受損程度建立網絡安全評估系統來綜合得出當前階段的網絡安全態勢。實驗中每隔30 min 進行一次統計并評估計算網絡安全態勢值，最終選取100 個態勢值組成樣本數據，并通過歸一化處理排除誤差偏大的可能，使網絡安全態勢值處于［0，1］區間，如圖6所示。

圖5 網絡實驗環境Fig.5 Network experiment environment

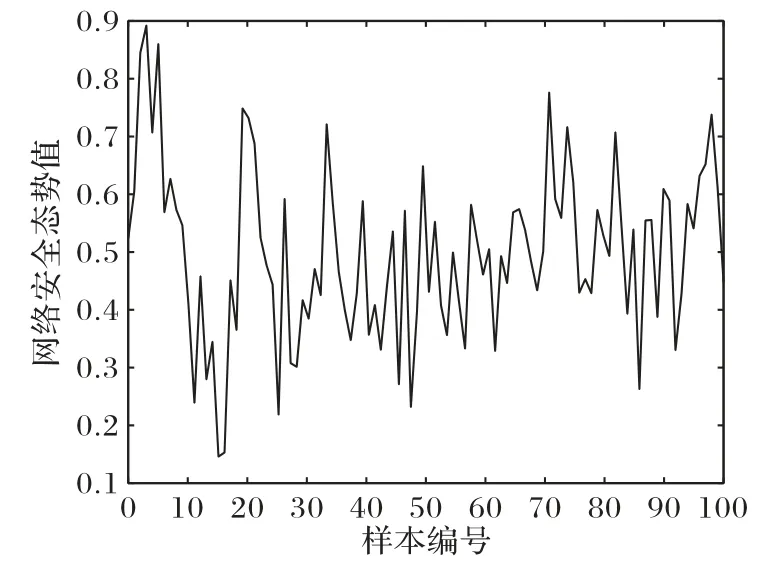
圖6 網絡安全態勢值Fig.6 Network security situation value

3.2 結果分析

實驗過程中需要確定ELM 神經網絡的各項參數，由于ELM 的輸入層神經元個數代表樣本數據的維數特征，而本文所對應的是某一段時間的網絡安全態勢值，所以采用滑動窗口法實現ELM 的輸入數據。經過對網絡安全態勢的分析得出，一般網絡當前的態勢與之前3～5 個時間點存在著某種聯系，因此將滑動窗口o的大小分別設置為3 和5 進行預測實驗。隱含層神經元的個數對最終實驗結果有一定影響，采用試錯法確定隱含層神經元的個數，由于隱含層神經元個數通常不超過輸入層神經元個數，所以隱含層神經元個數從1 開始依次增加到5，最終選取隱含層神經元個數為4。本文的目的是對未來的網絡態勢進行預測，因此輸出層神經元個數為1，代表下一個時間段的網絡安全態勢值。

為了評價網絡態勢預測結果的優劣，選擇平均相對誤差（Mean Relative Error，MRE）、均方誤差（Mean Square Error，MSE）、平均絕對誤差（Mean Absolute Error，MAE）和擬合優度決定系數（the coefficient of determination，R2）作為預測結果的評價指標，其中MRE 的大小反映測量的可信度；MSE 的大小評價數據變化程度，其值越小，表明模型有更好的預測精度；MAE更好地反映預測值誤差的實際情況。各評價公式為：

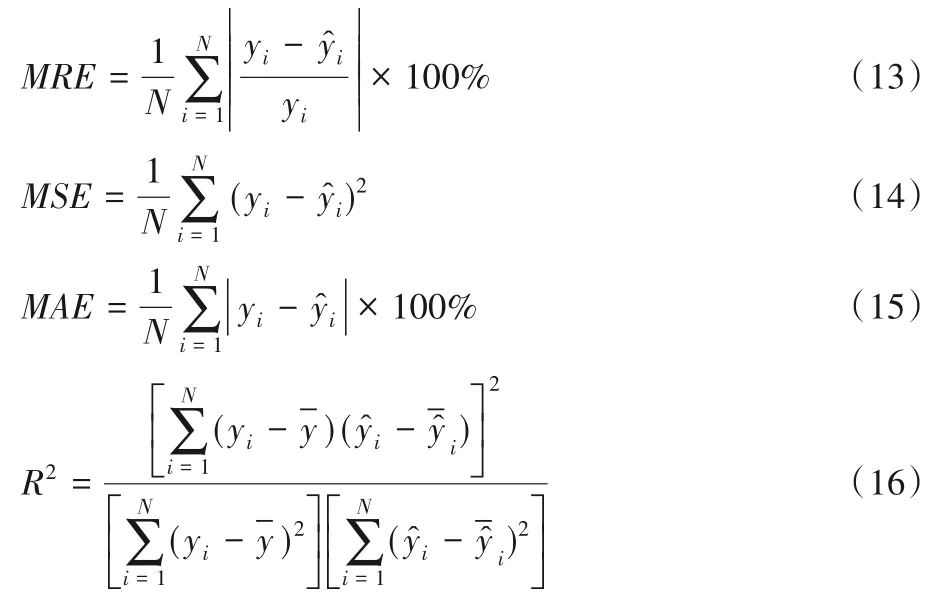
其中：yi為某一樣本的實際值為某一樣本的預測值；N為樣本數為實際值的平均值為預測值平均值。

當滑動窗口的窗口值為3 時，采用前三個時間段的態勢值預測下一個時間段的態勢，其中部分樣本已給出，見表1。經過IPSO-ELM 的預測，與傳統的ELM、GA-ELM 及PSO-ELM對比，得出實驗結果如圖7 所示，各算法的收斂速度及評價指標對比如表2所示。

表1 部分樣本輸入輸出（o=3）Tab.1 Inputs and outputs of some samples（o=3）

通過預測仿真得到如圖7及表2對比結果。

當滑動窗口值為5 時，部分樣本見表3，實驗結果對比見圖8，評價指標對比如表4所示。

圖7 窗口值為3時的實驗結果Fig.7 Experimental results with window value of 3

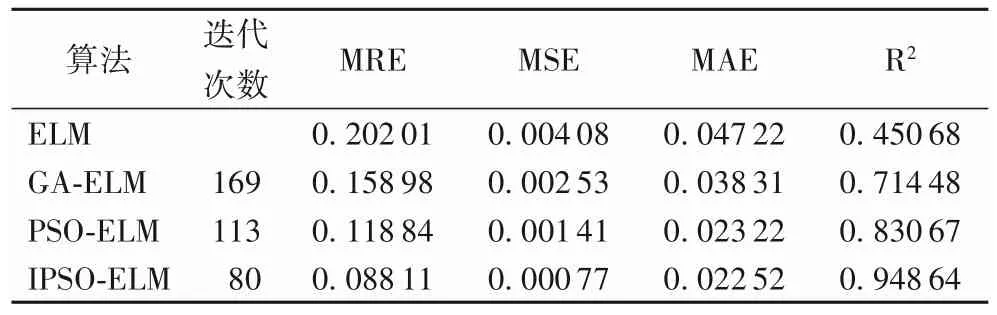
表2 迭代次數和評價指標對比（o=3）Tab.2 Comparison of iteration times and evaluation indexes（o=3）

表3 部分樣本輸入輸出（o=5）Tab.3 Inputs and outputs of some samples（o=5）

表4 迭代次數和評價指標對比（o=5）Tab.4 Comparison of iteration times and evaluation indexes（o=5）

通過實驗結果對比分析可以看出，當滑動窗口值固定時，本文提出的IPSO-ELM 算法相較PSO-ELM 和GA-ELM 算法在網絡安全態勢訓練數據的擬合度更高，對預測數據的準確性也有較大提高。雖然相較于ELM 收斂變慢，但當滑動窗口值為3 時，IPSO-ELM 比PSO-ELM 及GA-ELM 的收斂速度分別提高了29.2%和52.66%；當滑動窗口值為5 時，收斂速度分別提高了47.43%和66.94%。

對本文實驗而言，當滑動窗口值不固定時，窗口值越大，訓練輸入數據時更能深度學習到數據之間存在的關系，從而對下一時間段的預測有一個更好的效果。

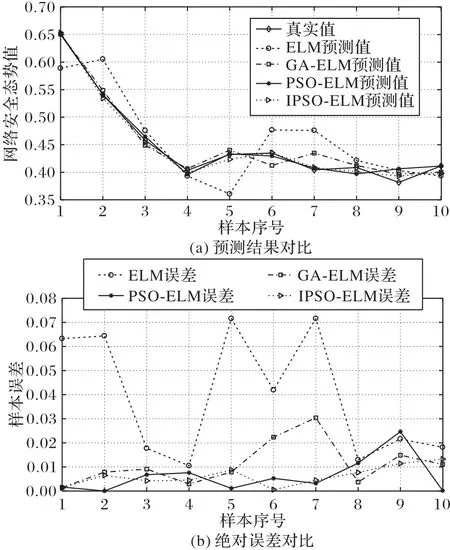
圖8 窗口值為5時的實驗結果Fig.8 Experimental results with window value of 5

4 結語

針對網絡安全態勢預測精度問題，本文提出了IPSO-ELM模型。ELM 神經網絡可以快速地訓練樣本，加上IPSO 對其初始權值進行優化，可以精確地預測下一步的網絡安全態勢。經過實驗對比表明，IPSO-ELM 模型在真實的網絡環境中相較于GA-ELM 及PSO-ELM 有一定的優越性，收斂速度高，預測精度更高。但IPSO-ELM 也存在不足，在隱含層節點選取過程中偶然性較大，同時對于滑動窗口法窗口值的過大出現過擬合現象也未曾考慮，接下來將進一步研究自適應隱含層節點個數，從而更進一步提高收斂速度及預測精度。