模糊需求下低碳取送貨車輛調度問題與算法

*

（1.河北工業大學經濟管理學院，天津 300401；2.河北工業大學財務處，天津 300401）

0 引言

隨著社會經濟的飛速發展，溫室氣體排放量急劇增加，環境污染問題引起了全球各國的高度重視。物流運輸行業作為一個高能源依賴行業，據相關統計，碳排放量占全球總排放量18%。在國家大力推行節能減排的背景下，合理的配送路徑規劃不僅可以幫助企業有效降低物流運輸成本，而且有利于降低運輸過程中的能源消耗，從而減少碳排放量，帶來更好的環境效益和經濟效益。

近幾年，低碳車輛調度問題逐漸受到各領域專家和學者的關注。何東東等［1］引入碳排放量和油耗的近似計算方法，建立成本最小化的帶時間窗多車型綠色車輛調度問題（Green Multi-type Vehicle Routing Problem with Time Window，G-MVRPTW）模型。唐慧玲等［2］研究帶有碳排放約束的車輛調度問題，構建車輛行駛路徑最短和碳排放量最小的多目標函數模型，并采用改進的蟻群算法求解模型。張明偉等［3］針對車輛在配送過程中產生大量碳排放問題，建立碳排放量最小、服務時間最短以及行駛路程最小的多目標模型。周鮮成等［4］針對時間依賴型綠色路徑問題，構建車輛碳排放成本、油耗成本、車輛使用時間成本和人力成本、固定發車費用等成本之和最小的時間依賴型綠色車輛調度（Time-Dependent Green Vehicle Routing Problem，TDGVRP）模型。葛顯龍等［5］考慮國家節能減排號召，對車輛調度問題進行研究，建立碳排放成本和旅行成本最小化和配送時間最小化的雙目標模型。趙志學等［6］從綠色環保角度出發，建立車輛油耗和碳排放總成本最小和車輛運營總成本最小化的綠色車輛調度（Green Vehicle Routing Problem，GVRP）雙目標函數模型，并采用混合差分進化算法求解該模型。葛顯龍等［7］建立以車輛數最少、碳排放量最小和行駛距離最短為目標的開放式污染路徑（Open Pollution Routing Problem，OPRP）數學模型，采用改進的遺傳算法求解。Maden 等［8］使用啟發式算法求解帶時間窗車輛調度問題（Vehicle Routing Problem with Time Window，VRPTW）模型，使CO2排放減少7%。Tajik 等［9］考慮燃料消耗，以行駛距離和車輛數最小化為目標，構建帶時間窗同時取送貨污染路徑問題（Time Window Pickup-Delivery Pollution Routing Problem，TWPDPRP）數學模型。

綜上，總結近幾年相關研究，見表1，可以得到現有車輛調度相關文獻，對問題中存在的模糊需求、碳排放和同時取送貨等特性，僅考慮了其中一個或兩個，少有文獻將這些問題特性綜合考慮。同時，現有文獻在研究低碳配送問題方面，多數將碳排放問題轉化為成本的一部分，建立總成本最小的單目標模型。基于此，在考慮模糊需求、碳排放和同時取送貨的情況下，探討更為科學的低碳目標設置，即構建三個模型，模型一以運輸成本最小為目標函數、模型二以碳排放量最小為目標函數、模型三以運輸成本和碳排放成本構成的總成本最小為目標函數，同時分別記錄三種情況下的運輸成本和碳排放量，對三種模型的結果進行分析和比較。最后，提出基于2-OPT（2-OPTimization）的差分算法求解，以提高算法求解效率。

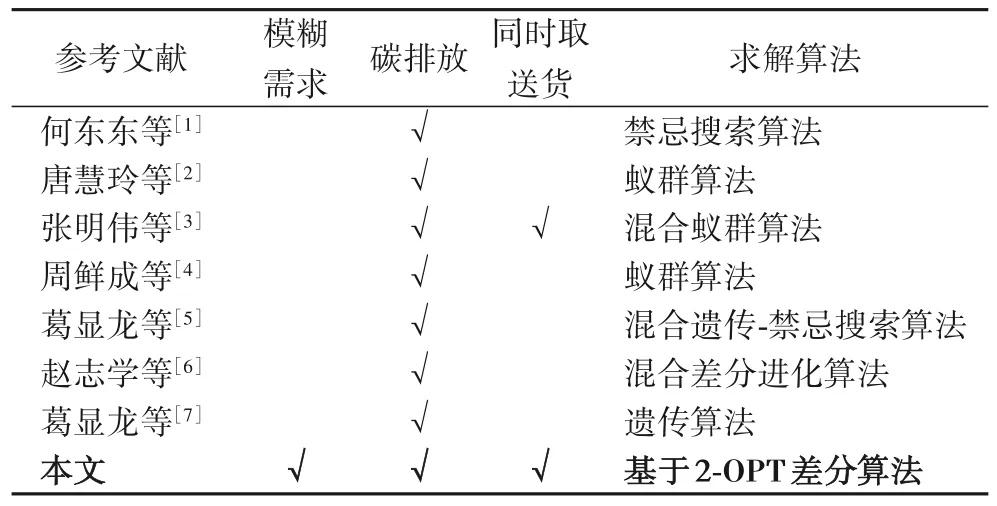
表1 關鍵文獻總結Tab.1 Summary of key literatures

1 問題描述及模型建立

對模糊需求和低碳同時取送貨問題的描述如下：整個配送網絡有一個配送中心，使用同一型號車輛對客戶進行配送作業，同時滿足各客戶的取送需求。在配送過程中，配送車輛需從配送中心出發，最終回到配送中心，且無論何時何地，配送載量不能超過車輛自身的最大載重量。模型中，考慮顧客的模糊需求和同時取送貨問題。分別建立以車輛運輸成本最小化、碳排放量最小化、以運輸成本和碳排放成本構成的綜合總成本最小的三個模型，研究三種不同目標下的同時取送貨數學模型。

1.1 期望模糊需求

近幾年，部分學者開始使用模糊理論描述車輛調度中的不確定因素。Heilpern［10］于1992 年提出模糊數概念，引入期望區間和模糊數期望值的概念。三角模糊數為解決不確定環境下的問題提供了理論基礎，避免了理論數量上的“固化”，使研究更能適應于生活中的靈活性和隨機變動性。張莉等［11］針對易腐食品供應鏈研究，因需求不確定加大了決策者的決策難度，利用三角模糊數處理外部的不確定需求，從而構建零售商決策模型。馬艷芳等［12］引入三角模糊數描述客戶需求的不確定性，建立運營成本、油耗成本和碳排放的總成本最小化為目標函數。Brito 等［13］認為行車時間和顧客需求是不確定的，并將其處理為模糊約束。

在生活中，由于各種不確定因素，在收集客戶需求信息時，只能獲取一個模糊的數據，而這些數據大多經驗所得，如“此次需求在1 至4 噸之間，最有可能的值是2.7 噸”。針對該種情況，將需求處理為模糊需求，那么將1、2.7和4分別作為三角模糊數的左邊界（即α）、中間值（即γ）和右邊界（即β），構成三角模糊數η=(α，γ，β)，其中0 ＜α≤γ≤β，其隸屬函數［10］為：

其中：α、β分別為三角模糊數的下限和上限，γ為三角模糊數最有可能的取值。

假設Z是邊fZ和gZ的模糊數η=(α，γ，β)，可以得到：

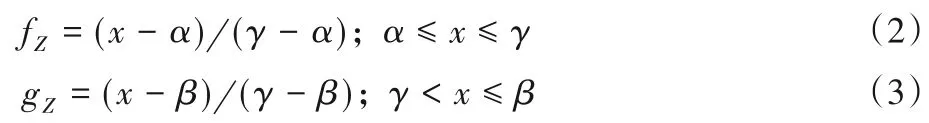
定理1［10］區間隨機集S～RI(Z)的期望值稱為模糊數Z的期望區間，用EI(Z)表示：

其中：

定理2［10］模糊成員Z的期望區間中心稱為該數的期望值，用EV(Z)表示，則有：

用一個簡單例子說明，令Z=η(1，2.7，4)，則有：

根據定理1和定理2得到：

進而求得，EI(Z)=[1.85，3.35]，EV(Z)=2.6。基于以上理論，可以獲取三角模糊數的期望值。

1.2 碳排放計算

在現實生活中，影響運輸碳排放量的因素眾多，如運輸車輛的載重量、行駛的距離、路況、車型和行駛速度等。本文采用文獻［14］碳排放計算方法，碳排放主要包含：運輸的貨物產生的二氧化碳和運輸車輛在運輸過程中自身產生的二氧化碳。具體公式如下：

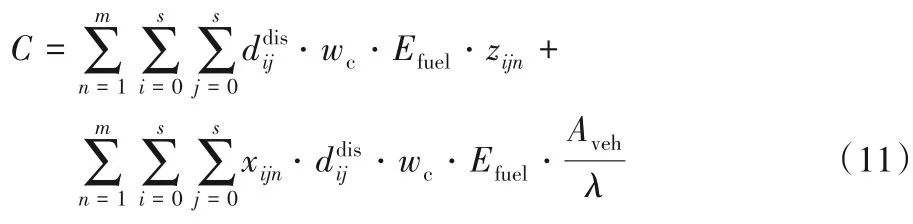
各參數取值具體如表2所示。

表2 碳排放計算相關參數Tab.2 Relevant parameters of carbon emission calculation

1.3 模型構建

模型構建所需符號如下：

Qn為車輛最大載重量；

zijn為車輛n從客戶i點到客戶j點的裝載量；

zi為車輛離開i點時的裝載量；

N為車輛的集合，N=｛1，2，…，m｝，m為最大可用車輛數；

S為節點集合，S=｛i｜i=1，2，…，s｝；其中i=0 表示物流中心，i=1，2，…，s表示客戶；

cn為車輛n行駛每公里的成本，其為變動成本；

cc為每千克二氧化碳排放費用；

W為車輛運輸成本；

C為總碳排放量；

Z為配送總成本。

基于以上理論，建立三種目標下的低碳取送貨問題模型。模型一以運輸成本最小為目標函數，如下：

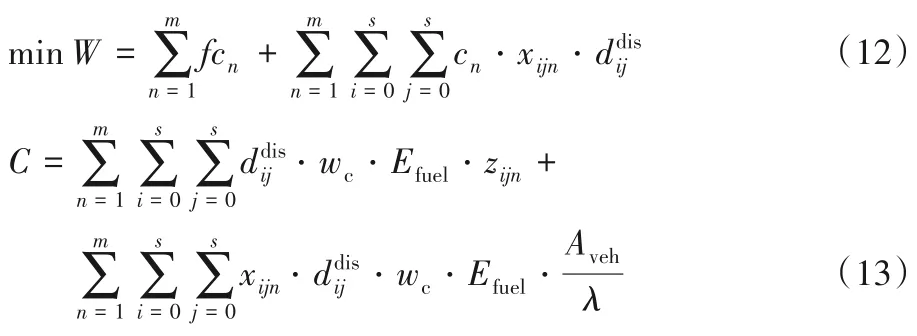
式（12）為模型一的目標函數，表示運輸成本最小化，成本共包括兩部分，一是運輸車輛的固定成本，二是運輸車輛與距離相關的變動成本。式（13）表示該模型下相應的碳排放量。

模型二以碳排放量最小為目標函數，模型如下：

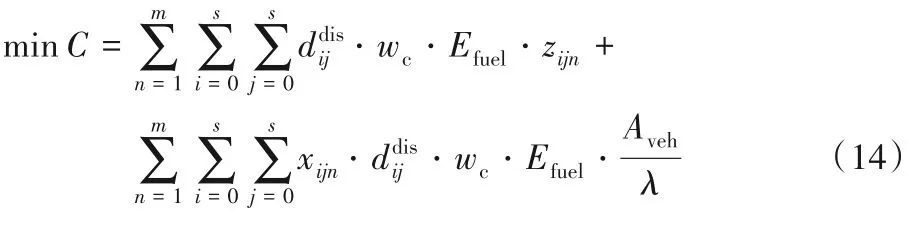
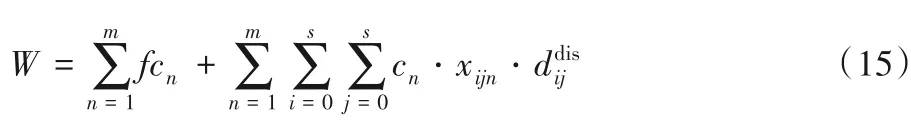
式（14）為模型二的目標函數，表示碳排放量最小化；式（15）表示該模型下相應的運輸成本。

模型三以運輸成本和碳排放成本構成的綜合總成本最小為目標函數，模型如下：

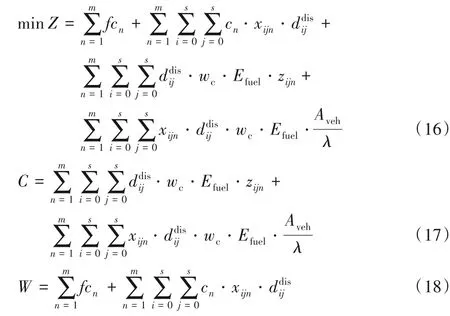
式（16）為模型三的目標數學模型，以運輸成本和碳排放成本構成的總成本最小為目標函數；式（17）和式（18）分別表示該模式下相應的碳排放量和運輸成本。以上三種模型有相同的約束，如下：

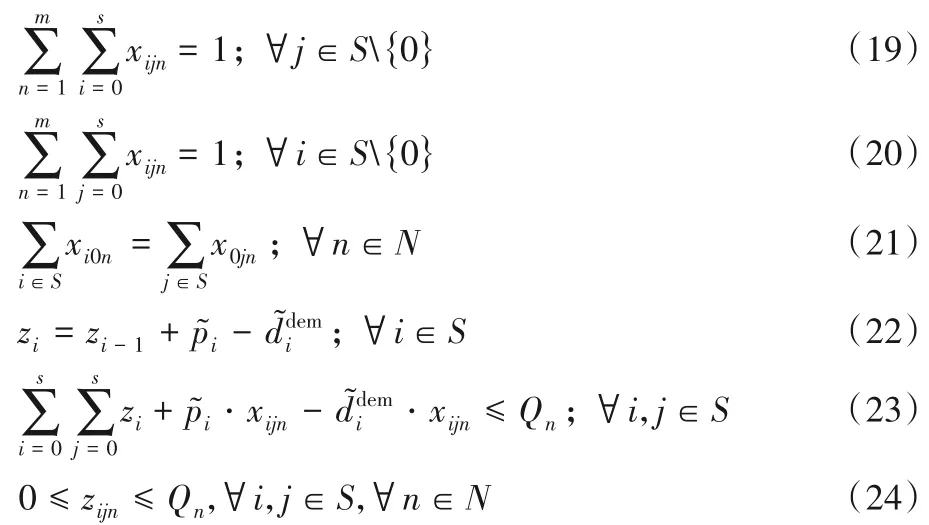
決策變量：

式（19）和式（20）表示每個客戶僅由一輛車服務；式（21）表示運輸車輛從配送中心出發，完成配送后最終回到配送中心；式（22）表示車輛離開客戶i點時的載重量；式（23）表示車輛離開客戶j點時的載重量不超過車輛的最大載重量；式（24）表示每輛車任何路段上的負載不得超過車輛最大負載限制，且非負；式（25）為決策變量。

2 差分進化算法及其改進方法

差分進化（Differential Evolution，DE）算法于1995 年由Storn 等［15］提出，是一種模擬自然界生物進化的智能算法，有較強的記憶能力，可動態調整搜索戰略；同時，還具有較好的全局收斂能力和魯棒性。在解決復雜全局優化問題時，過程更加簡單，受控參數少，被視為仿生智能計算產生以來，在算法結構方面取得的重大進展［16］。基于此，本文采用差分算法求解低碳取送貨車輛調度模型（Low Carbon Vehicle Routing Problem with Pickup and Delivery，LCVRPPD）。

2.1 個體編碼解碼

本文采用自然數編碼方式，顧客集由｛1，2，…，n｝組成，0代表配送中心。假設現有12 個顧客需要被服務，用自然數1～12 表示這12 個顧客。首次，生成的一個個體如［3，6，8，7，12，10，11，9，5，2，4，1］，然后根據各點的取送量和車載量進行編碼，同時將配送中心0 插入到隨機生成的個體后，形成一個完整的個體，如［0，3，6，8，7，0，12，10，11，0，9，5，2，0，4，1］。由此可得四輛車的配送路徑如下：

車輛1：0—3—6—8—7—0

車輛2：0—12—10—11—0

車輛3：0—9—5—2—0

車輛4：0—4—1—0

2.2 適應度函數

本文研究目標函數設置更優問題。共建立三個模型，模型一以運輸成本最小化為目標函數，同時記錄碳排放量；模型二以碳排放量最小化為目標函數，并記錄其運輸成本；模型三中，將與油耗相關的碳排放成本作為成本一部分，構建總成本最小化為目標函數，并記錄運輸成本和碳排放量。

步驟1 以運輸成本最小化為目標函數，運行算法50次，得到50 個解，并記錄這50 個解對應的碳排放量C=

適應度函數如下：

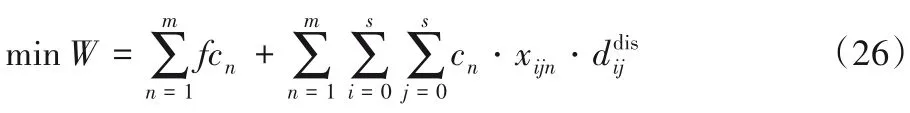
步驟2 以碳排放量最小為目標函數，運行算法50次，得到50 個解，并記錄這50 個解對應的運輸成本碳排放適應度函數如下：

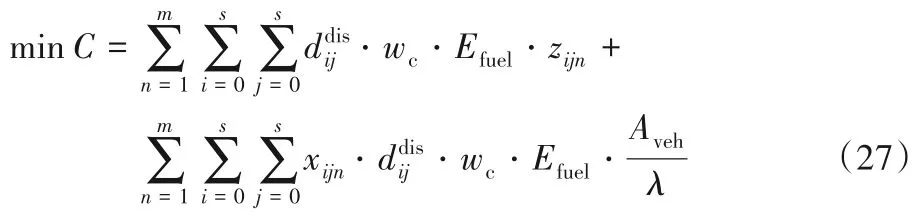
步驟3 以運輸成本和碳排放成本構成的總成本最小為目標函數，運行算法50次，得到50個解，并記錄對應的運輸成本和碳排放量C=適應度函數如下：

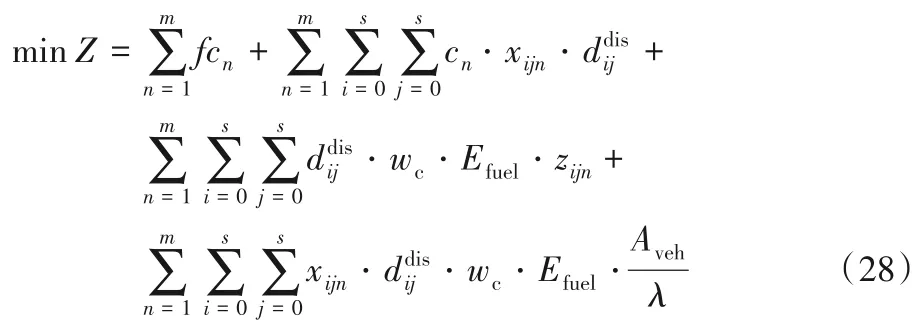
2.3 基于DE的更新操作

基于2-OPT 的變異算子。雖然差分演化算法具有結構簡單、使用簡單和魯棒性好等特點，但同時也存在一定的缺點，在求解全局最優解時收斂慢，并且容陷入局部最優解。基于此，提出基于2-OPT 的差分算法。2-OPT 是局部搜索算法中的一種，工作原理是先求得一個解，將所得解的兩條邊進行交換然后求解得到一個新解。將新解和原解比較，擇優淘劣。通過引入2-OPT算法，用新的變異方法取代DE 自身的變異機制，提高DE 的收斂速度。基于2-OPT 的差分算法變異操作［17-18］如下：

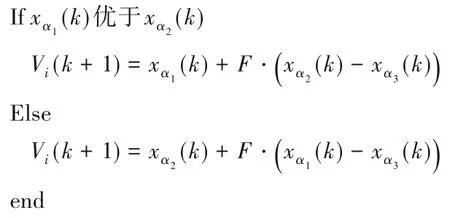
本文F設置為0.5［19-21］。簡單舉例：現對8 個顧客點，3 輛車，隨機選出的3 個個體進行變異操作。其中3 個個體分別為：X1（1，3，5，0，8，2，0，4，0，6，7）、X2（3，0，5，7，0，4，1，0，2，8，6）、X3（8，5，0，3，2，1，0，6，0，7，4），具體變異過程如圖1所示。

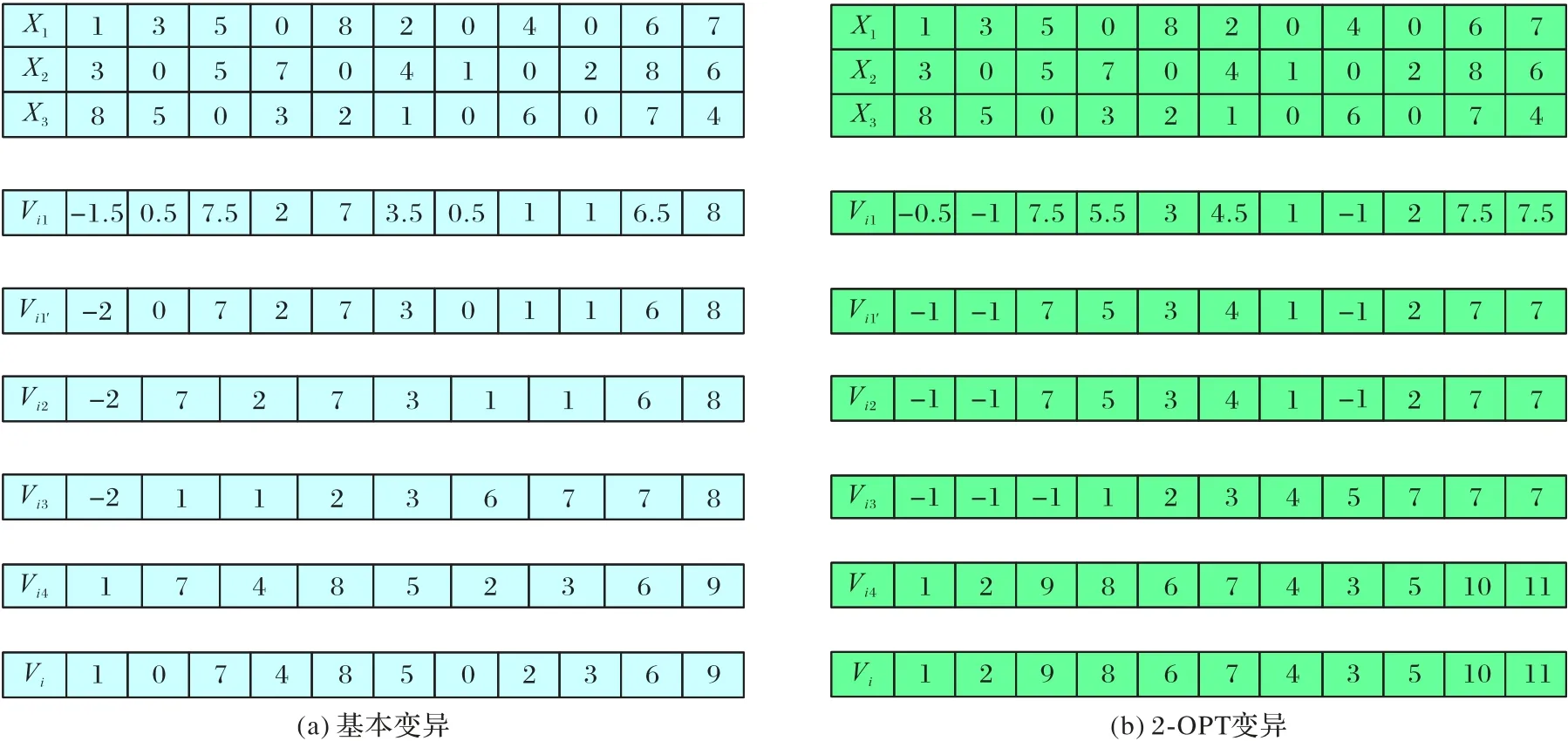
圖1 變異操作Fig.1 Mutation operation

處理過程具體如下（兩種方法僅計算公式不同，其他步驟均相同）：

1）對8 個顧客點、3 輛車以及隨機選出的3 個個體X1（1，3，5，0，8，2，0，4，0，6，7）、X2（3，0，5，7，0，4，1，0，2，8，6）、X3（8，5，0，3，2，1，0，6，0，7，4）進行變異及處理。

基本變異公式為：

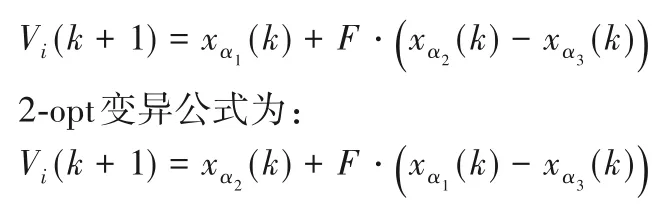
2）通過基本公式求得Vi1（-1.5，0.5，7.5，2，7，3.5，0.5，1，1，6.5，8），對其取整得到Vi1'（-2，0，7，2，7，3，0，1，1，6，8）。

3）提取Vi1'中0 并記錄其所處的位置（0 的位置為2 和7）。當0 的個數超過車輛數時，只提取車輛數個0，得到Vi2（-2，7，2，7，3，1，1，6，8）。

4）將Vi2按照從小到大的順序排列，得到Vi3（-2，1，1，2，3，6，7，7，8）。

5）用序號代替原編碼值。例如Vi2中的-2 在Vi3中為第1位，則在Vi4中相應的位置填1；Vi2中的2 在Vi3中為第4 位，則在Vi4中相應的位置填4；依次得到Vi4（1，7，4，8，5，2，3，6，9）。

6）將步驟1）取出的0插入到原來的位置，得到Vi（1，0，7，4，8，5，0，2，3，6，9）。

二項交叉算子。交叉一般分為指數交叉和二項式交叉。父代和子代種群間交叉使用二項交叉更為有效，可充分利用各代種群間的信息，從而加速算法進行。基于此，本文采用二項交叉，具體見圖2。

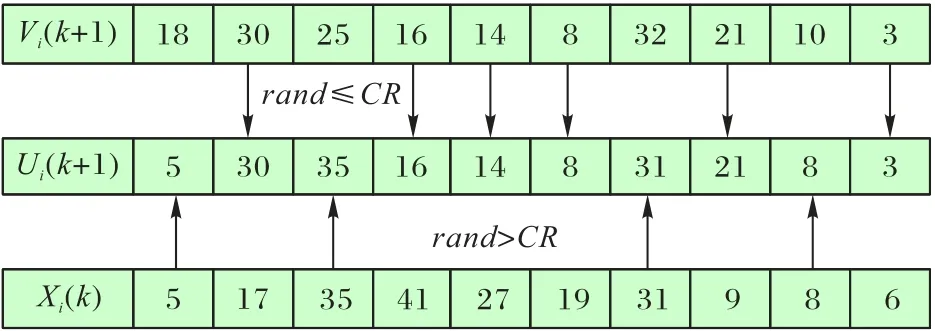
圖2 交叉操作Fig.2 Crossover operation

貪婪選擇算子。如果實驗體的適應度值比目標個體的適應值更優異，則在下一代過程中實驗體將取代目標個體，作為新的目標個體；否則，保持原有的目標個體。

該算法的總體流程如圖3所示。

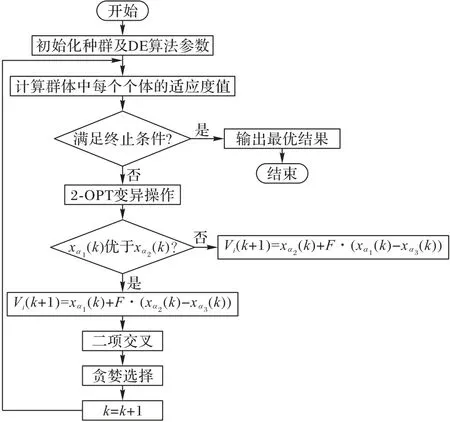
圖3 總體流程Fig.3 Overall flowchart

3 案例研究

在案例研究部分，首先采用田口法確定相關參數最適合取值，在最佳取值情況下，對三種不同目標模型的運輸成本和碳排放量進行比較，并對其進行相關性分析。最后將基本遺傳算法（Genetic Algorithm，GA）、基本粒子群優化（Particle Swarm Optimization，PSO）算法和提出的基于2-OPT 的差分進化（Differential Evolution based on 2-OPT，DE-2OPT）算法對比，驗證算法的有效性和合理性。所有啟發式方法在計算機上使用Matlab R2012a 執行的，其帶有AMD E1-1500 APU with Radeon（tm）HD Graphics 處理器，Windows 7旗艦版32位操作系統。案例中，Matlab 隨機生成28個顧客服務點，考慮用6輛車輛配送，每輛車的載重量為10 t，每輛車的固定成本為300元，變動成本2 元/km，每升柴油5.8 元，整車質量為6.2 t，碳排放價格0.6 元/kg。假設配送中心位置為原點，28 個客戶的坐標位置及模糊需求如表3所示。

表3 顧客相關信息Tab.3 Customer information

3.1 算法參數田口分析

田口分析法首次將產品設計思想和穩健性相結合，將噪聲參數對系統的影響引入實驗中，并通過實驗找出最佳水平的組合。田口分析的函數共分為3 類，分別是望目特性的質量函數、望小特性的質量函數及望大特性的質量函數。本文目標函數是運輸成本最小化和碳排放最小化，所以選擇望小特性的質量函數。

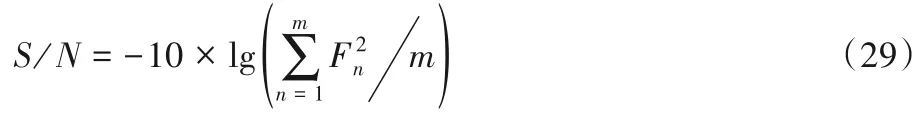
其中：m是不同參數組合運行的次數；F是響應函數值，即目標函數值；Fn是第n次的實驗目標函數值。

算法效果對算法參數設置很敏感，不同參數設置影響算法的有效性。為探討種群大小和迭代次數對算法的影響，將交叉常數CR（Cross）設置為0.9，縮放因子F設置為0.5，種群大小NP（Number of Population）分別設定為10、20、30、40、50，迭代次數分別為100、200、300、400、500，一共組成25個組合。選擇的是L25（5*2）的水平用MINITAB 軟件進行田口分析，分析結果見表4。

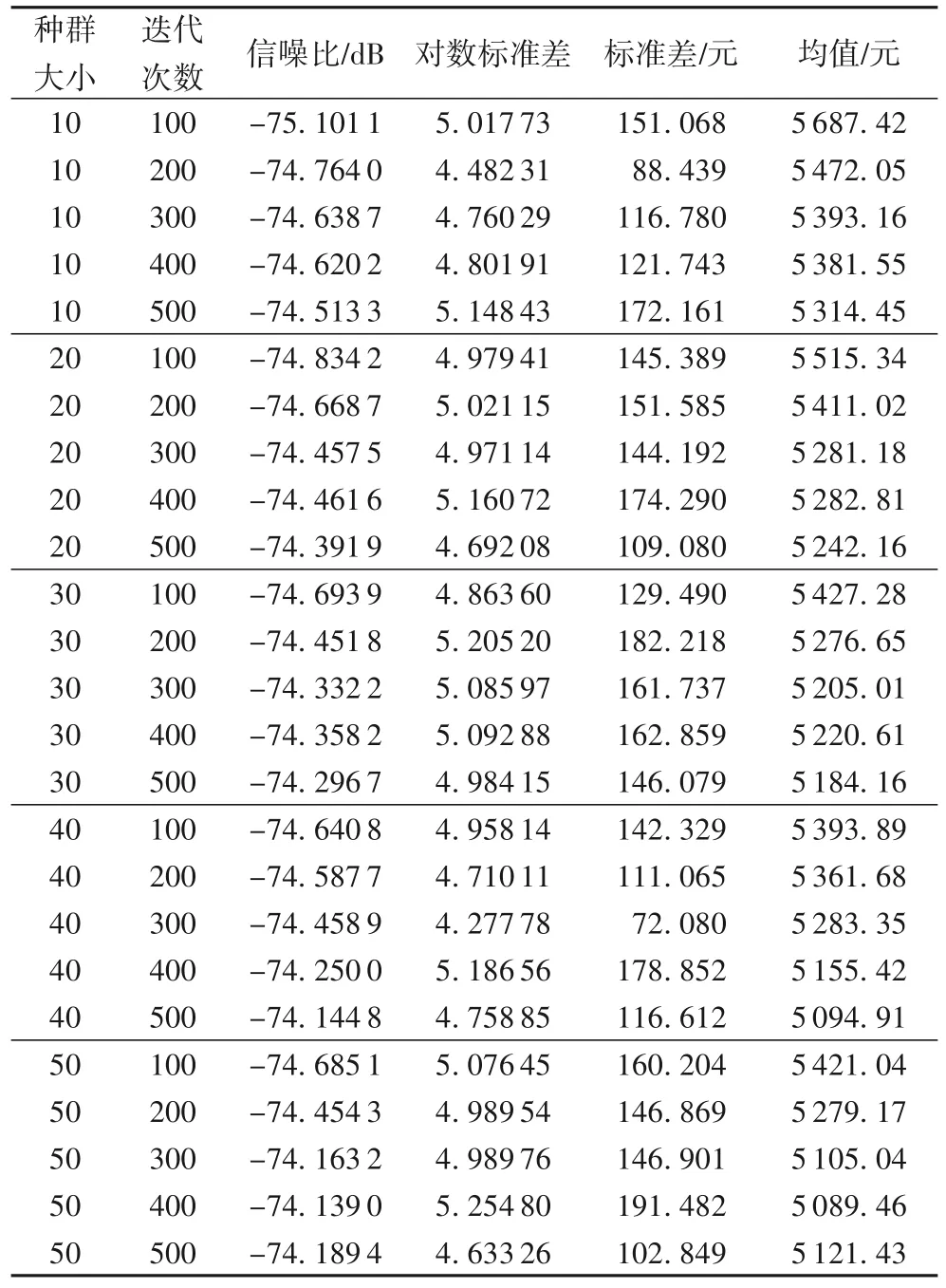
表4 田口分析Tab.4 Taguchi analysis

圖4中，當種群大小NP=50，迭代次數為400時，信噪比最大（田口方法任何時候都是信噪比越大越好。圖4 左下角的橫坐標為種群大小，縱坐標為信噪比，當種群大小NP=50 時，信噪比數值最大；右上角的橫坐標為迭代次數，縱坐標為信噪比，當迭代次數為400 時，信噪比數值最大。綜上，當NP=50，迭代次數為400時，信噪比最大）。圖5表示當種群為NP=50，迭代次數為400 時，均值最小（目標函數為最小化，均值則取最小值。圖5 左下角的橫坐標為種群大小，縱坐標為成本（單位：元），當NP=50時，成本最小；右上角的橫坐標為迭代次數，縱坐標為成本（單位：元），當迭代次數為400 時，成本最小。綜上，當種群為50，迭代次數為400 時，均值最小）。因此，根據田口分析法，設置種群大小為50，迭代次數為400。

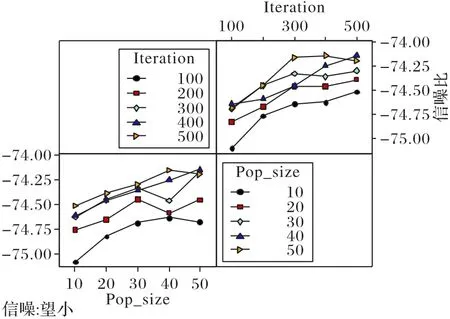
圖4 信噪比交互作用圖Fig.4 Signal-to-noise ratio interaction diagram

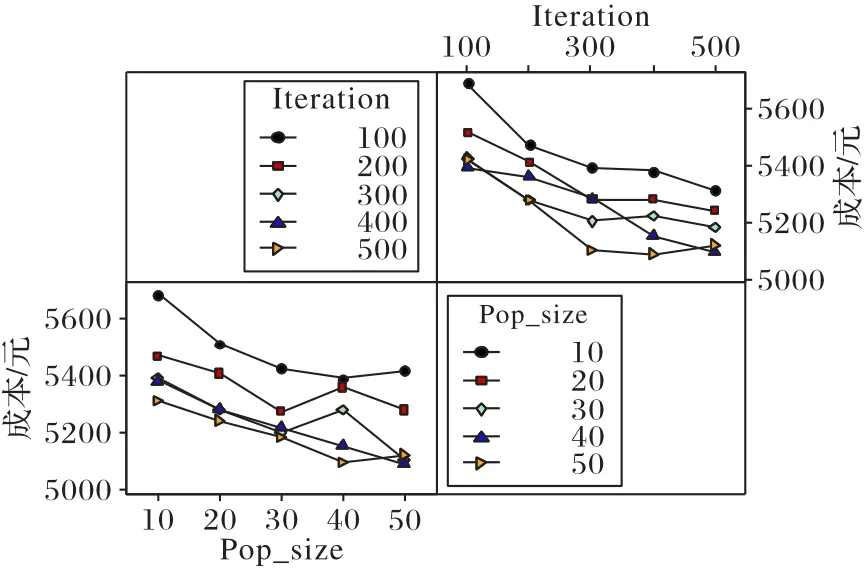
圖5 成本均值交互作用圖Fig.5 Cost mean interaction diagram

3.2 模型對比分析

根據田口法分析結果，種群大小設置為50，迭代次數為400。首先按2.2 節中適應度函數將三個不同目標模型分別運行50 次，記錄50 個解對應的碳排放量和運輸成本，散點圖如圖6所示。圖6表明，三種模型下的運輸成本和碳排放量均趨于正相關。因此，本文采用一款統計分析軟件SPSS（Statistical Product and Service Solutions）對數據進行相關性分析，具體分析結果如表5和表6所示。

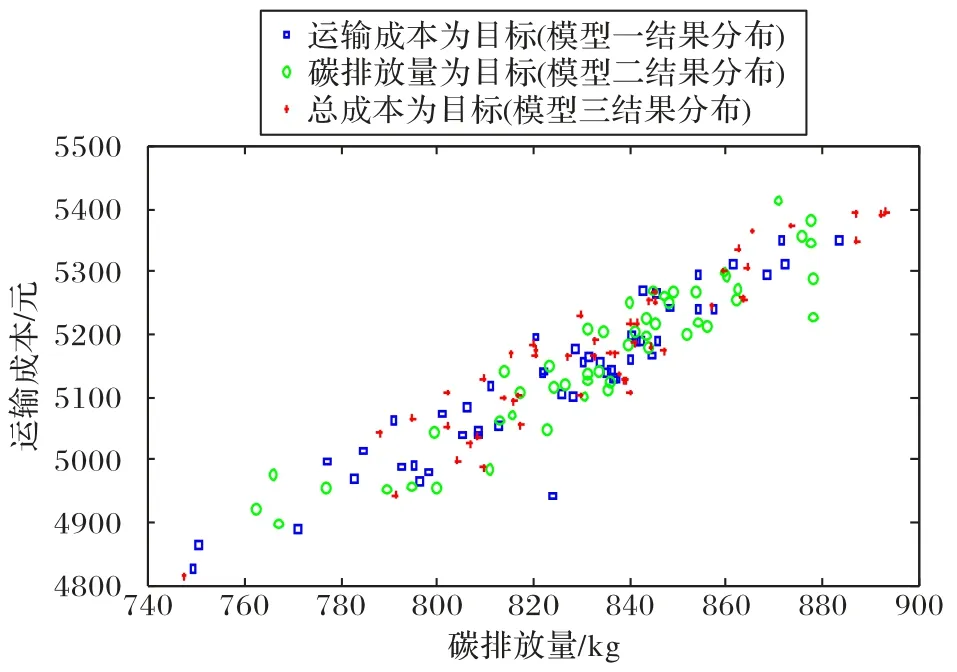
圖6 不同目標下碳排放量和運輸成本分布Fig.6 Distribution of carbon emission and transport cost under different objectives

由表5 的模型一可得，當運輸成本最小為目標函數時，運輸成本和碳排放量的相關性系數為0.928；由表5的模型二可得，當碳排放量最小為目標函數時，運輸成本和碳排放量的相關性系數為0.932；由表5 的模型三可得，當總成本為目標函數時，運輸成本和碳排放量的相關性系數為0.859。

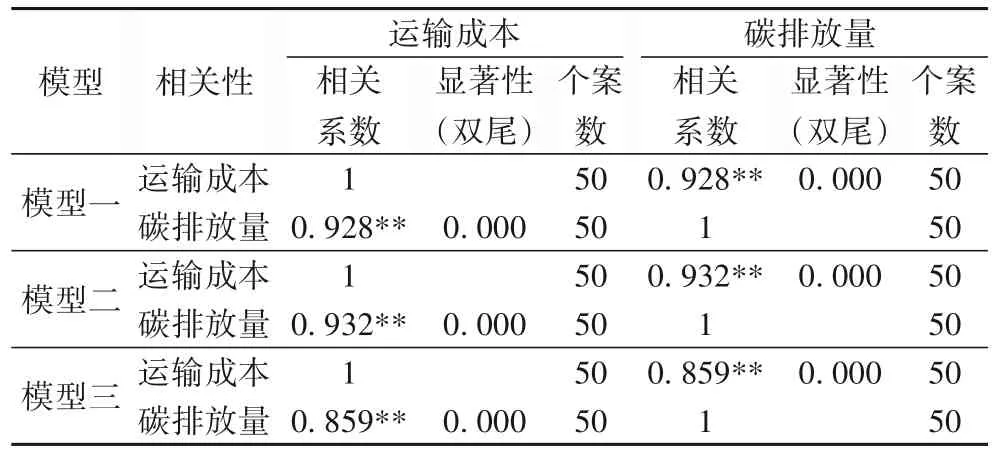
表5 三種模型下運輸成本與碳排放量相關性分析Tab.5 Correlation analysis between transportation cost and carbon emission under three models

表6 是三種模型下150 組運輸成本和碳排放量的相關性分析，相關性系數為0.920。以上相關性系數均在0.01級別，相關性顯著。表6 表明運輸成本和碳排放量相關性很高，為進一步探討將目標函數設置合理性問題，將三種模型所對應的運輸成本和碳排放量進行對比分析，見表7。

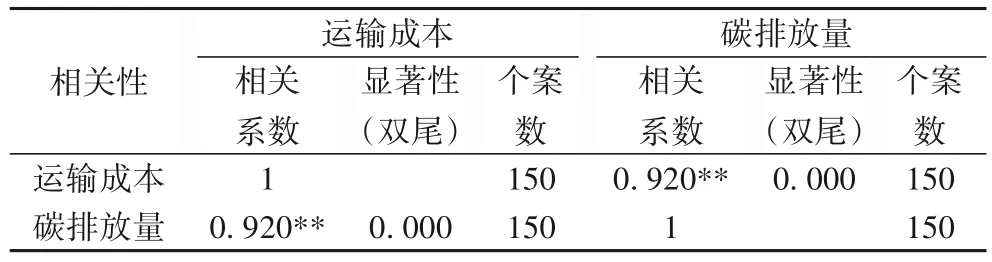
表6 總體的運輸成本和碳排放量相關性分析Tab.6 Overall correlation analysis of transportation cost and carbon emission

運輸成本最小為目標函數時，平均運輸成本為5 127.66元，平均碳排放量為824.38 kg；碳排放量最小為目標函數時，平均運輸成本為5 165.42 元，平均碳排放量為833.70 kg；總成本為目標函數時，平均運輸成本為5 126.47元，平均碳排放量為822.42 kg。三個不同目標函數的運輸成本方差分別為15 896.65 元2、15 634.52 元2和8 939.99 元2，碳排放量方差分別為915.07 kg2、864.33 kg2和479.85 kg2。綜上，碳排放量與運輸成本呈正相關關系，而以構建總成本最小的LCVRPPD模型，其對應解的效果更好。

表7 三種目標模型解的對比Tab.7 Comparison of solutions of three models with different objective functions

3.3 算法對比分析

為進一步驗證該算法的有效性和合理性，本文將針對3種不同客戶規模分別采用差分進化算法（DE）、基本遺傳算法（GA）、基本粒子群優化（PSO）算法和提出的基于2-OPT 的差分算法（DE-2OPT）進行求解，并對比其計算結果。相應參數如表8所示，其中：NP為種群大小，G為迭代次數，W為學習因子，R為變異概率，C為交叉概率，CR為交叉常數，F為縮放因子。

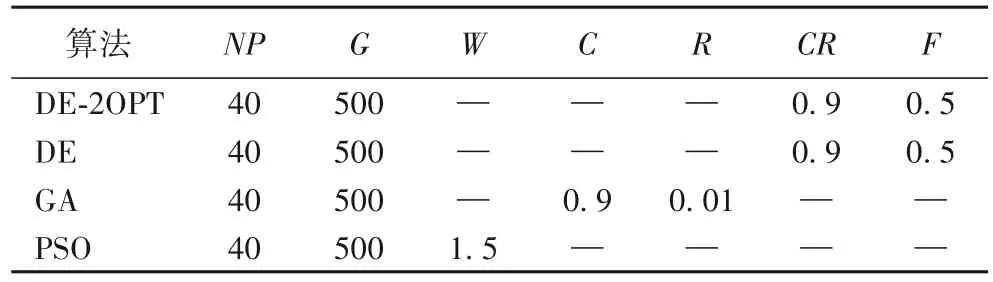
表8 各算法對應參數Tab.8 Corresponding parameters of different algorithms

將客戶分為25、50 和75 個三種規模，并將各算法分別運行20次，分別取各算法最優解。計算結果如表9所示，算法迭代效果圖如圖7所示。由表9可以得出，本文提出的算法求解結果優于差分進化算法、傳統遺傳算法和粒子群優化算法。當客戶數量為25 時，與差分進化算法相比，本文提出算法的總成本降低1.8%，碳排放量降低0.7%；與遺傳算法相比，本文提出算法的總成本降低1.9%，碳排放量降低1.2%；與粒子群優化算法相比，本文提出算法的總成本降低4.0%，碳排放量降低1.56%。

當客戶數量為50 時，從表9 可看出，與差分進化算法相比，本文提出算法的總成本降低1.75%，碳排放量降低2.9%；與遺傳算法相比，本文提出算法的總成本降低4.2%，碳排放量降低6.5%；與粒子群優化算法相比，本文提出算法的總成本降低4.8%，碳排放量降低14.35%。

當客戶數量為75 時，從表9 可得出，與差分進化算法相比，本文提出算法的總成本降低3.0%，碳排放量降低3.5%；與遺傳算法相比，本文提出算法的總成本降低16.47%，碳排放量降低4.3%；與粒子群優化算法相比，本文提出算法的總成本降低22.5%，碳排放量降低7.88%。

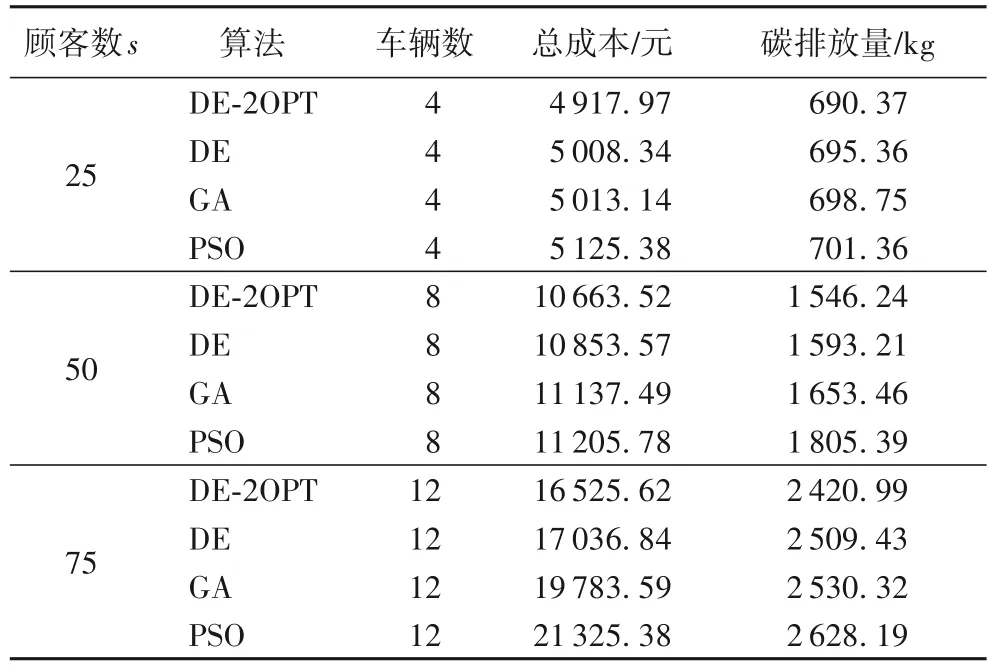
表9 不同規模客戶四種算法結果對比Tab.9 Comparison of results of four algorithms for customers with different scales

由圖7 可以得到，隨迭代次數的增加，解趨向于穩定并且越來越優。其中可以看出：GA計算時間長、收斂慢，但是其求解效果好，全局尋優能力強；PSO 算法易陷入局部最優解，挖掘能力較差，求解時間短；DE算法收斂快，但較易受種群個體大小的影響；DE-2OPT算法有較好的全局收斂能力和魯棒性，收斂較快。故而，認為DE-2OPT 對于求解所提出的模型是有效的。

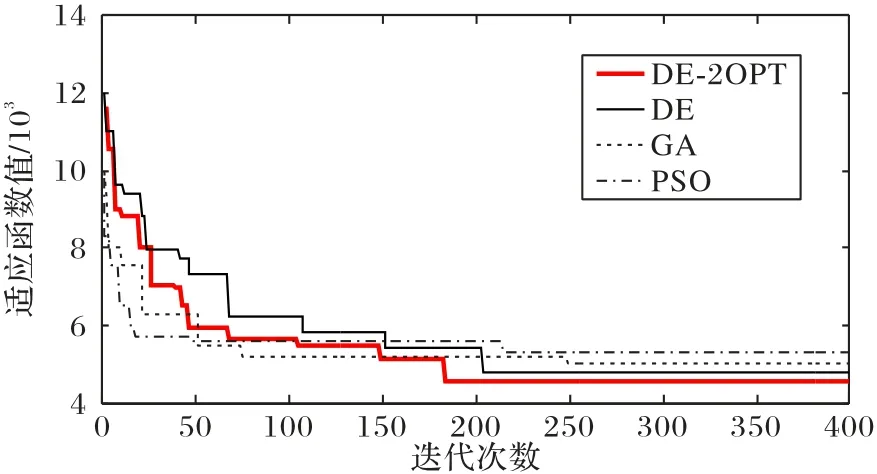
圖7 算法迭代對比Fig.7 Algorithm iteration comparison

4 結語

本文基于模糊需求下同時取送貨問題，研究探討低碳目標函數設置問題，分為三種情況：一是以運輸成本最小、二是以碳排放量最小、三是由運輸費用和碳排放費用構成的總成本最低。隨后，提出基于2-OPT 的差分進化算法求解模型。案例研究中，首先采用田口法獲取相關參數的合理取值。隨后通過SPSS 分析得出：當運輸成本最小為目標函數時，運輸成本和碳排放量的相關性系數為0.928；當碳排放量最小為目標函數時，運輸成本和碳排放量的相關性系數為0.932；當總成本最小為目標函數時，運輸成本和碳排放量的相關性系數為0.859。同時分析三個目標函數下150 組運輸成本和碳排放量的相關性，其相關性系數為0.920。

因運輸成本和碳排放量相關性顯著，為進一步探討將目標函數設置合理性問題，將三種模型所對應的運輸成本和碳排放量進行對比分析。運輸成本最小為目標函數時，平均運輸成本為5 127.66 元，平均碳排放量為824.38 kg；碳排放量最小為目標函數時，平均運輸成本為5 165.42元，平均碳排放量為833.70 kg；總成本為目標函數時，平均運輸成本為5 126.47 元，平均碳排放量為822.42 kg。3 個不同目標函數的運輸成本方差分別為15 896.65、15 634.52 和8 939.99，碳排放量方差分別為915.07、864.33 和479.85，總成本最小為目標函數時穩定性最好。

綜上，碳排放量與運輸成本呈正相關關系，同時構建總成本最小的LCVRPPD 模型，其對應解的效果更好。最后對DE-2OPT、DE、GA 和PSO 四種算法進行對比，驗證該算法的有效性及合理性。本研究仍存在一些不足，例如沒有考慮天氣、不同車型以及顧客的滿意度對運輸過程的影響，這些將是進一步研究的方向。