基于改進Dijkstra算法的AGV路徑規劃研究*
李全勇,李 波,張 瑞,姜 濤
(1.內蒙古一機集團力克橡塑制品有限公司 技術中心,內蒙古 包頭 014000;2.湖北文理學院 機械工程學院,湖北 襄陽 441053;3.武漢科技大學 機械自動化學院,湖北 武漢 430081;4.北京星航機電裝備有限公司 技術中心,北京 100071)
0 引言
自動導航運輸車(AGV)作為智能物流的核心設備,廣泛應用于汽車、食品、煙草、醫療、服裝等行業。路徑規劃是AGV應用的核心技術之一,對其進行研究具有極高的工程價值。文獻[1]提出了一種基于時間最短的無碰撞路徑算法;文獻[2]在AGV調度算法中計入空閑時間,基于遺傳算法進行調度規劃;文獻[3]將改進遺傳算法應用于AGV避障路徑規劃;文獻[4]研究了細菌勢場算法,求解移動機器人靜態和動態路徑規劃;文獻[5]在車間調度中引入了灰狼優化算法,預測工件到達時間;文獻[6]提出了改進重力搜索算法,仿真實現了在靜態障礙物下的路徑規劃;文獻[7]采用Dijkstra算法求解單臺AGV最短路徑,實現AGV的智能無線控制;文獻[8]提出一種改進型蟻群路徑規劃算法,加入全局信息素更新機制,提高了算法的搜索效率;文獻[9]以最小化最大搬運完成時間為目標,研究了一種生成無路徑沖突的路徑規劃算法;文獻[10]采用遺傳算法對改進蟻群算法進行參數優化,以提高收斂速度,避免局部最優。
針對磁導AGV運行特點,本文進行了基于柵格法的拓撲地圖建模,分析了A*、蟻群、遺傳、Dijkstra算法的AGV路徑規劃問題,引入路徑平滑度,并以時間權重為優化目標求解最優路徑,提出了改進Dijkstra算法,開發了路徑規劃仿真系統,進行了多種算法AGV路徑規劃對比分析。
1 AGV地圖模型構建
地圖模型構建是AGV路徑規劃的基礎,直接影響路徑規劃算法的設計。本文基于柵格法的無向有權拓撲地圖方法,開展AGV運行環境的建模,如圖1所示。

圖1 地圖建模
以柵格圖為基礎,每個網格中心為節點,連接相關節點作為邊,其代表路徑規劃中的磁導線。保留圖中節點和邊,去除網格,剩下部分為拓撲地圖的地圖模型。
2 基于改進Dijkstra算法的AGV路徑規劃
針對拓撲圖下的AGV路徑規劃問題,A*算法求解最短路徑,但由于受到估計代價值的影響,算法出現局部最優,穩定性不佳;蟻群算法雖能得到強魯棒性的優化路徑,但對全局搜索能力較低,收斂速度較慢,容易在搜索過程中陷入局部最優;遺傳算法具有良好的搜索能力,不易陷入局部最優,但局部搜索能力較差,進化后期搜索效率較低,需對算法本身參數進行優化,避免過早收斂。
Dijkstra算法[11]作為一種貪心算法,以起始點為中心源點層層向外擴散直至搜索到所有節點的最短路徑。其根據路徑總權重來獲得最短路徑,兩節點之間權重使用一般直線距離公式求解:
(1)
傳統Dijkstra算法作為典型的最短路徑算法,可準確獲取全局最優路徑,通常將路徑長度作為權重因子搜索最短路徑,但無法考慮到路徑平滑度對AGV實際運行中的影響。
本文提出以時間權重作為最優路徑的考慮因素,通過模擬AGV從起點至終點運行花費的總時長,對比AGV在各個可行路徑中的運行最短時長,篩選出最優路徑。時間權重T函數表達式為:
(2)
其中:Dij為節點i、j之間的距離;U為AGV在路徑直線部分的平均速度;TΦ為彎道總權重,表示AGV經過所有彎道時間權重;Tij為時間總權重,表示AGV從節點i到節點j總權重。彎道總權重函數表達式為:
(3)
其中:S(i,i+1)為首尾分別為節點i與節點i+1的邊;tΦ為兩條相鄰邊夾角的權重。
AGV在巡線過程中面對不同角度彎道做出不同動作,其中夾角權重如式(4)所示:
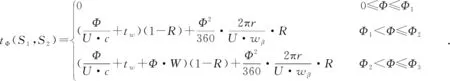
(4)
其中:R為拐彎類型標識符,R=0表示角度彎,R=1表示為弧度彎;r為拐彎半徑;c為轉彎因子,根據不同AGV拐彎機制設定,值為常量,用U·c表示AGV拐彎角速度;wβ為減速因子,用于弧度彎道中,表示AGV過彎時減速程度;W為旋轉精度懲罰因子;Φ為轉角角度;tw為減速損耗權重,用于表示減速帶來的時間損耗,表達函數為:
(5)
其中:dw為減速緩沖距離(減速節點與轉彎節點的距離);wα為減速因子,表示AGV進入彎道前的減速程度,wα≤1。
AGV經過不同角度彎道時會產生不同層次時間損耗,根據這一特性,依據角度Φ的不同,將夾角權重tΦ分為三個階段分析求解:
第一階段(0≤Φ≤Φ1):轉彎夾角很小,此類彎道所產生時間損耗為0。
第二階段(Φ1<Φ≤Φ2):彎道夾角適中,AGV無法通過自動巡線功能通過此類彎道,可在彎道夾角放置拐角節點,根據信號依次完成急停、準確地旋轉相應角度、恢復巡線速度等動作。
第三階段(Φ2<Φ≤Φ3):當彎道夾角過大,AGV無法旋轉至相應角度,會產生或多或少的旋轉角度誤差。此時,AGV會通過自身巡線功能,以拐角節點為中心左右旋轉尋找磁導線。隨著拐彎夾角的增大,產生的誤差角度也會增大,隨之帶來的巡線損耗時間也會增加。為此提出W旋轉精度懲罰因子,可根據不同AGV自身的性能設值。
通過對兩夾角的權重分析,最優路徑權重可由式(6)表示:
(6)
3 仿真驗證
采用C#語言開發了Winform應用程序,進行了多算法仿真實驗。圖2為AGV仿真平臺界面截圖,采用柵格法拓撲圖進行車間地圖布局。
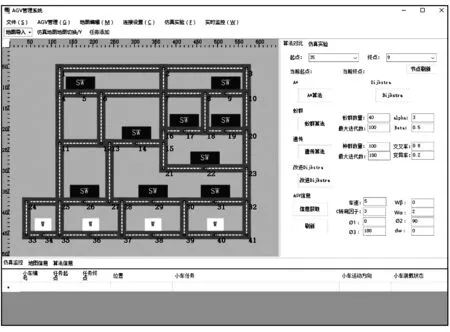
圖2 仿真界面
根據圖1地圖模型,將41個節點與53條邊信息錄入系統,完成實驗數據初始化。地圖拐角信息主要采用角度彎道,U=5(以模型比例設置),wα=2,wβ=0,Φ1=0°,Φ2=90°,Φ3=180°,c=3°,dw=10,W=0。通過選擇不同任務起點與終點進行實驗,結果如表1所示。
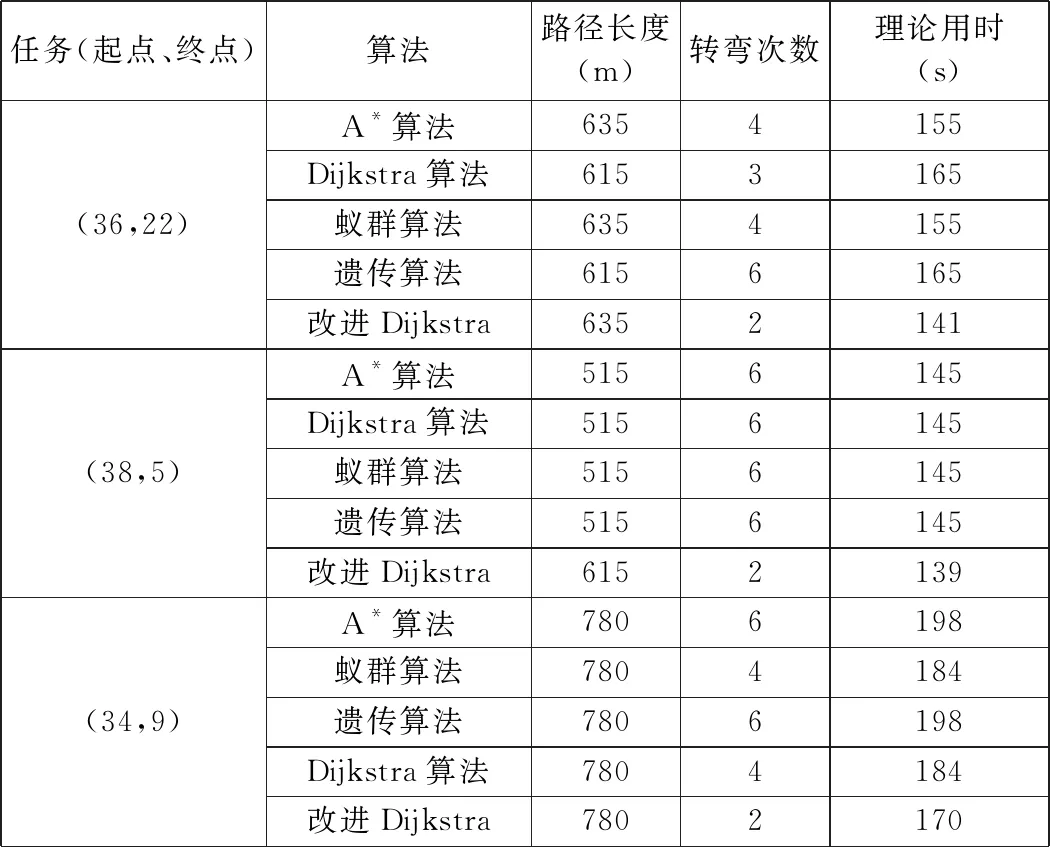
表1 實驗數據表
通過多次實驗,選擇三組特征值最明顯的數組進行對比,主要結論如下:
(1) 蟻群算法與遺傳算法在求取最優路徑時具有不穩定性,在多次求解過程中會出現多個長度相同、但是拐彎次數不同的路徑,在迭代次數不足的情況下,蟻群算法更是無法獲取路徑長度最短的解。
(2) A*算法、遺傳算法、改進Dijkstra算法的穩定性更好。
(3) 改進Dijkstra算法每次獲取路徑都為最優解(理論用時最短),求得路徑長度雖大于其他路徑算法,但理論用時依然是最少。
為進一步驗證算法的可靠度,開展了120個節點車間環境的仿真實驗,布局如圖3所示。

圖3 地圖模型
120個節點使用了無規律的連接來降低實驗環境的平滑度,總共有173條連接線。仿真實驗以1號節點為起點,選擇圖中一系列坐標點作為實驗終點進行多次驗證。
采用蟻群算法與遺傳算法分別對每組數據進行100次實驗并提取平均值,進行實驗數據對比。其中蟻群算法參數設置為:蟻群數量40,最大迭代次數40,alpha=3,beta=0.5;遺傳算法參數為:染色體數量50,最大迭代次數20,最大變異次數20,交叉率0.8,變異率0.2。實驗數據對比如圖4所示。
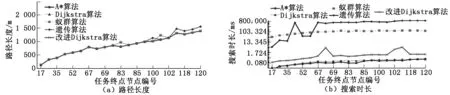
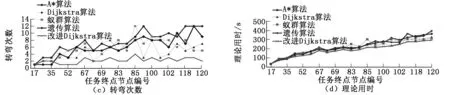
圖4 仿真數據對比
4 結語
本文基于柵格的無向有權拓撲方法,建立了AGV系統仿真地圖模型;分析了A*、蟻群、遺傳和Dijkstra算法,針對上述算法在拓撲圖中的適用性問題,提出了改進的Dijkstra算法,引入路徑平滑度,以時間權重為優化目標求解最優路徑;基于仿真平臺,開展了上述算法在拓撲地圖模型的實驗對比,測試結果表明:改進Dijkstra算法在路徑拐彎次數、模擬運行時間等方面具有良好表現。

