關于對角互補四邊形模型的探究與思考
施德儀


[摘 ?要] 對角互補四邊形模型是初中重要的幾何模型,該模型總體上可分為兩大類型,即90°的對角互補模型和120°的對角互補模型. 利用模型特性可推得關于角平分、線段關系和幾何面積等的一些結論以及模型中的四個頂點共圓. 文章將深入解讀模型,結合實例應用模型,并對模型進行拓展探究,從而提出相應的教學建議.
[關鍵詞] 對角互補;四邊形;模型;旋轉;四點共圓
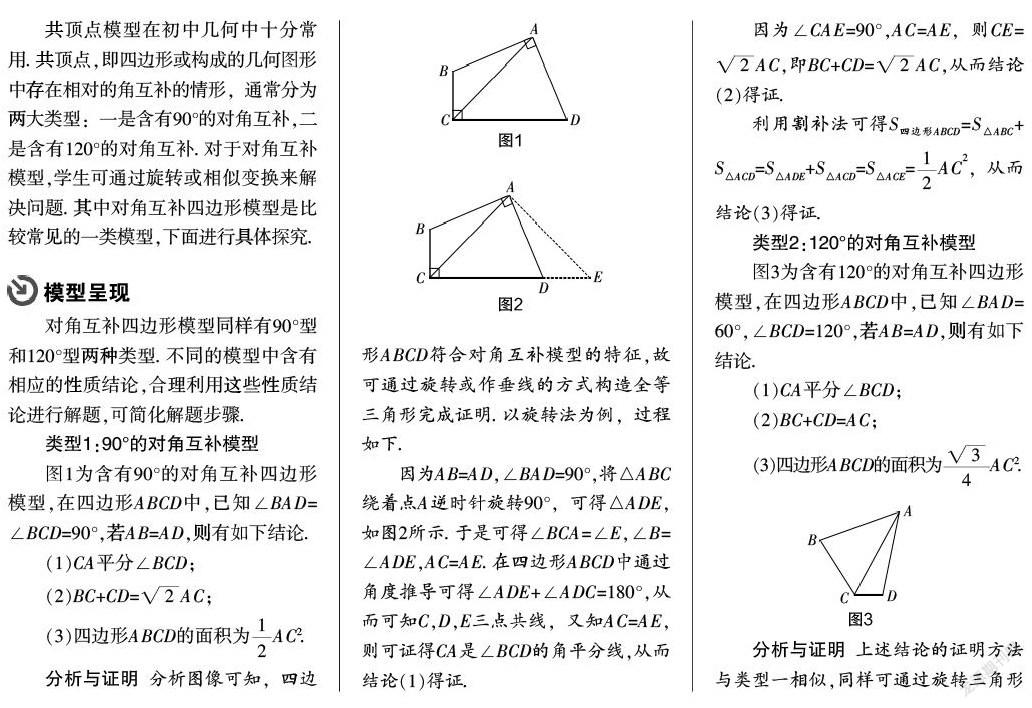
共頂點模型在初中幾何中十分常用. 共頂點,即四邊形或構成的幾何圖形中存在相對的角互補的情形,通常分為兩大類型:一是含有90°的對角互補,二是含有120°的對角互補. 對于對角互補模型,學生可通過旋轉或相似變換來解決問題. 其中對角互補四邊形模型是比較常見的一類模型,下面進行具體探究.
模型呈現
對角互補四邊形模型同樣有90°型和120°型兩種類型. 不同的模型中含有相應的性質結論,合理利用這些性質結論進行解題,可簡化解題步驟.
分析:由圖像可知,四邊形CDEF為對角互補四邊形,由其性質可知,四點位于同一圓上,故可作其外接圓,借助圓周角定理來推導相關的角度條件.
解:矩形ABCD中,已知∠BAE=∠CDE=90°,AB=CD,又知BE⊥AC,則C,D,E,F四點均在以CE為直徑的圓上,故可作出該圓,如圖11所示,可推知∠CED=∠CFD. 利用條件可證△ABE≌△DCE,所以∠DEC=∠AEB,利用角度推導可得∠AEB=∠DCF=∠DEC=∠DFC,所以DF=DC.
評析 ?對角互補四邊形的頂點共圓是該模型的顯著特征,模型中隱含了圓的幾何性質,充分利用圓周角定理可推導相關角度的大小. 解題時可以按照“提煉模型→構建輔助圓→圓性質推導”的思路進行建模和解析.
解后反思
1. 深入探究模型,研讀模型性質
對角互補四邊形模型在初中幾何中十分重要,有著極高的研究價值,探究過程要關注模型的知識背景,總結模型的解析策略及性質特征. 對角互補四邊形模型中融合了角平分線、垂直平分線、幾何旋轉,其中隱含了角平分線的性質定理、垂直平分線的性質定理以及三角形全等等知識. 在探究過程中,教師要引導學生借助全等來推導角和邊長的關系. 教學中建議采用“模型解讀→性質總結→應用強化”的思路逐步探究模型,認識模型的性質,完成從“知識認知”到“知識應用”的過渡.
2. 倡導模型拓展,循序引導教學
開展模型探究要遵循循序漸進、由淺入深的原則,同時注重模型拓展. 以上述對角互補四邊形模型為例,教學中除了要注重模型的基本特征、性質講解外,還應合理地拓展模型,如四邊形的四點共圓,可增設一些鋪墊式的問題,引出四邊形的隱圓,合理設問引導學生進行思考. 另外,還可在圓的知識背景中講解四點共圓的性質,或是基于幾何旋轉來看待模型中的全等關系. 教學中教師要關注學生的思維活動,及時啟發學生進行思考,充分引導學生構造模型、轉化條件,激發學生的思維,使學生充分掌握模型.
總之,對角互補四邊形模型的應用價值極高,學生在探究過程中需切換視角全面剖析,可從幾何旋轉、三角形全等、四點共圓等角度深入解讀,關注模型的解析思路,理解模型的性質特征,掌握模型的應用策略,形成分析模型的解題習慣.
3266501908251

