超大跨度小凈距隧洞群影響分區與工序研究

隨著交通量增大和公路等級提高，超大斷面的小凈距隧道也不斷出現。文章依托成都天府機場高速公路龍泉山1號隧道工程，建立了平面有限元模型，利用強度折減法計算了雙洞平行小凈距隧道的強度儲備并得到了近接影響分區;其次，利用三維數值計算有限元研究分析了超大斷面四線并行隧道的施工順序，得到了以下結論：（1）圍巖越軟弱，產生的塑性區范圍越大;而當先開挖的隧道埋深增大時，單隧道圍巖穩定性安全系數降低，整體強影響區域的范圍也會變大。那么，埋深更大工況時大跨度小凈距隧道時的安全距離更大。（2）超大跨度小凈距隧道需要控制最小凈距保持中夾巖的穩定，避免后行隧道開挖影響先行隧道的穩定。（3）三車道小凈距隧道影響分區也主要為梯形，三車道小凈距隧道近接影響區變化基本規律與雙車道工況基本一致，由于三車道隧道跨度更大，塑性區更大，所以小凈距隧道的影響范圍較雙車道小凈距隧道的影響范圍更大。（4）龍泉山1號四線小凈距超大斷面隧道應先開挖D3線，再一次開挖D1線、K線與D2線。

超大斷面隧道; 公路; 小凈距; 數值模擬

U452.2+6?? A

[定稿日期]2021-08-02

[作者簡介]王紅喜（1972～），男，本科，高級工程師，主要從事工程單位路基、橋梁、隧道等建設工作。

近年來，公路基礎設施修建標準逐步提高，涌現出諸多超大斷面、小凈距公路隧道，對設計與施工提出了新的挑戰。

國內外學者就小凈距隧道的施工力學行為已經有較為完善地研究。日本在地下工程近接施工領域有較為詳盡地研究，日本《既有鐵路隧道近接施工指南》中根據不同近接類型對既有隧道近接建筑物的施工提出了相應對策[1]。日本盾構隧道施工指南中提出土壓力可以用于判定近接施工的影響程度與影響范圍[2]。在上海越江隧道技術指南[3]的編制中中則充分參考了以上兩個指南。小凈距隧道中凈距的大小與中夾巖的圍巖強度指標是影響其近接分區的重要指標[4-5]。孔超[6]基于強度折減法利用圍巖強度儲備指標得出了隧道平行近接施工影響分區。章慧健與郭蕾[7]研究分析了城市隧道近接既有建筑物的對策。

此外，設計與施工中還要同時考慮超大斷面與小凈距的共同作用。由于塑性區的大小與斷面大小有直接關系，因此，超大斷面隧道小凈距隧道的塑性區也變大，直接影響其修建難度。目前，大斷面公路隧道的修建仍主要依據工程經驗類比的方法。張俊儒等[8]全面調查綜述了中國四車道及以上超大斷面公路隧道當前的修建技術水平，并在此基礎上闡述了超大斷面隧道施工工法與設計理論方面的不足，提出目前深埋圍巖壓力的計算沒有說服力的計算理論。張業民[9]提出“夾巖薄弱面”的概念指導小凈距隧道施工。

根據文獻綜述可知，目前已存在較多近接隧道工程與超大斷面隧道工程，然而針對小凈距超大斷面隧道群的研究卻有限。本文依托成都天府機場高速公路龍泉山1號隧道工程，利用有限元數值計算首先研究了雙洞平行小凈距隧道的強度儲備并得到了近接影響分區;其次，研究了超大斷面四線并行隧道的施工順序。

1 工程概況

1.1 工程背景

成都天府機場高速龍泉山1號隧道位于在天府新區太平鎮穿越龍泉山，至簡陽市五指鄉。設計為4洞隧道，分別為D1、K、D2、D3隧道。隧道斷面布置從左向右依次為2車道+3車道+3車道+2車道，各隧道位置關系如圖1所示。龍泉山1號隧道進口洞口段四洞相鄰兩隧道凈間距（開挖輪廓）分別為：D1線與K線10.5 m，K線與D2線12.75 m，D2線與D3線9.5 m;各洞之間凈間距均小于1倍隧道開挖寬度。

1.2 工程地質

隧址區屬侵蝕剝蝕構造低山地貌，區內溝谷縱橫，山巒起伏，地形切割較強烈，受巖性和構造控制，為典型的背斜成山，龍泉山1號隧道出口為順向坡，坡度與巖層傾角基本一致。隧址區內出露出地層主要有第四系全新統坡殘積層、崩坡積層、沖洪積層、滑坡堆積層，中生界中統遂寧組、中統沙溪廟組粉砂巖、粉砂質泥巖、細砂巖。

場地水文地質條件簡單，第四系松散層孔隙水埋藏淺，分部零星，水量貧乏，基巖孔隙裂隙水，含水層與隔水層相間，層間水力聯系差，局部地下水具承壓性，富水性也不強的特點。

2 小凈距隧道近接影響分區

小凈距隧道的施工通常利用隧道施工的時間與空間效應，先行隧道與后行隧道拉開施工距離。因此，本節利用強度折減法計算隧道的強度儲備時僅計算雙洞平行小凈距隧道工況，并據此研究得到小凈距隧道近接影響分區。強度折減法在有限元中的應用可參考文獻[10-15]，這里不再贅述。

2.1 數值模型

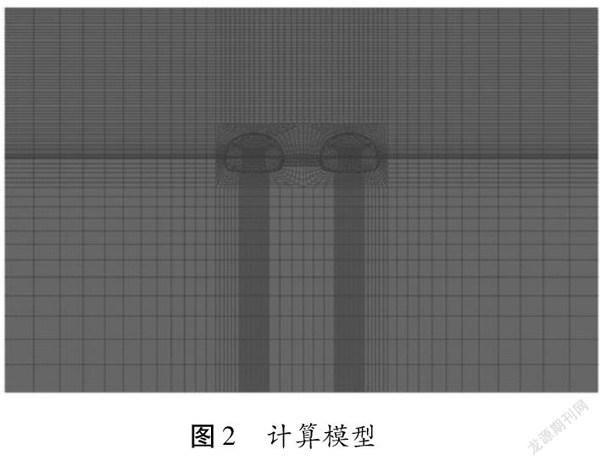
數值模型利用FLAC3D進行建模，利用極限狀態分析法計算隧道開挖后圍巖穩定性安全系數，基于安全系數得到近接影響穩定性分區，數值模型如圖2所示。

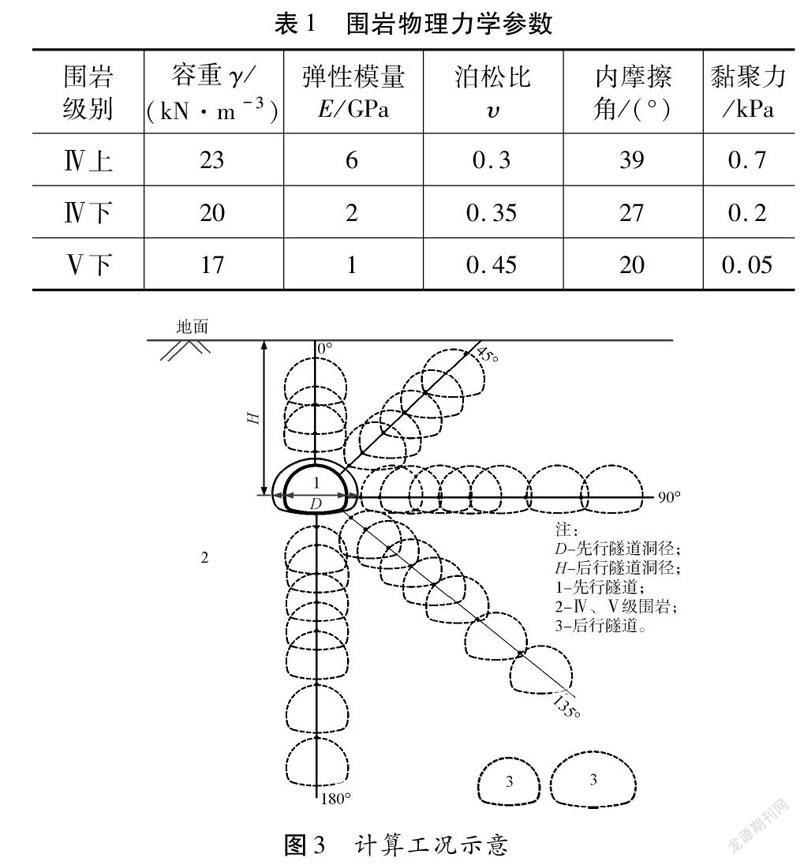
2.2 計算參數與工況

龍泉山1號隧道小凈距段主要為V級圍巖，因此，本節計算中考慮圍巖的上限與下限參數，圍巖物理力學參數同如表1所示。計算工況如表2所示。計算工況示意圖如圖3所示。需要說明的是，龍泉山1號隧道四隧道并非在同一水平線上，存在一定高差，因此這里計算研究影響分區規律時，同時計算了不同角度近接的工況。

2.3 計算結果

首先，需要說明影響分區的標準：

（1）計算單個隧道無支護安全系數F1;

（2）計算后行隧道無支護安全系數F2;

（3）計算兩隧道整體安全系數F3;

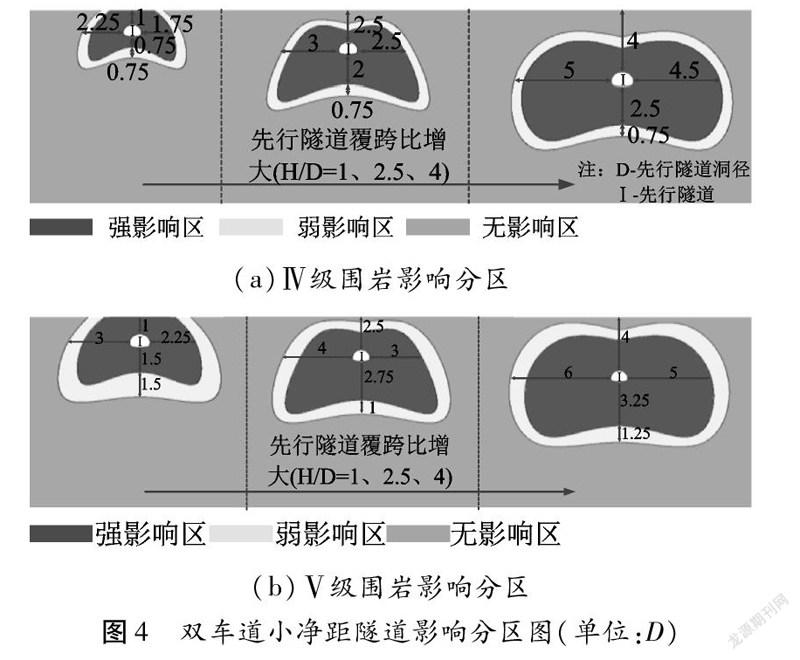
（4）若F3=min（F1，F2），則視為隧道近接無影響;若F3<min（F1，F2），則視為有影響;得到小凈距隧道不同位置時F3=min（F1，F2）坐標點，作出安全系數等值線，如圖4所示。

根據圖4可知，兩雙車道隧道小凈距平行近接時，中夾巖越弱，近接施工影響的區域越大，這是由于圍巖越軟弱，產生的塑性區范圍越大;而當先開挖的隧道埋深增大時，單隧道圍巖穩定性安全系數降低，整體強影響區域的范圍也會變大。那么，埋深更大工況時大跨度小凈距隧道時的安全距離更大。

圖5為三車道小凈距隧道影響分區圖。根據圖5可知，三車道小凈距隧道影響分區也主要為梯形，三車道小凈距隧道近接影響區變化基本規律與雙車道工況基本一致，由于三車道隧道跨度更大，塑性區更大，所以小凈距隧道的影響范圍較雙車道小凈距隧道的影響范圍更大。

3 四線隧道施工順序研究

前文研究基于二維平面計算，雖然二維數值計算能夠在平面應變假定下分析隧道開挖后的強度儲備問題，然而在實際現場施工過程中，小凈距大跨度隧道的穩定性不可忽略施工時空效應的影響。本章擬利用三維數值計算模擬施工過程中夾巖塑性區變化，用于確定適當的施工順序。龍泉山一號隧道小凈距段雙車道隧道埋深為18～28 m，三車道隧道埋深為29～33 m。這里計算兩種工況，分別為工況1先施工兩側雙車道隧道（D3與D1）;工況2先施工中間三車道隧道（D2與K）。

3.1 計算模型

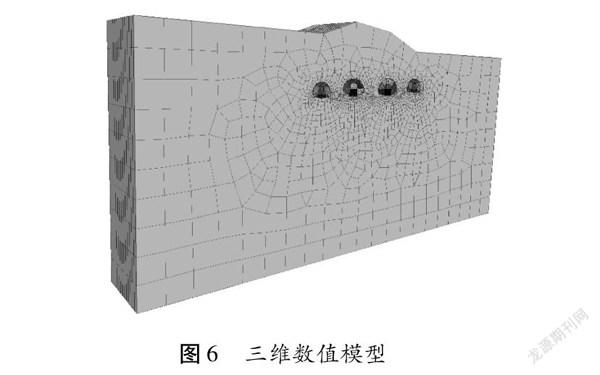
隧道圍巖與初期支護均采用實體單元，二次襯砌采用殼單元。隧道圍巖服從摩爾庫倫本構模型，初期支護與二次襯砌服從彈性本構。該模型共有84 105個單元，51 342個節點。三維數值模型如圖6所示。計算時雙車道隧道采用三臺階七步法，三車道隧道采用雙側壁導坑法。

3.2 計算參數

隧道圍巖參數采用表1中V級圍巖參數，結構支護參數如表3所示。

3.3 計算結果

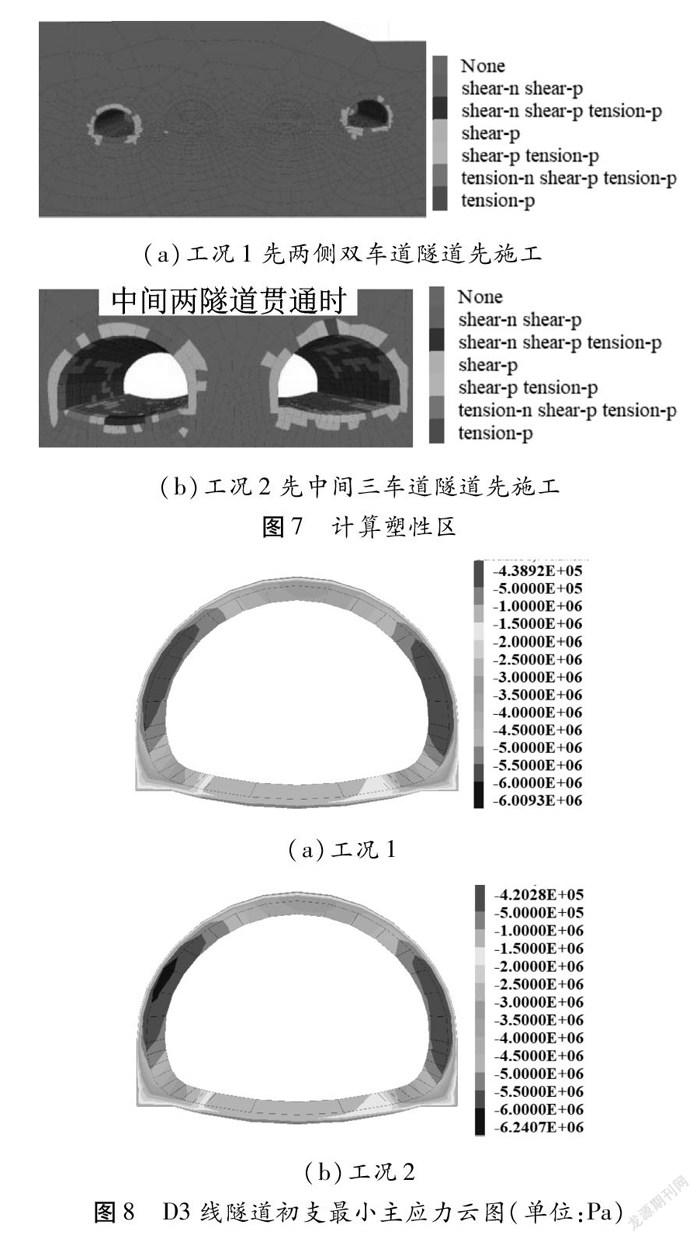
本節計算結果僅呈現夾巖塑性區情況。工況1與工況2的塑性區如圖7所示。D3線隧道初支最小主應力云圖如圖8所示。

根據圖7可知，工況1先開挖兩側的雙車道隧道，兩隧道的凈距較大，遠大于2.5倍洞徑，兩隧道開挖不會相互影響，中夾巖未出現塑性區。工況2先開挖中間的兩個三車道隧道，施工完后再依次開挖兩側的雙車道隧道，后行隧道與先行隧道中夾巖已出現塑性區，需要對中夾巖加固，保證夾巖的穩定。圖8以D3隧道初支為對象，考察其最小主應力，工況2施工過后，D3隧道初支最小主應力絕對值也稍大于工況1。因此，筆者認為選擇工況1的施工工序更為合適，即先開挖D3線，再一次開挖D1線、K線與D2線。

4 結論

本文依托成都天府機場高速公路龍泉山1號隧道工程，建立了平面有限元模型，利用強度折減法計算了雙洞平行小凈距隧道的強度儲備并得到了近接影響分區;其次，利用三維數值計算有限元研究分析了超大斷面四線并行隧道的施工順序，得到了以下結論：

（1）圍巖越軟弱，產生的塑性區范圍越大;而當先開挖的隧道埋深增大時，單隧道圍巖穩定性安全系數降低，整體強影響區域的范圍也會變大。那么，埋深更大工況時大跨度小凈距隧道時的安全距離更大。

（2）超大跨度小凈距隧道需要控制最小凈距保持中夾巖的穩定，避免后行隧道開挖影響先行隧道的穩定。

（3）三車道小凈距隧道影響分區也主要為梯形，三車道小凈距隧道近接影響區變化基本規律與雙車道工況基本一致，由于三車道隧道跨度更大，塑性區更大，所以小凈距隧道的影響范圍較雙車道小凈距隧道的影響范圍更大。

（4）龍泉山1號四線小凈距超大斷面隧道應先開挖D3線，再一次開挖D1線、K線與D2線。

參考文獻

[1] 日本鐵道綜合技術研究所. 接近既有隧道施工對策指南[M]. 日本：鐵道綜合技術研究所情報管理部，1996

[2] 日本土木學會. 隧道標準規范（ 盾構篇） 及解說[M]. 北京： 中國建筑工業出版， 2006.

[3] 越江隧道保護區內新建工程施工對既有越江隧道的影響及控制技術研究技術指南[M]. 2011.

[4] Hoek. Underground excavations in rock[M]. London： Institution of Mining and Metallurgy， 1980.

[5] 聞毓民. 兩孔平行盾構隧道近接施工的力學行為分析[D]. 成都：西南交通大學， 2005.

[6] 孔超. 大規模高密度城市隧道群施工力學行為研究[D]. 成都：西南交通大學， 2016.

[7] 章慧健， 郭蕾， 鄭余朝， 等. 城市隧道近接建筑物施工的影響與對策分析[J]. 鐵道工程學報， 2016（4）：96-100.

[8] 張業民， 李文劍， 李進才. 深埋偏壓小凈距隧道施工力學特征數值模擬研究[J]. 力學與實踐， 2011（2）：46-51.

[9] 鄭穎人， 阿比爾的， 向鈺周. 隧道穩定性分析與設計方法講座之三：隧道設計理念與方法[J]. 隧道建設， 2013，33（8）：619-625.

[10] 鄭穎人， 王永甫. 隧道穩定性分析與設計方法講座之一：隧道圍巖壓力理論進展與破壞機制研究[J]. 隧道建設， 2013，33（6）：423-430.

[11] 鄭穎人， 趙尚毅， 宋雅坤. 有限元強度折減法研究進展[J]. 后勤工程學院學報， 2005（3）：1-6.

[12] 阿比爾的， 鄭穎人， 馮夏庭， 等. 極限應變法在圓形隧洞穩定分析中的應用[J]. 應用數學和力學， 2015，36（12）：1265-1273.

[13] 阿比爾的， 馮夏庭， 鄭穎人， 等. 巖土類材料應變分析與基于極限應變判據的極限分析[J]. 巖石力學與工程學報， 2015，34（8）：1552-1560.

3877500589269