Discontinuous event-trigger scheme for global stabilization of state-dependent switching neural networks with communication delay?
Yingjie Fan(樊英杰), Zhen Wang(王震), Jianwei Xia(夏建偉), and Hao Shen(沈浩)
1College of Electrical Engineering and Automation,Shandong University of Science and Technology,Qingdao 266590,China
2College of Mathematics and Systems Science,Shandong University of Science and Technology,Qingdao 266590,China
3School of Mathematical Science,Liaocheng University,Liaocheng 252059,China
4College of Electrical and Information Engineering,Anhui University of Technology,Ma’anshan 243032,China
Keywords: global stabilization, state-dependent switching neural networks, discontinuous event-trigger scheme,communication delay
1. Introduction
The last decade has displayed an ever-increasing research topic on state-dependent switching neural networks(SDSNNs), such as memristive neural networks, since it has some outstanding superiorities in multi-value storage,[1]and unsupervised learning,[2]etc. Compared with traditional neural networks,some experiment results have demonstrated that SDSNNs can imitate the synaptic activity better in the brain emulation. Accordingly, an enormous interest has been attracted to the investigation of SDSNNs and many pioneering works have been presented,such as synchronization,[3-10]state estimation.[11-14]It is noteworthy that stability is a prerequisite for ensuring SDSNNs steadily operation. As such,various control schemes have been developed to investigate the stabilization problem of SDSNNs.[15-18]Nevertheless,all the above published results are on the basis of an assumption that there are no communication delay and any constraints on the digital transmission channel. From a resource conservation of view,these traditional control schemes in Refs.[3-19]will lead to transmission burdens and increase control cost.With the increasing demand of digital technology in industry,a rich synthesis of energy-saving networked control schemes,such as impulsive control,[20-22]sampled-data control,[23-26]and event-triggered control,[27-40]compose a popular research issue in relevant applications domains. Clearly,it is necessary and reasonable to settle the stabilization problem of SDSNNs under networked control schemes.
As we know, the sampling information is sent out at a series of transmission instants. It can be found that the time-dependent mechanism is easy to realize by using a clock generator. However, the redundant sampling information is still transmitted to the controller if some desirable targets are satisfied. Hence, it will lead to a waste of energy resources and communication bandwidth. To this end, several event-trigger schemes have been established to reduce the unnecessary sampling times, such as continuous event-trigger(CET),[27-29]sampled-data-based event-trigger,[30-36]and discontinuous event-trigger(DET).[37-41]For example,the global synchronization problem of SDSNNs with parameters mismatch has been investigated via continuous event-triggered control in Ref.[29]. Also,theoretical analysis has proved that the Zeno behavior can be avoided. However, the derived results in Ref.[42]demonstrate that the Zeno behavior may be still exist under the influence of arbitrary small measurement noise or external disturbances. To overcome this shortcoming,the global stabilization of SDSNNs has been discussed under sampled-data-based event-triggered control in Ref. [34].Unfortunately, this kind of trigger scheme does not take advantage of the available state information. In view of the above considerations,the DET scheme consisting of two work modes has been proposed in Ref.[37]for the first time,which can not only avoid Zeno behavior but also reduce the triggering times. For instance, the global stabilization of SDSNNs has been achieved based on an exponential-attenuation-based DET scheme and the simulation results have demonstrated that the triggering times can be effectively reduced in Ref.[38]. It is, therefore, meaningful to investigate the stabilization problem of SDSNNs by using DET scheme.
On the other hand, an ineluctable issue is that the sampling information transmitted from the controller to actuator is usually influenced by network-induced communication delay.[43,44]Under the effect of communication delay, it is difficult to achieve a satisfactory performance. Accordingly,how to ensure the stability of networked control systems with communication delay is an important and necessary problem. To this end, the global stabilization problem of networked T-S fuzzy control systems has been investigated under adaptive event-triggered control with communication delay in Ref.[35]. In addition,a class of event-trigger predictive control scheme, to compensate communication delays, has been proposed for networked control systems(NCSs)in Ref.[36].Nevertheless,there are no published results to study the analysis and synthesis of SDSNNs under discontinuous eventtriggered control under the framework of communication delay. The main reason lies in that the proposed analysis techniques in Refs. [38,40,41] cannot be applied to deal with the stability of SDSNNs under discontinuous event-triggered control subject to communication delay.This naturally touches off the following important problems. What is the impact of communication delay on data transmission? Furthermore, what is the effect of communication delay on the trigger times and stability performance? To the best of our knowledge, these difficulties have not been solved for SDSNNs with communication delay by employing DET scheme. Therefore, how to well settle these problems motivates the present investigation of this paper.
Summarizing the above discussions, this paper investigates the global stabilization of SDSNNs under discontinuous event-triggered control with communication delay. The main contributions are listed as follows.
(i)Considering the effect of communication delay,a fictitious delay function is proposed by utilizing the convex combination technique. Then, the SDSNNs and trigger condition are respectively transformed into two tractable models,which contributes to the current theoretical analysis.
(ii) A unified framework is proposed that has the ability to deal with the simultaneous existence of the properties of discontinuous event-trigger scheme,communication delay,as well as feedback controller design. First, a novel Lyapunov-Krasovskii functional is constructed to investigate the stability of the resulting closed-loop SDSNNs. Then, by employing the extended reciprocally convex combination method and some inequality estimation techniques,two novel globally asymptotically stability criteria are respectively established for the resulting closed-loop SDSNNs under discontinuous eventtriggered control with communication delay.
Notations:Throughout this paper, N, Rn×ndenote the set of nonnegative integers, n×n real matrices, respectively.diag(···)and A(i)respectively denote a block diagonal matrix and the i-th row of matrix A. AT(A?1) stands for transpose(inverse) of matrix A. A >0 (A ≥0) means that A is a symmetric and positive definite (semi-definite) matrix. col{···}is a column vector. λmax(A) denotes the maximal eigenvalue of matrix A. ||·||p, p=1,2,∞and I (0) are the p-norm of a vector or a matrix and identity (zero) matrices of appropriate dimensions.
2. Preliminaries and problem formulation
Consider the following dynamical system for n-neurons SDSNNs:
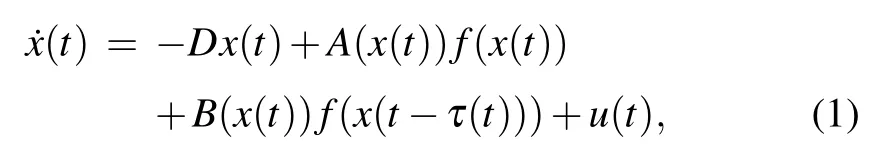
where x(t)∈Rnand u(t)∈Rndenote the state vector and controller, respectively. D=diag{d1,d2,...,dn}>0, A(x(t))=(aij(xj(t)))n×n,and B(x(t))=(bij(xj(t)))n×nrespectively denote the self-feedback matrix,state-dependent switching connection weight matrix,and delayed connection weight matrix.τ(t)denotes the time-varying delay satisfying 0 ≤τ(t)≤τ and ˙τ(t)≤μ <1. The neuron activation function f(x(t))∈Rnis assumed to be monotonically nondecreasing and satisfies 0 ≤fj(u)?fj(ν)/(u?ν)≤Lj, u, ν, u/=ν, Lj∈R, i,j =1,2,...,n. The state-dependent switching connection weights satisfy the following conditions:
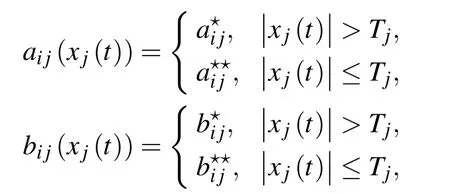
Also,one can see that equation(1)is the characteristic of differential dynamical systems with discontinuous right-hand sides. In this case, we consider the trivial solutions of system (1) in Filippov’s sense and the following Definition 1 is introduced.
Definition 1[45]Consider the system ˙y(t)=g(y),y ∈Rnwith discontinuous right-hand sides, a set-valued map is described as

where B(y,δ)={z:‖z ?y‖≤δ},co[E]is the closure of the convex hull of set E, and μ(N) is the Lebesgue measure of set N. A solution in Filippov’s sense of the Cauchy problem,for the system with initial value y(0)=y0, is an absolutely continuous function y(t),t ∈[0,T]. It satisfies y(0)=y0and differential inclusion
˙y(t)∈φ(y)
for a.e.t ∈[0,T].
Define

Based on Definition 1,system(1)is equivalent to
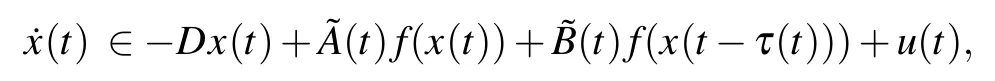
where

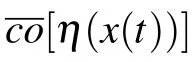
such that


In this paper, we consider the stabilization problem of SDSNNs via discontinuous event-triggered control. As displayed in Fig.1,a discontinuous event-trigger(DET)scheme is positioned between the controller and the sensor. The corresponding trigger condition is formulated as

where the waiting time h >0, λ ≥0, and trigger matrix Θ ≥0. It should be mentioned that the main feature of this DET scheme lies in that the operation pattern consists of rest interval and work interval. The principle is as follows. Suppose that the k-th event is activated on the basis of trigger condition (3). Then, the sampling information x(sk)is transmitted from the event generator to the controller.Meanwhile, the trigger scheme rests for h seconds. At time sk+h, the DET scheme begins to work. Once the trigger condition (3) is violated, the next (k+1)-th event satisfying (x(t)?x(sk+1))TΘ(x(t)?x(sk+1))>λxT(t)Θx(t) is activated. Repeating the above reasoning, it is easy to see that the Zeno phenomenon can be avoided by using DET scheme since the inner-event interval is not less than h seconds.

Fig.1. Schematic diagram of an event-triggered control SDSNNs.
The control law in system(2)is designed as
u(t)=Kx(sk),
where K is the control gain matrix to be determined.
Taking the network-induced delay into account,denote by δk∈[0,δM]over all communication delay from the controller to the actuator. From Fig.1,one can see that the communication delay δkaffects the transmission of sampling information x(sk). Here, we set tk=sk+δkas the ZOH updating time,which is satisfied
tk=sk+δk≤sk+1+δk+1=tk+1.
Then,the closed-loop system(2),for[tk,tk+1),has the resulting form

Remark 1According to the characteristics of DET scheme,we would like to transform the closed-loop SDSNNs(4) into a system which switches between the rest interval t ∈[tk,tk+h)and work interval t ∈[tk+h,tk+1).However,owing to the effect of the communication delay δk,such a switching case will not happen if tk+h=sk+δk+h ≥sk+1+δk+1=tk+1. Accordingly, the trigger condition (3) and closed-loop system(4)should be reconsidered.
In view of the foregoing discussions, rewrite system (4)as follows:
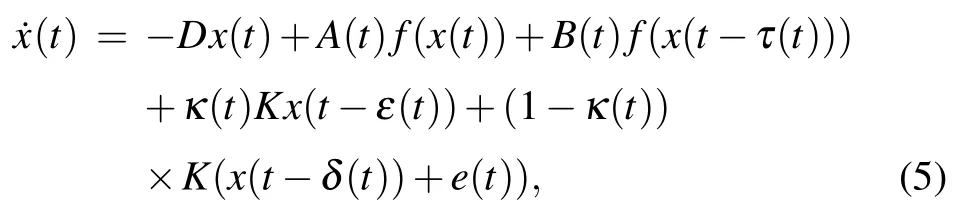
where
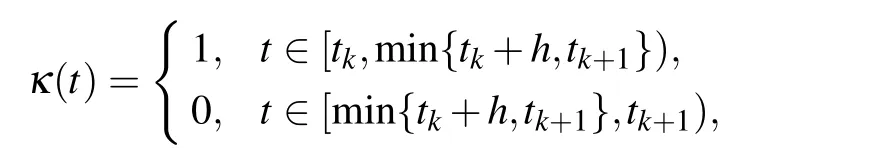
ε(t)=t ?sk≤h+δM=εM, t ∈[tk,min{tk+h,tk+1}),
e(t)=x(sk)?x(t ?δ(t)), t ∈[min{tk+h,tk+1},tk+1).

Fig.2. The illustration of the sampling and transmission sequence whentk+h <tk+1.
Here, δ(t) ∈[0,δM] is a fictitious delay function. As shown in Fig.2,owing to t ?δ(t)∈[sk+h,sk+1),δ(t)can be presented as a simple convex combination with δ(tk+1)=δk+1and δ(tk+h)=δk,i.e.,

Therefore,the trigger condition(3)can be written as

Before deriving the main results,the following lemma is introduced.




4. Related work
Considering the effect of communication delay,the main difficulties and contributions will be discussed in this section.
(i)Proof of Theorem 1
It should be mentioned that,for ε(t)∈[0,δM]and κ(t)=1, the closed-loop system (5) can be described by itself with κ(t)=0 and e(t)=0. Clearly,the trigger scheme(6)can be guaranteed. In this case, the condition (7) in Theorem 1 ensures ˙V(t)≤0 for system (5) with ε(t)∈[0,δM], κ(t)=1.As such,we,here,just consider the dynamic behavior of system(5)with ε(t)∈(δM,εM]and κ(t)=1.
(ii)Robustness to communication delay
In this paper, the main difficulty is how to analyze the stability of the trivial solutions of closed-loop system(5)under discontinuous event-triggered control subject to network-induced communication delay. Unlike the previous works,[38,40]the closed-loop systems switching between the rest interval and work interval may not occur if sk+δk+h ≥sk+1+δk+1. Accordingly, the developed system models and analysis approaches in Refs. [38,40] cannot be applied in this paper. To overcome these difficulties, a fictitious delay function δ(t) is designed by utilizing the convex combination method. Then, a novel closed-loop system (5) and the related trigger condition (6) are respectively established with the aid of δ(t). In addition, the other challenge is how to investigate the stability of system (5). To this end, the proof of Theorem 1 is divided into two steps, i.e., κ(t)=1,δ(t)∈[0,δM] and κ(t)=0, ε(t)∈(δM,εM]. Meanwhile, by using the constructed Lyapunov-Krasovskii functional and extended reciprocally convex inequality technique, a new globally asymptotically stability criterion is derived for closedloop SDSNNs(5)with communication delay under discontinuous event-triggered control. As such,a unified framework,to reflect the engineering practice, is proposed that aims to handle the problem of simultaneous existence of the communication delay,discontinuous event-triggered control,and feedback controller design. It can not only make full use of the advantage of the DET but also guarantee enough resilience requirement and satisfactory performance influenced by communication delay and limited network resources.
5. Numerical simulation
Example 1Taken from Refs.[50], a chaotic SDSNN is proposed and the related system parameters are described by

and f(x(t))=tanh(x(t)), τ(t)= et/(1+et), D=diag(1,1).Thus,we can obtain L=diag(1,1),τ =1,μ =0.25,


Using the above parameters, figure 3 demonstrates that the global stabilization of the closed-loop SDSNNs (5) with communication delay can be achieved under discontinuous event-triggered control. In the following, the influence of the waiting time h and communication delay δMon the number of triggering times are respectively discussed.
Case 1 To depict the effect of h on the triggering times,choose ξ =1, λ =0.01, δM=0.01, and some calculations are shown in Figs.4 and 5. Figure 4 displays the release times with the different values of waiting time h over[0 s,5 s].From Fig.5,we can conclude that the triggering times will decrease when h increases. That is to say,the average period arwill become large. Accordingly,it is clear that the limited bandwidth and computational resources can be effectively saved with the increasing of h.
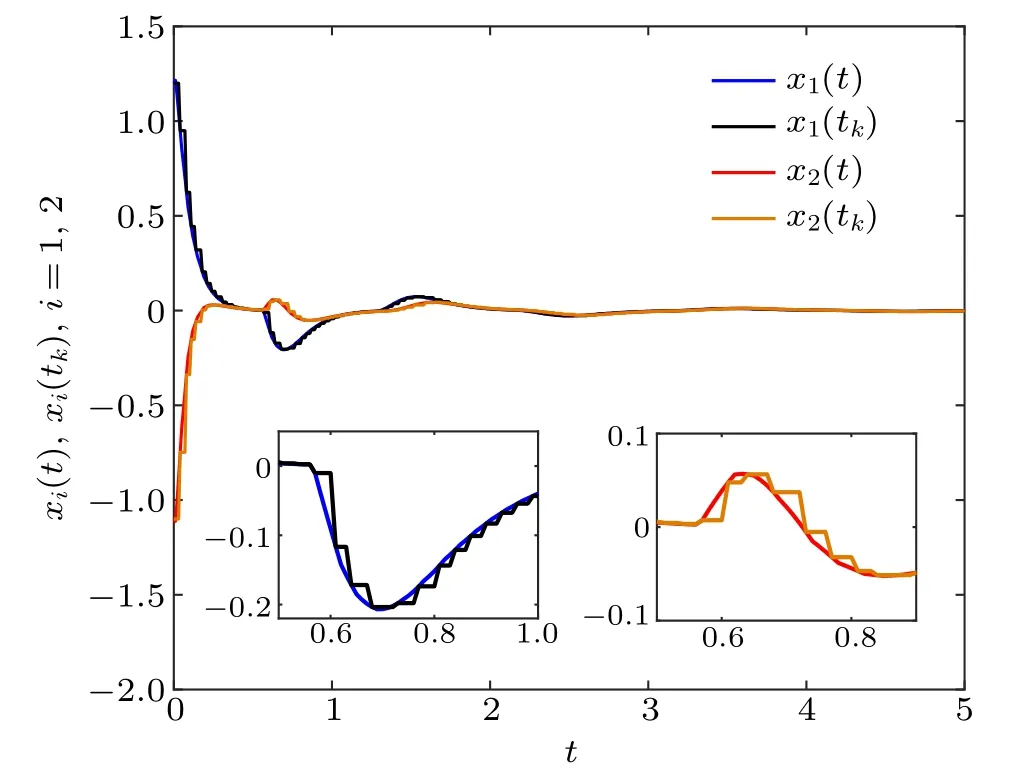
Fig.3. Evolutions of xi(t),xi(tk),i=1,2 under DET scheme(6).
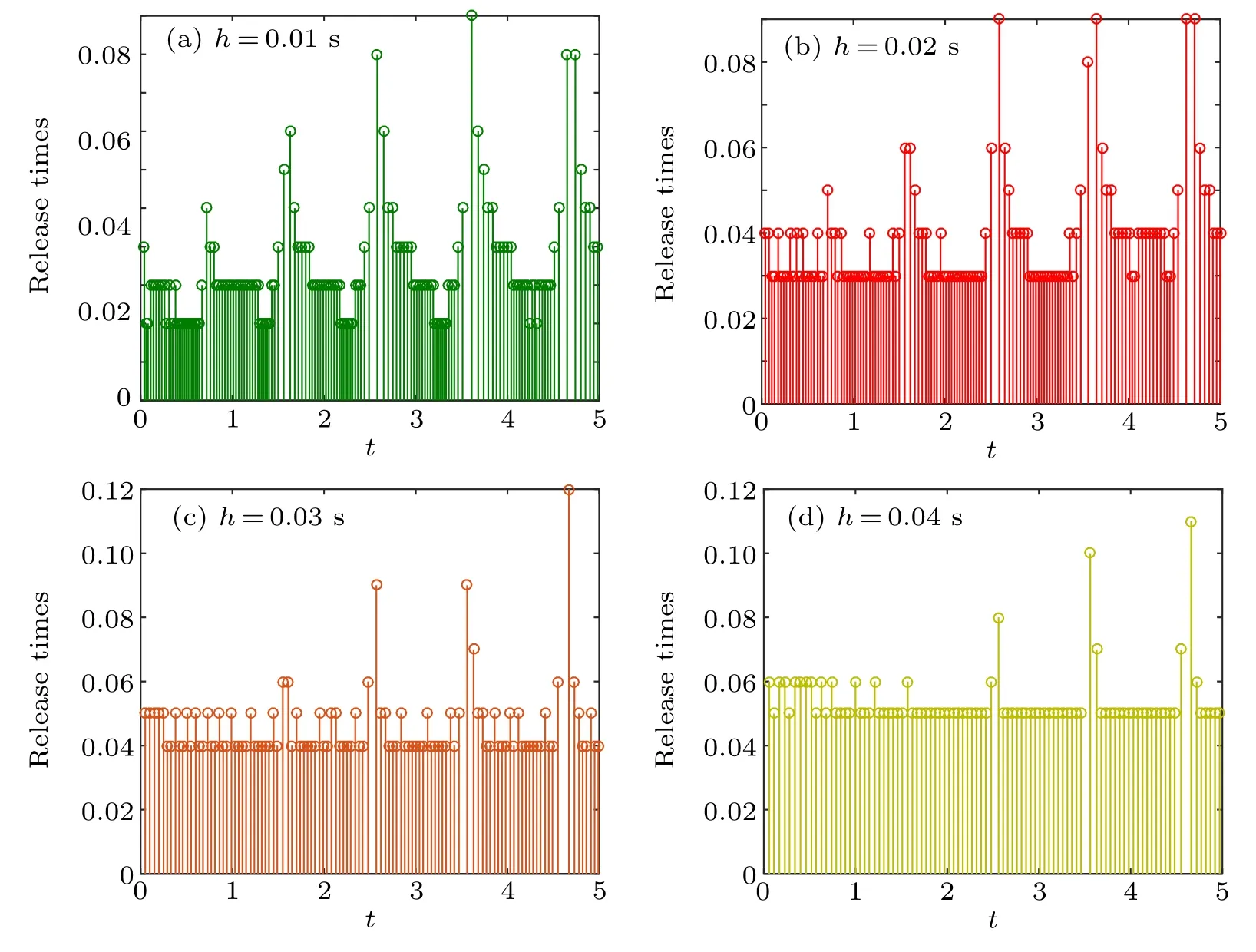
Fig.4. Event release instants with different h for ξ =1,λ =0.01,δM =0.01.

Fig.5. Triggering times tr for different waiting time h.

Fig.6. Triggering times tr for different communication delay δM.
Case 2For fixed ξ =1, λ =0.01, h=0.01, set δM=0.005l,l=1,2,3,4,5,6,figure 6 and Table 1 display the evolution of triggering times tr. From Fig.6 and Table 1, it can be seen that only 135 data signals are transmitted when δM= 0.005. However, it is noteworthy that the amount of triggering times will increase if the communication delay δMbecomes large, which means that the output fluctuation of closed-loop system is large. Namely,the increasing of δMcan aggravate the computational cost and transmission burden of networked control systems.
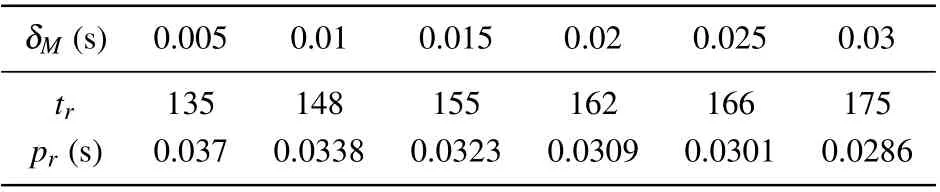
Table 1. For fixed ξ =1, λ =0.01, h=0.01, the triggering times tr,average period pr with different communication delay δM over[0 s,5 s].
From above analyses,it is clear that a larger waiting time h and a smaller communication delay δMcontribute to a better performance of triggering times.
Example 2Consider a 2-neurons SDSNN(1)with τ(t)=et/(1+et), f(x(t))=tanh(x(t)),D=diag(1,1),and

then,one has L=diag(1,1),τ =1,μ =0.25,
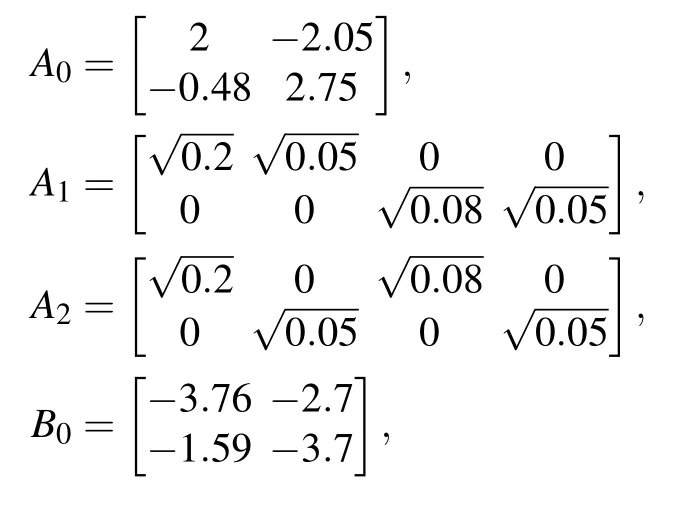

Take h=0.04, ξ =1, λ =0.01, δM=0.01, εM=h+δM=0.05,x(s)=(?0.8,1.3)T,s ∈[?1,0]. As well,combining with Theorem 2, one can obtain the trigger matrix Θ and feedback gain K:
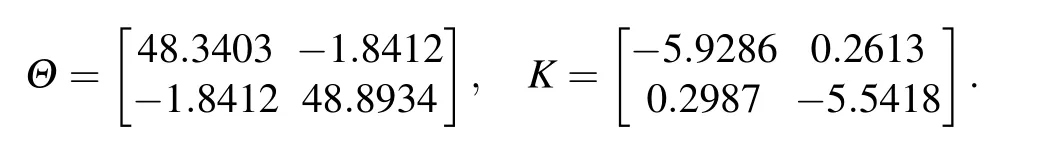
As shown in Fig.7(a), it can be seen that the state responses xi(t) and xi(tk) (i=1,2) of system (6) converge to origin. Furthermore,figure 7(b)displays the event release instants over[0 s,12 s].One can obtain the trigger times tr=187 and average period ar=0.0642 s. It implies that the global stabilization of system (6) can be achieved via discontinuous event-triggered control with communication delay.

Fig.7. (a)Evolutions of xi(t),xi(tk),i=1,2;(b)event release instants over[0 s,12 s]under DET scheme(6).
It should be mentioned that when λ = 0 and h = 0 in system (6), the DET control will degenerate into periodic sampled-data (PS) control and CET control, respectively. In order to display the advantage of DET, some comparisons are illustrated as follows. Set the initial value as x(s) =(?0.8,1.3)T,s ∈[?1,0],h=0.01,ξ=1,λ=0.1,and δM=0.In terms of Theorem 2,the triggering times for different control schemes are displayed in Table 2. Compared with the PS and CET,it is easy to see that the number of triggering times,based on DET(3),is respectively reduced more than 91%and 86%. It means that the limited network resources can be effectively saved by using DET control.
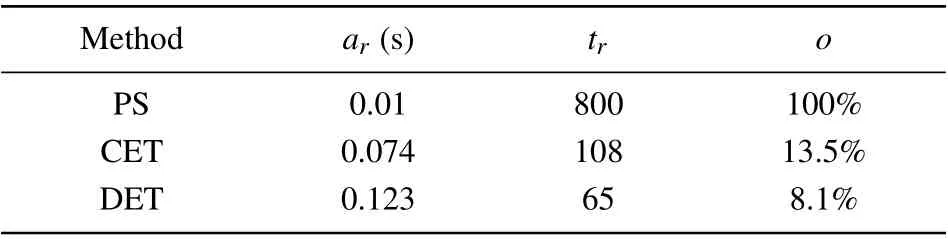
Table 2. Comparisons of the average release period ar,triggering times tr,and data transmission rates o for h=0.01,ξ=1,λ=0.1,and δM=0 over[0 s,8 s].
6. Conclusion
The global stabilization problem of SDSNNs is developed under discontinuous event-triggered control with communication delay. Considering the influence of communication delay, the trigger condition and SDSNNs are transformed into two tractable models by introducing a fictitious delay function.Then, a Lyapunov-Krasovskii functional is designed for the resulting closed-loop SDSNNs. Meanwhile, some inequality estimation techniques and extended reciprocally convex combination method are employed to guarantee the stability of the closed-loop SDSNNs. A unified framework is established that is capable of handling the simultaneous existence of the properties of discontinuous event-trigger scheme, feedback controller design, as well as communication delay. Lastly, two examples are given to illustrate the validity of the obtained results. In our future work,the networked privacy problems will be considered in the presence of DET control.In addition,how to extend the developed framework to consider the privacy issues with DET control will be another interesting topic.
- Chinese Physics B的其它文章
- Nonlocal advantage of quantum coherence in a dephasing channel with memory?
- New DDSCR structure with high holding voltage for robust ESD applications?
- Nonlinear photoncurrent in transition metal dichalcogenide with warping term under illuminating of light?
- Modeling and analysis of car-following behavior considering backward-looking effect?
- DFT study of solvation of Li+/Na+in fluoroethylene carbonate/vinylene carbonate/ethylene sulfite solvents for lithium/sodium-based battery?
- Multi-layer structures including zigzag sculptured thin films for corrosion protection of AISI 304 stainless steel?

