城市軌道車輛車體被動式吸振器減振設計研究

宗志祥

（上海地鐵維護保障有限公司 車輛分公司，上海 200235）

隨著民眾生活水平的提高，城市軌道車輛的乘坐舒適度問題越來越受關注。被動式吸振器由于結構簡單，減振性能好等優點[1]，已成為抑制車體振動、提高乘坐舒適度的有效手段之一。

為了降低軌道車輛車體的振動，國內外很多學者將動力吸振器引入到車體上。Tomioka等[2]在將彈性圓環作為動力吸振器安裝在車體下方，能夠有效地降低車輛的彎曲振動；曾京等[3]在車體底架中央布置被動式動力吸振器，認為吸振器在一定程度上能夠抑制車體某些振動頻率成分，但未提出吸振器的具體設計方法。周勁松等[4-7]利用基于二自由度設計的被動式吸振器抑制了彈性車體的振動，引入了車輛運行平穩性指標對車體動力吸振器的減振效果進行評價。文永蓬等[8]考慮車軌耦合作用對被動式吸振器設計參數的影響，對被動式吸振器進行優化設計，但并未提出通用的適用于城市軌道車輛車體被動式吸振器設計方法。綜上，被動式吸振器已經開始應用于軌道車輛車體的減振，但以往的研究都是基于傳統二自由度的吸振器的設計，而車軌耦合振動模型是多自由度復雜系統，傳統被動式吸振器直接嫁接到軌道車輛上，會存在一定的偏差，具有一定的局限性。為此，提出了適用于軌道車輛車體被動式吸振器減振設計方法。

1 含被動式吸振器的車軌耦合振動模型

1.1 系統模型建立與求解

含被動式吸振器的車軌耦合振動模型如圖1所示。視車輛的車體、轉向架、輪對和被動式吸振器為剛體，車身浮沉和點頭運動有兩個自由度，每一個構架浮沉和點頭運動有兩個自由度，每一輪對的垂向運動有四個自由度，被動式吸振器的浮沉運動有一個自由度，分別對應圖中的Zc、φc、Zt1、φt1、Zt2、φt2、Zw1、Zw2、Zw3、Zw4、Zd。軌道系統中，為了簡化計算，選用長枕埋入式無砟軌道[9]，鋼軌的位移采用Zr表示，其余參數如表1所示。

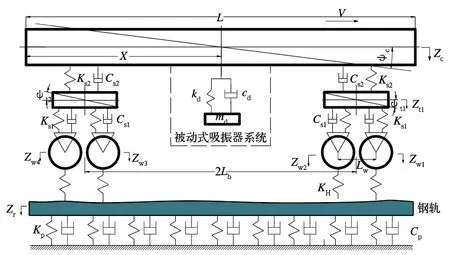
圖1 含被動式吸振器的車軌垂向振動模型

鑒于篇幅限制，只列出車體、被動式吸振器和鋼軌的振動方程分別為：

式中：kd為被動式吸振器的剛度；cd為被動式吸振器的阻尼；L為車體的長度；x為被動式吸振器的安裝位置。由文獻[10]可知，吸振器對車體的中部剛性振動影響較小。為方便計算，被動式吸振器安裝在車體的中部，即x=L/2。

表1 某城市軌道車輛車軌耦合動力學模型的參數

式中：md是被動式吸振器的質量。

式中：Nr為扣件節點總數；M為鋼軌的模態階數；xi為第i個扣件節點的坐標值；Fwj為第j軸輪軌動作用力；xwj為第j軸輪對的坐標值；Yrn(x)、Yrh(x)為鋼軌的振型函數；qrn(t)、qrh(t)為廣義坐標。

根據輪軌耦合關系，將車輛系統和軌道系統進行耦合形成動力學矩陣，并進行傅里葉變換為：

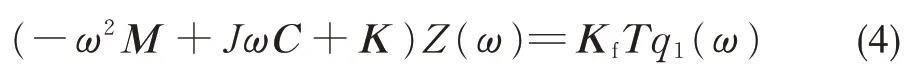
式中：M為系統的質量矩陣；C為受被動式吸振器影響的阻尼矩陣；K受被動式吸振器影響的剛度矩陣；Z(ω)為位移矩陣的傅里葉變換。Kf為系統轉換矩陣；T為時滯矩陣；q1(ω)為系統激勵輸入向量。

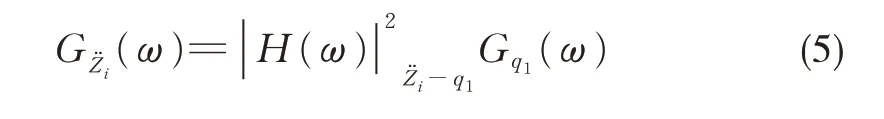
其中

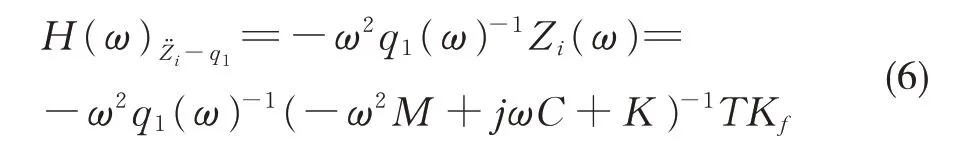
1.2 被動式吸振器參數求解

根據吸振器的減振原理，利用最優同調條件和阻尼條件[11]，對被動式吸振器進行設計。

最優同調條件和阻尼條件分別為：

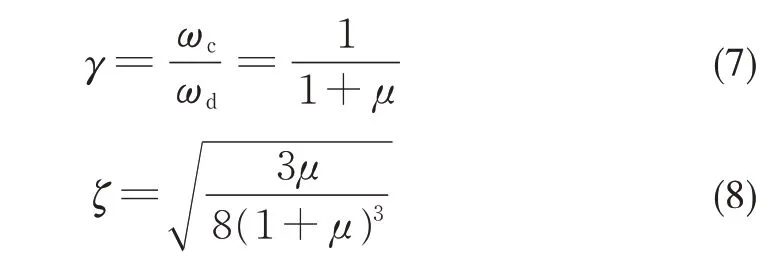
式中：γ、μ、ζ分別為被動式吸振器和車體振動的固有頻率比、質量比和阻尼比；ωc為車體振動固有圓頻率；ωd為被動式吸振器固有圓頻率。

可求得被動式吸振器的剛度和阻尼：

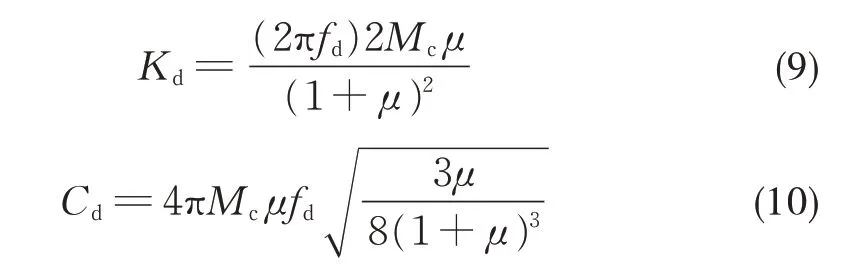
式中：fd為被動式吸振器的目標頻率。

2 傳統被動式吸振器的局限性

傳統的被動式吸振器是基于二自由度設計的，下面分析將傳統被動式吸振器運用在城市軌道車輛上的局限性。

為了更直觀的反映被動式吸振器的減振效果，引入動力放大系數ε：

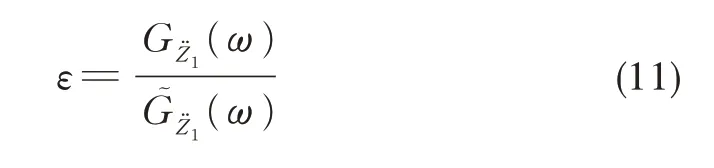
設定車輛在空載工況下，隨機選取車速分別為30 km/h、50 km/h、80 km/h，對應的車體振動頻率分別為1.1 Hz、1.08 Hz、1.23 Hz，此時，針對這3個頻率進行傳統被動式吸振器的設計，其吸振器的目標頻率為1.1 Hz、1.08 Hz、1.23 Hz，如圖2所示。

由圖2可知，3種利用傳統基于二自由度設計的吸振器都有一定的減振效果。這意味著被動式吸振器運用在軌道車輛上具有一定的可行性。此外，3種動力吸振器的動力放大系數最小值分別出現在1.17 Hz、1.16 Hz、1.17 Hz處，偏離了與之對應的車體的固有振動頻率，分別為1.1 Hz、1.08 Hz、1.23 Hz，這說明傳統被動式吸振器雖然有減振效果，但其最佳減振效果偏離了減振最佳頻率點(即與車體振動固有頻率點相互吻合的點，以下簡稱減振最佳點)，這也間接意味著傳統被動式吸振器根據車體振動頻率設計的目標頻率存在一定的偏差。

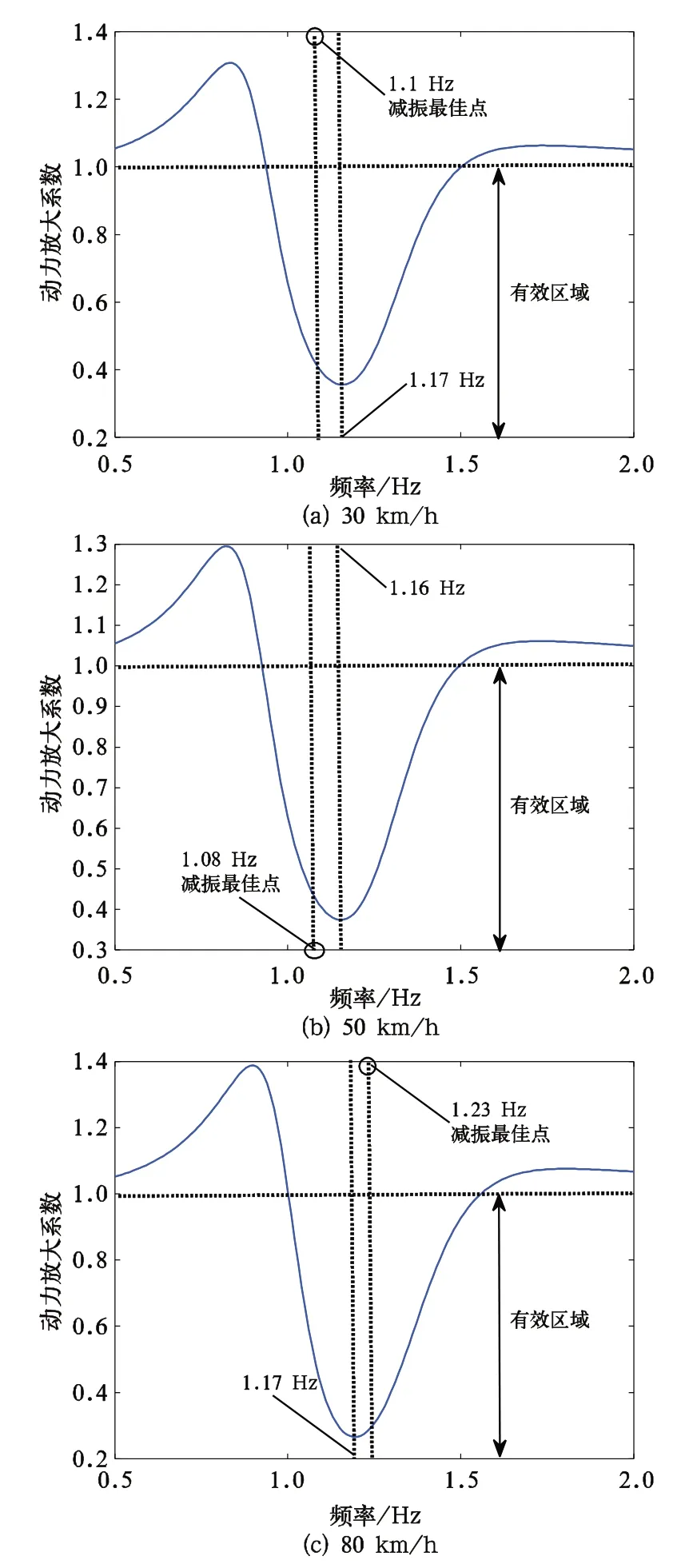
圖2 不同速度下傳統動力吸振器的減振效果

綜上，傳統被動式吸振器運用在城市軌道車輛上，存在一定的局限性，為了改善被動式的減振性能，下面對被動式吸振器的目標頻率做進一步的修正設計。

3 車體被動式吸振器優化設計

為了獲得被動式吸振器的最優目標頻率，考慮到車體的振動在1 Hz附近，令0.5～2 Hz作為遍歷區間，令Gd(ω)為附加被動式吸振器的車體加速度譜，fc為車體的振動頻率，fd為被動式吸振器的目標頻率，fopt為被動式吸振器的最優目標頻率。

可獲得被動式吸振器最優目標頻率fopt的算法如下：

第一步；選定遍歷頻率區間為0.5～2 Hz，頻率間隔為0.01。

第二步：遍歷0.5～2 Hz，獲得每個目標頻率fd下Gd(fc)的最小值，此時所對應的目標頻率fd即為最優目標頻率fopt。

設定車輛在空載狀態下，其運行速度為構造速度80 km/h，獲得不同總質量比下，0.5～2 Hz區間內，車體振動在最優減振頻率點處的加速度譜，如圖3所示。

由圖3可知，減振最佳點處車體加速度譜存在一個最小值，此時對應的目標頻率稱為最優目標頻率，不同質量比對應不同的最優目標頻率。此外，隨著質量比的增加，被動式吸振的減振效果變好，但是大的質量比會使被動式吸振器的體積增大，考慮到車下空間被大量設備占據，剩余空間有限，因此，綜合考慮到車下布置難易程度和經濟性，確定質量比為0.1，此時，對應的吸振器最優目標頻率為1.36 Hz。

圖3 0.5～2 Hz區間內減振最佳點處的車體加速度譜

圖4為被動式吸振器目標頻率1.36 Hz，質量比為0.1的設計下，修正前后被動式吸振器對車體的減振效果圖。

由圖4(a)可知，在減振最佳點處，修正設計前的車體加速度譜為0.003 1，大于修正設計后的車體加速度譜0.002 4，這說明修正設計前的減振效果要低于修正后的減振效果。由圖4(b)可知，修正設計后的動力放大系數在1.23 Hz處出現了最小值，這意味著此時在1.23 Hz處達到了最好的減振效果，與減振最佳點相吻合，未出現偏差。

圖4 修正前后被動式吸振器的減振效果圖

綜上，城市軌道車輛車體被動式吸振器的一般步驟如圖5所示：

第1步，根據車輛的速度、載客量和車軌耦合模型的參數，獲得吸振器目標頻率區間；

第2步，遍歷吸振器目標頻率區間，確定被動式吸振器的最優目標頻率和質量比；

第3步，利用吸振器的最優同調條件和最優阻尼條件獲得被動式吸振器的剛度和阻尼。

4 減振效果驗證

4.1 載客量對減振效果的影響

令車輛運行速度為80 km/h、載客量由空載（AW0）逐漸變為超載（AW3），獲得車體無被動式吸振器和附加被動式吸振器的Sperling平穩性指標對比圖，如圖6所示。

圖5 被動式吸振器減振設計流程圖

圖6 載客量對被動式吸振器減振效果的影響

由圖6可知，隨著載客量的增大，兩種狀態下的車體振動逐漸減小。在整個載客量的區間內，附加被動式吸振器的振動都要小于無被動式吸振器車體的振動，這意味著被動式吸振器發揮出了較好的減振效果，此外，被動式的減振效果由最初的10.9%降為了5.2%，這說明被動式吸振器的減振效果隨載客量變大而減小，這是因為載客量的增加，車體的質量增大導致車下設備的質量比減小，較小的質量比也能降低車體的振動。

4.2 速度對減振效果的影響

圖7為車輛在載客量空載（AW0）下，不同車輛速度下，車體無被動式吸振器和附加被動式吸振器的Sper?ling平穩性指標對比圖。

由圖7可知，隨著速度的增大，車輛的垂向振動并不是呈單調增加的趨勢，而是在共振速度處出現局部峰值[12]。在整個速度范圍下，可以分為3個速度區間，在3個區間范圍內，附加被動式吸振器都取得了較好的減振效果，而在區間接點25 km/h、47 km/h處，減振效果較差。綜合整個車輛運行區間，被動式吸振器獲得了較好的減振效果。

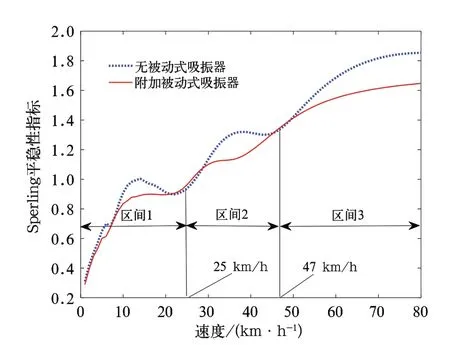
圖7 速度對被動式吸振器減振效果的影響

5 被動式吸振器安裝可行性

城市軌道車輛車下設備眾多，剩余空間有限，因此，需要對被動式吸振器的尺寸作初步估算，以便于工程的實際應用。

被動式吸振器的材料采用性價比較高、密度大的鑄鋼[13]，密度為ρ鋼=7.85 t/m3，根據密度ρ鋼、車體質量Mc和被動式吸振器的質量比μ，可獲得被動式吸振器體積V為：

利用式(12)獲得被動式吸振器的體積為0.432 m3。城市軌道車輛車體寬度3 m，從軌頂面至地板面高度為1 130 mm，被動式吸振器可以安裝在低壓箱的旁邊。考慮到車輛各限界的因素，初步可以估算被動式吸振器的尺寸為：長2 000 mm左右，寬500 mm左右，高500 mm。其安裝示意圖如圖8所示。

圖8 被動式吸振器的安裝示意圖

6 結論

（1）傳統二自由度設計的被動式吸振器直接應用在城市軌道車輛車體上，最佳減振點存在一定的偏差，具有一定的局限性；優化設計后的被動式吸振器的最佳減振點和車體固有頻率點相互吻合，具有最優減振效果。

（2）根據軌道車輛車體振動特性，提出了適用于城市軌道車輛車體被動式吸振器減振設計方法。具體步驟為首先根據車輛的速度、載客量和車軌耦合模型的參數，獲得吸振器目標頻率區間，然后遍歷吸振器目標頻率區間，確定被動式吸振器的最優目標頻率和質量比，最后利用吸振器的最優條件和最優阻尼條件獲得被動式吸振器的剛度和阻尼。

（3）在不同速度和載客量工況下，優化設計的被動式吸振器都取得了較好的減振效果，為利用被動式吸振器來降低車體振動的研究和應用提供了參考依據。