地基不均勻沉降下大型儲罐變形規律和預測方法研究*

陳嚴飛 馬尚 董紹華 婁方宇 孫文勇 趙永濤 孫秉才 倪恒

1中國石油大學（北京）油氣管道輸送安全國家工程實驗室·石油工程教育部重點實驗室·城市油氣輸配技術北京市重點實驗室2大連理工大學工業裝備結構分析國家重點實驗室3中國石油集團安全環保技術研究院

隨著大型國家原油儲備庫不斷興建，原油儲罐日趨大型化。大型儲罐是一種典型的薄殼結構，在石油工業中被廣泛應用于原油及成品油的儲存，具有節約建設成本、減少占地面積、便于管理等優點。大部分儲罐建在地基條件較差的沿海地區，隨著服役年數的增加，儲罐地基常會發生不同程度的沉降。過量的地基沉降會導致儲罐上部罐壁發生較大變形，嚴重時會導致浮盤卡盤，影響儲罐的正常運行，甚至造成儲罐結構發生破壞，引發泄漏事故。因此，地基沉降條件下大型儲罐的安全和完整性問題至關重要。

關于地基沉降下大型儲罐安全評價，現行標準API 653—2014[1]、SH/T 3123—2017[2]、SY/T 5921—2017[3]等對儲罐沉降提出了不同的控制要求。評價指標主要有對徑點沉降差、相鄰點沉降差、不均勻沉降等，但標準尚未統一，評價結果也不盡相同。近年來，國內外學者從能直接反映沉降下儲罐變形情況且便于測量的儲罐徑向位移入手進行研究，通過探索變化規律和擬合公式對儲罐沉降安全評價提出建議。陳冰冰等[4]采用千分表和應變計，實驗測量了錐殼圓筒過渡段在內部升壓過程中的應變及徑向位移變化，總結了內壓下薄壁錐殼圓筒過渡段變形特征，為錐殼變形控制準則研究打下基礎。蔣鵬程等[5]通過測試充水過程中罐壁應力的變化開展罐壁靜態應力的試驗研究，證實罐壁上部的抗風圈和加強圈對罐壁徑向位移的控制作用。陳志平等[6]依據彈性板殼理論，對設置了加強圈的儲罐變形進行力學分析，建立起加強圈設置高度和橫截面積大小與罐壁徑向位移間的關系；同時，利用該解析解研究不同加強圈橫截面積和設置高度對油罐壁板危險區域的環向薄膜內力分布和徑向位移的影響。楊志波等[7]開展儲罐在充液靜壓力作用下的靜力分析，得到半罐、滿罐罐壁徑向位移和等效應力的分布及變化規律。MALIK 等[8]、D'ORAZIO 等[9]、KAMYAB等[10]、GODOY等[11]、曹慶帥[12]等學者都對儲罐徑向位移進行了研究，提出或修正了相應準則。但大多數學者在研究時忽略了儲罐幾何參數對不均勻沉降下儲罐結構響應的影響。而研究表明，儲罐幾何參數與儲罐結構響應密切相關，如果對此考慮不足，將導致公式準則適用性變差，從而降低完整性評價方法的可靠性。為了解決上述問題，本文通過建立變參數大型儲罐有限元模型，開展不同敏感參數對地基沉降下儲罐罐頂變形影響的研究，提出一種地基沉降條件下等壁厚儲罐罐頂徑向位移計算方法，可為不均勻沉降下大型儲罐完整性評價提供參考。

1 理論基礎

1.1 傅里葉分解

目前廣泛采用傅里葉分解對儲罐基礎實測沉降數據進行處理，再將處理結果應用于后續研究。在實際沉降觀測中，由布置在罐周基礎外側的若干個水準觀測點測量獲得的罐周實測沉降離散數據，僅能部分反映儲罐基礎的沉降情況，而過多設置水準觀測點又不具有經濟性和實用性。在獲得有限個儲罐基礎實測沉降數據的基礎上，MARR、KAMYAB等[13-14]建議采用傅里葉分解方法對其進行處理，可得到罐周任意一點的近似沉降值和形式簡潔的各階諧波沉降形式。罐周沉降對儲罐結構的影響十分復雜，而對實測沉降進行傅里葉分解后，既可直接研究組合諧波沉降對儲罐的影響，也可先分別研究各階諧波沉降單獨作用時對儲罐的影響，再將得到的結果進行線性疊加，獲得完整的儲罐結構響應。把罐周的實際沉降量u用傅里葉級數進行展開（式1）。

式中：u0為儲罐的整體均勻沉降量，mm；un為各階諧波沉降的幅值，mm；n為諧波沉降的階數；φ為罐周各點所處的角度，rad；φn為各階諧波沉降的初始相位角，rad。

選取某實際儲罐沉降值，對其進行傅里葉分解得到各階諧波沉降幅值和初始相位角（表1），后續作為邊界條件施加在有限元模型上。

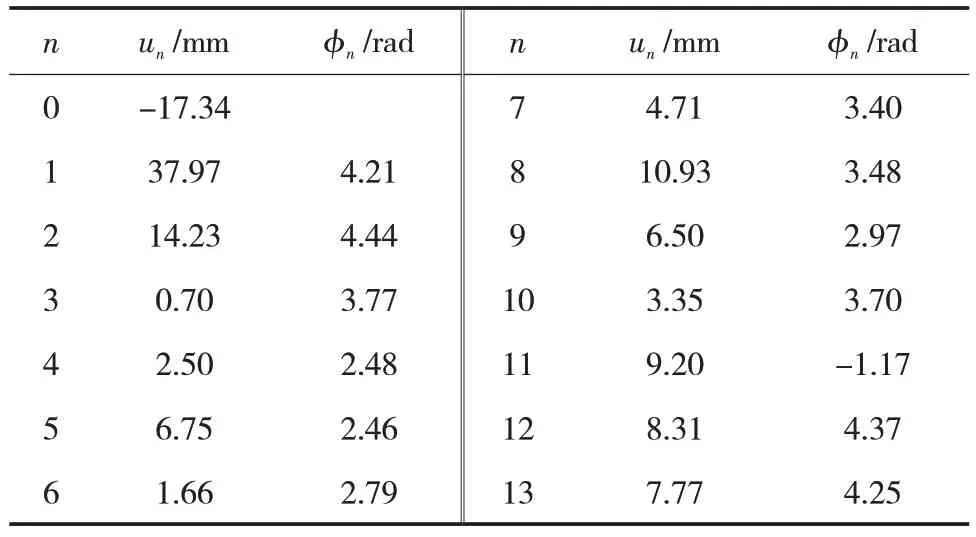
表1 實測沉降傅里葉分解結果Tab.1 Fourier decomposition results of measured settlement

1.2 公式理論解

利用薄膜公式與修正Donnell 公式可推導出等壁厚儲罐罐頂徑向位移公式（式2、式3）。曹慶帥提出了諧波沉降條件下等壁厚儲罐罐頂最大無量綱徑向位移的擬合公式（式4）。

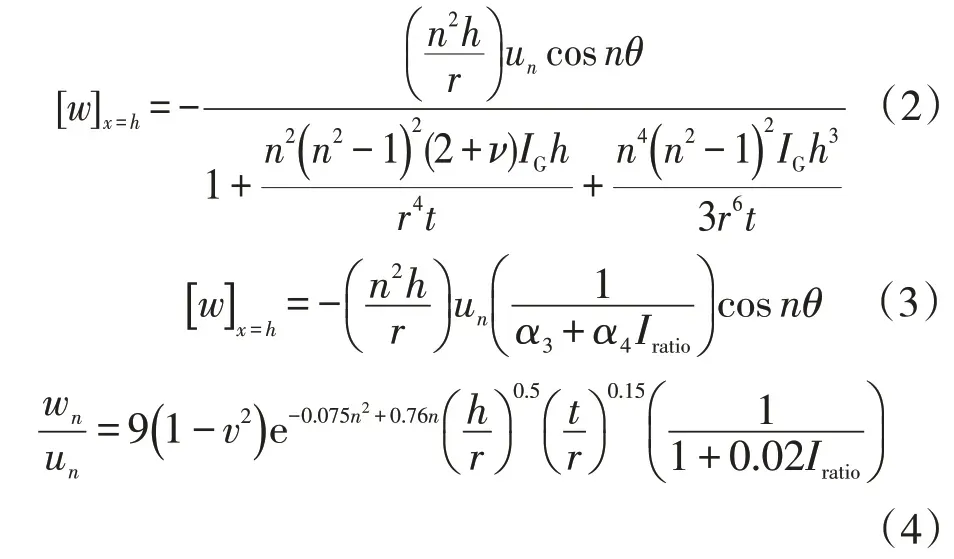
式中：[w]x=h為高度h處罐壁徑向位移，mm；h為儲罐高度，mm；θ為殼體上任一點環向坐標分量，rad；ν為泊松比；r為儲罐半徑，mm；IG為抗風環梁的周向變曲剛度，mm4；t為儲罐罐壁厚度，mm；Iratio為無量鋼參數；wn為n階諧波下罐頂最大徑向位移，mm；

對該儲罐有限元模型分別施加2～12 階諧波沉降，計算得到罐頂最大無量綱徑向位移，并與薄膜理論解、修正Donnell 公式解及曹慶帥提出的擬合公式結果進行對比（圖1）。薄膜理論解僅考慮了殼體的薄膜效應，未考慮殼體的彎曲效應，修正Donnell 公式解則將這兩種效應都考慮在內。因此，在諧波階數較小、殼體彎曲效應表現不明顯時，兩種理論解差距很小；而在諧波階數較大、殼體彎曲效應顯著時，僅有Donnell 公式解能夠真實反映實際情況，薄膜理論解不再適用。學者研究分析表明，儲罐在不均勻沉降下的結構響應與其幾何參數密切相關[15]，因此，利用薄膜公式與修正Donnell公式推導等壁厚儲罐罐頂徑向位移公式從結構角度看不盡合理。曹慶帥提出的擬合公式考慮了儲罐幾何參數，但與兩種理論解及有限元計算結果相差較大。其在進行參數敏感性分析時，選擇的抗風環梁相對剛度范圍為5～60，無法確認該擬合公式在其他條件下的適用性。針對上述情況，需提出一種適用性更好的考慮儲罐幾何參數的等壁厚儲罐罐頂徑向位移計算公式。

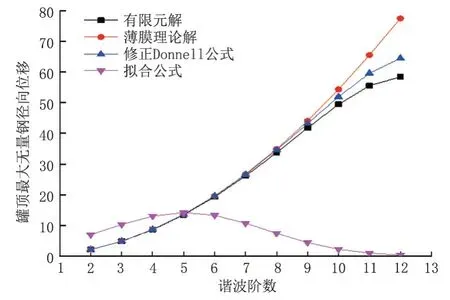
圖1 各公式結果及有限元結果對比Fig.1 Comparison of various formula results and finite element results

2 有限元模型

采用我國某10×104m3大型外浮頂儲罐的結構數據進行儲罐有限元模型建立（圖2）。所選儲罐直徑為80 m，高度為21.7 m，底板的直徑為80.4 m，厚度為20 mm。在儲罐罐壁頂部設有包邊角鋼，尺寸為100 mm×12 mm。建立模型時考慮抗風圈、加強圈（圖3）。假定儲罐所用板材材料為鋼，材料參數為：彈性模量E=2.06×1011Pa，泊松比ν=0.3。有限元模型的邊界條件為：儲罐為空罐；約束儲罐底板的徑向位移及切向位移，防止儲罐發生剛體運動；地基沉降通過在儲罐底板底部施加豎向位移進行模擬，儲罐底板最外側沉降量為處理得到的地基沉降；底板中心點的沉降取最外側沉降的平均值，其余各點的沉降沿半徑方向呈線性變化；模型其余各處均為自由邊界。

圖2 儲罐有限元模型Fig.2 Storage tank finite element model

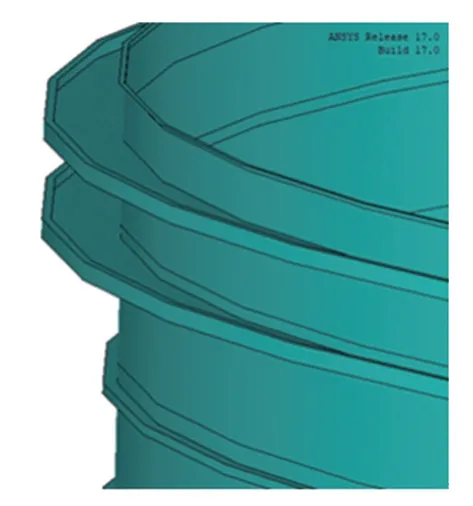
圖3 抗風圈、加強圈結構Fig.3 Structure of wind girder and reinforced ring

為確保計算結果準確性，進行模型正確性驗證。自行設計搭建小型地基沉降儲罐模型實驗裝置1套（圖4），利用升降桿組拉動剛性支撐平臺模擬實際不均勻沉降對儲罐罐壁的影響。儲罐模型直徑為610 mm，高為150 mm，罐壁厚度為0.25 mm，儲罐材料為 304 不銹鋼，彈性模量E=1.95×1011Pa，泊松比ν=0.3。建立與實驗裝置一致的有限元模型。采用實驗時施加的底部位移作為儲罐有限元模型的邊界條件并進行計算分析，將有限元計算結果與實驗結果進行對比（表2），有限元計算結果與實驗結果相對誤差均小于10%。

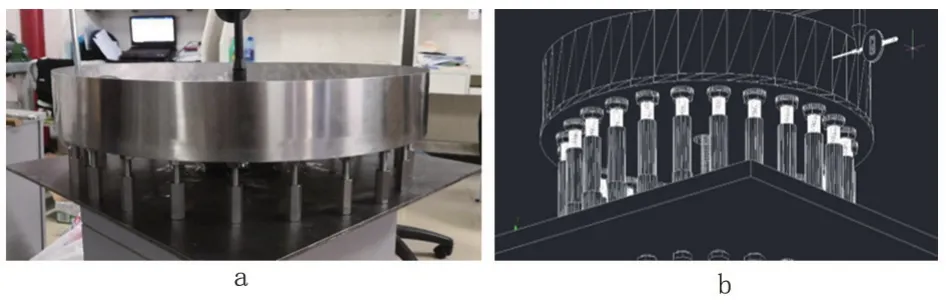
圖4 地基沉降儲罐模型實驗裝置Fig.4 Experimental device of foundation settlement storage tank model

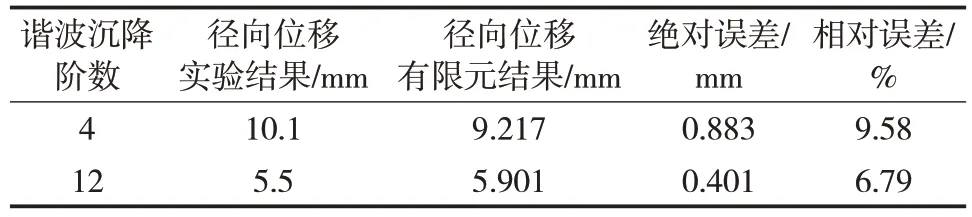
表2 有限元結果與以底部位移作為邊界條件的實驗結果對比Tab.2 Comparison between finite element results and experimental results taking bottom displacement as the boundary condition

MALIK 等也曾在其研究中搭建過小型地基沉降儲罐模型實驗裝置，該裝置中的儲罐模型與所建儲罐有限元模型結構一致但尺寸不同。采用MALIK等實驗時施加的沉降作為儲罐有限元模型的邊界條件并進行計算分析，將有限元計算結果與實驗結果進行對比（表3），有限元計算結果與實驗結果相對誤差均小于10%。綜上所述，儲罐有限元模型可用于后續徑向位移的分析計算及研究。

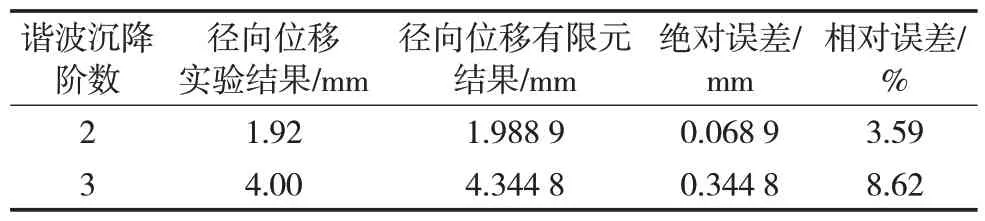
表3 有限元結果與以沉降作為邊界條件的實驗結果對比Tab.3 Comparation between finite element results and experimental results taking settlement as the boundary conditon

3 參數敏感性分析

3.1 高徑比

在保持徑厚比與抗風環梁相對剛度不變的基礎上改變儲罐的高徑比，分別計算各階諧波沉降條件下等壁厚儲罐的罐頂最大無量綱徑向位移（圖5）。在同一高徑比下，當諧波階數在一定范圍內時，儲罐承受階數越高的諧波沉降，越容易產生較大的罐頂徑向位移；當諧波階數進一步增大時，儲罐對諧波沉降的敏感性開始下降。高徑比較大儲罐對6～8 階諧波沉降更為敏感，承受6～8 階諧波沉降時更易產生較大的罐頂徑向位移；而高徑比較小儲罐則對10～12 階諧波沉降更為敏感，承受10～12 階諧波沉降時更易產生較大的罐頂徑向位移。

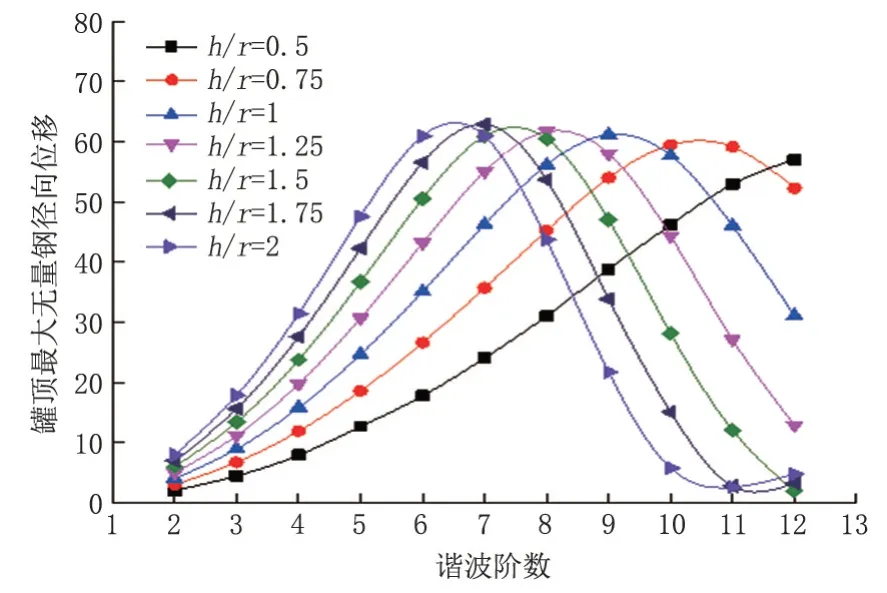
圖5 不同高徑比下罐頂最大無量綱徑向位移Fig.5 Maximum dimensionless radial displacement of tank top under different height-diameter ratios

3.2 徑厚比

在保持高徑比與抗風環梁相對剛度不變的基礎上改變儲罐的徑厚比，分別計算各階諧波沉降條件下等壁厚儲罐的罐頂最大無量綱徑向位移（圖6）。在同一徑厚比下，當儲罐徑厚比較小時，罐頂最大無量綱徑向位移存在極大值；而當儲罐徑厚比較大時，諧波沉降階數對罐頂變形的影響變為單調遞增關系，諧波沉降的階數越高，對罐頂變形的影響越大。儲罐徑厚比會在一定程度上影響儲罐對諧波沉降的敏感程度，徑厚比較小儲罐對9～11 階諧波沉降更為敏感，承受9～11 階諧波沉降時更易產生較大的罐頂徑向位移；而徑厚比較大儲罐對12 階諧波沉降更為敏感，并且此特性不再隨徑厚比的改變而變化。

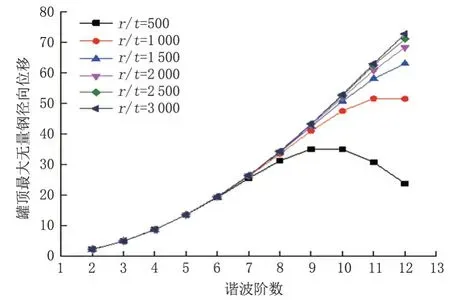
圖6 不同徑厚比下罐頂最大無量綱徑向位移Fig.6 Maximum dimensionless radial displacement of tank top under different diameter-thickness ratios

3.3 抗風環梁相對剛度

在保持高徑比與徑厚比不變的基礎上改變儲罐的抗風環梁相對剛度，分別計算各階諧波沉降條件下等壁厚儲罐的罐頂最大無量綱徑向位移（圖7）。在同一抗風環梁相對剛度下，當諧波階數在一定范圍內時，儲罐承受的諧波沉降階數越高，越容易產生較大的罐頂徑向位移；而當諧波階數進一步增大時，儲罐對諧波沉降的敏感性開始下降，不同抗風環梁相對剛度的儲罐對諧波沉降階數的敏感程度是不一樣的，但總體上都對較高階數的諧波沉降更為敏感。隨著儲罐抗風環梁相對剛度的增大，罐頂最大無量綱徑向位移都單調遞減，即諧波沉降條件下抗風環梁相對剛度較大的儲罐抵抗罐頂變形的能力較強。

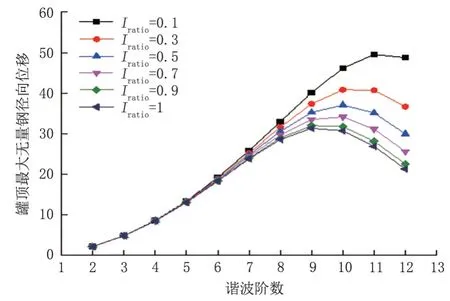
圖7 不同抗風環梁相對剛度下罐頂最大無量綱徑向位移Fig.7 Maximum dimensionless radial displacement of tank top under relative stiffness of different wind resistant ring beams

4 罐頂最大徑向位移計算方法

由圖5 至圖7 可知，高徑比、徑厚比、儲罐抗風環梁相對剛度對諧波沉降條件下儲罐罐頂變形具有顯著影響。在提出地基沉降條件下等壁厚儲罐罐頂徑向位移計算方法時，需將高徑比、徑厚比、儲罐抗風環梁相對剛度皆考慮在內，以保證計算方法的可靠性。回歸得到諧波沉降條件下等壁厚儲罐罐頂最大無量綱徑向位移擬合公式（式5）。

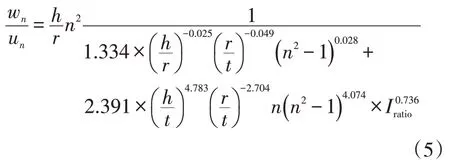
將不同情況下該擬合公式計算得出的罐頂最大無量綱徑向位移與有限元結果進行對比（圖8），可以看出擬合公式計算結果與有限元結果吻合較好。

將式（5）進行變換可得到諧波沉降條件下等壁厚儲罐罐頂徑向位移公式（6）。

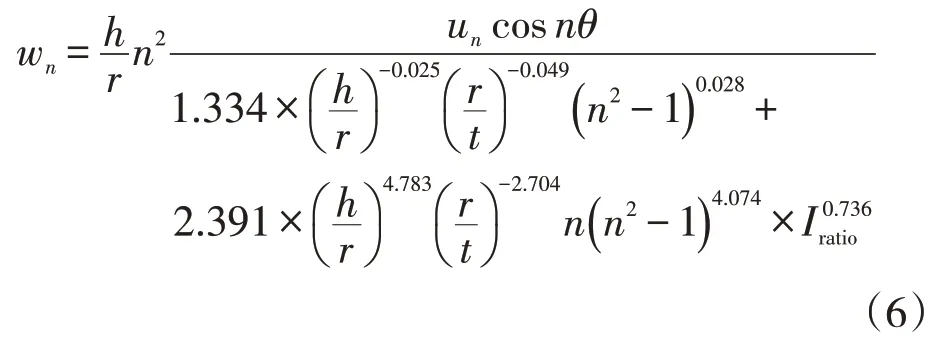
將各階諧波沉降作用下的罐頂徑向位移公式疊加，即可得到沉降作用下罐頂任意位置徑向位移預測值式（7）。

式中：w為實際沉降作用下的罐頂任意位置徑向位移預測值，mm；N為儲罐沉降周邊測點個數。

5 結論

儲罐地基不均勻沉降會影響儲罐安全運行。通過建立大型儲罐數值仿真模型，研究了儲罐高徑比、徑厚比、抗風環梁相對剛度等參數對儲罐結構變形的影響規律，提出了不均勻沉降下大型儲罐罐頂徑向位移預測方法，并由此得出以下結論：

（1）數值仿真計算結果與模型實驗結果吻合較好，表明數值仿真是不均勻儲罐地基沉降罐壁變形計算的可靠手段。

（2）在同一高徑比下，罐頂徑向位移隨諧波階數的增大而先增大后減小。在同一徑厚比下，徑厚比較小時罐頂最大無量綱徑向位移存在極大值；當徑厚比較大時，諧波沉降階數對罐頂變形的影響變為單調遞增關系。在同一抗風環梁相對剛度下，罐頂徑向位移隨諧波階數的增大而先增大后減小。

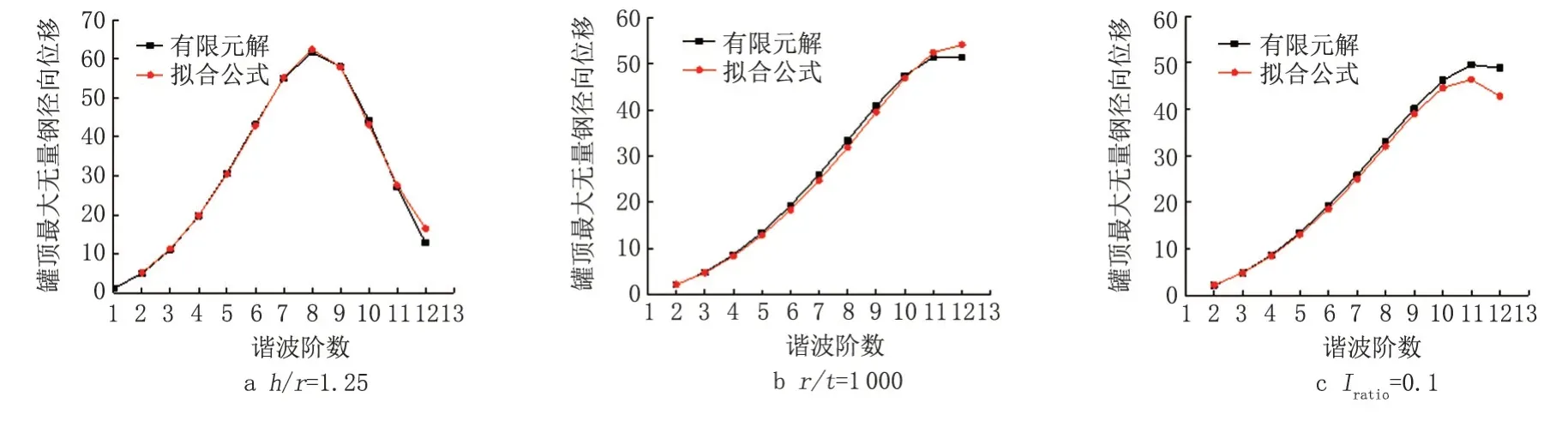
圖8 預測方法與有限元結果對比Fig.8 Comparison of prediction methods and finite element results

（3）高徑比、徑厚比、儲罐抗風環梁相對剛度等敏感參數對諧波沉降條件下儲罐罐頂變形具有顯著影響，提出地基沉降條件下大型儲罐罐頂徑向位移預測方法，綜合考慮了高徑比、徑厚比、儲罐抗風環梁相對剛度等參數的影響。

（4）經對比，本文提出的綜合考慮儲罐高徑比、徑厚比及抗風環梁相對剛度等參數的罐頂位移預測方法，可以得到較為準確的結果，為地基不均勻沉降下大型儲罐完整性評價提供參考。