一種小波閾值函數(shù)構(gòu)建的圖像去噪算法研究
萬(wàn)莊姝,譚碧瑩,段雅倩,閔鋼,舒忠,
(1.荊楚理工學(xué)院,荊門(mén)448001;2.荊門(mén)日?qǐng)?bào)社荊門(mén)新聞網(wǎng),荊門(mén)448000)
0 引言
當(dāng)今,針對(duì)圖像處理的應(yīng)用已涉及眾多領(lǐng)域,特別是圖像識(shí)別和人工智能等方面,圖像處理都是重要的組成環(huán)節(jié)和重要基礎(chǔ)。圖像中的噪聲嚴(yán)重影響到了圖像識(shí)別或人工智能等技術(shù)應(yīng)用,在這些技術(shù)應(yīng)用中,圖像邊緣檢測(cè)是最重要的處理過(guò)程之一,是圖像增強(qiáng)[1-2]、圖像分割[3-4]等處和圖像特征分類(lèi)[5-6]、圖像特征提取[7]等處理的關(guān)鍵,噪聲所造成的影響都具有較強(qiáng)的破壞性,因此,圖像去噪具有較高的研究和實(shí)用價(jià)值。
在圖像去噪處理中,需要考慮的主要因素是在去除噪聲的同時(shí),必須確保圖像自己具有特征的完整性,這些特征主要包括:圖像邊緣輪廓信息、圖像紋理信息和圖像色彩等。因此,在圖像去噪處理方法的應(yīng)用也特別重要。針對(duì)不同的噪聲種類(lèi)[8-9],在已有的圖像去噪方法中,一些濾波算法可以有效地去除噪聲,但對(duì)圖像的邊緣信息和紋理信息都會(huì)產(chǎn)生不同程度的破壞;一些濾波算法則雖然可以有效保護(hù)圖像的正常信息,但去噪效果不理想,很難將圖像中的高頻信息全部準(zhǔn)確分離出來(lái);一些算法對(duì)某一種噪聲去除效果良好,但其他噪聲則無(wú)能為力;還有一些得法運(yùn)算效率不高,等等。
小波圖像去噪方法的提出,其主要依據(jù)是圖像經(jīng)過(guò)小波變換后,可以通過(guò)小波系數(shù)對(duì)圖像進(jìn)行稀疏性描述,將圖像的組成信息進(jìn)行分割,將屬于噪聲的信息分離出來(lái)。其中,屬于噪聲的信息其小波系數(shù)通常都偏小,通過(guò)設(shè)置系數(shù)閾值,獲取圖像中的噪聲信息就不是難事。采用小波閾值法去除圖像噪聲,關(guān)鍵的兩步是:首先構(gòu)建小波閾值函數(shù),然后通過(guò)閾值函數(shù)計(jì)算出閾值。目前,主要小波閾值去噪方法中,常用的是軟閾值去噪函數(shù)[10]和硬閾值去噪函數(shù)[11]兩類(lèi)。小波閾值去噪,首先需要對(duì)圖像進(jìn)行小波變換,并對(duì)變換后的小波系數(shù)進(jìn)行統(tǒng)計(jì),依據(jù)小波系數(shù)的統(tǒng)計(jì)結(jié)果,以閾值函數(shù)計(jì)算的閾值的衡量標(biāo)準(zhǔn),對(duì)直接進(jìn)行小波變換后的小波系數(shù)進(jìn)行調(diào)整,調(diào)整的主要原則是盡量多地將小波系數(shù)置為零,并用于圖像去噪處理,調(diào)整后的小波系數(shù)集合,決定了圖像的去噪效果。軟閾值圖像去噪方法是將多數(shù)的小波系數(shù)進(jìn)行置零處理,應(yīng)用于圖像去噪處理中,是否置零依據(jù)閾值大小決定。硬閾值去噪方法則是通過(guò)與閾值進(jìn)行比較,對(duì)高于閾值的小波系數(shù)不作任何處理,而小于閾值的小波系數(shù)全部置為零,再將調(diào)整后的小波系數(shù)應(yīng)用于圖像去噪處理中。基于以上小波閾值去噪策略,研究人員對(duì)此也進(jìn)行了一系列的研究與實(shí)驗(yàn)。
在小波圖像去噪中,閾值的選取起到了決定性的作用,閾值的大小控制至關(guān)重要。閾值大了,則小波系數(shù)大部分會(huì)被置零,圖像中有效的信息就會(huì)作為噪聲被處理掉;閾值小了,則小波系數(shù)少部分會(huì)被置零,圖像中的噪聲信息不可能全部被選出來(lái)。在已有的閾值計(jì)算方法中,有固定一個(gè)閾值和多閾值兩種方法,在多閾值選取方法中,又分為頻率分割閾值確定與空間分割閾值確定。頻率分割閾值是直接在圖像小波頻率域?qū)D像小波系數(shù)的組成集合進(jìn)行分類(lèi),分類(lèi)結(jié)果有幾組,則閾值就有幾個(gè);空間分割閾值是對(duì)小波頻率域?qū)?yīng)的圖像空間,進(jìn)行小波系數(shù)的組成集合分類(lèi),同樣是分類(lèi)結(jié)果有幾組,則閾值就有幾個(gè)。兩種多閾值方法,都具有一定的自適應(yīng)圖像去噪閾值控制功能。
圖像的去噪過(guò)程,是一個(gè)對(duì)最理想圖像的預(yù)估為基礎(chǔ)的處理過(guò)程,在理論上,要想得到完整無(wú)缺的效果是根本不可能的,這是圖像去噪的主要難點(diǎn)所在。同時(shí),圖像去噪處理還涉及到一個(gè)圖像噪聲判定問(wèn)題。去噪方法有選擇,還需要考慮到噪聲類(lèi)型和噪聲信息在圖像中的分布問(wèn)題,特別找出噪聲信息在圖像中的分布特征尤為重要。因此,噪聲模型的建構(gòu)也是圖像的去噪重要環(huán)節(jié),圖像去噪處理主要是依托相應(yīng)的噪聲模型進(jìn)行實(shí)驗(yàn),獲取一些有效的去噪處理方法。當(dāng)前,噪聲模型的定義,主要針對(duì)一些細(xì)微因素進(jìn)行構(gòu)建,重點(diǎn)是對(duì)噪聲的分布進(jìn)行描述,較為典型的噪聲模型有:高斯分布模型、高斯與分辨率混合分布模型、高斯與拉普拉斯混合分布模型等[12-14]。依據(jù)這些噪聲模型,在進(jìn)行圖像去噪處理中,也面臨著諸如:閾值函數(shù)和閾值的最佳選擇、多種混合噪聲的去除、需要進(jìn)行噪聲模型構(gòu)建與驗(yàn)證等難題。
由于小波變換所構(gòu)建的閾值函數(shù)在閾值處是連續(xù)的,可以防止圖像處理中出現(xiàn)新的噪聲,并以線性公式構(gòu)建閾值函數(shù),可以有效防止閾值偏差。本文以加性高斯和乘性斑點(diǎn)兩種典型圖像噪聲為研究目標(biāo),通過(guò)對(duì)頻域圖像去噪算法的原理進(jìn)行分析,以小波變換為基礎(chǔ)平臺(tái),通過(guò)構(gòu)建小波閾值函數(shù),獲取精確閾值,最終實(shí)現(xiàn)圖像去噪算法的設(shè)計(jì)。
1 小波頻域去噪原理
在小波變換中,小波的主要參量是時(shí)間變化量和頻率變化量,時(shí)間變化量是指截獲圖像中第一個(gè)時(shí)間段內(nèi)或第二個(gè)時(shí)間段內(nèi)的變化量;頻率變化量是指截獲圖像在第一個(gè)時(shí)間段內(nèi)中變化比較慢的信息,也就是圖像中的低頻率信息,或者是截獲圖像在第一個(gè)時(shí)間段內(nèi)中變化比較快的信息,也就是圖像中的高頻率信息。
圖像小波變換的基本原理是以時(shí)間變化參量和頻率變化參量為主體,構(gòu)建一個(gè)族函數(shù),應(yīng)用這個(gè)族函數(shù)去表示(或最大程度接近)圖像信息集合,并對(duì)獲取的圖像信息集合進(jìn)行頻率分類(lèi)(低頻率或高頻率)和分析。小波變換可以表示隨著時(shí)間變化而具備的圖像頻率特性,可以進(jìn)一步準(zhǔn)確描述圖像的邊緣信息,這在傅里葉變換中是不能或難于實(shí)現(xiàn)的。
設(shè)f(t)∈L2(R),ψ(t)為基本小波函數(shù),其連續(xù)小波變換公式為[15]:

圖像通過(guò)離散小波變換后,具備可分解性可以充分應(yīng)用于本文提出的小波閾值函數(shù)去噪算法中。
2 本文小波閾值函數(shù)去噪算法實(shí)現(xiàn)
2.1 小波閾值的預(yù)估
依據(jù)以上對(duì)小波去噪原理的分析,小波圖像去噪的關(guān)鍵是對(duì)閾值的預(yù)估。閾值預(yù)估必須遵循一定的規(guī)則,在最基本的閾值選取規(guī)則中,Sqtwolog 通用閾值、BayesShrink 貝葉斯閾值和最大最小值Miniman 閾值三種選取規(guī)則是進(jìn)行小波去噪閾值構(gòu)建的研究與應(yīng)用基礎(chǔ)。
Sqtwolog 通用閾值的定義是:

其中,M×N為圖像的維度,σ為噪聲標(biāo)準(zhǔn)差。該閾值的預(yù)估條件為噪聲的小波系數(shù)呈現(xiàn)高斯正態(tài)分布。
BayesShrink 貝葉斯閾值的定義是TB=σ2σg,其中,σ2為噪聲方差,σg為噪聲高斯標(biāo)準(zhǔn)差。該閾值的預(yù)估條件為噪聲的小波系數(shù)呈現(xiàn)高斯分布。
最大最小值Miniman 閾值的定義是:

其中,σ為噪聲標(biāo)準(zhǔn)差,k為小波系數(shù)的個(gè)數(shù)。該閾值是對(duì)Sqtwolog 通用閾值的改進(jìn)。
2.2 小波閾值函數(shù)的構(gòu)建
小波閾值函數(shù)的作用是對(duì)小波系數(shù)進(jìn)行運(yùn)算,硬閾值函數(shù)、軟閾值函數(shù)和半軟半硬閾值函數(shù)是最基本的小波閾值函數(shù)[15]。
硬閾值圖像去噪是對(duì)小波系數(shù)進(jìn)行處理的規(guī)則是:對(duì)小波系數(shù)值偏小的系數(shù)全部設(shè)置為零,小波系數(shù)值偏大的系數(shù)值則保持不變。依據(jù)離散小波變換和小波分解變換原理,硬閾值函數(shù)可以定義為:

其中,j為圖像頻率變化范圍取值,k為小波系數(shù)的個(gè)數(shù),T(j,k)為理想閾值,T為預(yù)估閾值。
硬閾值圖像去噪不會(huì)破壞圖像的邊緣信息,但硬閾值函數(shù)不具有連續(xù)性,在處理過(guò)程中會(huì)產(chǎn)生新的圖像噪聲。
軟閾值圖像去噪是對(duì)小波系數(shù)進(jìn)行處理的規(guī)則是:對(duì)小波系數(shù)值偏小的系數(shù)全部設(shè)置為零,小波系數(shù)值偏大的系數(shù)值則依據(jù)連續(xù)性平緩地接近于零,也就是偏大的系數(shù)值在原有值的基礎(chǔ)上會(huì)依次逐漸進(jìn)行減小處理。同樣依據(jù)前文介紹的離散小波變換和小波分解變換原理,軟閾值函數(shù)可以定義為:

(sign 表示不可求導(dǎo)函數(shù))。軟閾值圖像去噪所構(gòu)建的閾值函數(shù)具有平滑的連續(xù)性,但強(qiáng)制性對(duì)原有小波變換的較大的系數(shù)值進(jìn)行了減小,必須會(huì)造成小波變換后圖像中的部分高頻信息被忽略,引起的結(jié)果是對(duì)圖像的邊緣信息進(jìn)行了破壞。
由于硬閾值圖像去噪和軟閾值圖像去噪都具有一定的缺陷,因此,出現(xiàn)了半軟半硬閾值去噪方法。半軟半硬閾值去噪方法的關(guān)鍵是在軟閾值函數(shù)的基礎(chǔ)上,對(duì)預(yù)估閾值T進(jìn)行了門(mén)限控制,其門(mén)限控制參數(shù)為λ,半軟半硬閾值函數(shù)可以定義為:

在公式(7)中,當(dāng)λ=0 時(shí),T?(j,k)則為硬閾值函數(shù);當(dāng)λ=0 時(shí),T?(j,k)則為軟閾值函數(shù)。引入該策略的主要目的是確保圖像在處理過(guò)程中邊緣信息不會(huì)被作為噪聲被剔除,又不會(huì)在處理過(guò)程中產(chǎn)生新的噪聲。但是,針對(duì)不同的圖像在經(jīng)過(guò)小波變換后,受到圖像信息本身存在的不定因素,加之半軟半硬閾值在接受了一些優(yōu)點(diǎn)的同時(shí),并不能完全摒棄硬閾值和軟閾值處理中的缺陷,影響圖像在人眼中的視覺(jué)感受是必然存在的。
根據(jù)以上對(duì)三種基本的小波閾值函數(shù)去噪處理原理進(jìn)行分析,總結(jié)了各自存在的問(wèn)題。在此基礎(chǔ)上,結(jié)合以上三種方法的優(yōu)點(diǎn),本文將進(jìn)一步對(duì)基本的小波閾值函數(shù)進(jìn)行改進(jìn)展開(kāi)研究。
本文構(gòu)建小波閾值函數(shù)的主要思想是:構(gòu)建的閾值函數(shù)要在其閾值處具有連續(xù),目的是防止圖像出現(xiàn)新的噪聲。以最基本的、結(jié)構(gòu)最簡(jiǎn)單的線性方程f(x)=x為基礎(chǔ),建立閾值函數(shù)的線性變化標(biāo)準(zhǔn),使小波系數(shù)平緩地接近零值,防止去噪閾值出現(xiàn)有等級(jí)區(qū)分的偏差,并努力控制閾值偏差出現(xiàn)累加性。在噪聲與有效的圖像信息之間進(jìn)行有效的平滑處理,實(shí)現(xiàn)兩者之間的自然融合,這也是因?yàn)槿魏我环N噪聲在預(yù)估去噪策略下,在理論上根本無(wú)法實(shí)現(xiàn)對(duì)噪聲進(jìn)行根除;同時(shí),無(wú)論對(duì)圖像進(jìn)行何種處理,在處理完成后,產(chǎn)生新的噪聲是不可避免的。為了對(duì)圖像中的噪聲進(jìn)行更為細(xì)致的分離,同時(shí)確保在計(jì)算閾值的過(guò)程中能夠?qū)崿F(xiàn)自主調(diào)整,所構(gòu)建的閾值函數(shù)必然能夠進(jìn)行微分運(yùn)算。為了確保以上思想能夠?qū)崿F(xiàn),結(jié)合離散小波變換和小波分解變換的應(yīng)用,本文設(shè)計(jì)的小波閾值函數(shù)可以定義為:

在公式(8)中,j為圖像頻率變化范圍取值,k為小波系數(shù)的個(gè)數(shù),a和b分別為理想閾值T(j,k)與預(yù)估閾值T或-T大小比較的系數(shù),系數(shù)a表示大于預(yù)估閾值,系數(shù)b表示小于預(yù)估閾值,0.5×λ為小波平緩系數(shù),sgn 表示可求導(dǎo)函數(shù)。從公式中可以看出,當(dāng)λ=0時(shí),可表示為軟閾值函數(shù),當(dāng)λ的取值逐漸接近0 時(shí),閾值函數(shù)也更接近于軟閾值函數(shù);當(dāng)λ=1 時(shí),系數(shù)0.5則還能起到平滑過(guò)度的作用,當(dāng)然,在λ≠0 的一定取值范圍內(nèi),同樣可以起到平滑作用,且有助于求導(dǎo)計(jì)算。
本文設(shè)計(jì)的閾值函數(shù),在理想閾值T(j,k)和預(yù)估閾值±T相等處都具有連續(xù)性。在|T(j,k)| 的值增加時(shí)(也就是小波系數(shù)大于預(yù)估閾值T時(shí)),函數(shù)f(T(j,k))的值也越接近理想閾值T(j,k),其所具有的線性特征,確保了閾值變化中不會(huì)出現(xiàn)偏差現(xiàn)象。由于構(gòu)建的閾值函數(shù)參量有所增加,而函數(shù)可以實(shí)現(xiàn)微分計(jì)算就可以簡(jiǎn)化因參量過(guò)多造成的計(jì)算復(fù)雜度,在預(yù)估閾值T處進(jìn)行微分計(jì)算的前提有兩個(gè):一是理想閾值T(j,k)和預(yù)估閾值±T相等處連續(xù)(該條件已獲得);二是函數(shù)可以進(jìn)行求導(dǎo)計(jì)算。通過(guò)計(jì)算,當(dāng)b=(0.5×λ)-a時(shí),構(gòu)建的閾值函數(shù)就可以進(jìn)行微分計(jì)算。因此,通過(guò)控制公式中的參量λ和a,就可以得到最佳的圖像去噪閾值函數(shù)。
3 實(shí)驗(yàn)及分析
3.1 閾值處平滑性驗(yàn)證
在進(jìn)行圖像去噪效果驗(yàn)證前,首先以線性方程f(x)=x為分析比較基礎(chǔ),對(duì)軟閾值函數(shù)、硬閾值函數(shù)和本文設(shè)計(jì)的小波閾值函數(shù)在閾值處所具有的連續(xù)性進(jìn)行比較,將其設(shè)置為實(shí)驗(yàn)1。實(shí)驗(yàn)1 的方法是:將預(yù)估閾值和計(jì)算閾值設(shè)定為[-20,+20]之間,將預(yù)估閾值定義為x,將計(jì)算閾值定義為f(x),分別應(yīng)用軟閾值函數(shù)、硬閾值函數(shù)和本文設(shè)計(jì)的小波閾值函數(shù)對(duì)f(x)進(jìn)行計(jì)算,在計(jì)算結(jié)果所形成的直線、折線或曲線中,首先比較f(x)與x所對(duì)應(yīng)的值是否接近,然后比較在f(x)與x所對(duì)應(yīng)的值有較大誤差時(shí),其對(duì)應(yīng)值的差距有多大。比較結(jié)果的評(píng)判方法是f(x)與x所對(duì)應(yīng)的值越接近,其處理效果所具有的平滑過(guò)度特征非常直接;在f(x)與x所對(duì)應(yīng)的值存在差距時(shí),其差距值越小,可以表明其處理效果所具有向平滑過(guò)度特征方向控制的意識(shí)。另外,三種方法輸出的線性結(jié)果圖示中,在f(x)與x所對(duì)應(yīng)的值存在差距的區(qū)域中,如果輸出結(jié)果是由直線和折線組成的線段,可以表明其處理結(jié)果平滑過(guò)度特征不明顯(或者說(shuō)是根本不具備平滑過(guò)度特征);如果輸出結(jié)果是由曲線組成的,則可以表明其處理結(jié)果具有平滑過(guò)度特征。實(shí)驗(yàn)1 所輸出的比較結(jié)果如圖1 所示。

圖1
圖1 為使用硬閾值函數(shù)、軟閾值函數(shù)和本文設(shè)計(jì)的小波閾值函數(shù)經(jīng)過(guò)線性處理后的輸出結(jié)果比較圖。
在圖1 中,本文設(shè)計(jì)的小波閾值函數(shù)進(jìn)行線性處理后的輸出為曲線,可以充分地表示在閾值處具有平滑過(guò)度特征;硬閾值函數(shù)和軟閾值函數(shù)經(jīng)過(guò)線性處理后的輸出均為折線閾值處的處理明顯具有生硬性。
3.2 去噪效果驗(yàn)證
實(shí)驗(yàn)選取三幅圖像(均為灰度圖像)進(jìn)行MATLAB仿真實(shí)驗(yàn),首先通過(guò)前文介紹的圖像復(fù)原原理,構(gòu)建一個(gè)加性高斯噪聲和乘性斑點(diǎn)噪聲混合的退化模型;然后依據(jù)前文論述的硬閾值圖像去噪算法、半軟半硬閾值去噪圖像算法和本文提出的圖像去噪算法原理,分別提取三幅出圖像中的低、高頻信息,最后以峰值信噪比(PSNR)為評(píng)價(jià)參數(shù),對(duì)三種圖像去噪方法進(jìn)行比較分析,驗(yàn)證本文提出的圖像去噪方向的優(yōu)勢(shì)所在。實(shí)驗(yàn)2 通過(guò)MATLAB 仿真效果如圖2 所示。

圖2 對(duì)三幅圖像采用三種去噪方法的效果比較
在圖2 中,加性高斯噪聲和乘性斑點(diǎn)噪聲對(duì)三幅原稿圖像的影響都非常明顯,對(duì)于去噪效果的比較,本文提出的去噪算法效果最好,硬閾值去噪效果最差。實(shí)驗(yàn)中還使用PSNR 作為圖像去噪效果的客觀評(píng)價(jià)參數(shù)[29],其MATLAB 仿真實(shí)驗(yàn)獲取參量見(jiàn)表1 所示。

表1 三種去噪算法的PSNR 參數(shù)比較表
以上實(shí)驗(yàn)從主觀和客觀兩個(gè)方面進(jìn)行比較都表明:在本文提出的算法具有良好的圖像去噪效果。其中,測(cè)試圖像本文算法處理結(jié)果與對(duì)應(yīng)原稿基本相似,半軟半硬閾值去噪算法也與對(duì)應(yīng)原稿基本相似,但硬閾值去噪算法明顯與原稿存在差別,去噪效果不徹底。通過(guò)使用峰值信噪比進(jìn)行仿真實(shí)驗(yàn),本文算法處理結(jié)果獲取的參數(shù)值更接近理想值(30.00-32.00),同樣,半軟半硬閾值去噪算法也優(yōu)于硬閾值去噪算法。
3.3 邊緣提取效果驗(yàn)證
本文為了進(jìn)一步驗(yàn)證本文圖像去噪算法的效果。實(shí)驗(yàn)方法是:選取與實(shí)驗(yàn)2 一致的三幅原稿圖像進(jìn)行MATLAB 仿真實(shí)驗(yàn),圖像邊緣提取采用二維Otsu 算法[30],以處理效率的檢測(cè)結(jié)果作為為評(píng)價(jià)依據(jù),對(duì)硬閾值圖像去噪、半軟半硬閾值圖像去噪和本文圖像去噪方法進(jìn)行去噪后,使用二維Otsu 算法進(jìn)行邊緣特征提取,評(píng)價(jià)實(shí)驗(yàn)2 中三種圖像去噪方法的高效性和優(yōu)良性。三種圖像邊緣特征提取方法的測(cè)試結(jié)果如圖3 所示,表2 為使用三種圖像去噪算法后進(jìn)行邊緣特征提取的運(yùn)算時(shí)間對(duì)比表。

圖3 使用三種圖像去噪處理后對(duì)圖像邊緣特征進(jìn)行提取的測(cè)試結(jié)果
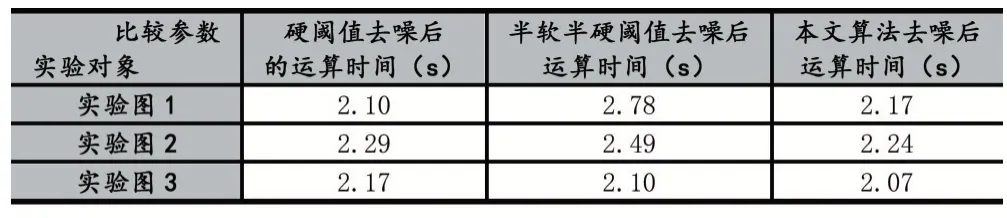
表2 使用三種圖像去噪算法后進(jìn)行邊緣特征提取的運(yùn)算時(shí)間對(duì)比表
以上實(shí)驗(yàn)比較結(jié)果表明:使用本文算法進(jìn)行圖像去噪后,其邊緣特征提取的效果優(yōu)于另外兩種,其運(yùn)行效率結(jié)果相近。其中,使用本文算法進(jìn)行圖像去噪后,其邊緣特征提取所保留的圖像邊緣細(xì)節(jié)最為豐富;使用半軟半硬閾值去噪后,邊緣特征提取所保留的圖像邊緣細(xì)節(jié),要優(yōu)于硬閾值圖像去噪后的邊緣特征提取效果。三種方法進(jìn)行的圖像邊緣特征提取處理時(shí)間相近,主要原因是所采用的邊緣特征提取方法完全相同,也說(shuō)明了無(wú)論采用什么方法進(jìn)行圖像去噪處理,后續(xù)的圖像特征提取在處理效率方面沒(méi)有明顯的區(qū)別,表2 統(tǒng)計(jì)的數(shù)據(jù)意義并不大。
4 結(jié)語(yǔ)
本文通過(guò)對(duì)小波圖像去噪算法進(jìn)行分析,以噪聲模型構(gòu)建為基礎(chǔ),根據(jù)小波閾值函數(shù)的運(yùn)算原理,提出了基于硬閾值、軟閾值和半軟半硬閾值結(jié)合的圖像去噪算法,構(gòu)建的小波閾值函數(shù)具有四個(gè)特點(diǎn),通過(guò)三個(gè)角度進(jìn)行實(shí)驗(yàn)分析,結(jié)果表明本文算法具有一定的優(yōu)勢(shì)。本文研究的主要工作包括:
(1)構(gòu)建小波閾值去噪是依據(jù)預(yù)估的閾值進(jìn)行運(yùn)算的,其處理過(guò)程想達(dá)到完全去除圖像中的噪聲很難實(shí)現(xiàn)。
(2)小波閾值圖像去噪的流程為:帶噪聲的圖像進(jìn)行小波正變換→完成小波頻率分解→構(gòu)建小波閾值函數(shù)→使用閾值函數(shù)對(duì)小波系數(shù)進(jìn)行處理→對(duì)處理后的圖像進(jìn)行小波逆變換→重構(gòu)建變換后的圖像,得到去噪后的圖像。
(3)小波閾值函數(shù)的構(gòu)建,在閾值處具有連續(xù)性的條件,是防止圖像出現(xiàn)新噪聲的有效方法。
(4)以線性方程為基礎(chǔ),建立閾值函數(shù)的線性變化標(biāo)準(zhǔn),可以防止去噪閾值出現(xiàn)有等級(jí)區(qū)分的偏差。
(5)在噪聲與圖像信息之間進(jìn)行有效的平滑處理,可以將一些無(wú)法去除的噪聲無(wú)影響(或小影響)地融入圖像中。
(6)在小波域?qū)崿F(xiàn)圖像去噪處理,確保小波閾值函數(shù)可以進(jìn)行微分運(yùn)算,是簡(jiǎn)化運(yùn)算量和確保閾值自主調(diào)整的重要前提。
- 現(xiàn)代計(jì)算機(jī)的其它文章
- 基于多實(shí)例學(xué)習(xí)的醫(yī)療圖像識(shí)別研究進(jìn)展
- 基于Unity 的《AR 槍械》的設(shè)計(jì)與實(shí)現(xiàn)
- 基于Hue 的自動(dòng)化數(shù)據(jù)分析系統(tǒng)設(shè)計(jì)與實(shí)現(xiàn)
- 智能語(yǔ)音機(jī)器人前端語(yǔ)音處理系統(tǒng)的設(shè)計(jì)及實(shí)現(xiàn)
- 學(xué)生社區(qū)智慧門(mén)禁管理系統(tǒng)的設(shè)計(jì)和實(shí)現(xiàn)
- 五子棋游戲雙人對(duì)決的設(shè)計(jì)與實(shí)現(xiàn)

