基于損傷一致性的動車組轉向架載荷實驗譜研究1)

鄒驊 吳奇峰 孫守光

(北京交通大學機械與電子控制工程學院,北京 100044)

引言

對于機械產品而言,載荷問題是事關結構可靠性研究和疲勞壽命評價的重要問題[1-2].軌道車輛結構載荷問題近幾十年持續得到研究[3-5].高速列車轉向架構架是安置于車體和輪對之間的傳力裝置[6],其載荷研究對于確保高速列車營運安全至關重要.

關于轉向架構架結構載荷的研究已有諸多文獻發表.文獻[7-8]采用靜態載荷乘以載荷因子的方法計算得到構架結構載荷.文獻[9]采用截斷奇異值法構建了構架應力和載荷之間的傳遞關系矩陣.文獻[10-12]將部分實測數據引入多體動力學仿真模型得到基于多工況的結構載荷時間歷程.金新燦等[13]基于單節車輛通過道岔時的多體系統(MBS) 模型,采用剛柔耦合動力學仿真的方法得到車輛通過道岔時關鍵部件的動態載荷.Matsumoto 等[14]借助高精度轉向架滾動試驗臺對新研發的轉向架實施曲線性能試驗,研究表明試驗臺所得結果與數值仿真及實際線路運行結果具有良好的一致性.文獻[15]針對應用于轉向架的封閉式型鋼部件的焊接試件進行疲勞試驗、名義應力和切口應力計算.試驗結果與國際焊接學會推薦數值的差異是由載荷狀況和結構設計引起的.Bertini 等[16]通過純彎、純扭和相位混合加載試驗對一種轉向架用典型焊接接頭開展疲勞強度研究,驗證得到一種修正等效應力,與常用的Mises 等效應力相比具有更低的離散度和更高的斜率,且適用于所有的實驗結果.Ribeiro 等[17]對阿爾法擺式列車的車體和轉向架構架開展動態測試,并將測試結果與建立的有限元模型進行了比對分析.上述文獻大多是基于動態仿真或者臺架試驗進行的研究,并沒有對線路運營條件下動應力損傷及載荷進行關聯研究.

近些年,針對轉向架構架動態載荷問題的研究也有所進展.Ren 等[18]采取試驗測試的方法,得到時速350 km/h 動車組用動車與拖車轉向架軸箱彈簧載荷、定位轉臂座橫向載荷和動態應力,并對載荷與應力特性進行了研究.丁然等[19]采用測力輪對對城際動車組的輪軌力進行線路試驗,得到了輪軌力載荷譜和各工況下輪軌力統計特征.Wang 等[20]采用跟蹤測試的方法,得到了動車轉向架軸箱彈簧垂向載荷和轉臂橫向載荷在一個鏇輪周期內的變化規律,并基于此編制構架橫向、浮沉、扭轉和側滾載荷譜.Zhai 等[21]在無砟軌道運營線路進行某型CRH 動車組測試,得到列車動態特性,進而對350 km/h 速度級動車組振動特征和振動性能展開研究.陳道云等[22]基于軸箱垂向加速度的線路實測,采用擴展因子法得到軸箱全壽命周期的垂向加速度載荷譜.Chen 等[23]采用核密度估計法、擴展因子法和損傷一致性理論對構架標準化載荷譜進行了研究.王斌杰等[24]對地鐵車輛轉向架構架進行實際運營條件下的動應力測試,根據載荷標定的結果得到各載荷譜,并對構架的疲勞損傷特征開展研究.楊廣雪等[25]制作了彈簧載荷測試傳感器,通過線路試驗得到各工況下軸箱載荷特性.Zhu 等[26]研究了高速列車轉向架構架結構準靜態和彈性動態載荷譜的理論問題.Ma 等[27]采用高斯核密度估計法對構架載荷譜的分布進行擬合.鄒驊等[28-29]對城際列車構架載荷狀態展開研究,借助標定試驗結果還原出真實作用載荷,最后對構架載荷與應力特征進行分析.王建斌[30]等基于鏇修周期內加速度測試建立了考慮載荷周期劣化的構架疲勞試驗載荷譜.然而,對于大多數情況下,對只具備基于實際營運工況的動應力大數據測試條件下,動車轉向架構架載荷實驗譜問題研究還很欠缺.

隨著運行速度、服役線路及里程的不斷增加,為進一步提高轉向架的運行安全可靠性,本工作提出一種方法將線路實測動應力數據結合構架在實驗室的標定數據,在損傷一致性原則下進行校準,推導出各力系載荷系數,獲得了完全覆蓋關鍵類型測點疲勞損傷的實驗載荷譜.

1 研究方法

結構載荷譜的研究首先需要對載荷系及載荷應力傳遞關系進行確認,準靜態載荷與動態載荷的之間系統輸入與輸出的關系作了如下假設:

(1)線性假設.假設系統的結構動態特性是線性的.即要求結構的總響應是這一時間段該組內每一激勵單獨作用產生的響應的線性疊加.此假設要求在載荷譜計算過程中,對結構的激振要均勻,結構變形不能過大,避免局部產生非線性影響.

(2)穩定假設.假設結構的動態特性不隨時間發生變化.在載荷譜計算分析過程中,傳遞函數是載荷譜反求計算成功與否的關鍵.如果截取載荷?應力傳遞關系時結構實際響應的狀態與結構本身的動態特性不一致,那么載荷識別的準確性將很難保證.

(3)典型假設.假設在運行線路上所獲得的全部數據均具備代表性.即所測試的數據應包含足夠的信息以描述該構架上的載荷特性,并且應力響應完全是由待識別的載荷所產生.

在上述假設條件下從以下三步進行研究.

步驟一:針對轉向架關鍵點布置應變片,在線實測運用條件的動應力數據,由下式計算各測點的等效應力值

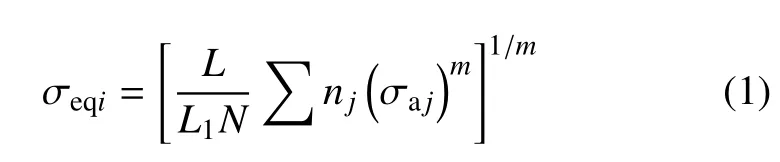
式中各符號說明如下,L為轉向架在規定使用年限內的總運用公里數;L1為實測動應力時的運行公里數;nj為與各級應力水平對應的應力循環次數,即各測點應力譜中各級應力的出現次數;σaj為各級應力水平的幅值(8 級譜有8 個σaj值);m為S-N 曲線方程的指數;N為循環次數,對于焊縫,N取200 萬次.

步驟二:將線路測試的構架放置實驗室內進行標定,建立載荷系并獲得載荷與應力傳遞關系.通過下式確定各個標定載荷在測點處產生的應力響應σij,并挑選載荷響應大的點作為下一步驟計算的基礎

各個載荷系作用下合成響應為

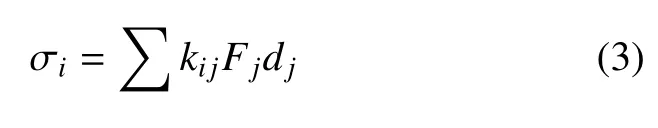
式中,i為測點號,j為各標定載荷序號;Kij代表載荷應力傳遞系數;Fj代表各個標定的單位載荷;dj為載荷系數.

步驟三:根據線路的動應力數據計算各個點等效應力,將該等效應力作為實驗室內等效載荷譜的優化目標,獲得實驗室內臺架試驗的實驗譜.由于線路的損傷采用等效應力的方式,而等效應力經過雨流統計后的計算結果,是不能簡單進行加減的,因此將加載模式簡化,采用恒幅恒頻率加載,這樣,室內疲勞試驗的各個測點的應力值就可以直接與線路的等效應力值進行加減乘除運算.

由此設定優化目標,目標函數為

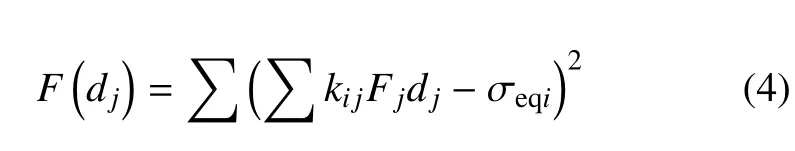
式中kij為載荷傳遞關系系數,Fj為單位載荷,都已知,σeqi為實測等效應力,為已知量.

約束條件的矩陣表達方式為

式中,i為測點號,j為載荷系.

2 線路實測損傷

在轉向架構架主體及承載支吊座的關鍵位置布置測點,見圖1 所示.在京滬京廣和哈大三條高鐵線運行中,實測該轉向架構架上的應力?時間歷程,本研究基于這些主干線路上針對某型號高速動車轉向架進行的長期測試工作,測試車如圖2 所示.圖3 和圖4 中分別示出了橫側梁連接部和制動吊座根部測點的應力的時間歷程波形.

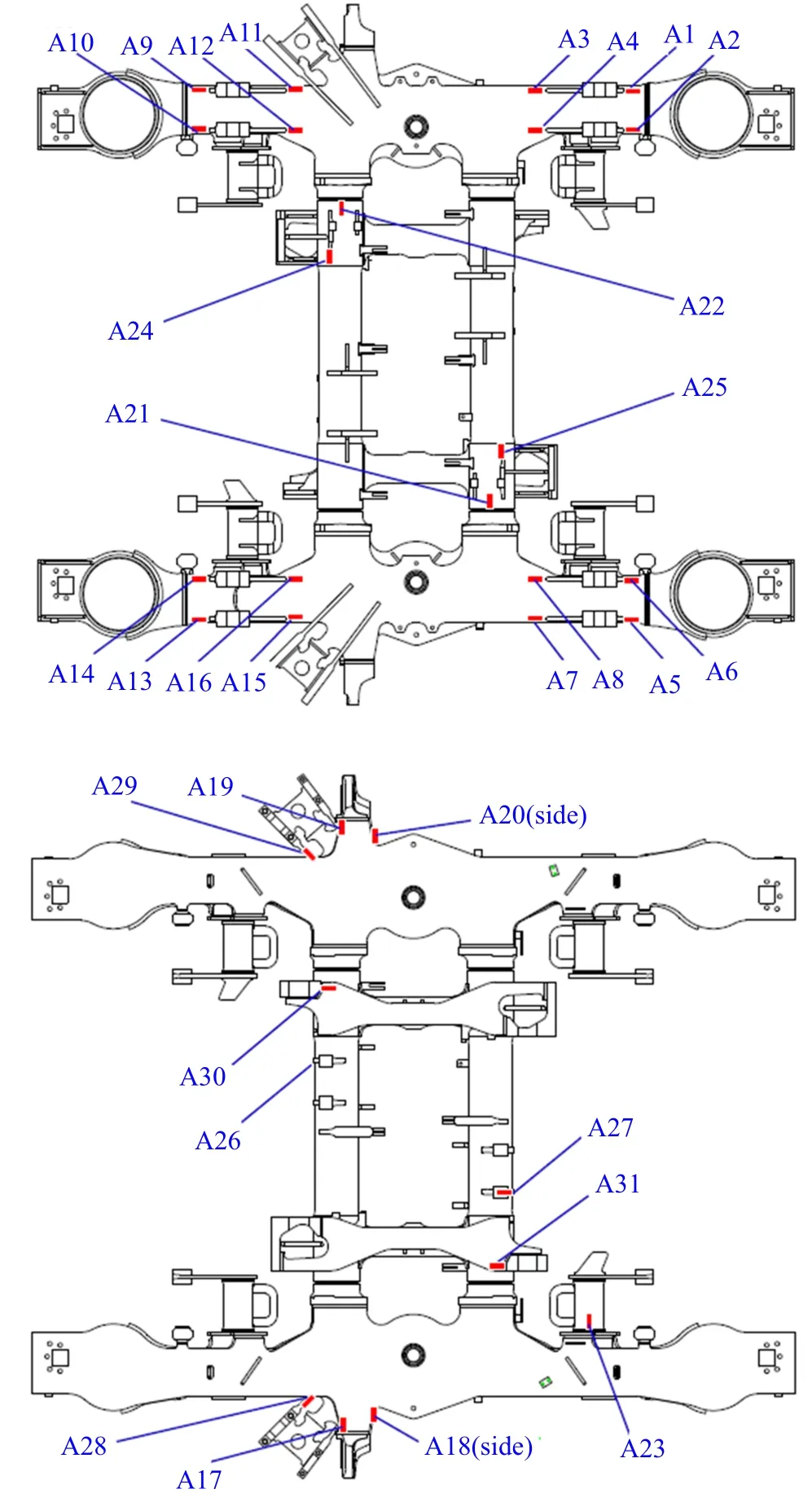
圖1 轉向架構架上測點布置圖Fig.1 Arrangement of measuring points on the bogie frame

圖2 測試車回庫現場Fig.2 Test car back to the depot

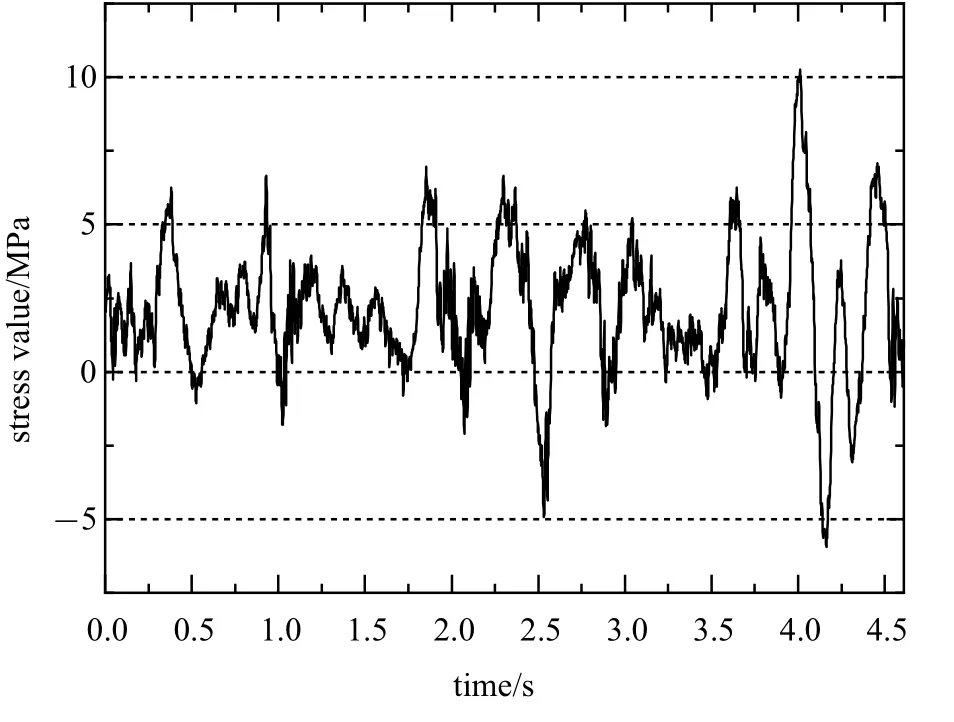
圖3 橫側梁連接部應力的時間歷程波形Fig.3 Stress history waveform of the connection part of the lateral beam

確定12 類部位,布置建立試驗載荷譜的動應力測點.選取的原則是基于構架應力仿真計算響應大小、測點焊接接頭形式、構架受力特點等共性進行分類.本研究根據載荷特征分別為轉臂座根部上外部、上內部、下外部和下內部,抗蛇行座上蓋板區域及其側面,橫側梁連接部下部,制動吊座根部,電機橫向減振器內部,牽引拉桿座根部,抗側滾座根部以及電機吊座根部等區域.選取其中4 個典型測點的應力譜,如表1 所示.

根據12 類的測點實測應力譜,由式(1) 可計算得到它們的等效應力值σeq1,σeq2,···,σeq12.每一個測點在不同線路上的時間歷程是不一樣的,但從這幾大干線挑選出來的等效值能夠滿足具有典型線路特征的最大等效應力值,就能覆蓋所有線路可能出現的典型損傷.

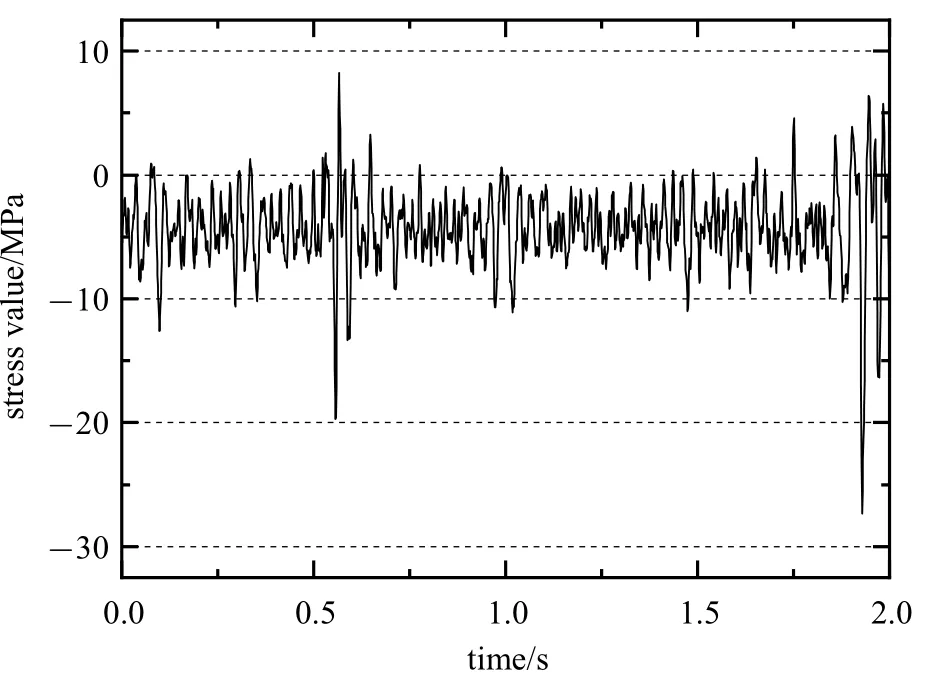
圖4 制動吊座部位應力的時間歷程波形Fig.4 Stress history waveform of brake hanger

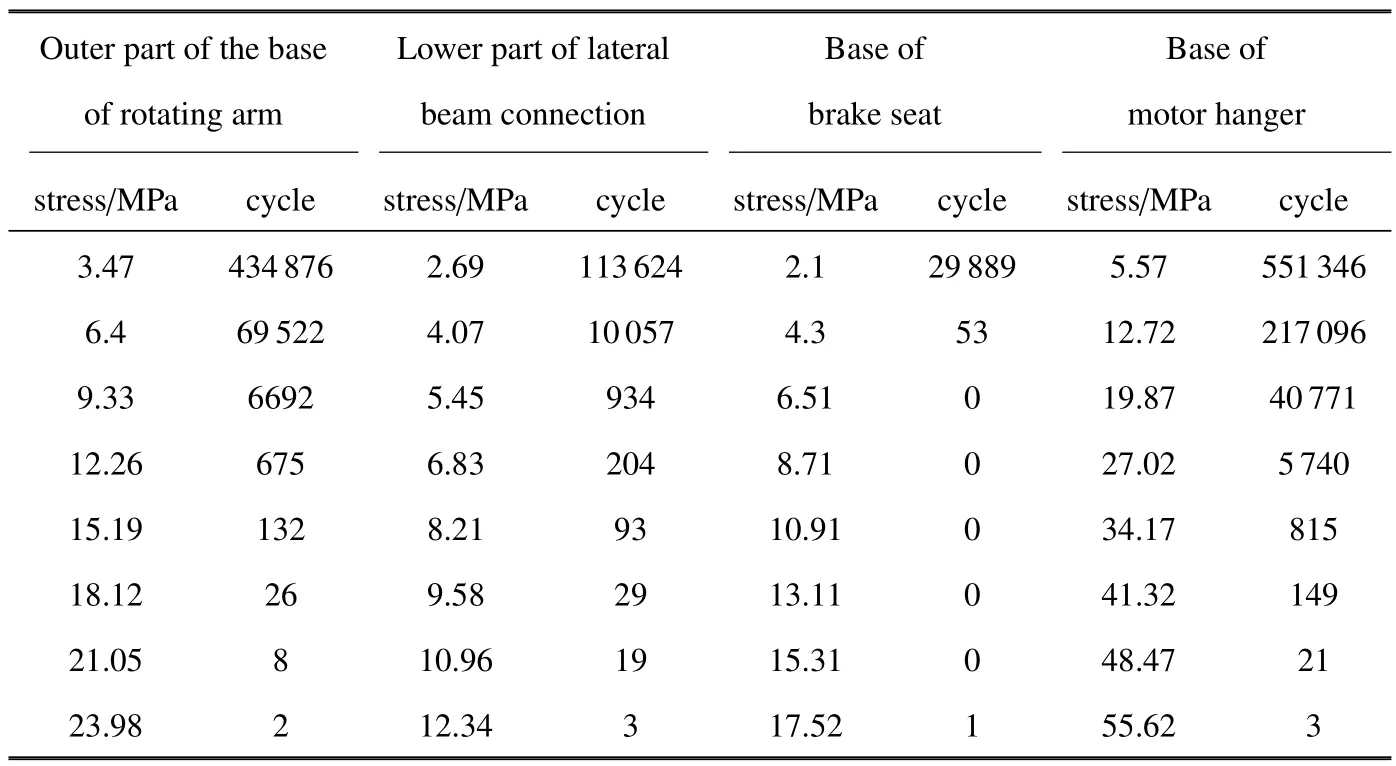
表1 典型測點部位的應力譜Table 1 Stress spectrum of typical measuring points

3 載荷實驗譜編制

轉向架構架上承受的主要載荷如圖5 所示.構架標定現場如圖6,在實驗室進行構架試驗時,如果將一系彈簧載荷視為反力支座加以約束,那么可以將其他載荷系分為:二系垂向載荷、縱向載荷、橫向載荷、抗蛇行載荷、制動載荷、齒輪箱載荷、電機載荷、側滾載荷共八類載荷,每一類載荷都是內在關聯,如同向或反向、或呈一定比例等.由于構架上這些載荷的頻次、幅值不同,這給試驗操作帶來很大困難,甚至難以實施.為此,在編制試驗載荷譜前,對前面所述的假設進行驗證.基于這兩個假設,可將八個載荷系實施分組或幾組同時加載.

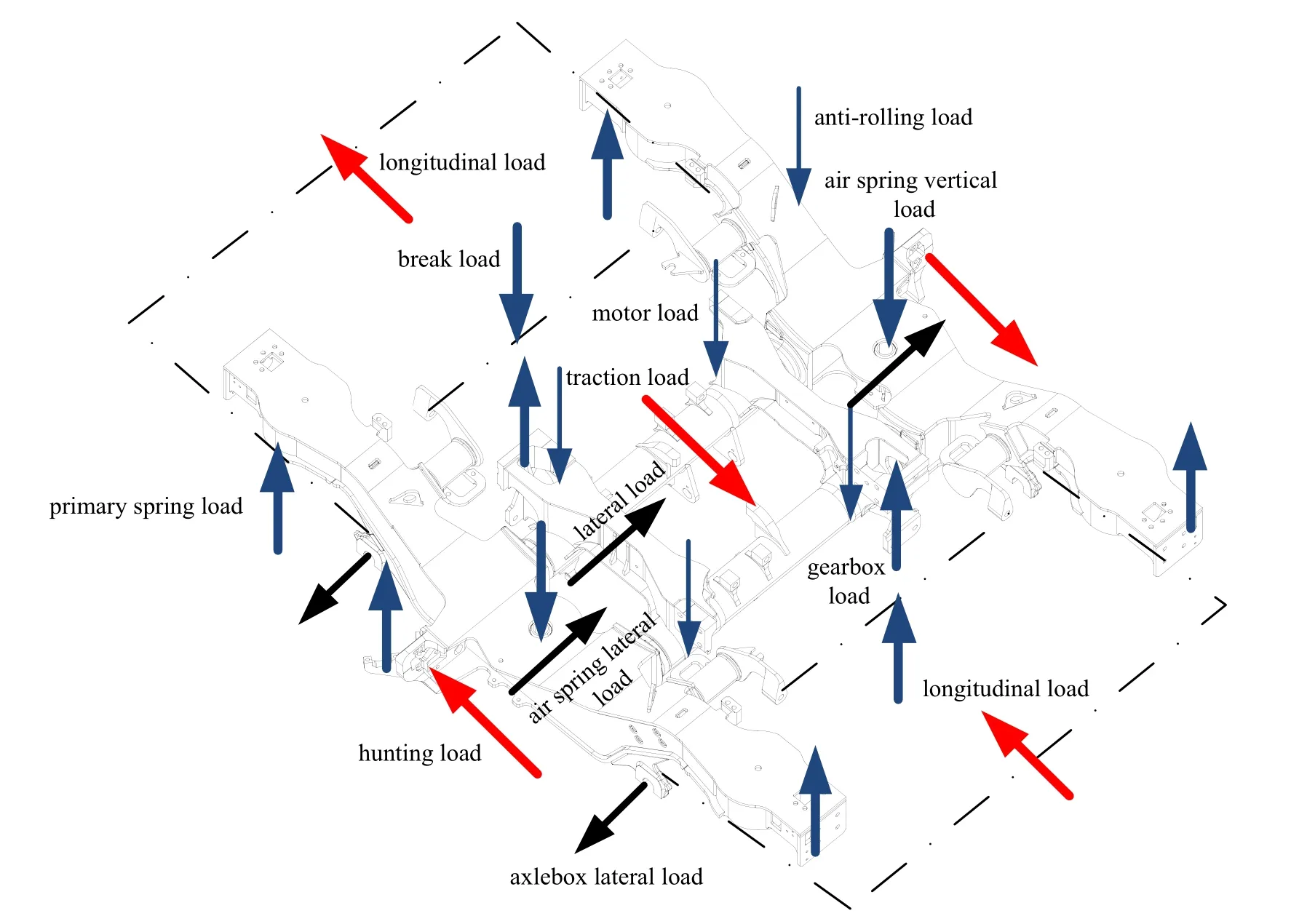
圖5 轉向架構架上的主要載荷系Fig.5 Main load system on the bogie frame

圖6 構架標定現場Fig.6 Bogie frame calibration site

假設1:對于任何一個測點每一個復合工況都可以用單工況線性疊加.表2 中列出了試驗構架在單一加載工況線性疊加與其復合加載在各個測點上的應力測試結果及其誤差值.

對于A1～A31 測點,復合工況即所有單獨載荷力系都依次加載.

由表2 可見,復合工況加載在各測點上產生的應力值比單一加載后線性疊加的應力值大一些,絕大多數測點的誤差值在5%左右,其中最大誤差為7.4%,該假設可以滿足工程需求.

假設2:各測點靜態線性度乘載荷系數與動態幅值的數值基本一致.

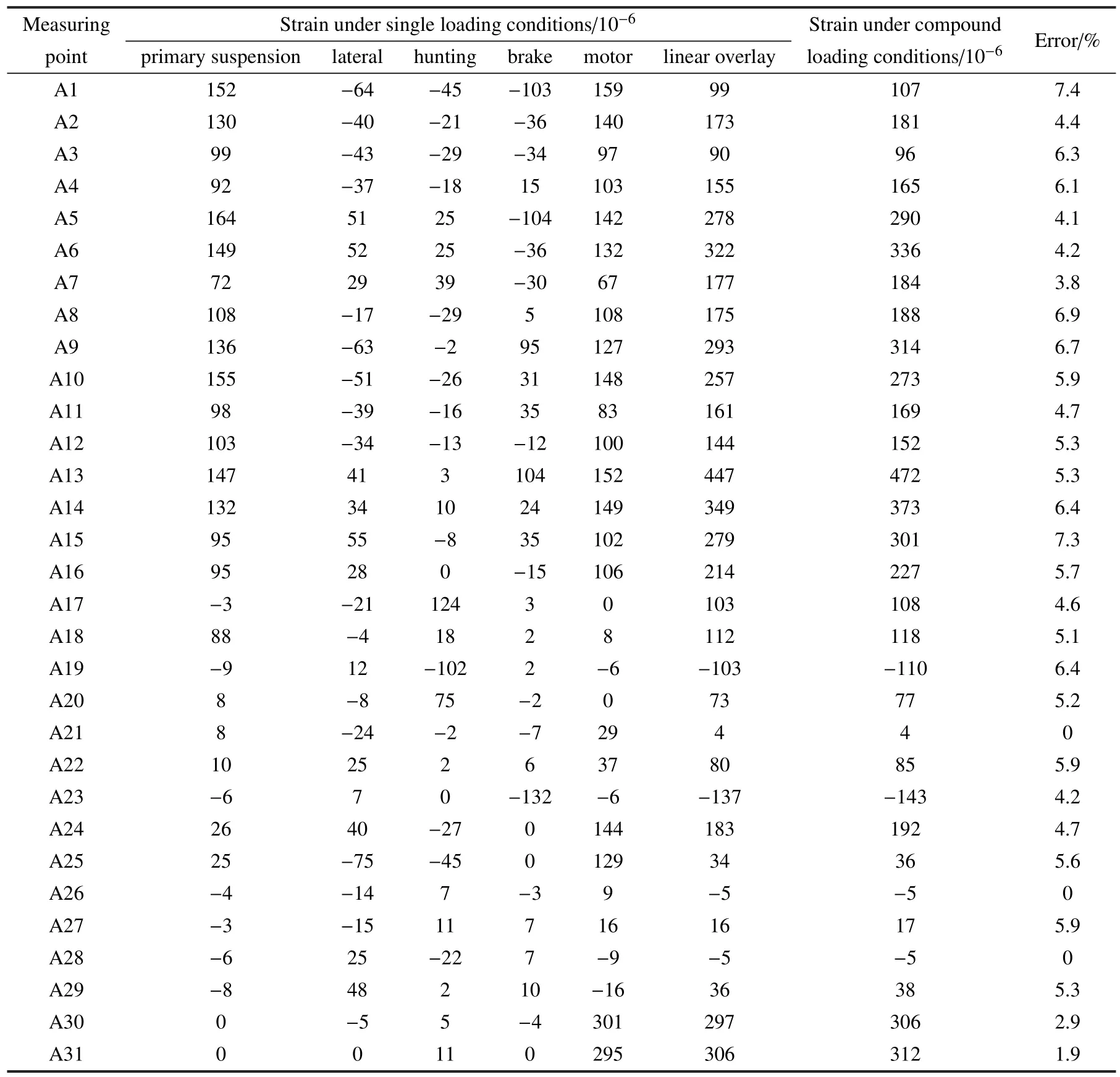
表2 單一加載工況線性疊加與復合加載工況試驗結果Table 2 Test results of linear superposition of single loading conditions and compound loading conditions

由圖7 和圖8 兩圖數據可見,動態恒幅數據與靜態線性數據10%誤差范圍之內,該假設滿足工程要求.

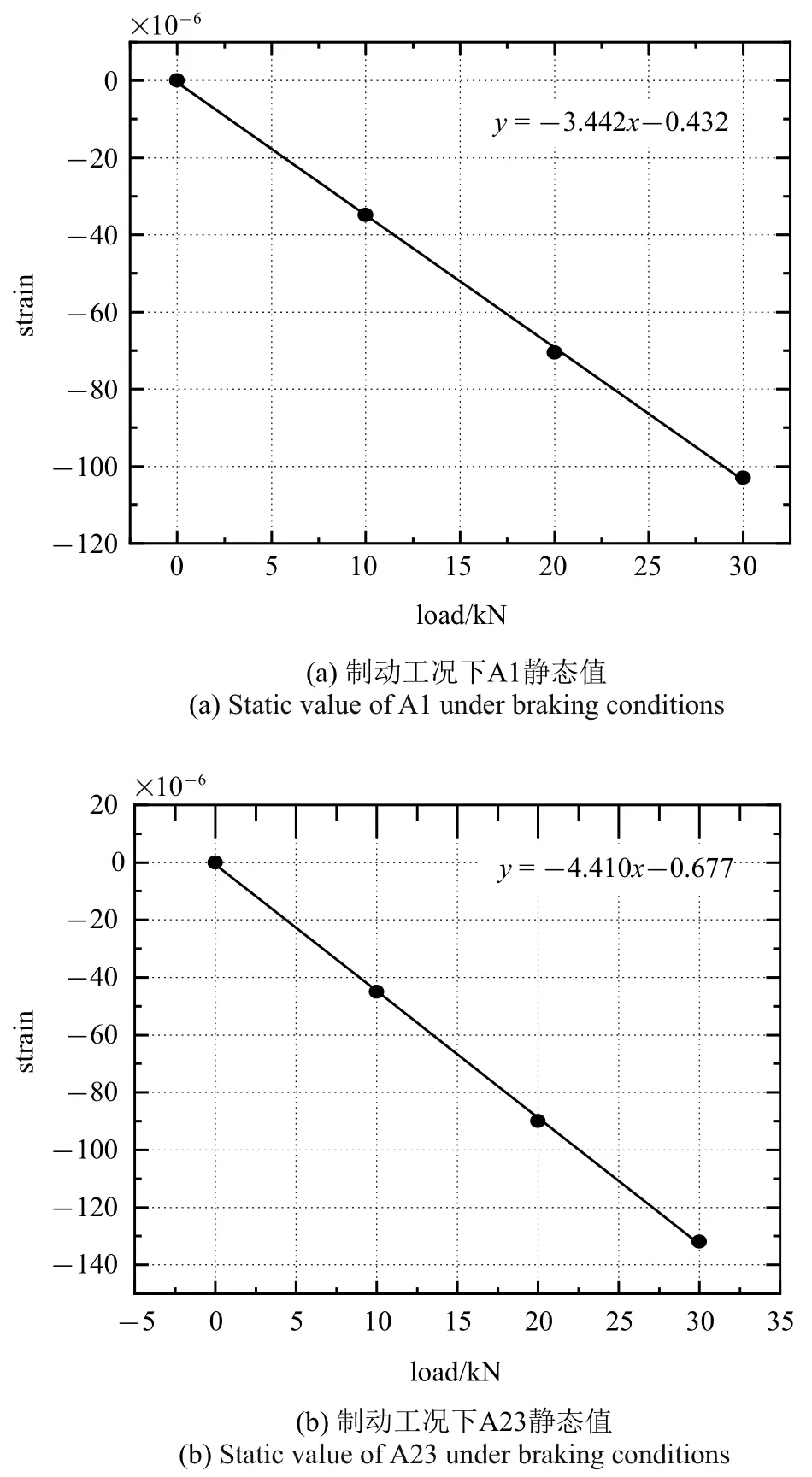
圖7 靜態線性加載Fig.7 Static linear loading

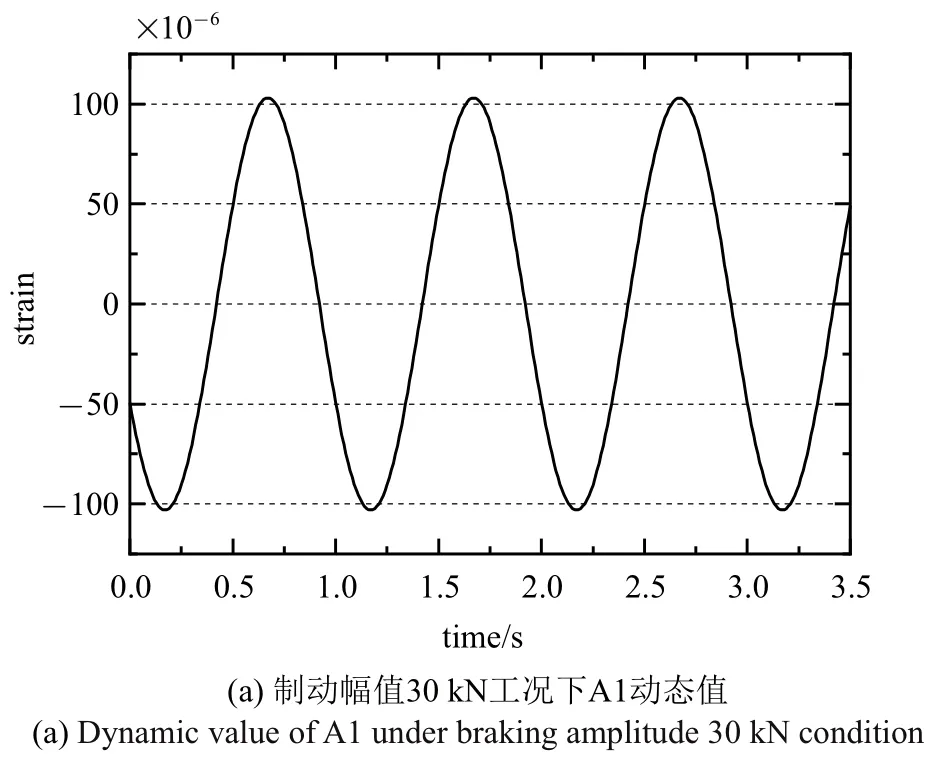
圖8 動態恒幅加載Fig.8 Dynamic constant amplitude loading

4 基于損傷一致性求解載荷系數

對每一個測點進行線性單一加載,得到其載荷?響應系數,如表3 所示.

將所有系數中同類測點的載荷系數最大的點挑出

式中,i代表同類測點,j代表力系.

優化目標函數

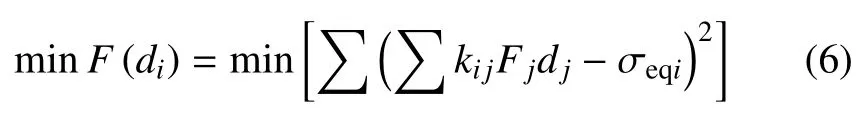
將所有Fj歸一化,均為10 kN,j=0,1,···,8,i=1,2,···,12.

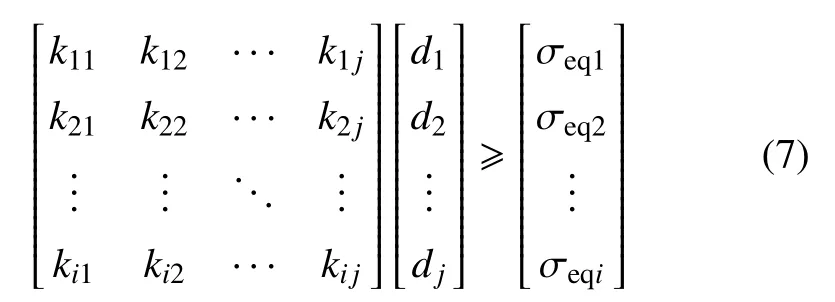
式中,i為測點號,j為載荷系.

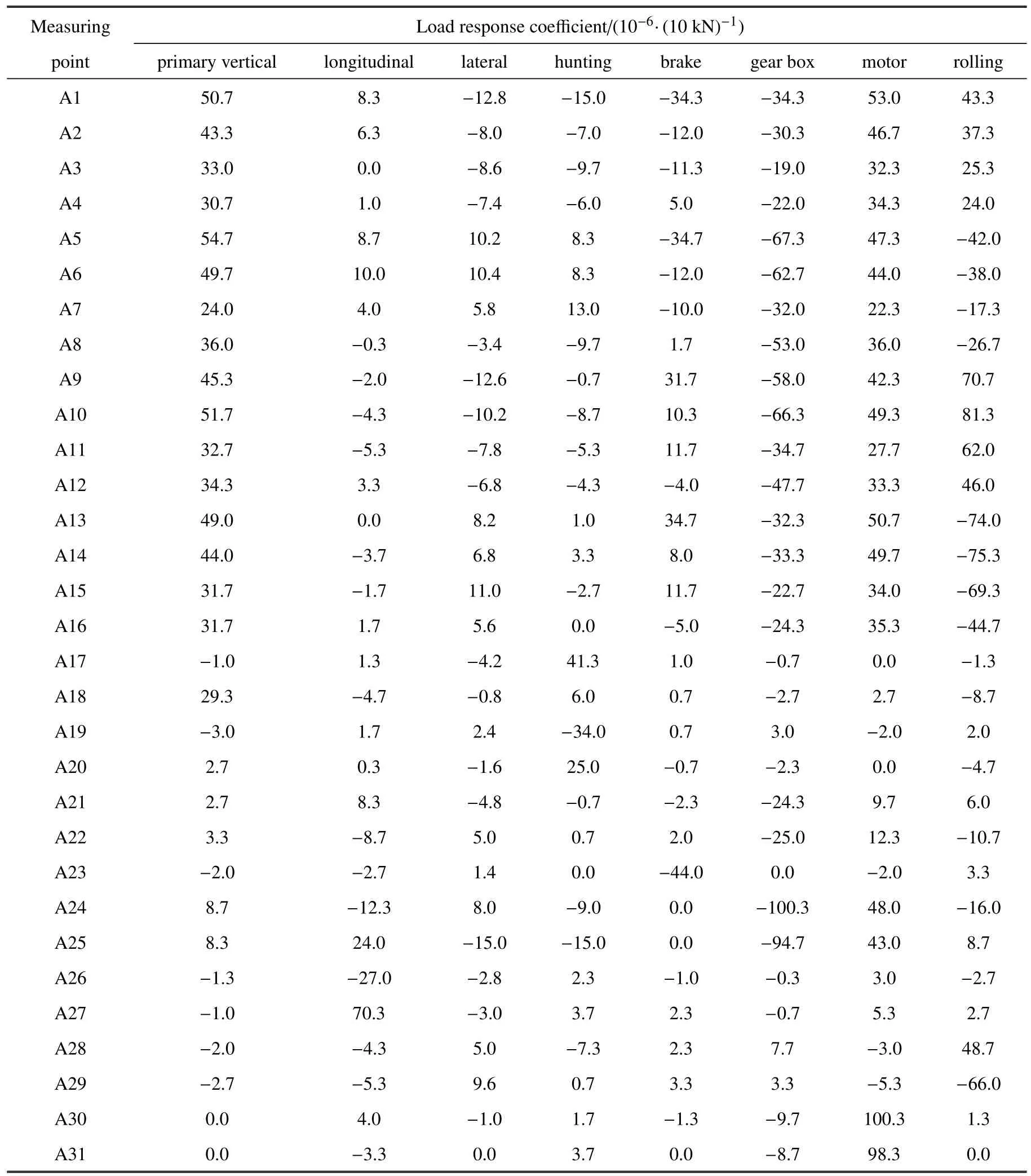
表3 載荷響應系數表Table 3 Load response coefficient

求解可得各個載荷系d1,d2,···,d8系數,乘以10 kN 即可得到每個載荷力系的作用力大小,各個載荷力系相互之間都存在相位差異(正負號),總體為恒幅恒頻加載.

將獲得的載荷值大小導入MTS 多通道疲勞試驗機的控制系統(設備型號FlexTest 200)中,待PID 控制穩定后(如圖9)采集每個測點通道的動態應力值大小.

將所有測點的應力幅值與其線路測試的等效應力值進行比對,得到比值誤差如表4.將所有的比值誤差放入到同一張圖中,如圖10 所示.

圖10 中,所有測點的不同形狀的點代表不同類型測點(12 類),同一類型測點在應力比最大代表該實驗譜下該類測點得到的考核與線路考核的比值(紅色表示).可以看出,在本方法得到的實驗譜中,所有類型測點的最大應力比均大于1,且最大為1.3,所有類型的測點覆蓋了線路測試中的關鍵應力.由于測點眾多,在要求同類型最大點的與線路應力比大于1且最接近1 時,需要調低同類型其他測點誤差,才能做到計算收斂.這也是同類型其他測點有遠小于1的原因.

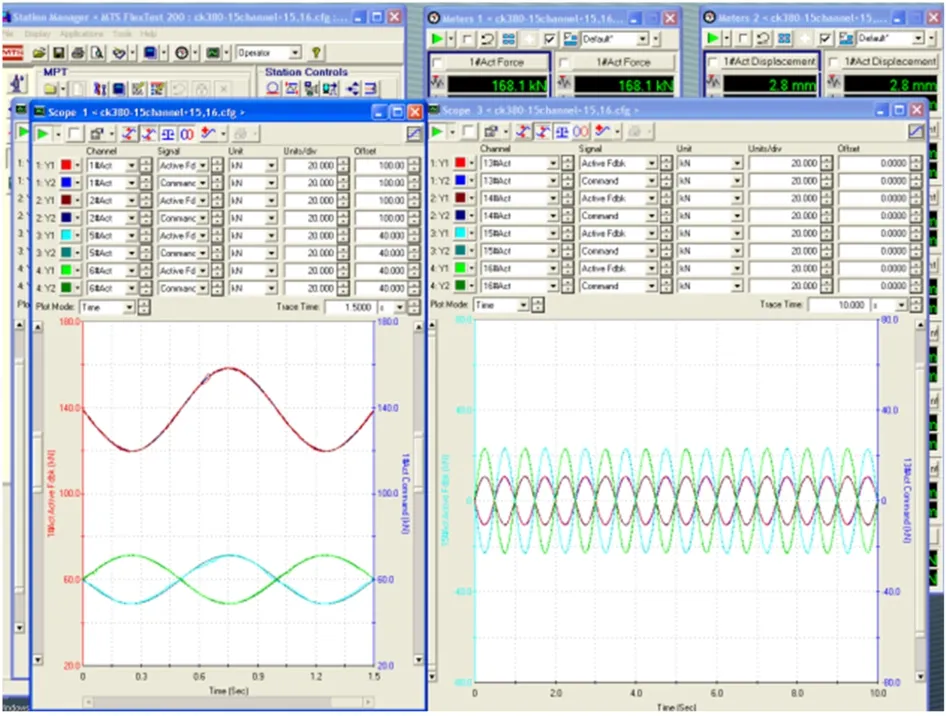
圖9 MTS 載荷控制圖Fig.9 MTS load control

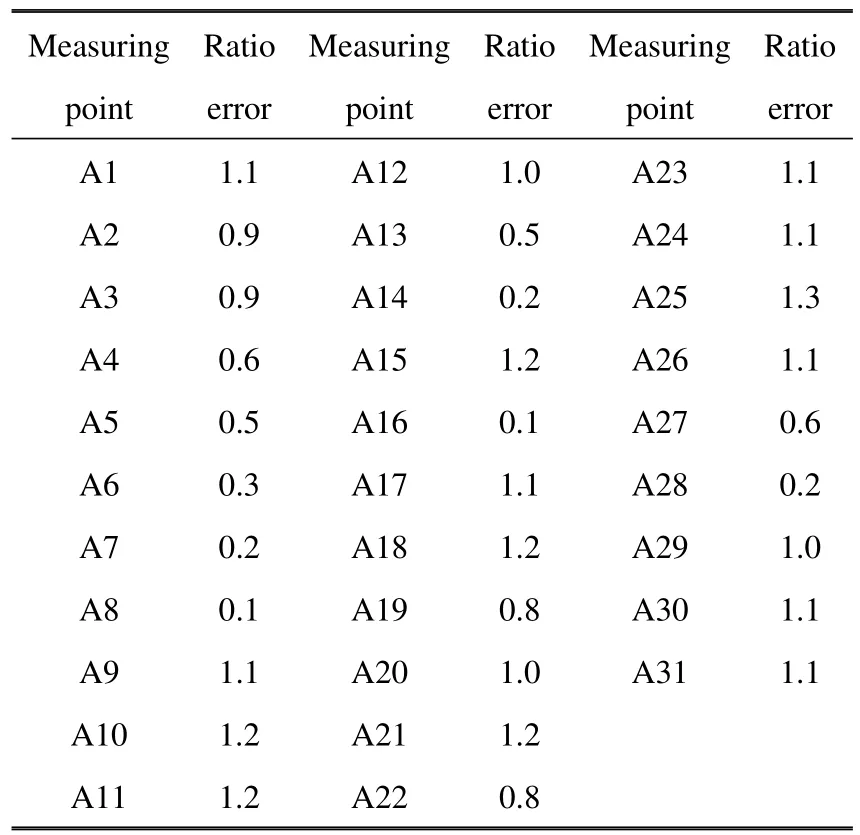
表4 各個測點的比值誤差表Table 4 Ratio error table of each measuring point

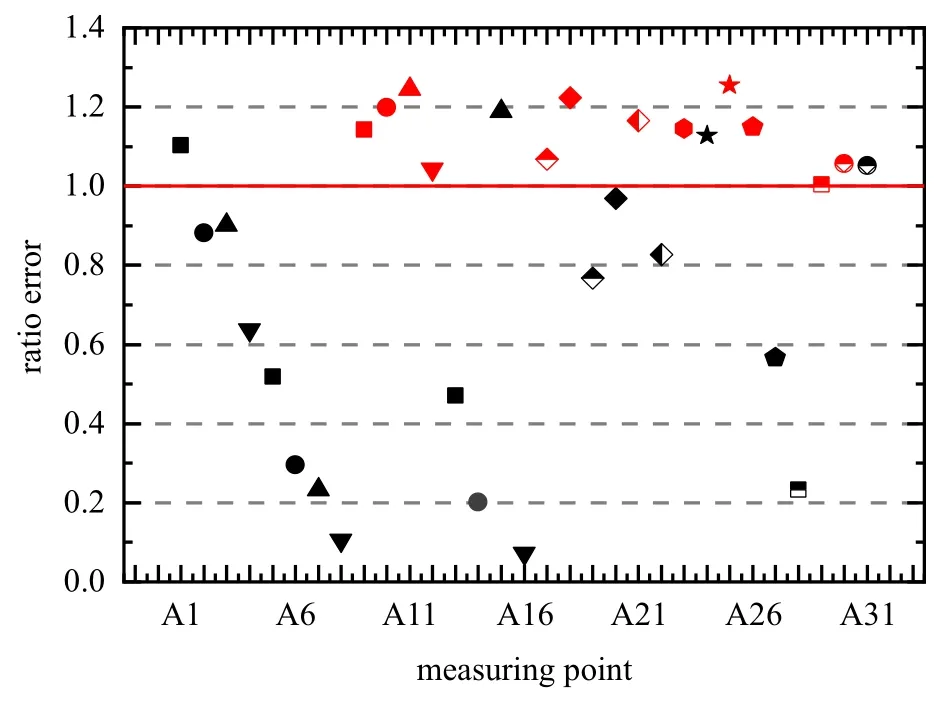
圖10 優化譜比值誤差在歸一化坐標系中的體現Fig.10 Reflection of the optimized spectral ratio error in the normalized coordinate system

采用EN 標準,進行實驗臺架測試,得到的應力值與線路測試應力的比值誤差,放入圖11 中.

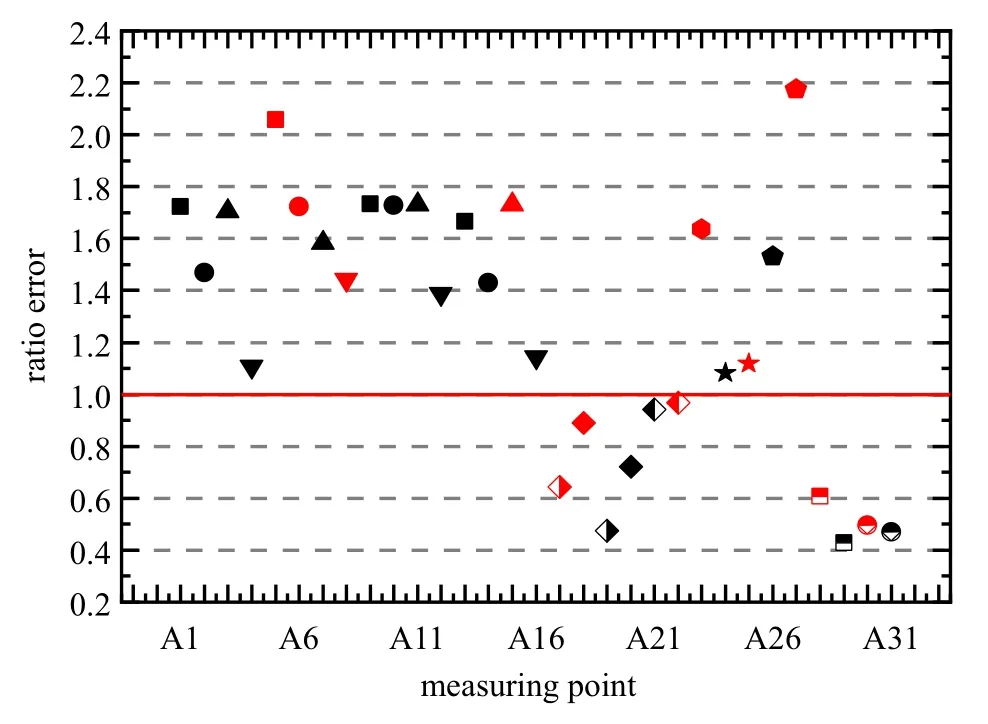
圖11 EN 標準比值誤差在歸一化坐標系中的體現Fig.11 EN standard ratio error in the normalized coordinate system

載荷差異:根據優化后的載荷與EN 標準的載荷見表5.

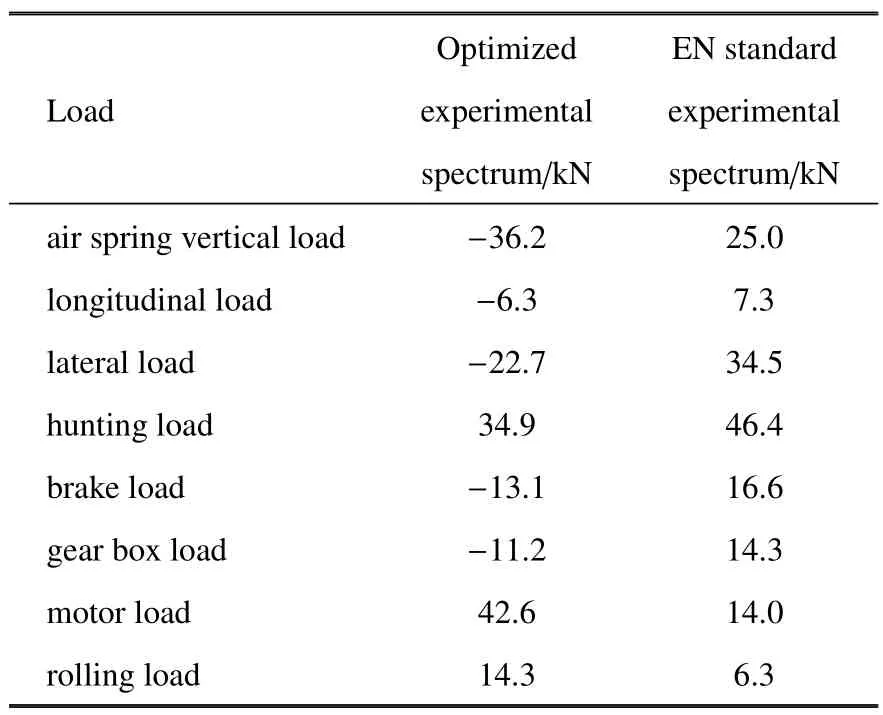
表5 優化實驗譜與EN 標準實驗譜載荷值Table 5 Optimized experimental spectrum and EN standard experimental spectrum load value

從表5 中可以看出,大部分優化后的載荷與EN標準載荷相比稍微減小,但是由于電機吊座附近測點響應較大,而電機載荷對該測點的損傷貢獻大,需要提高電機載荷,這也說明優化后的載荷對于線路條件具有很好的適應性.

從上述圖表也可以看出,EN 標準在建立之初并沒有考慮到中國線路的高速營運條件,其載荷制定雖然考慮了安全性,整體數值較大,但對中國線路上運行的轉向架損傷并沒有較好的覆蓋性.

5 結論

本文從實際運用出發,基于損傷一致性準則與優化算法,針對某動車組轉向架構架實驗譜展開研究,得到結論如下:

(1)在實驗室臺架實驗中,假設條件中線性條件和穩定條件成立,該假設為本研究方案奠定了良好的計算與試驗基礎.

(2)在沒有獲得線路載荷,僅有長期測試構架動應力跟蹤試驗大數據的條件下,可以采用本方法獲得轉向架構架的載荷條件,用于考核構架.當然,如果有載荷測試數據,那么本文的方法會有更準確的載荷條件,覆蓋精度也會更高.

(3)和以前沿用通用標準相比,本研究方法從線路實際損傷出發,設計出一套關鍵類型測點完全覆蓋線路損傷的實驗譜,如果考慮可靠性因素加以整體放大,那么該實驗譜就具有很好的定量效果.

(4)中國鐵路的運行速度和運用工況與歐洲相比具有不同的情況,導致現行國際標準下的載荷譜不能覆蓋到中國動車組轉向架構架的某些關鍵部位.與國際標準相比較,采用本研究方法建立的優化實驗譜不僅能夠覆蓋動車組構架的典型疲勞關鍵部位,而且優化實驗譜下的等效應力與線路實測下的等效應力的偏差也更小.本文的研究內容可作為國際標準的有益補充用于對中國鐵路的研究.