六關節機械臂的軌跡規劃

□ 張秀林

甘肅廣播電視大學 蘭州 730050

1 研究背景

目前,工業機器人的使用已非常普遍。但在實際應用中,機械臂在作業時會面臨許多難題,如機械臂在啟動和停止時手部出現嚴重抖動,機械臂末端到達指定位置不夠精確等[1],如果情況比較嚴重,那么會引起機械臂機構嚴重受損[2]。機械臂的工作性能以工作效率和工作可靠性為衡量標準,所以當務之急是如何提高機械臂的工作效率及工作可靠性。

機械臂在沿軌跡運行過程中,要盡量避免角速度及角加速度突變,即運行軌跡曲線應盡量平滑連續,這樣機械臂的運行就會比較平穩。但是在現實中,有時不能保證完全消除運動突變和抖動,機械臂在運行過程中構件的振動也無法完全避免,只能盡量減小。

為了能夠提高機械臂的工作效率和工作可靠性,對機械臂的運動軌跡進行提前規劃非常有必要。一般做法是,在對機械臂進行運行控制之前,提前規劃好機械臂末端的運行軌跡,并采用仿真技術模擬試驗,由模擬結果來分析機械臂的運行是否平穩,然后將預定軌跡信息輸入控制系統,來控制機械臂的運行[3]。筆者對六關節機械臂進行軌跡規劃。

2 軌跡規劃概述

機械臂軌跡規劃指在機械臂運動學和動力學的基礎上,討論在關節空間或笛卡兒空間中生產機械臂運動軌跡的方法,描述機械臂在多維空間中的運動路線,是運動學逆解的實際應用。在知道末端位姿的前提下,通過運動學逆解得到各個關節在相應時刻的轉動量或平移量,合理規劃出角位移曲線、角速度曲線、角加速度曲線,從而有效控制機械臂在運動過程中的沖擊和振動,使機械臂的工作壽命得以延長。

機械臂運行軌跡端點既可以用關節坐標給定,也可以用笛卡兒坐標給定。筆者以六關節機械臂為研究對象,首先分析對比在關節空間和笛卡爾空間中進行機械臂軌跡規劃的優缺點,選擇合適的軌跡規劃坐標空間;然后通過查閱大量文獻資料總結分析多種軌跡規劃插值函數,選定B樣條插值計算進行六關節機械臂的軌跡規劃;最后將得到的數據導入ADAMS軟件,進行六關節機械臂軌跡規劃仿真。

3 軌跡規劃坐標空間

在關節空間中進行機械臂的軌跡規劃,將關節變量表示為時間的函數,這一函數的一階、二階導數分別表示機械臂運行的速度和加速度,由此確定各關節的位置、速度、加速度隨時間變化的規律,具有計算快、容易實現等優點,但機械臂末端的運動軌跡不直觀[4]。總體而言,在關節空間進行軌跡規劃有三方面優點:容易實現,直接用運動時間的受控變量規劃運動軌跡,軌跡規劃可接近實時運行進行,缺點是難以確定運動中各桿件的位置。

在笛卡爾空間中進行機械臂的軌跡規劃,應用某種定義的函數來規劃機械臂末端執行器的運動軌跡,將末端執行器位置、速度、加速度表示為時間的函數,其它各關節的位置、速度、加速度由末端執行器導出。通常通過運動學逆解得出關節位移,應用逆雅可比求出關節速度,應用逆雅可比及其導數求出關節加速度。在笛卡爾空間中進行規劃軌跡,末端執行器的運動軌跡清晰、直觀[5]。由于各關節的控制驅動是在關節空間中進行的,因此需要將笛卡爾空間約束轉換至關節空間,而控制器所需要的關節參數通過大量運算得到,由此造成計算量較大。同時,計算結果也很難保證不存在奇異點,如所求軌跡在工作空間之外、關節變量值發生突變等。

由上述分析可見,在關節空間進行軌跡規劃,不需要考慮笛卡爾空間中兩個路徑點之間的軌跡曲線,僅以關節變量表示為時間的函數來描述機械臂的軌跡,計算簡單、容易。由于關節空間與笛卡爾空間并不是連續的對應關系,關節空間內不會產生機構奇異的現象,因此避免了在笛卡爾空間中規劃時所出現的關節失控問題。綜合分析后,筆者選用關節空間進行六關節機械臂的軌跡規劃。

4 軌跡規劃插值函數

在關節空間中進行機械臂軌跡規劃時,需要給定起始點和終止點機械臂末端的位姿,對關節變量進行插值運算。采用逆運動學程序將各關節路徑點轉換為各關節矢量角度值,根據每個關節路徑點擬合出一條光滑曲線,使軌跡從起始點開始,依次通過所有關節路徑點,最后到達終止點,完成軌跡規劃。對于每一段軌跡,各關節運動時間均相同,各關節函數之間相互獨立,這樣保證所有關節同時到達關節路徑點和終止點,從而得到機械臂各關節應有的位置和姿態。

對關節路徑點進行插值時,應滿足一系列約束條件,各個關節的位移、速度、加速度在整個時間間隔內需滿足連續性要求,其極值必須在各個關節變量允許范圍之內。在約束條件下,可以選取不同類型的關節插值函數,生成不同的軌跡。

假設關節變量的時間函數采用多項式序列給定,某關節點軌跡應用P個多項式,要滿足初始和終止條件,保證變量在多項式銜接處的連續性,就需要確定3(P+1)個參數。這種規劃稱為兩點式軌跡規劃。基本的兩點式軌跡規劃方法有三次多項式規劃[6]、五次多項式規劃[7]、帶拋物線過濾的線性規劃、過中間點的軌跡規劃[8]等。

若額外給定附加的中間條件,如位置,則對于每個中間條件,需要增加一個參數,這種規劃稱為帶中間點的兩點式軌跡規劃。通常,可以給定兩個中間位置,一個靠近起始位置,另一個靠近終止位置。這樣除了可以較好地控制運動外,還能夠保證以適當的方向離開起始點和接近終止點。因此,對于連接初始位置和終止位置的每個關節變量,一個奇次多項式就足夠了,或采用兩段四次多項式軌跡加一段三次多項式軌跡[9]、兩段三次軌跡加一段五次軌跡[10]、五段三次軌跡[11]、B樣條曲線規劃[12]。經過分析各種軌跡規劃方法,進行對比,筆者采用B樣條曲線進行六關節機械臂的軌跡規劃。

5 關節空間B樣條曲線軌跡規劃

B樣條函數定義式為:

(1)

式中:u為第i段內的增量參數;Bi,k(u)為第i段k次B樣條基函數,k>1,i=1,2,…,k-1。

設機械臂在關節空間中有型值點P1、P2、…、Pm,由連續條件及邊界條件可以求出m+2個控制點V0、V1、V2、…、Vm+1,每相鄰兩型值點之間用B樣條曲線連接,整個軌跡由m-1段B樣條曲線拼接而成。第i段B樣條曲線連接Pi與Pi+1,第i段B樣條曲線由Vi-1、Vi、Vi+1、Vi+2四個控制點控制,且控制點的坐標為Vi-1(vi-1,qi-1)、Vi(vi,qi)、Vi+1(vi+1,qi+1)、Vi+2(vi+2,qi+2),四階三次均勻B樣條曲線在第i段B樣條曲線u處的矢量表達式θi(u)為:

θi(u)=X0(u)Vi-1+X1(u)Vi+X2(u)Vi+1

+X3(u)Vi+2

(2)

式中:Xi(u)為含有參數u的三次多項式。

根據連續性要求,相鄰兩段B樣條曲線在連接處的矢量θi(u)、θi+1(u)應分別在u=0和u=1處滿足條件:

θi(1)=θi+1(0)

(3)

同理,相鄰兩段B樣條曲線在連接處的速度矢量、加速度矢量、加速度變化率矢量應分別在u=0和u=1處滿足連續性條件。

此外,還必須滿足柯西關系,即坐標變換后不變性條件:

X0(u)+X1(u)+X2(u)+X3(u)=1

(4)

由上述連續性條件和式(4),可以求出Xi(u)多項式為:

(5)

(6)

(7)

(8)

可得第i段B樣條曲線u處矢量θi(u)為:

(9)

參數u取值為0～1之間,就可以得到第i段B樣條曲線。但是,要對型值點進行軌跡規劃,就必須先根據已知的型值點來求出控制點。P1,P2,…,Pm為關節空間的型值點,滿足以下條件:

θi-1(1)=θi(0)=Pii=1,2,…,m-1

(10)

θi-1(1)=θi(0)=(Vi-1+4Vi+Vi+1)/6

(11)

式(10)、式(11)中有m+2個未知數,但實際只有m個方程,因此必須要有另外兩個附加條件,即邊界條件:

V1=V0

(12)

(13)

由式(13)可以確定唯一一組Vi值,由此可以確定三次B樣條曲線。

在第i段B樣條曲線上,任意取一個點,其橫坐標vi(u)為:

(14)

在第i段B樣條曲線上,任意取一個點,其縱坐標qi(u)為:

(15)

B樣條曲線軌跡規劃具有分段處理、計算速度較快、占用計算機內存較少等優點。

6 B樣條插值仿真

以空間圓曲線為預設軌跡,空間圓方程為:

(16)

式中:(x,y,z)為空間圓路徑點坐標;(x0,y0,z0)為空間圓圓心坐標;R為空間圓半徑:θ為空間圓圓心至路徑點連線與X軸正方向的夾角;α為空間圓圓心至路徑點連線在YOZ平面上投影與Y軸正方向的夾角。

在空間圓上均勻取12個路徑點,見表1。

表1 空間圓路徑點坐標

在對六關節機械臂進行ADAMS軟件仿真之前,基于逆運動學,應用MATLAB軟件求解出到達表1中12個路徑點所對應的六關節機械臂的各關節角度[13],見表2。

在ADAMS軟件中進行仿真時,為六關節機械臂各個關節添加驅動函數。

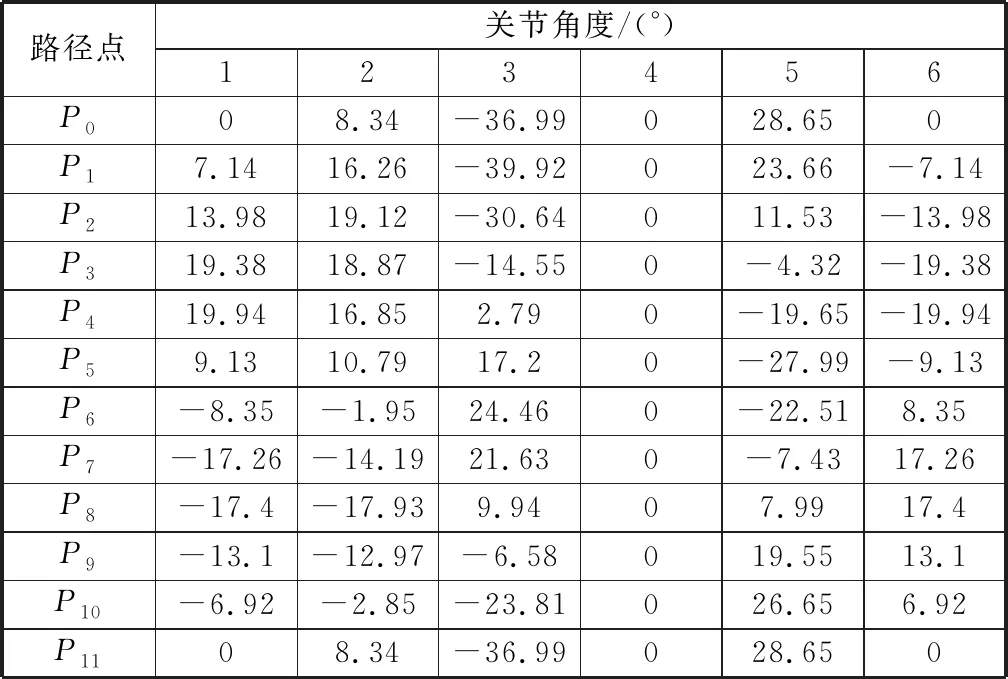
表2 空間圓路徑點對應機械臂關節角度

仿真步數設為50步。在仿真過程中,可以看到六關節機械臂運動過程軌跡比較平穩。各關節的角位移、角速度、角加速度曲線依次如圖1、圖2、圖3所示。

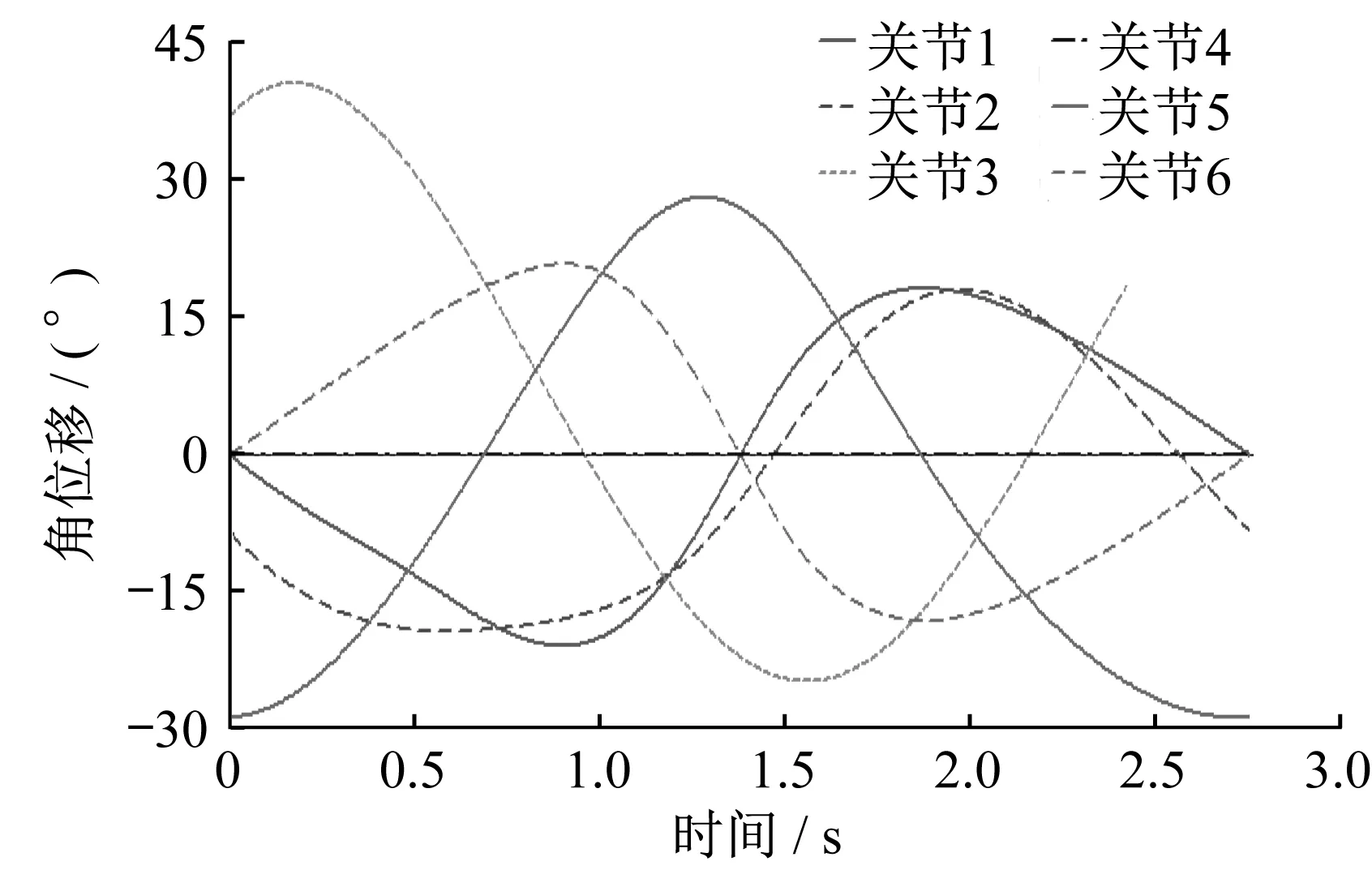
▲圖1 六關節機械臂各關節角位移曲線

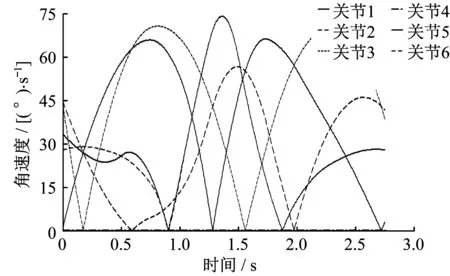
▲圖2 六關節機械臂各關節角速度曲線

由圖1、圖2、圖3可以看出,各關節的角位移曲線平滑,角速度曲線變化平順,但是角加速度曲線有突變點,說明六關節機械臂末端執行器在工作過程中存在振動現象,因此,對六關節機械臂還需要進一步進行優化。

7 結束語

筆者以六關節機械臂為研究對象,在關節空間采用B樣條曲線進行軌跡規劃。在軌跡規則中,對關節空間和笛卡爾空間進行轉換,在笛卡爾坐標系下插補獲得軌跡上的型值點,然后采用逆運動學將這些型值點轉換至關節空間中的各關節角度,再應用B樣條曲線擬合得到各關節的運動軌跡。將得到的數據導入ADAMS軟件進行仿真,得到六關節機械臂各關節角位移、角速度、角加速度變化曲線,結果顯示各關節的角速度變化平緩,角加速度曲線有明顯突變點,因此,對六關節機械臂還需要進一步優化。

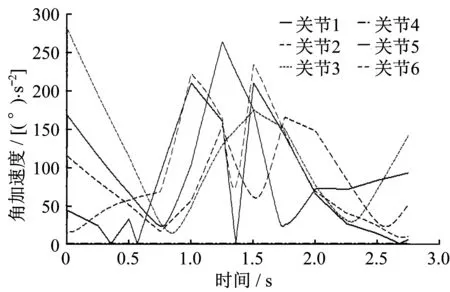
▲圖3 六關節機械臂各關節角加速度曲線