基于多智能體強化學習的空間機械臂軌跡規劃
趙毓,管公順,郭繼峰,于曉強,顏鵬
哈爾濱工業大學 航天學院,哈爾濱 150001
近年來,人類對太空探索和開發活動愈發頻繁,對空間機械臂的能力提出了更高要求[1]。空間飛行器在軌運行過程中,易發生空間碎片近距離碰撞或表面結構脫離等突發情況,可以通過空間機械臂的有效抓捕動作使得飛行器避免主體結構受到損壞[2]。受限于任務場景的動態性和偶發性,傳統空間機械臂軌跡規劃方法難以滿足實時性需求,為了保證能夠高效完成相關動作,亟需開展空間機械臂快速自主在軌捕捉操作的軌跡規劃算法研究[3]。
本文研究的空間自由漂浮機械臂系統軌跡規劃問題與地面機械臂相比,有很大不同:① 空間機器人基座不固定,系統存在非完整約束,無法使用地面機械臂路徑規劃方法求解;② 空間機械臂Jacobi矩陣受載具平臺動力學影響,其動力學奇異比地面機械臂復雜很多;③ 當前通訊條件下很難實現對空間機械臂的地面實時遙操作,因此對其軌跡規劃自主性要求遠高于地面系統。
空間機械臂軌跡規劃目的是,在動力學和運動學約束條件下設計一條以時間為參數的連續曲線,使機械臂末端執行機構在一定時間內達到特定姿態和位置[4]。考慮到空間機械臂在運動過程中會對基座狀態產生擾動,其軌跡規劃問題需要在動量守恒前提下求解,整個系統存在非完整性約束[5]。針對以上特性,傳統方法采用Jacobi矩陣和Lyapunov函數等算法進行系統動力學耦合分析,并以此為基礎進行軌跡規劃。Yoshida等采用廣義Jacobi逆矩陣方式求取可執行軌跡[6]。徐文福采用求解參數方程方法進行軌跡規劃,其中將關節角函數進行參數分解,然后通過牛頓迭代法取得最優解[7]。崔浩和戈新生使用多項式插值結合序列二次規劃方法改進了參數方程求解算法[8]。劉宏等應用控制理論,基于Lyapunov函數對機械臂軌跡進行設計,該方法充分考慮了空間機械臂非完整約束特點[9]。隨著群體智能算法興起,王明等提出了基于群智能粒子群算法的機械臂軌跡規劃方法,并以此實現了最小擾動規劃軌跡[10]。上述基于數值求解和優化的空間機械臂軌跡規劃算法雖然能夠得到較為準確和理想的結果,但始終限制于計算量龐大和局部最優難以跳出的困境,無法應用在實時捕捉系統中。
隨后機械臂運動規劃算法逐漸向全局規劃方向發展,常見機械臂全局軌跡規劃方法包括人工勢場法[11]、隨機采樣法[12]和智能優化方法[13]。早期有學者提出適用于不確定動態環境的基于隨機采樣機械臂運動規劃算法,研究主要圍繞快速擴展隨機樹(Rapidly-exploring Random Trees, RRT)方法開展[14-15]。基于RRT的算法雖然在一定程度上解決了奇點問題和不確定環境問題,但運算效率仍然是其瓶頸。本文采用文獻[16]中改進RRT算法作為對比方法,應用在所研究場景中。
伴隨人工智能技術研究的熱潮[17-18],以強化學習[19-20]和深度學習[21-22]為代表的自學習算法被廣泛應用于機械臂運動規劃工程問題中。基于機器學習算法進行空間機械臂軌跡規劃的優點為其適用性較強,對非完整約束可以進行有效求解,也可以在無模型的條件下進行訓練仿真,甚至可以實現規劃行為的預測和提前分解。2017年OpenAI研究組發表了一種基于多智能體的Actor-Critic研究方法,該方法用于訓練智能體在特定環境中進行協同決策[23]。本文提出的自學習訓練方法靈感即來源于此文,空間機械臂系統可以視為由多個獨立的機械剛體關節桿件組成,其中每個關節桿件都可以看成一個智能體。由此,空間機械臂對運動目標捕捉的規劃問題,可以看作是多個智能體連續動作協同決策問題。
本文針對某型六自由度空間機械臂建立了多關節桿件的標準DH(Denavit-Hartenberg)參數模型。對空間機械臂系統的一般運動方程進行研究,引入多剛體力學耦合特性分析,進一步推導出機械臂與基座的組合體運動學與動力學模型。結合多智能體深度確定性策略梯度學習理論,建立空間機械臂對勻速直線運動目標捕捉的強化學習訓練系統。通過集中訓練與分布式執行方式,對捕捉問題進行智能化自主軌跡規劃。將每個機械臂關節視為一個決策智能體,訓練過程中使用觀察全局的Critic指導訓練,進而實現多智能體的協作行為,提升強化學習穩定性。使用深度強化學習方法進行空間機械臂軌跡規劃的優點在于:避免了復雜系統無法精確建模問題;解決了陷入局部最優解問題;有效降低了實時計算復雜度,提高規劃效率;實現了在線自主軌跡規劃。
本文所述方法是一種即時決策方法,可以進行快速連續決策,不像傳統控制方法需要對控制律進行求解。隨著“數字孿生”等技術的發展,通過計算機仿真模擬即可實現規劃決策神經網絡訓練,離線訓練好的規劃系統移植到實物系統中經過少量在線訓練就能夠達到應用要求。國內很多機構已經實現了地面模擬空間機械臂的實物實驗系統,可以進行地面模擬訓練[24]。基于以上分析,如果未來有應用需求,本文算法可應用于實物驗證和使用環境。
本文所述自學習訓練方法采用Python的TensorFlow工具包進行開發,為了直觀展示所得仿真結果,使用MATLAB的Robotics工具箱進行驗證和繪圖。用于對比分析的改進型RRT算法在MATLAB環境下實現。將兩種方法的仿真結果進行對比分析,可得本文提出的算法得到軌跡規劃時間更短,所得軌跡平滑度更高,對環境參數不確定情況具有較好的魯棒性。
1 問題描述與系統建模
1.1 空間捕捉問題簡化
本文研究對象為在軌運行的自由漂浮小型六自由度機械臂系統,機械臂基座安裝在自由漂浮平臺一端,展開結構如圖1所示。由于空間環境特殊性,僅通過仿真分析驗證算法,并未進行實物實驗。
為了關注軌跡規劃問題本身,對研究環境進行如下假設:
1) 將目標物體理想化為均質小球,球體在機械臂近距離空間內做勻速直線運動,仿真初始時刻一定時間內不會飛出機械臂工作空間。
2) 不考慮末端執行機構對小球的抓捕動作,為機械臂末端位置與球體質心位置重合即為捕捉成功。
3) 將機械臂基座平臺抽象為零控均質剛體,在目標捕捉過程中忽略平臺-機械臂系統整體受到的一切外力和外力矩。
仿真所用機械臂對象的DH參數如表1所示。
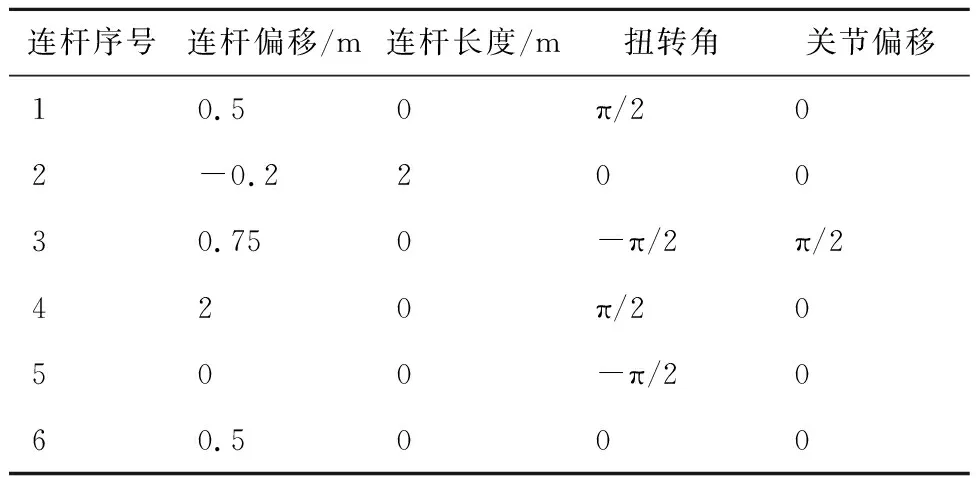
表1 空間機械臂DH參數Table 1 DH parameters of space manipulator
機械臂在非工作狀態下采取收攏姿態,本文研究以此姿態作為空間機械臂初始狀態,如圖2所示。由圖2可以看出,除了關節2有硬性幅度限制外,其余關節均無幅度限制。不失一般性地,設定關節2轉角取值范圍為[0,π],其余關節轉角范圍均為[-π,π]。機械臂動力學參數如表2所示,表中Ix、Iy、Iz分別為轉動慣量在各軸的分量,Tc為關節轉矩。
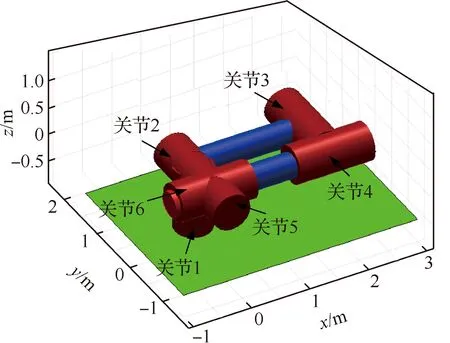
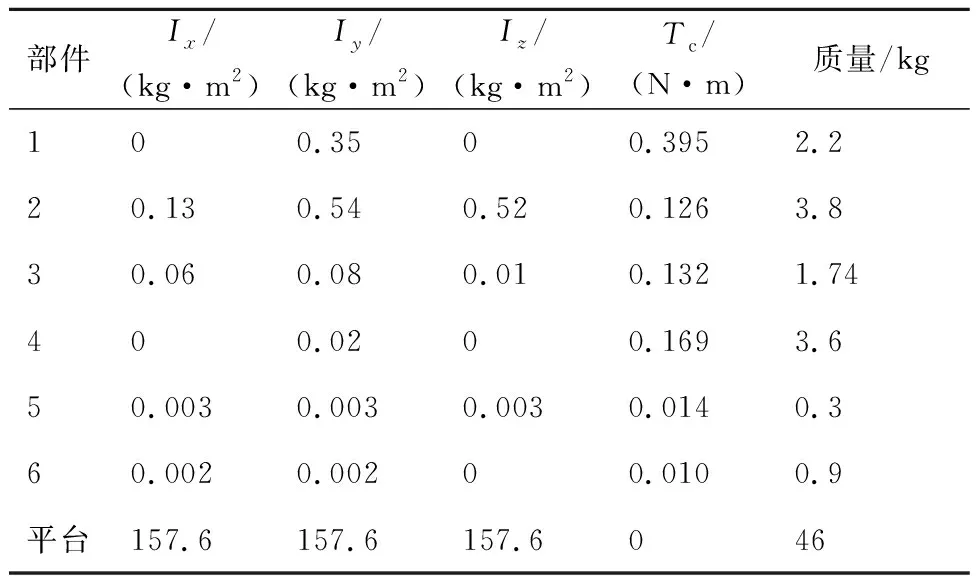
表2 空間機械臂動力學參數Table 2 Dynamic parameters of space manipulator
1.2 空間機械臂運動學模型
對本文研究的空間自由漂浮機械臂系統建立運動學模型,因為機械臂基座固定連接在航天器平臺上,其在捕捉操作期間無控且不受重力影響,所以在機械臂執行動作期間會與平臺產生動力學耦合情況。
由于推導過程較為基礎,在此僅給出重要環節公式,具體的推導過程可參考文獻[25]。針對文中機械臂,根據一般力學原理可得機械臂末端在慣性坐標系下的位置矢量re、速度矢量ve和角速度矢量ωe,具體表達式為
(1)
式中:r0為空間飛行器質心在慣性系中的位置矢量;b0為關節1相對于平臺質心的位置矢量;ai為桿件i相對于關節i的位置矢量;bi為關節i+1相對于桿件i的位置矢量;v0、ω0分別為平臺在慣性系中的速度矢量和角速度矢量;ki為關節i旋轉單位矢量;ri為連桿i的位置矢量;qi為關節i的旋轉角度;“·”表示求導。由于本文研究的機械臂末端關節有位置偏移,所以不能將關節質心作為末端位置進行捕捉結果判斷。
對自由漂浮機械臂應用動量守恒分析,設定初始時刻線動量和角動量均為0,則得到以下多剛體系統約束:
(2)
式中:m0為平臺質量;mLi和mJi分別為連桿i和關節i的質量;pi為關節i的位置矢量;I0、ILi、IJi分別為平臺、連桿i和關節i的轉動慣量矩陣;ωLi、ωJi分別為連桿i和關節i的角速度矢量。
本文為小型機械臂系統,關節質量較輕,在學習訓練過程中可以將同一序號的關節和連桿視為整體,進而降低計算復雜度。由此得到自由漂浮機器人的動量守恒方程為
(3)
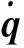
(4)
式中:rL0i表示桿件i指向平臺質心的位置矢量;JTLi、JRLi分別為機械臂切向和徑向轉動慣量。
由式(3)和式(4)進一步推導求解,可得自由漂浮空間機械臂系統的運動學方程為
(5)
式中:Js為平臺Jacobi矩陣;Jm為定基座機械臂Jacobi矩陣,此處不予贅述;re0為末端相對平臺的位置矢量。
1.3 空間機械臂系統動力學模型
本文以拉格朗日法為基礎推導動力學模型。機械臂系統的總動能為各部件動能之和,每個桿件和關節動能可由其質心線速度動能和轉動角速度動能組成,則自由漂浮空間機械臂系統的總動能為
(6)
式中:mi為部件質量;vi為部件慣性系下速度矢量;Ii為部件轉動慣量;ωi為部件角速度矢量。將1.2節中運動學方程代入可得:
(7)
其中:Hφ為定基座機械臂慣性張量矩陣,其表達式為
(8)
則有整個系統的拉格朗日動力學方程為
(9)
式中:cb為平臺本體牽連速度的非線性項,本研究中設定為常值;cm為機械臂牽連速度的非線性項,本研究中設為常值;Fb為基體所受外力及外力矩,前文中已假設為0;τm為機械臂關節力矩。
2 多智能體深度強化學習軌跡規劃
2.1 改進深度確定性策略梯度算法分析
因為載具平臺處于自由漂浮狀態,數學模型無法完全描述系統的非完整性約束。機械臂從收攏狀姿態到捕捉姿態的軌跡規劃可以看作其運動過程中一系列的動作決策行為,每個關節可視為一個決策智能體,最終的軌跡即為所有關節序列決策的集合。為了解決機械臂與環境交互無法精確建模和決策序列集合生成的問題,本文采用深度神經網絡對捕捉軌跡規劃策略進行逼近。
由于機械臂展開抓捕動作為連續動作,其用于評價的Q值函數不易精確設計,因此采用了策略梯度方法解決該問題。策略梯度算法可以通過最大化期望累積獎勵來直接優化策略[26]。考慮到目標移動和環境的隨機性,使用評價器擬合累積獎勵,此評價器被稱為Critic。針對機械臂關節運動取值連續,搜索空間較大的問題,為了縮小隨機策略訓練過程的樣本空間,本文采用了確定性策略梯度方法。確定性策略梯度算法訓練過程中同時學習Q函數和策略,對Q函數的學習是為了實現對環境適度探索。本文算法中執行器(Actor)和評價器(Critic)均采用雙網絡結構,分別稱為決策網絡和估計網絡。在訓練過程中直接對各自估計網絡進行訓練。決策網絡由對應估計網絡每隔一段時間進行優選后保存;評價器的決策網絡同時輸入所有智能體的聯合動作和外部觀測值,對自身某一動作對環境產生的影響進行評價。
下面將給出本文所用多智能體深度強化學習理論公式。深度強化學習過程中,智能體與環境進行交互,期間智能體的決策過程可以用馬爾科夫決策過程(Markov Decision Process, MDP)進行描述。MDP模型是一個五元組(S,A,Ptrans,R,γ),分別對應于狀態空間、動作空間、轉移函數、獎勵函數和折扣因子。對于第i個智能體的執行器Pi和評價器Qi的定義分別為
(10)
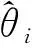
訓練過程評價器策略優化的目標函數為
(11)
式中:E為貝爾曼方程;y代表當前累計獎勵,由迭代而來,為區別于當前動作,累計獎勵相關變量使用“′”表示。然后通過梯度下降法更新網絡參數,對應的梯度計算函數為
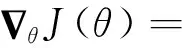
(12)
從式(12)可以看出策略損失的梯度即為策略函數梯度與評價函數梯度的近似數學期望。
為了提高訓練效率,學習過程中設置了經驗池機制,決策網絡定期抽取經驗池信息進行訓練,考慮到經驗池中案例質量分布不均,本文設計了一種優先抽取高質量經驗的方法。設計如下經驗案例抽取優先級Pr(k)公式:

(13)
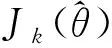
2.2 在線捕捉自學習系統設計
本文的主要工作聚焦于建立自學習系統,通過訓練使漂浮機械臂具備自主捕捉軌跡規劃能力。在2.1節中已經提到,對于每個智能體都將建立4個雙隱層全連接神經網絡:執行器的估計網絡(ActorE)用于策略迭代更新;執行器決策網絡(ActorD)用于經驗池采樣交互,其網絡參數定期從ActorE處更新;評價器估計網絡(CriticE)負責價值函數迭代更新,為當前ActorE的行為更新Q值;評價器決策網絡(CriticD)負責計算全局獎勵,其網絡參數定期從CriticE處更新。訓練系統架構示意圖如圖3所示,其中r1,r2,…,rn為各智能體的回報值。
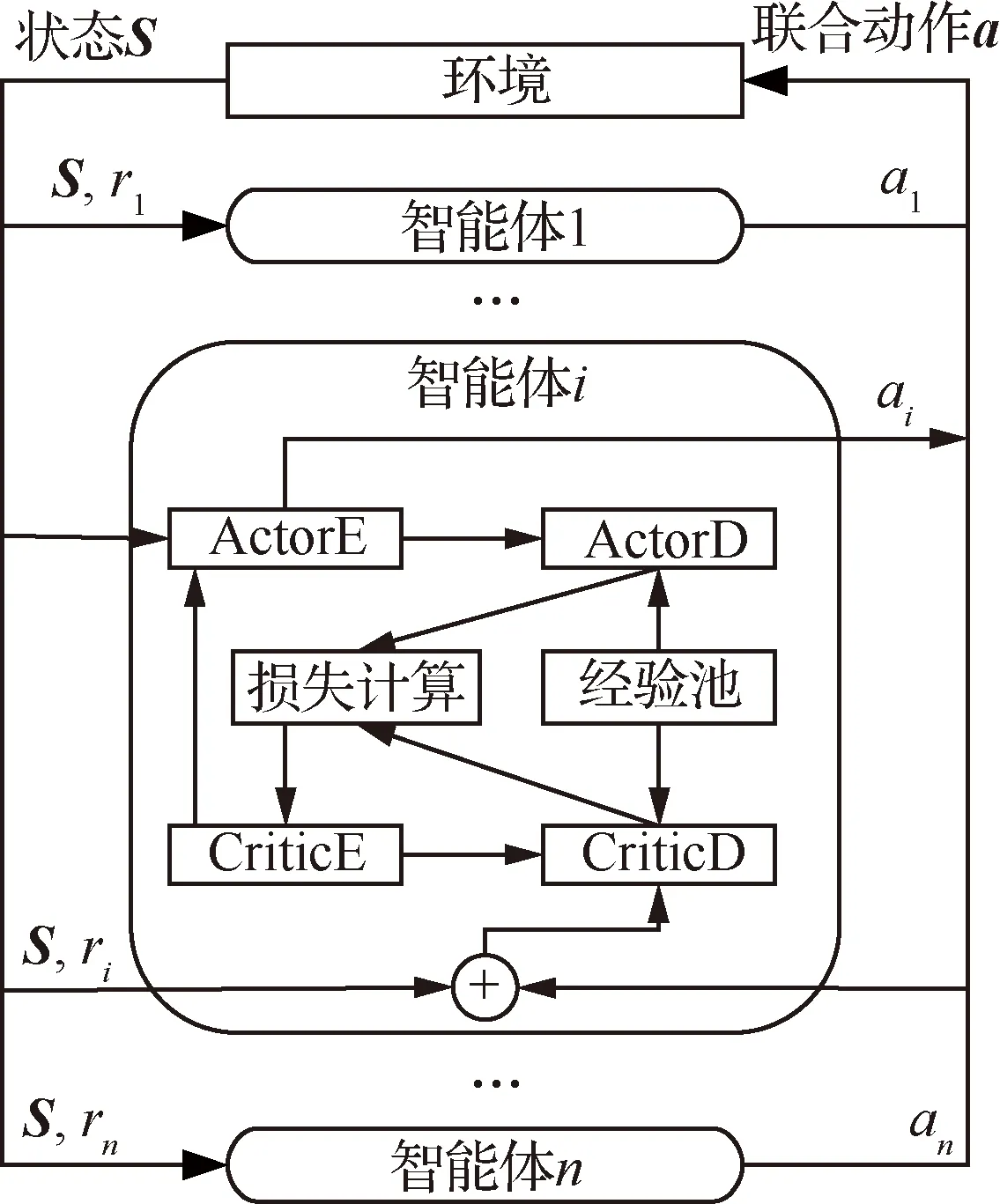
本文采用集中訓練分布執行的方式進行仿真,由于訓練過程中評價器決策網絡的輸入為環境狀態和所有智能體的聯合動作,所以其輸出的評價值函數已經包含了對多智能體協同的指導信息。分布式執行過程中各智能體執行器決策網絡無需溝通,在訓練回合數足夠大的情況下,完全可以通過訓練實現全部協同,而不需要再單獨建立相關機制。但在未來算法改進中可以加入智能體交流機制,使得協同性進一步提升。
為了進一步提高算法執行效率,本文設計了以機械臂末端位置與目標相對距離dT和總操作時間t為參數的獎勵函數:
(14)
式中:ep為動力學參數評價項。由式(14)可以看出,當目標距離越遠則回報值越小,當操作用時越長則回報值越小,如果捕捉成功則獲得固定回報值。對于任意智能體,環境交互得到的獎勵值是相同的。評價器輸入了聯合動作信息,得到評價值不是只受單獨關節動作影響。為了提高算法速度,超過關節運動限制的問題在運動學中處理,不計入獎勵函數。
本文所述多智能體深度強化學習軌跡規劃訓練算法流程如算法1所示。

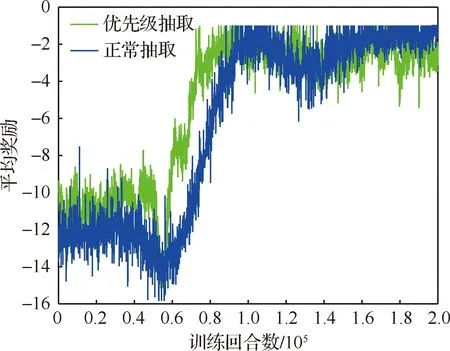
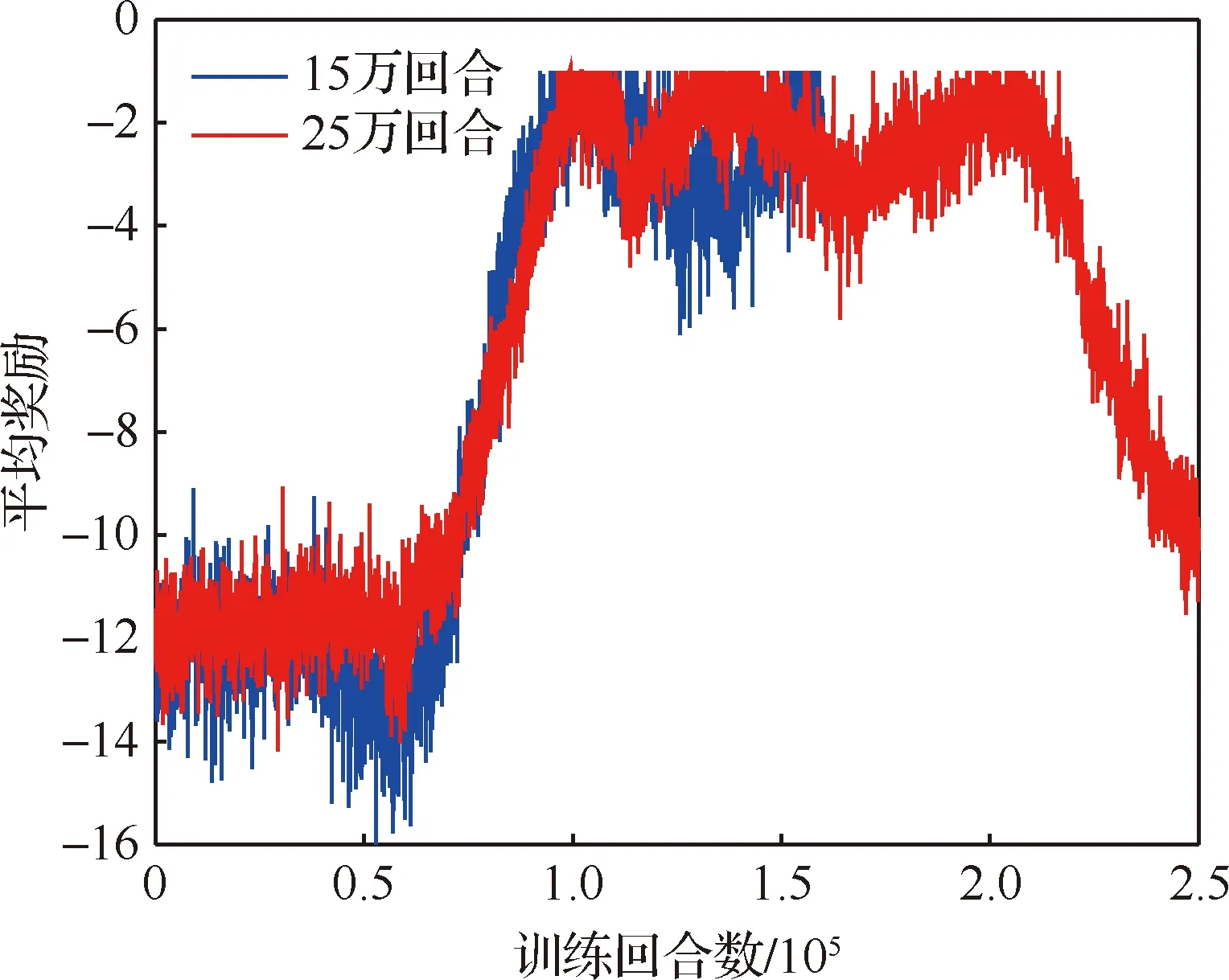
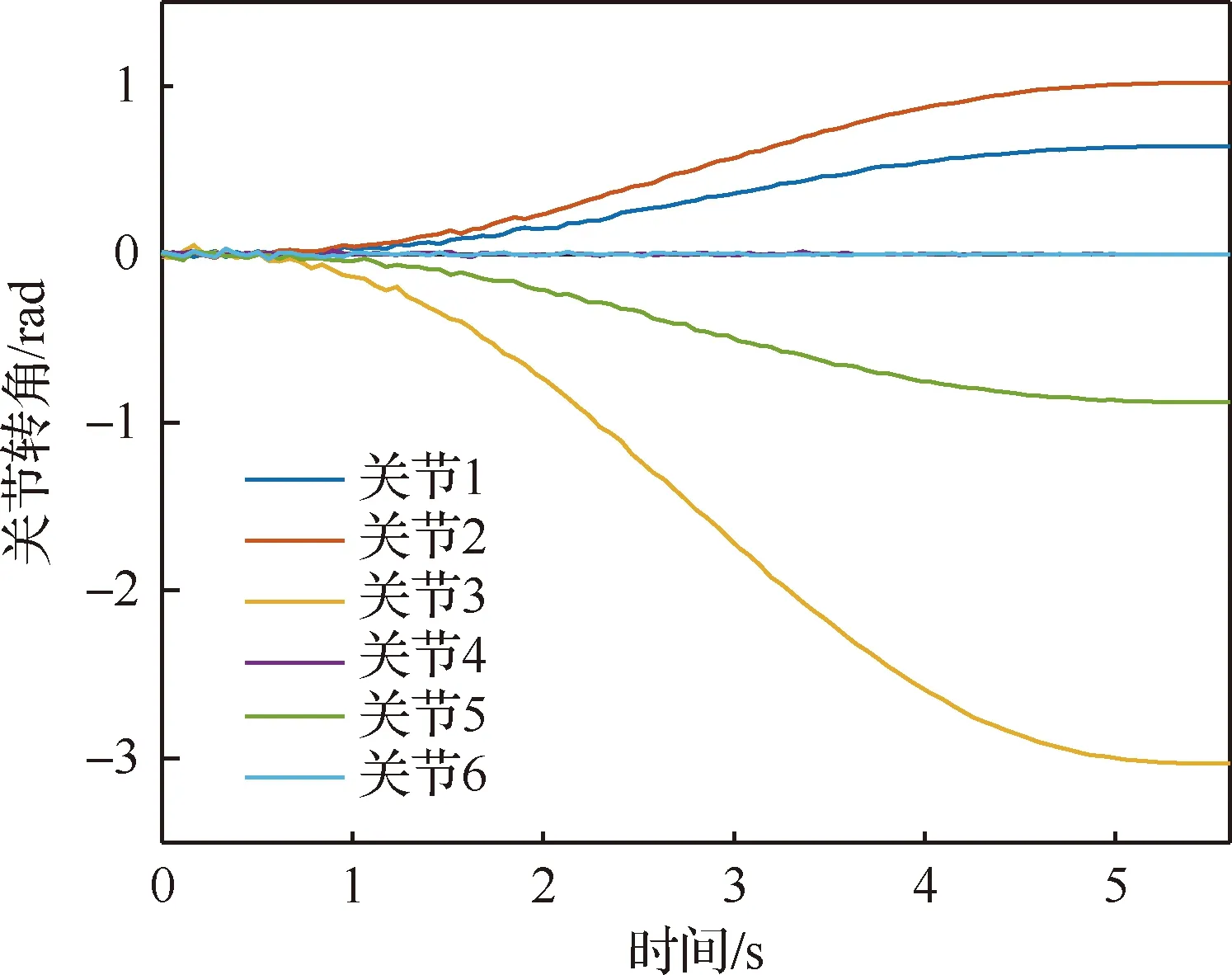
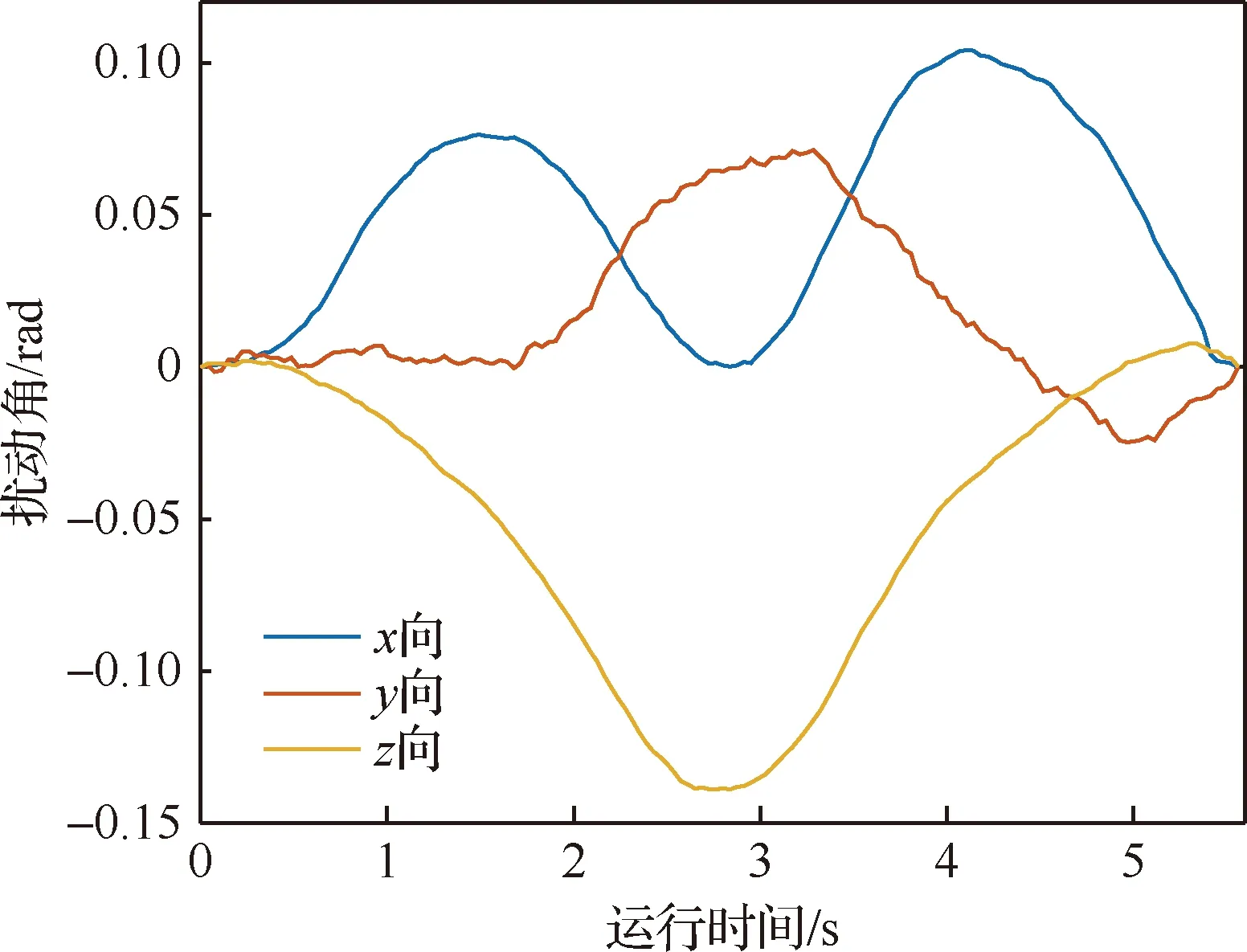
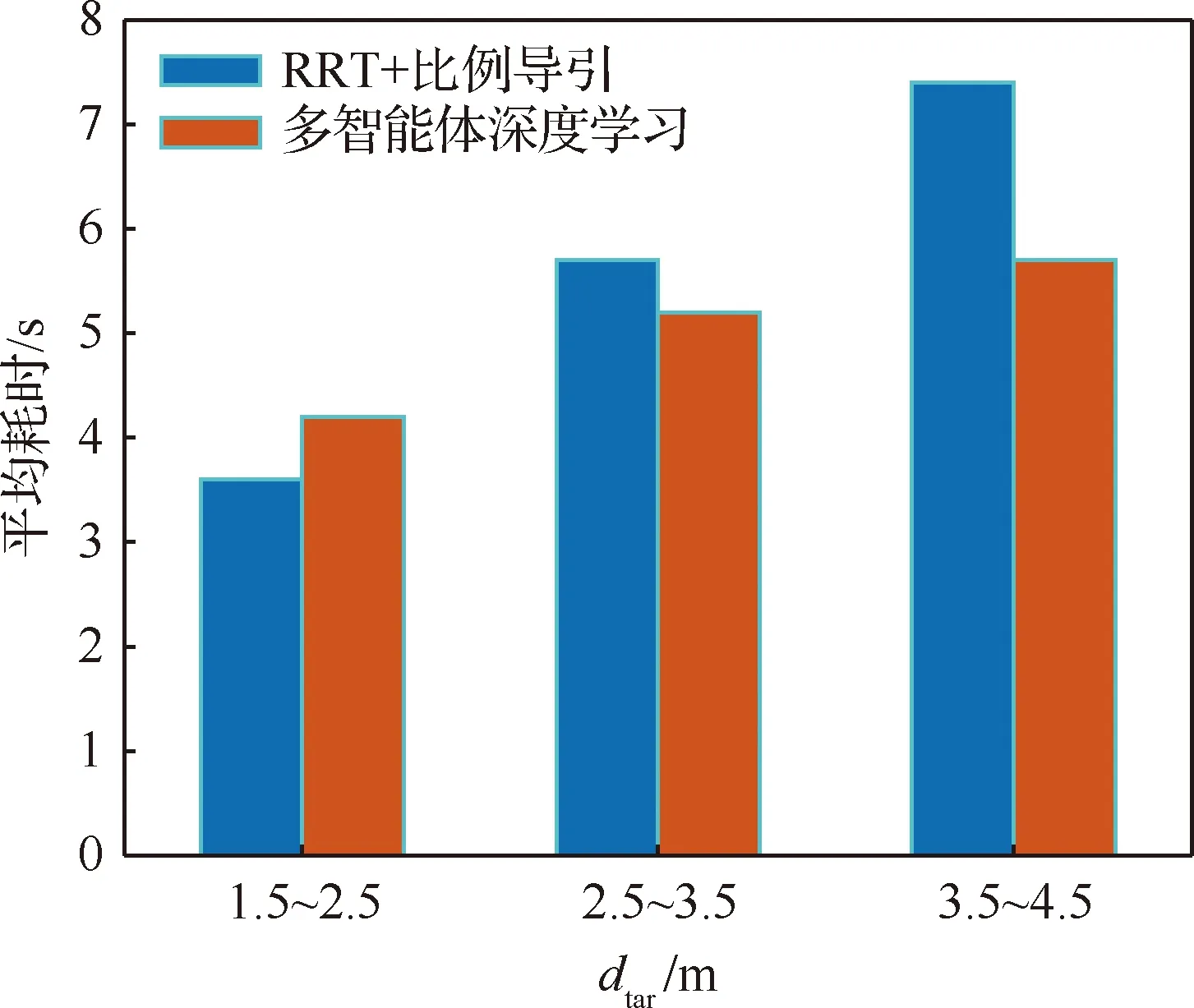
算法1 改進確定性策略梯度算法1.初始化各Agent的ActorE網絡參數θpe、ActorD網絡參數θpd、CriticE網絡參數θQe、CriticD網絡參數θQd2.初始化經驗池ψ,設定各超參數3.for episode = 1 to Max_epi do4. 初始化環境S和各智能體網絡參數5. 設定仿真步長step和最長仿真總時間Tsim6. 隨機生成初始聯合動作集合a=[a1 a2 … an]7. 更新狀態S',得到初始獎勵R0,將案例存儲到經驗池8. do while time i 從以上步驟可以看出,在每個回合中,評價器的決策網絡能夠接收全局信息,進而指導執行器更新網絡,集中訓練的協同性由此體現。規劃算法通過環境、智能體執行器、智能體評價器三者交互來迭代訓練策略網絡。最終形成的智能體執行器決策網絡θpd即為空間漂浮機械臂捕捉行為軌跡規劃器。 操作系統環境為Windows10 x64,使用軟件工具包版本為TensorFlow 2.1.0。硬件信息為Intel i5-9600K、GTX1060、DDR4 16 GB、240 GB SSD。網絡訓練環境是基于Python 3.7修改Open AI開源代碼搭建的。仿真驗證和數據處理均在MATLAB 2018b環境下實現。 在訓練過程中,動力學模型計算后如果機械臂達到平臺邊界,則案例會被直接放棄,重新選擇動作。空間勻速直線運動小球的初始位置隨機選擇在以基座質心為球心,半徑為5 m的半球形包絡內,速度vtar取值不超過0.4 m/s,速度方向矢量與小球位置矢量ptar有如下關系: (15) 式中:dtar為球心與基座間距離;p0為基座位置矢量。 仿真中每個智能體4個神經網絡均采用雙隱層32節點全連接網絡。各神經網絡的輸入輸出信息參見表3,其中關節末端位置由機械臂正運動學解算得出。 表中的聯合動作指所有智能體的動作合集,聯合動作獎勵值即為環境反饋的動作獎勵值,僅是為了區分輸入給對應網絡。從表3中可以看出,執行器和評價器的神經網絡均為高維輸入低維輸出。執行器神經網絡要完成空間坐標向角度映射,所以激活函數采用tanh函數。評價器網絡僅為數值求解,本文采用常見的sigmoid函數作為激活函數。 本文采用文獻[16]中滾動RRT+比例導引算法作為對比算法,該算法將目標捕捉過程分為2個多約束階段,在初始階段使用滾動RRT算法提高搜索能力,在捕捉階段使用比例導引算法提高接近速度。該方法技術細節可參照文獻[16],不予贅述。 表3 各神經網絡輸入輸出參數Table 3 Input and output parameters of neural networks 由于本文中算法沒有完整數據集可以用作對比分析,評價算法優劣的方法主要有2個方面:① 獎勵值曲線變化趨勢,最終獎勵值越高則算法越好,獎勵值曲線收斂速度越快則算法收斂性越好;② 算法所得決策網絡在環境下的表現,動作執行情況越好,則算法性能越好。因為沒有類似自學習規劃算法可以進行比較,所以在后文仿真中,重點對比了決策網絡在實際場景中的表現情況,作為算法主要評價依據。 本文算法可以用平均回報值方差或結果誤差值方差判斷作為終止條件。但設定此條件后,總訓練回合數隨機性過大,無法進行對比展示。所以采用人為確定回合數。仿真實驗首先對經驗案例有無優先抽取機制進行了仿真,經過20萬回合訓練后,得到平均獎勵隨訓練回合數增長曲線如圖4所示。圖中綠色曲線訓練時采用了優先級抽取機制,藍色曲線訓練過程中未使用優先級機制。由圖可知當采取案例優先抽取機制時,平均獎勵曲線收斂速度得到了較大提高。 通過增大仿真回合數檢驗算法收斂趨勢。經過25萬回合的仿真訓練后,得到如圖5所示的平均獎勵曲線,圖中藍色曲線為15萬回合自學習訓練過程平均獎勵值曲線,紅色曲線為25萬回合訓練平均獎勵值曲線。 因為使用了相同的多智能體強化學習算法,可以看到兩個曲線趨勢大體相似。但紅色曲線在21萬回合附近訓練后期,出現了嚴重的過擬合現象。分析該現象產生原因,因為機械臂系統具有完整的約束模型,且訓練過程中不存在外部擾動或噪聲,所以分析認為是空間小球目標的初始位置隨機性波動也被學習系統訓練學習了。 多智能體強化學習系統訓練結束后,執行器的決策網絡訓練成型。設定空間小球的初始位置為ptar=[-1,-0.5,5.8] m,運動目標的初始速度為vtar=[-0.082,-0.037,0.042] m/s,分別使用該規劃決策器和滾動RRT算法對該場景進行機械臂軌跡規劃仿真,得到仿真曲線。圖6為多智能體規劃決策器規劃生成的捕捉過程各關節轉角曲線,圖7為對比算法生成的關節轉角曲線。 對比圖6和圖7可以看出:在同一場景下,本文提出的算法用時約為5.6 s,而對比算法規劃耗時約為7.4 s,可見本文算法規劃效率更高。文中所提出的算法規劃所得曲線較為平滑,而對比算法規劃所得關節轉角曲線相對較粗糙。相比之下,本文算法魯棒性更強。 2種算法在規劃前期曲線都存在抖動。本文所述算法前期抖動的原因是無法直接跟蹤移動目標,且機械臂展開初始階段存在多種可能構型,所以產生了曲線抖動現象,隨著捕捉過程的推進,曲線逐漸變得平滑。而對比算法前期抖動較為明顯,因為該算法規劃前期使用RRT方法,該方法具有隨機搜索特性,在初始階段就產生了非必要的探索行為,中期算法交替時又耗費時間進行軌跡誤差補償,這是影響算法效率的因素之一。對比算法規劃后期因為使用比例導引方法,規劃效率明顯提高,且關節角曲線趨于平滑。 圖8為本文算法在該仿真場景中規劃所得軌跡對應的平臺姿態擾動角曲線圖,擾動角曲線并非在決策器規劃過程中決定,而是規劃軌跡生成后由動力學模型解算得到。從圖8中可以看出,機械臂捕捉動作對漂浮平臺的擾動較小,各向擾動角度均不超過10°,由此也可看出本文算法的有效性和可行性。 為了進一步揭示空間目標與機械臂基座距離和捕捉軌跡規劃耗時的關系,分別對2種算法進行了1 000組不同初始狀態的規劃仿真,對仿真結果進行統計分析,在1.5 m≤dtar<2.5 m時本文算法捕捉規劃平均耗時4.2 s,對比算法平均耗時3.6 s;在2.5 m≤dtar<3.5 m時本文算法平均耗時5.2 s,對比算法平均耗時5.7 s;在3.5 m≤dtar<4.5 m時本文算法平均耗時5.7 s,對比算法平均耗時7.4 s。于是得到如圖9所示柱狀圖。從圖中可以看出,在目標距離較近時本文算法規劃軌跡較慢,此時RRT+比例導引方法規劃效率更高。隨著距離增加,本文方法規劃效率有所提高。分析其中原因,RRT的隨機搜索方法在短距離規劃中具有一定優勢,其在長距離規劃中必然會消耗更多時間來探索執行空間,所以長距離規劃中效率不如本文算法。 對上述1 000次仿真中2種算法耗時情況進行統計,本文所述算法得到平均捕捉完成耗時為5.4 s,對比算法平均耗時為6.3 s,由此可見本文算法規劃效率更高。 1) 本文在機械臂運動學和動力學分析基礎上,提出了基于多智能體系統的強化學習機械臂軌跡規劃方法。 2) 應用本文算法可以快速對空間捕捉問題進行規劃和處理,平均捕捉動作完成耗時5.4 s,相比前人算法規劃效率更高。 3) 仿真結果表明,本文算法規劃所得軌跡曲線更平滑,相比前人算法魯棒性更強,具有很強的實際工程應用價值。3 仿真數據與分析
3.1 仿真條件
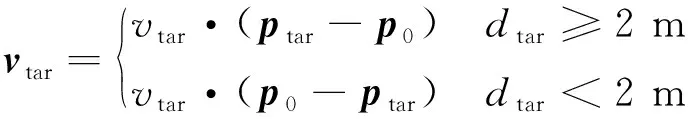
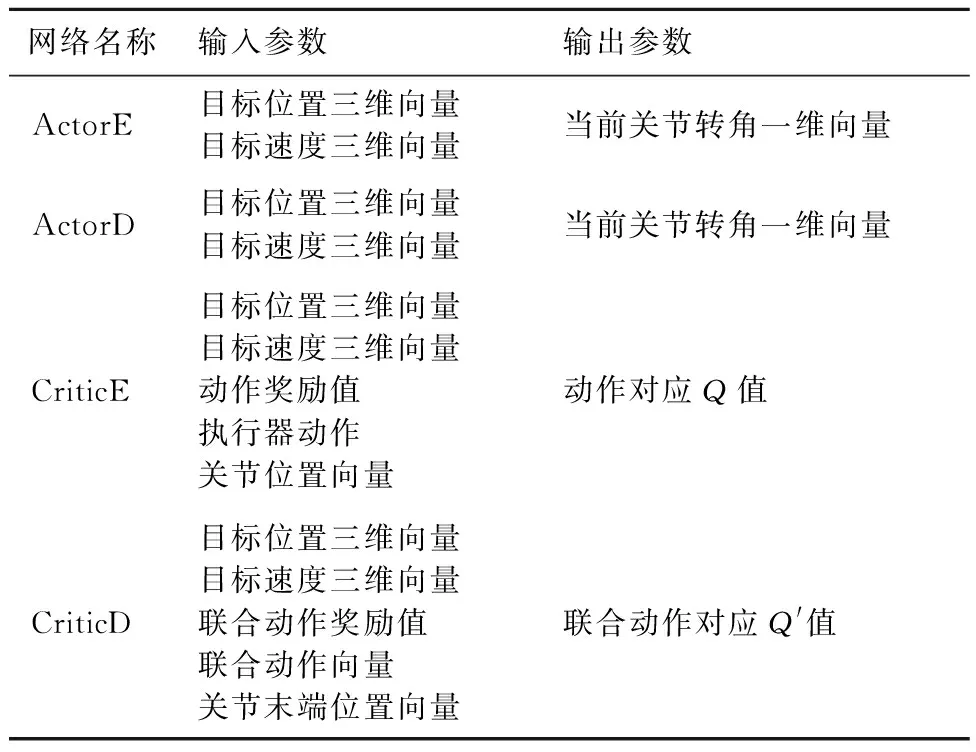
3.2 仿真結果與數據分析
4 結 論

