不同荷載工況下的CRTSⅡ型軌道板混凝土開裂分析

楊艷

不同荷載工況下的CRTSⅡ型軌道板混凝土開裂分析

楊艷

攀枝花學院交通與汽車工程學院, 四川 攀枝花 617000

目前對軌道板開裂計算都局限于一些特殊位置，且忽略了多種荷載工況組合，同時規(guī)范計算軌道板拉壓應力并未細化，不便于實際應用。為了更為全面地反映處于多種荷載工況組合下的單塊軌道板各個位置處裂紋情況，本文借助通用軟件ANSYS自帶混凝土開裂分析模塊，分析了軌道板在不同荷載工況組合下的混凝土開裂情況，結果表明：單獨列車荷載或者正溫度梯度作用條件下軌道板混凝土裂紋甚微，列車荷載與負溫度梯度共同作用使軌道板混凝土裂紋現(xiàn)象最嚴重，其對軌道板結構抗裂設計具備一定的參考價值。

CRTSⅡ型軌道板; 混凝土; 有限元分析

橋上CRTSⅡ型板式無砟軌道結構體系主要應用在京津、京滬、寧杭等設計時速為350 km·h-1高鐵線上，軌道結構分布地域較廣。在運營過程中受到列車荷載與環(huán)境荷載共同作用下，軌道板頂面扣件附近以及底面板角處出現(xiàn)了較為嚴重的開裂現(xiàn)象[1]，降低軌道板整體性能，剛度降低，影響列車運行安全與舒適性等[2]。目前設計規(guī)范[3]給出如下式所示的軌道板抗裂檢算公式：

-σ≤f(1)

其中：-作用標準組合在抗裂驗算邊緣的混凝土法向應力；σ-扣除全部預應力損失后在抗裂驗算邊緣混凝土的預壓應力；f-混凝土抗拉強度標準值。

而軌道板與底座板之間采用低彈模砂漿層銜接，軌道板上方受扣件與無縫鋼軌的約束等，梁軌作用機理較為復雜，因而、σ的解析表達式并未給出。為了全面地分析軌道板開裂機理及最不利位置等，相關研究者們借助有限元分析技術，開展了軌道結構混凝土拉壓應力計算及開裂研究。蔡小培和高亮等人[4]通過建立橋上縱連板式無砟軌道無縫線路縱-橫-垂向空間有限元模型，得出：滑動層摩擦系數(shù)越大，軌道板縱向力越大，軌道板出現(xiàn)裂縫的幾率就加大；李東升和牛斌等人[5]建立了CRTSⅡ型板式無砟軌道三維實體有限元模型，探討了當梁體從0 ℃升或降20 ℃軌道底座板縱向與橫向的拉、壓應力變化；文獻[6]得出：設計荷載300 kN條件下，軌道板最大拉應力與最大壓應力均小于允許應力，因而在受到豎向列車荷載作用下軌道板不會產生開裂以及壓碎破壞現(xiàn)象，據(jù)此對軌道板強度進行了校核；文獻[7]借助有限元分析技術，在列車荷載作用下，得出軌道板板底縱向拉應力遠小于橫向拉應力，且均小于允許應力值，縱橫向拉應力最大值發(fā)生位置（最不利位置）在板腳處，最大壓應力發(fā)生在荷載正下方，按照式(1)計算得到軌道板不產生裂紋；文獻[8]定性的分析了軌道板裂縫產生的原因包括：列車荷載、溫度作用以及材料自身的物理性能參數(shù)(水灰比、材料級配)。

國外關于無砟軌道軌道板開裂驗算的研究甚少，且均未考慮多種工況組合下的軌道板開裂驗算，因此，本文借助ANSYS大型通用軟件，建立了橋上無砟軌道結構實體有限元模型，通過軟件中自帶混凝土開裂分析模塊，分析了多種荷載工況組合下的軌道板不同位置處的混凝土開裂。

1 模型建立

橋上CRTSⅡ型板式無砟軌道結構體系包括：無縫鋼軌、扣件、CRTSⅡ型軌道板、底座板、砂漿層等構件，本文建立單塊軌道板長度的無砟軌道結構體系實體有限元分析模型。鋼軌采用beanm188梁單元模擬；扣件采用combin14線性彈簧單元模擬；底座板、砂漿層、軌道板俊才有solid65單元模擬；軌道板上下層鋼筋均采用Link8單元模擬；橋面支撐采用combin14線性彈簧單元模擬，考慮到單塊軌道板縱向連接以及底座板縱連，因而軌道結構兩端節(jié)點均采用全約束方式，同時考慮到砂漿層與底座板跟軌道板實際接觸與受力，將砂漿層與其界面的摩擦系數(shù)為0.35。整個結構體系模型的所有接觸面均采用界面單元進行剛性連接，鋼筋與混凝土不考慮相對滑移，因而采用整體式建模方式，分別如圖1與圖2所示。各構件單元類型與幾何尺寸如下表1與表2所示。

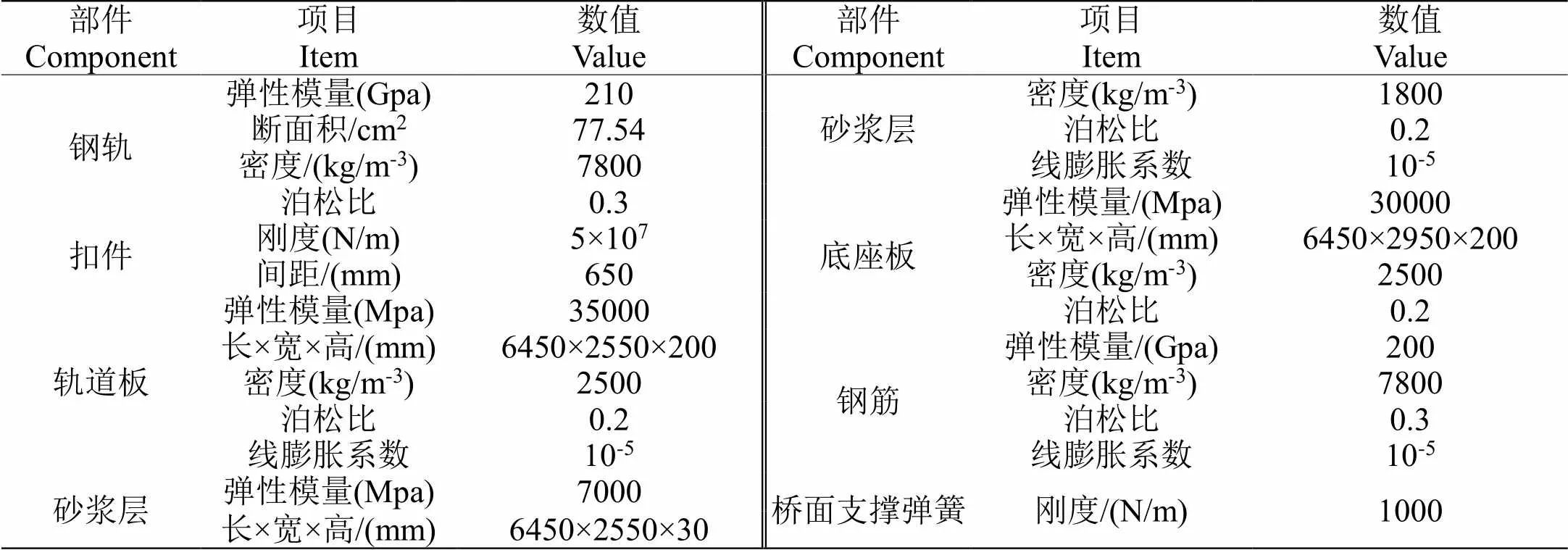
表 2 各構件幾何尺寸及材料性能參數(shù)

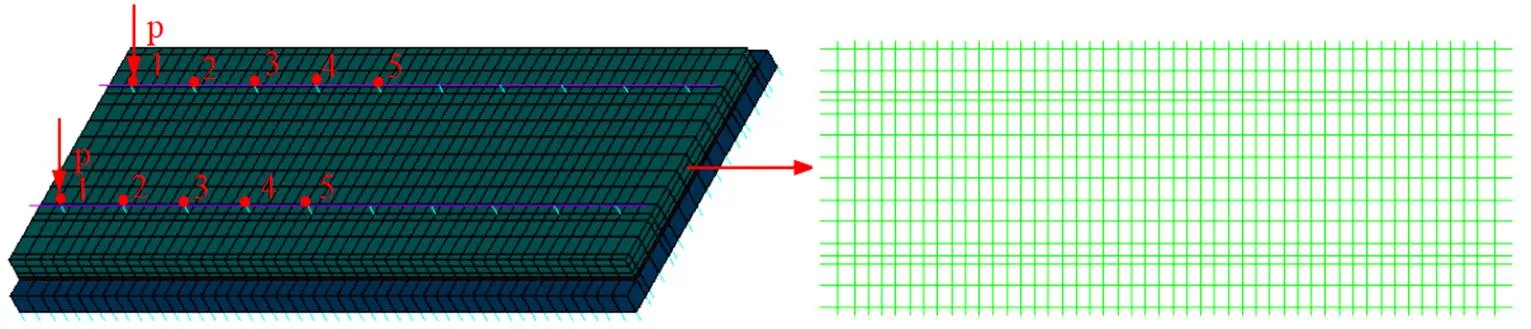
圖 1 橋上軌道結構體系有限元模型　　　　圖 2 軌道板上、下層鋼筋布置

2 荷載工況分析

整個軌道結構體系底面都為連續(xù)支撐，因而自身重力作用效應不明顯，目前設計規(guī)范[1]建議橋梁段單元式軌道結構荷載主要考慮列車荷載與溫度梯度作用。

2.1 列車荷載作用

趙磊[9]基于有限元模型，當列車荷載作用于不同扣件處時(扣件正上方)，分析了路基段與橋梁段的軌道板混凝土拉、壓應力，砂漿層豎向壓應力；類似地，孫旭[10]通過有限元模型亦得出軌道板最大拉應力值，兩者均認為：不考慮鋼筋效應的軌道板在單一列車荷載作用下，軌道板混凝土最大拉應力均小于允許應力，不會產生裂縫，而實際工程中，鋼筋與混凝土的協(xié)調工作，對整個軌道結構的應力的分布有一定影響。本文有限元模型分析結果如下圖3與圖4所示。

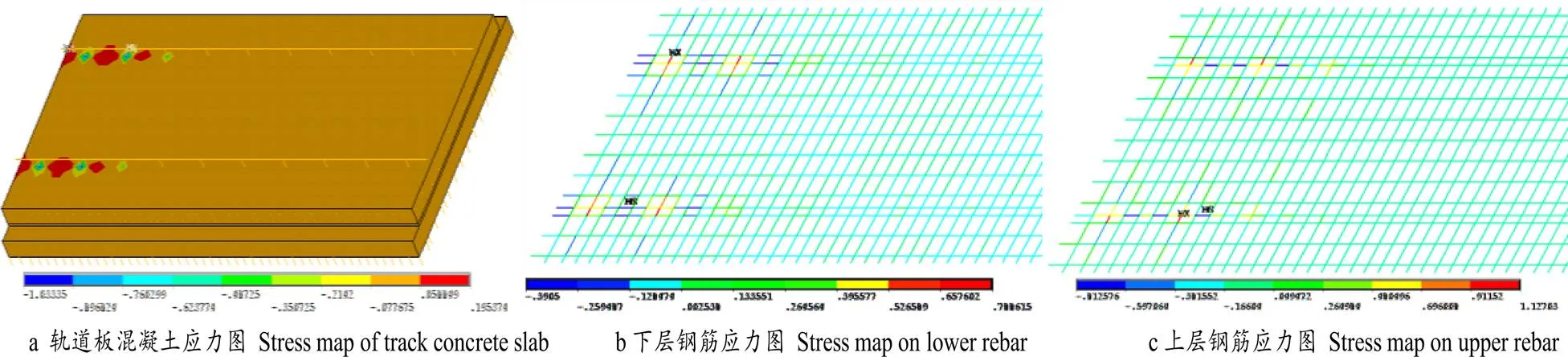
圖 3 列車荷載作用下軌道板及鋼筋應力云圖(列車荷載作用于扣件1)

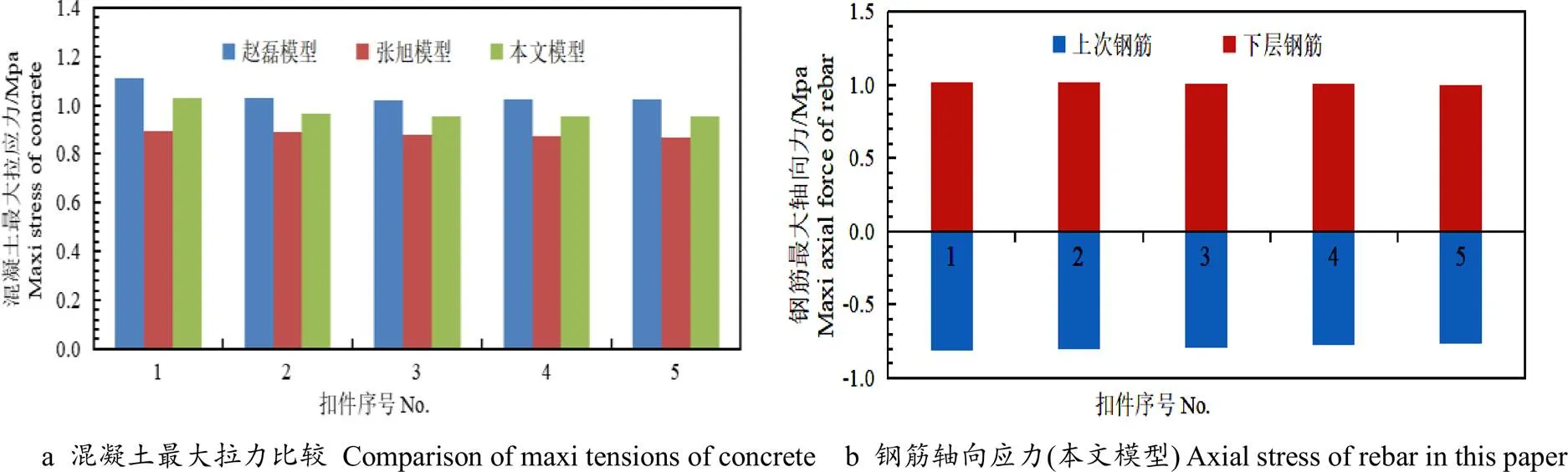
圖 4 列車荷載作用下各有限元分析模型對比

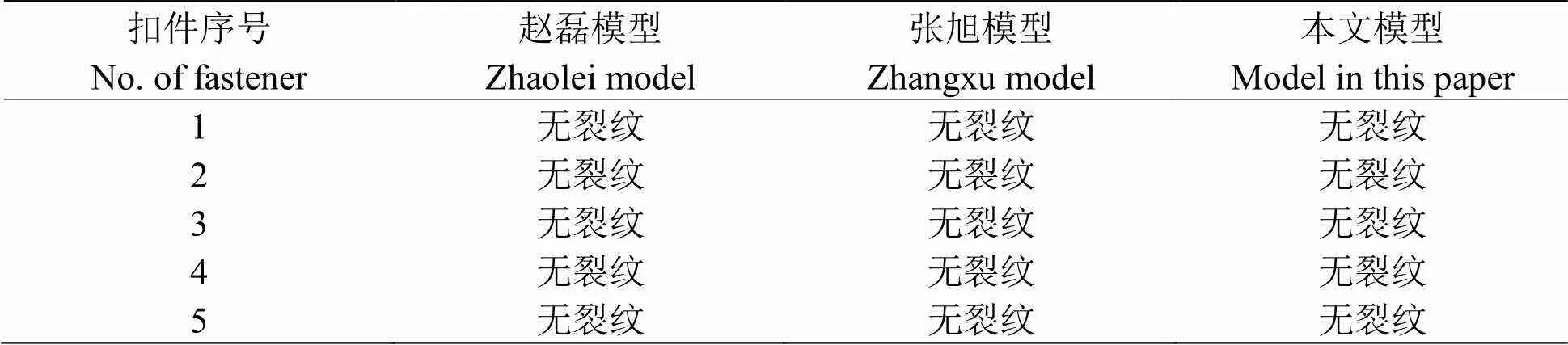
表 3 不同有限元分析模型下的裂紋分布

圖 5 列車荷載作用下裂紋分布圖

圖3與圖4表明：本文軌道結構有限元分析模型得出列車荷載影響到的范圍大致為前后兩個扣件間距，鋼筋軸向力發(fā)生在相應荷載作用扣件處的正下方，上層鋼筋以受壓為主，下層鋼筋以受拉為主，鋼筋最大軸向應力遠小于鋼筋屈服應力，軌道板混凝土最大應力與其余研究者們的研究結論大體接近，因而在單一列車荷載作用下，鋼筋作用對混凝土最大拉、壓應力“貢獻”并不大。同時，列車荷載作用在不同的位置時，軌道板混凝土最大拉應力均發(fā)生在扣件正下方位置處(負為受壓、正為受拉)，且均小于允許應力值2.57 Mpa；圖5表明：列車荷載作用于不同位置時，軌道板混凝土任意位置均未出現(xiàn)裂縫，混凝土最大拉應力變化均不大。將單一列車荷載作用時的軌道板裂紋變化情況整理成表3所示。

2.2 溫度荷載作用

相關研究者們針對軌道板溫度荷載已經做了大量的研究[10-13]，由于溫度作用引起的軌道板變形會受到砂漿層以及鋼軌等的多方位約束作用，此時軌道板會產生溫度應力。軌道板主要承受三種溫度應力作用[14]：溫度梯度產生的翹曲應力、溫度整體升降產生的軸向拉壓力，分別如圖6所示。

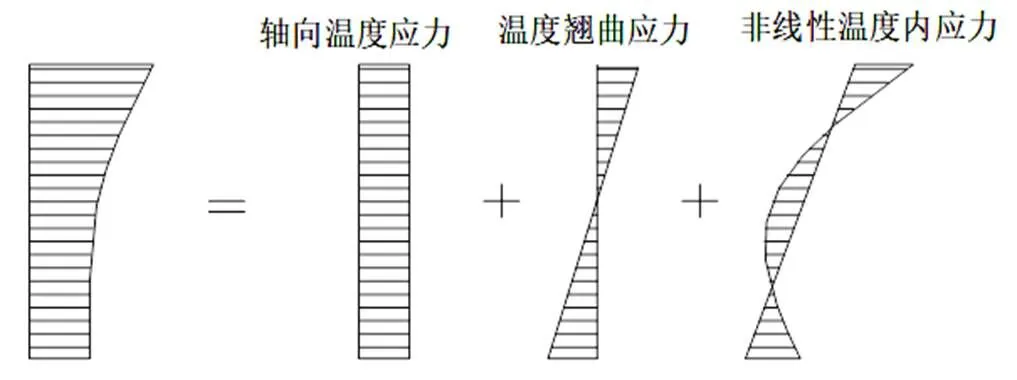
圖 6 軌道板溫度應力組成示意圖

這三種溫度力都對軌道板混凝土裂紋的形成與開展造成了一定影響，其中溫度梯度作用力尤為明顯，對混凝土裂縫開展“貢獻”最大[15]，因而本文著重探討溫度翹曲應力。本文考慮軌道板上下表面溫差分別為±10 ℃這兩種溫度荷載工況(砂漿層、底座板鑲嵌于軌道板與橋面之間，與外界熱交換較少，因而本文不考慮底座板與砂漿層的溫度梯度作用)，本文模型分析結果分別如圖7與圖8所示，不同模型分析結果對比如圖9所示。

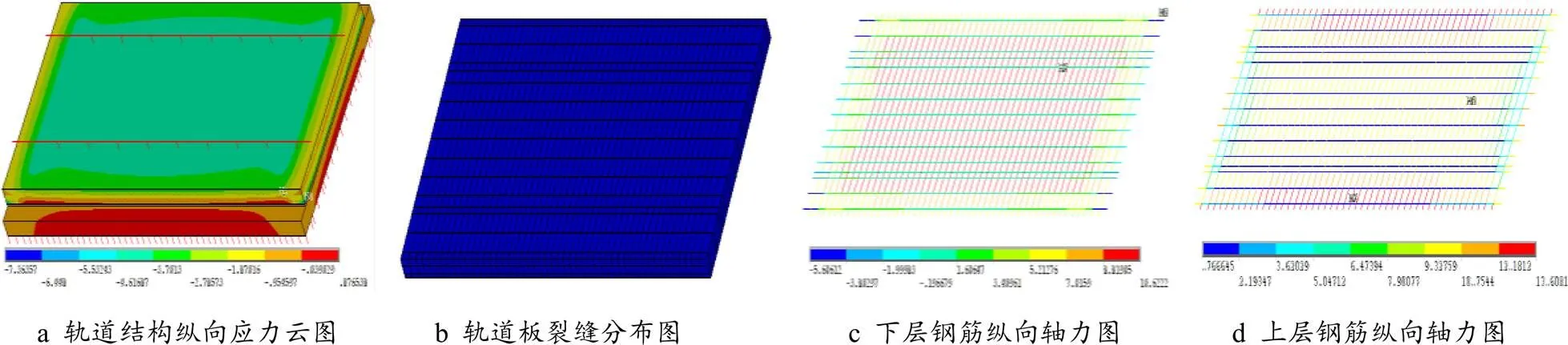
圖 7 上下表面溫差+10℃混凝土裂紋分布與鋼筋軸向力圖

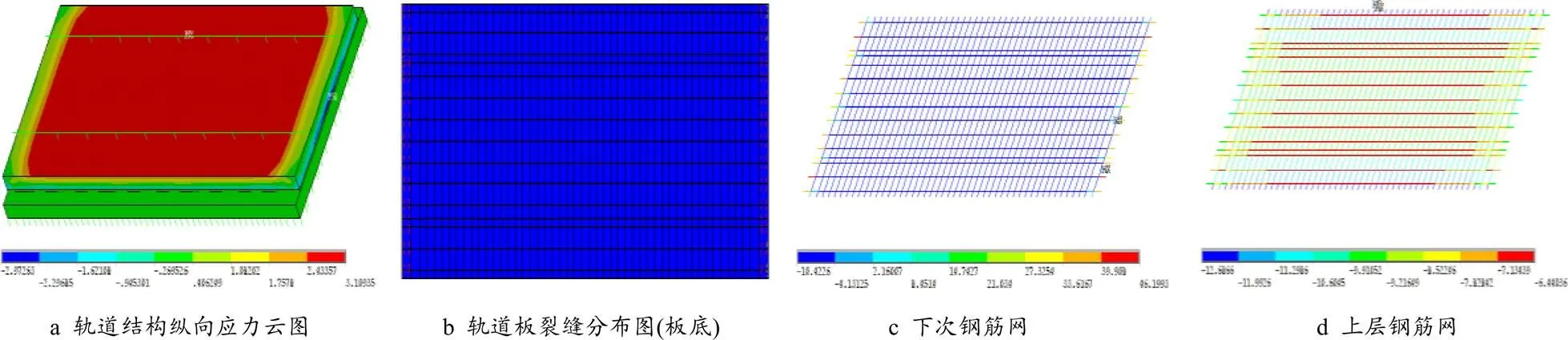
圖 8 上下表面溫差-10 ℃混凝土裂紋分布與鋼筋軸向力圖

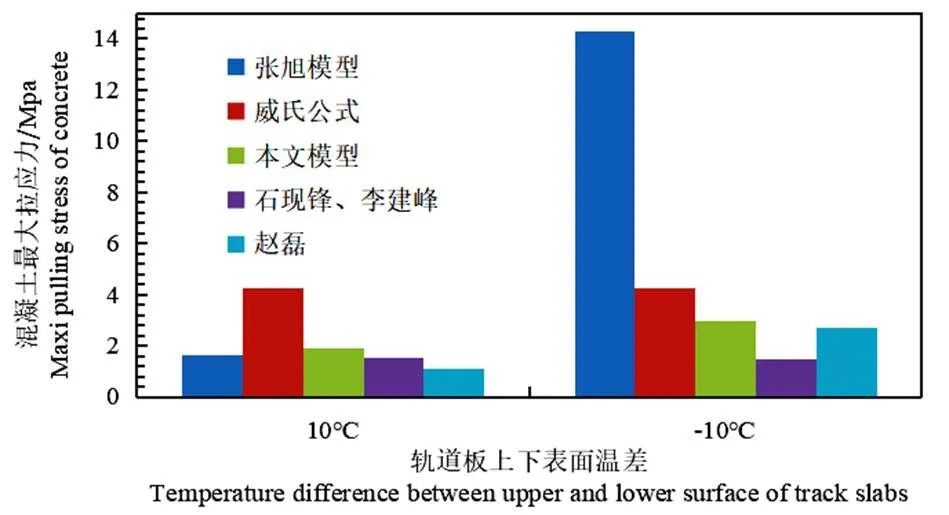
圖 9 不同模型下溫度梯度效應分析結果對比

從左圖9可以看出：張旭[10]建立的軌道板有限元應力分析模型在負溫度梯度時，其結果相差最大，因為其將砂漿層、底座板這兩層實體結構均簡化成彈簧作用，忽略了砂漿層對軌道板以及底座板的約束與協(xié)調作用；趙磊模型與石現(xiàn)峰模型中由于其忽略了軌道板上下層鋼筋網的作用，其分析結果亦存在較大誤差，本文模型較大程度上避免了上述研究者們的模型缺陷(考慮鋼筋作用以及各構件層的約束與協(xié)調作用)，因而本文模型也更接近工程實際情況，所求解的軌道板縱向最大拉應力與威氏公式數(shù)值解均較為接近，且最大值均發(fā)生在板底面與板頂面；據(jù)圖7-b知：+10 ℃時，軌道板幾乎沒有裂紋；根據(jù)圖8-b得知：在-10 ℃時，軌道板板端底部存在較多的裂紋，較單一列車荷載(300 kN)而言，-10 ℃對軌道板裂紋的形成“貢獻”更大。軌道板受溫度梯度作用時，上下層鋼筋在溫度梯度作用下軸向拉壓應力遠小于屈服應力，同時軌道板應力變形以及裂紋狀態(tài)關于縱向或者橫向中性軸大致成對稱狀態(tài)。根據(jù)混凝土最大拉應力值與允許應力關系，本文將不同分析模型的軌道板裂紋分布情況歸納如下表4所示。

表 4 軌道板混凝土裂紋分析模型對比

2.3 溫度荷載與列車荷載共同作用

與前述章節(jié)所言，本文考慮列車豎向荷載(300 kN)與溫度梯度的組合作用，二者均為軌道板開裂的主要影響因素，兩者共同作用下，軌道板受力更為復雜，目前對于溫度和列車荷載共同作用引起的軌道板裂紋研究較少，張旭模型[10]考慮軌道板表面上下溫差為-5 ℃時，對軌道板開裂狀態(tài)進行了一定探討，得出：列車荷載與溫度梯度共同作用引起的軌道板裂紋較單一荷載條件下多。而如上述章節(jié)所言，張旭模型[10]軌道結構實際受力存在較大差距，同時我國幅員遼闊，影響無砟軌道結構的環(huán)境差異較大，因而本文考慮列車豎向荷載(300 kN)溫度梯度為±10 ℃時的荷載工況組合，分析結果如下圖10與圖11所示。

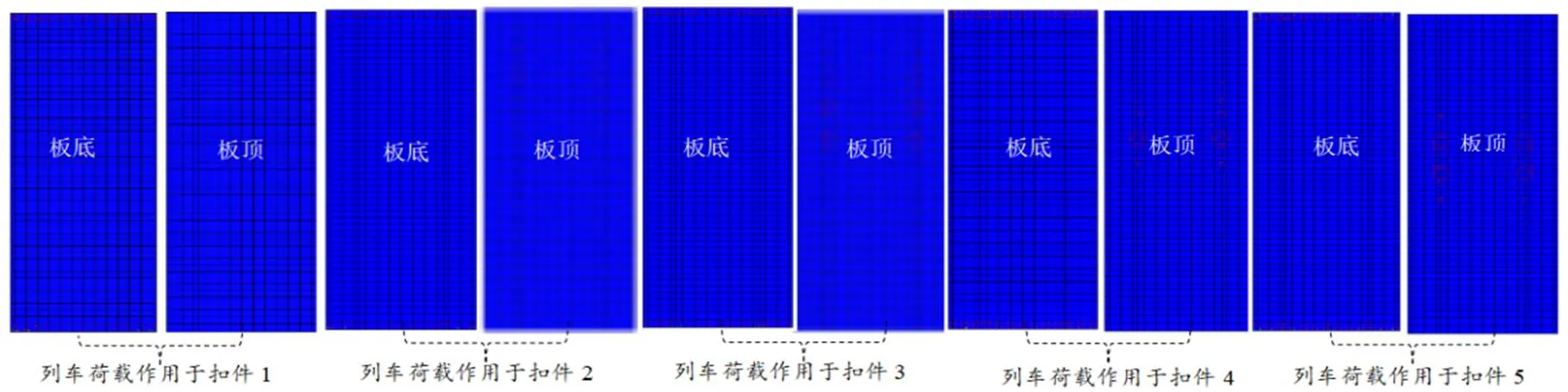
圖 10 列車荷載+負溫度梯度工況(-10 ℃)時軌道板裂紋分布圖

圖 11 列車荷載+正溫度梯度工況(+10 ℃)時軌道板裂紋分布圖

從圖10得知：軌道板處于負溫度梯度與不同位置處的列車荷載作用耦合時，軌道板板端處底面裂紋分布、條數(shù)等基本不變，由于列車荷載效應傳遞至軌道板底部的拉應力并不明顯，因而板角處混凝土開裂狀態(tài)受溫度梯度影響最大；軌道板處于負溫度梯度作用時軌道板下凹變形會受到外界約束，軌道板上表面會產生拉應力作用，此時當列車荷載作用在不同扣件正下方處時，此處混凝土會產生拉應力作用，與負溫度梯度作用“疊加”，因而此時扣件周遭混凝土裂紋分布較單一荷載作用時更為密集。

從圖11得知：軌道板處于正溫度梯度與不同位置處的列車荷載作用耦合時，軌道板上拱變形受阻，板頂產生壓應力，板底產生小于允許值的拉應力。同時，列車荷載作用傳遞至軌道板底部混凝土的拉應力較小，因而此時軌道板底部裂紋均較少；列車荷載作用在扣件下方周遭混凝土產生的拉應力與正溫度梯度產生的混凝土壓應力“相減”，因而軌道板頂面混凝土裂紋亦甚少。同時軌道板裂紋分布狀態(tài)關于軌道板縱向或者橫向中心線呈現(xiàn)出一定的對稱性，這主要是由于實際列車荷載作用與溫度梯度作用對稱性引起，上述分析結果與工程實際較為吻合[16]。

3 結論

（1）軌道結構在單一列車荷載作用下，與其余研究者們所建立的有限元分析模型分析結果較為接近，均無明顯裂縫，可見列車荷載對軌道板裂縫貢獻不大。為了盡可能模擬實際結構受力狀態(tài)，本文按照軌道板結構設計，考慮上下鋼筋網片的布置，分析結果表明：鋼筋作用對軌道板混凝土所受拉壓應力影響不大，而出于軌道板構件按照抗彎構件進行設計，鋼筋網片亦成了必不可少的部分；

（2）由于軌道板的翹曲變形會受到砂漿層、扣件等的多方位約束作用，此時軌道板會產生較大的溫度應力，溫度梯度作用下的混凝土拉壓應力較列車荷載作用更為明顯，本文亦比較了幾種溫度梯度作用分析模型，得知：本文計算結果與威氏公式解析解更為接近，正溫度梯度作用下，軌道板混凝土呈上壓下拉受力狀態(tài)，而拉應力均小于允許應力，混凝土未出現(xiàn)裂紋現(xiàn)象。負溫度梯度作用下，軌道板底面板角處均出現(xiàn)不同程度的裂紋；

（3）軌道板處于溫度梯度與列車荷載共同作用時，軌道板混凝土拉壓應力較單一荷載條件下變化較大：負溫度梯度與列車荷載共同作用時，兩者在軌道板頂面產生的拉應力相疊加，造成了軌道板表面裂紋現(xiàn)象較為明顯。反之，由于列車荷載作用傳遞至軌道板底面混凝土拉應力較小，因而在正溫度梯度與列車荷載作用下的軌道板混凝土裂紋現(xiàn)象不明顯。同時在以上荷載工況組合下，軌道板裂紋分布大致關于縱、橫向中心軸呈對稱狀態(tài)；

（4）本文研究范圍停留在列車荷載與溫度梯度的“瞬時效應”，忽略了混凝土損傷累積效應，當軌道板處于正、負溫度梯度反復交替循環(huán)作用下，應力幅會使得混凝土處于疲勞累積損傷狀態(tài)，隨著服役時間增加，軌道板裂紋會愈加嚴重，因而本文基于“瞬時效應”的研究成果有待于進一步發(fā)展。

[1]賀志榮,賈德華,楊格.高速鐵路CRTSⅡ型軌道板裂縫分析與預防[J].鐵道建筑,2011(9):115-118

[2]劉學毅,趙坪瑞,楊榮山.客運專線無砟軌道設計理論與方法[M].成都:西南交通大學出版社,2010:94-95

[3]中國鐵路總公司.Q/CR 9130-2015鐵路軌道極限狀態(tài)法設計暫行規(guī)范[S].北京:中國鐵道出版社,2015

[4]蔡小培,高亮,孫漢武,等.橋上縱連板式無砟軌道無縫線路力學性能分析[J].中國鐵道科學,2011,32(6):28-33

[5]牛斌,胡所亭,李東昇,等.長大溫度跨混凝土橋上CRTSⅡ型板式無砟軌道的力學性能研究[J].中國鐵道科學,2016,37(3):22-29

[6]孫璐,段雨芬,楊薪.高速鐵路CRTSⅢ型板式無砟軌道結構受力特性研究[J].鐵道工程學報,2013,182(11):32-39

[7]劉成軒,翟婉明.軌道板強度問題的有限元分析初探[J].鐵道工程學報,2001,18(1):24-26

[8]王森榮,楊榮山,劉學毅,等.無砟軌道裂縫產生原因與整治措施[J].鐵道建筑,2007(9):76-79

[9]趙磊.高速鐵路CRTSⅡ型板式無砟軌道結構失效分析與傷損試驗研究[D].南京:東南大學,2017:154-159

[10]孫旭.CRTSⅡ型軌道板裂縫產生與裂縫擴展規(guī)律研究[D].石家莊:石家莊鐵道大學,2017:40-45

[11]史克臣CRTSⅡ型板式軌道施工過程中軌道板受力特性分析[J].鐵道建筑,2013(9):120-122

[12]石現(xiàn)峰,李建斌.溫度對板式無砟軌道結構的影響研究[J].鐵道工程學報,2008,116(5):30-33

[13]王繼軍,尤瑞林,王夢,等.單元板式無砟軌道結構軌道板溫度翹曲變形研究[J].中國鐵道科學,2010,31(3):9-14

[14]歐祖敏,孫璐.高速鐵路無砟軌道板非線性溫度效應簡化計算方法[J].鐵道學報,2015,37(6):79-87

[15]徐慶元,孟亞軍,李斌,等.溫度梯度作用下縱連板式無砟軌道疲勞應力譜[J].中南大學學報(自然科學版),2015,42(2):736-741

[16]余志武.高速鐵路無砟軌道-橋梁結構體系經時行為研究[R].長沙:中南大學高速鐵路建造技術國家工程實驗室,2016

Analysis on Concrete Crack of Track Slab CRTSⅡ under Different Load Conditions

YANG Yan

617000,

The present studies related the crack of track slab are confined to the special location and leave the load combinations be out of consideration, meanwhile. The proposed equation by design code which is used to express the limite state of crack of track slab is not detailed. This paper took advantage of ANSYS software to analyze the crack being in different location of track slab which was in situation of load combinations, the result showed that the single load such as train load or temperature gradient could hardly make the track slab cracked, the train load combine the negative temperature gradient would make the crack of track slab more serious. All of these could provide the references to the crack resistance of track slab.

Track slab CRTSⅡ; concrete; Finite element analysis

U452.21

A

1000-2324(2021)01-0109-06

10.3969/j.issn.1000-2324.2021.01.019

2019-02-08

2019-03-24

攀枝花市科技計劃項目:高鈦渣輕型空心疊合板在裝配式結構中的應用研究(2018CY-G-20)

楊艷(1979-),女,碩士,講師,研究方向:道路工程. E-mail:pzh_yangyan@126.com

網絡首發(fā):http://www.cnki.net