基于改進的BP 神經網絡膠鉚接頭的力學性能預測研究

劉文杰，邢彥鋒，陸瑤

（201620 上海市 上海工程技術大學 機械與汽車工程學院）

0 引言

由于輕型材料與鋼板的混合連接能夠有效降低車身質量，提高汽車的燃油經濟性能與汽車動力性能，已成為今后車身結構的發展方向[1]。自沖鉚接技術具有工藝簡單、外觀美觀等特點[2]，廣泛應用于異種材料的連接。將結構膠接與自沖鉚接技術結合形成的膠鉚技術應用于車身連接中，既可以改善膠接技術的裂縫延伸、瞬間失效等問題，也緩解了鉚接導致的集中應力過大、連接強度不穩定等問題[3]。

針對自沖鉚接及膠鉚工藝，國內外學者進行了大量研究。Fabrizio[4]對比了鋁合金自沖鉚接、膠接及膠鉚接頭的力學性能，發現低循環次數下，混合接頭的性能比普通膠接接頭差，而高循環次數下，混合接頭的性能要好得多。并且，相對于粘結接頭，混合接頭中機械緊固的存在顯著降低了粘合劑層中的裂紋擴展速率，因此疲勞壽命更長；劉洋[5-6]等制備了5052 鋁合金以及鈦合金和8090 鋁鋰合金的自沖鉚接單搭接接頭和粘接-自沖鉚復合接頭，通過力學試驗獲得各組接頭的失效載荷，并計算了各組接頭的能量吸收值，發現粘接劑可以提升自沖鉚接接頭的力學性能；周江奇[7]等研究了結構膠對自沖鉚接接頭成型過程的影響規律，發現結構膠能夠在接頭成型過程中減小鉚釘的鉚接力，使得膠鉚接頭的擴張程度小于自沖鉚接接頭；李明彬[8]等制作了一種新型耐高溫復合材料2D-C/SiC 的膠鉚接頭，并研究了不同搭接寬度下接頭的力學性能，發現接頭失效模式均為膠層截面破壞以及鉚釘剪切破壞，且膠層界面首先發生開裂。

反向傳播神經網絡，簡稱BP 神經網絡（BPNN），這是一種基于誤差反向傳播的多層前饋網絡，該算法在求解非線性連續函數時，通過不斷改善多層前饋神經網絡權重，能夠快速有效地逼近原始結果[9-11]，但會存在一些缺陷：（1）學習收斂速度慢；（2）局部極小問題；（3）網絡結構選取尚無理論依據，只能根據經驗選取。遺傳算法（Genetic algorithm）是模擬自然界遺傳機制和生物進化論而成的一種并行隨機搜索最優化方法[12-14]。該算法從多個初始點并行運行，能夠改善BP 神經網絡的訓練缺陷。

目前，膠鉚接頭的質量評價方法主要為破壞性試驗和在線監測[15]方法，不具有可預測性，因此，尋找一種可靠的膠鉚接頭的質量預測模型具有較大意義。本文利用遺傳算法優化BP 神經網絡的連接權值和閾值，并將遺傳算法改進的BP 神經網絡（GA-BPNN）應用于膠鉚接頭的力學性能預測中，建立了膠鉚接頭最大拉剪力預測模型，最后通過試驗驗證了該模型的精確度。

1 膠鉚連接的工藝過程

膠鉚工藝是在鉚接之前使用膠粘劑對工件進行粘接，之后再使用鉚接工藝進行鉚接，包括表面處理、涂膠、鉚接、固化4 個步驟進行。其中的鉚接步驟為普通的鉚接工藝，用于連接兩種或兩種以上金屬板材的冷機械連接工藝。鉚接工作過程為：首先將壓邊圈及鉚釘下降到與板件接觸的位置，將板件夾緊固定；然后在動力的推動下，沖頭下降，推動鉚釘刺穿；接著鉚釘被進一步推入板件，鉚釘腿部張開形成機械互鎖，將板件固定在一起；最后達到預定的行程后，沖頭與壓邊圈卸載對板件的夾緊力并回到初始位置。圖1 所示為自沖鉚接工藝過程依次為夾緊、刺穿、擴張、卸載4 個階段。

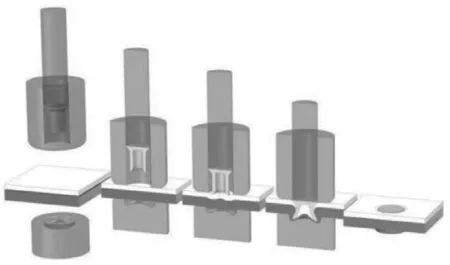
圖1 自沖鉚接工藝流程Fig.1 Self-piercing riveting process

2 膠鉚連接試驗

本研究使用的材料是AA6111 鋁合金板和DP780 高強度鋼板。板材力學性能如表1 所示。鉚釘長度為6 mm，凸臺凹模的深度為2 mm，內部底徑為8.8 mm。本文選擇的結構膠粘劑為ET5429，膠粘劑具體屬性如表2 所示。

表1 板材力學性能Tab.1 Mechanical performance of the plates

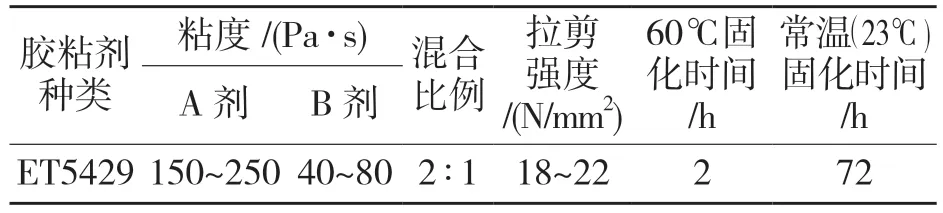
表2 膠粘劑物理屬性Tab.2 Adhesive physical properties

使用的液壓鉚接設備如圖2（a）所示。膠鉚試樣如圖3 所示，使用的疊加組合為上層鋼板+下層鋁板，紅色陰影為涂膠區域，膠層厚度為0.1 mm，在涂膠時，撒上直徑為0.1 mm 的玻璃珠控制膠層厚度。使用萬能拉伸試驗機對接頭拉伸力進行測量，拉伸速率為0.5 mm/min，如圖2（b）所示。進行拉伸試驗時，夾持寬度為30 mm，并在試件兩端添加了相同厚度的墊片，以保證實驗時拉伸力方向與板料保持平行。

圖2 鉚接及拉伸實驗設備Fig.2 Self-piercing riveting and tensile testing machine

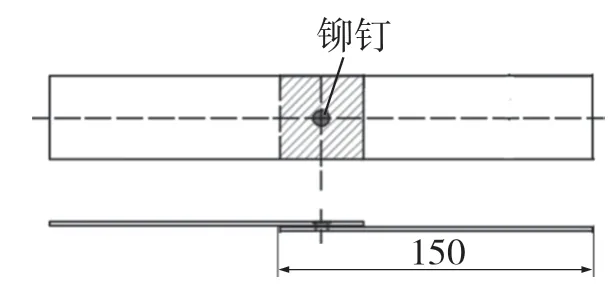
圖3 膠鉚接頭試樣Fig.3 Riv-bonding joint sample

3 GA-BP 神經網絡預測模型

3.1 算法參數的確定

由于GA-BP 神經網絡是在BP 神經網絡模型的基礎上改進的，因此，需要構建基于BP 神經網絡的膠鉚接頭力學性能預測模型。神經網絡參數包括神經元個數、隱含層數、隱含層神經元個數及傳遞函數等。

BP 神經網絡結構包含1 個輸入層、1 個或多個隱含層和1 個輸出層。結合膠鉚接頭力學性能的課題，輸入層中神經元個數為3，分別為鉚接壓強、搭接寬度和鋁板厚度。輸出層神經元個數是1，為膠鉚接頭最大拉剪力。隨機改變鉚接壓強、搭接寬度和鋁板厚度，共獲得了100 組膠鉚接頭的最大拉剪力，其中部分數據如圖4 所示。

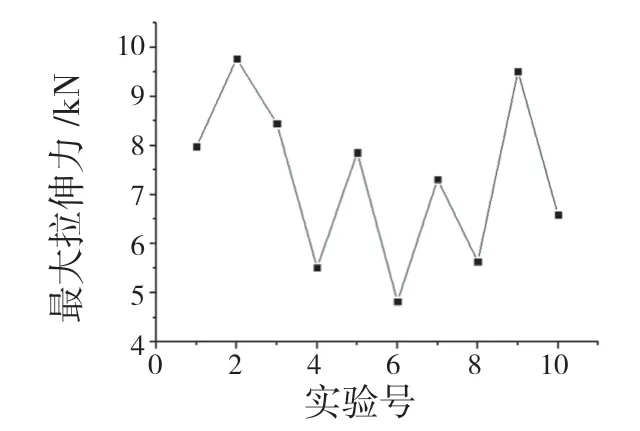
圖4 最大拉剪力部分數據Fig.4 Partial data of maximum tensile force

在數據訓練之前，首先使用式（1）對數據進行歸一化處理。

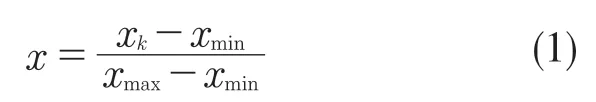
式中：xmin——數據序列中的最小數；xmax——數據序列中的最大數。

歸一化處理后，將前90 個數據作為訓練樣本，用來訓練適合應用于分析膠鉚參數和膠鉚接頭最大拉剪力的關系的預測模型，后10 個數據作為測試樣本，用來驗證所獲得的膠鉚接頭最大拉剪力預測模型。

本文采用經典三層網絡結構，即隱含層只有一個。隱含層節點數是決定BP 神經網絡預測精度的關鍵因素，從而決定了膠鉚接頭最大拉剪力的預測精度。通常帶有單個隱層的神經網絡確定隱含層中神經元數量可以使用經驗式（2）進行計算。通過式（2）計算隱含層神經元個數在3～13 之間。因此，本文不斷改變隱含層神經元數目，并代入神經網絡訓練，得到在不同隱含層神經元個數下的均方誤差如圖5 所示。

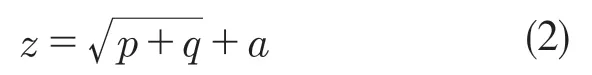
式中：p，q——輸入層和輸出層中的節點數；a——取值范圍為1～10 的常數。

從圖5 中可以看出，當隱含層神經元個數為5 個時，均方誤差最小，因此，本文所選擇的隱含層神經元個數為5。本文的膠鉚接頭最大拉剪力預測模型網絡結構如圖6 所示。

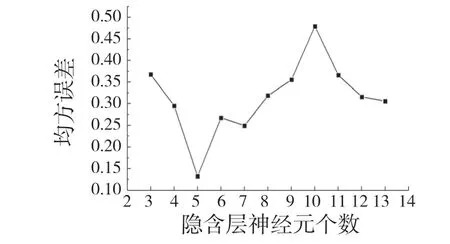
圖5 3 層BP 網絡的訓練Fig.5 Three-layer BP network training

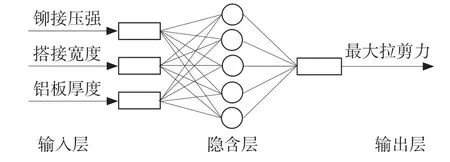
圖6 預測模型網絡結構Fig.6 BP neural network structure

遺傳算法參數對遺傳算法的運算精度有著重要影響，算法參數主要包括編碼長度、適應度函數選擇、選擇操作、交叉操作、變異方法、種群數目、最大進化次數選取等，具體選擇如下所示：

（1）編碼長度確定。采用浮點數編碼，個體長度即染色體長度計算公式如式（3）所示。經過計算本文S=3×5+5×+5+1=26。

（2）適應度函數選擇。為使預測值和實際值之間的殘差盡可能小，選擇預測樣本的預測值和實際值之間的絕對誤差之和作為目標函數的輸出。適應度函數使用式（4）進行計算。

（3）選擇操作。采用隨機遍歷抽樣作為選擇算子。并采用輪盤賭法選擇競爭成功的個體。

（4）交叉操作。采用單點交叉作為交叉算子。在個體代碼串中，僅隨機選擇一個交點，并且在該點交換兩對個體的編碼部分。

（5）變異操作。使用變異公式對基因進行變異[10]。

（6）種群數目選取。種群規模越大，代表可同時處理更多數據。一般來說，種群數目取20～100 之間。本文經多次試驗，種群數目取60。

（7）最大進化次數選取。最大進化代數作為一種模擬終止條件，一般視具體問題而定。本文中的最大進化次數取100。

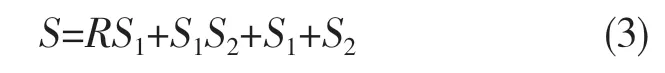
式中：S——染色體長度；R——輸入層神經元個數；S1——隱含層神經元個數；S2——輸出層神經元個數。

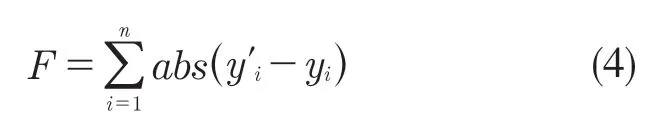
式中：F ——適應度函數；n ——網絡輸出節點數；yi——BP 神經網絡中第i 個節點的實際結果；y'i——第i 個節點的預測結果。

3.2 BPNN 與GA-BPNN 訓練結果

BP 神經網絡與GA-BP神經網絡模型結構為3-5-1，即3 個輸入層神經元，5 個隱含層神經元，1 個輸出層神經元。將準備好的100 組數據分別代入準備好的BP神經網絡及GA-BP 神經網絡程序中，對神經網絡進行訓練，訓練在MATLAB 中實現。

圖7 為BPNN 與GABPNN訓練過程的性能比較。由圖7可見，BPNN 與GABPNN 訓練曲線、驗證曲線以及測試曲線隨著迭代次數的增加而下降，最后成功收斂于預設的均方誤差；3 條曲線的走向與變化相似，且遺傳神經網絡三曲線誤差更小。圖7 中圓圈位置代表迭代停止，BPNN 在4 次迭代之后收斂結束，GA-BPNN 在8 次迭代后收斂結束。GABPNN 比BPNN的收斂時間長，這是因為遺傳算法全局尋優，且本文中預設的種群規模較大，種群進化需要較多的迭代次數。

圖8 為神經網絡模型在樣本訓練后的線性回歸結果，從圖8可以看出，BPNN 的相關系數為R=0.968 63，而GA-BPNN 的相關系數為0.979 10，說明遺傳BP 神經網絡的回歸性能更好，具有更好的泛化能力。

3.3 預測結果分析

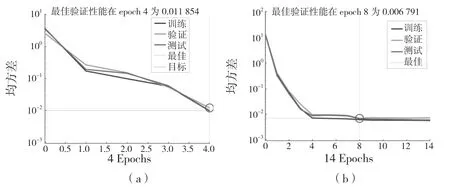
圖7 性能驗證比較Fig.7 Comparison of training performance of two neural networks

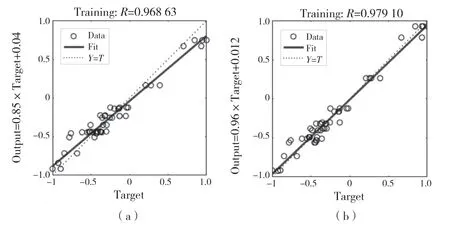
圖8 相對系數比較Fig.8 Relative coefficient of two neural networks

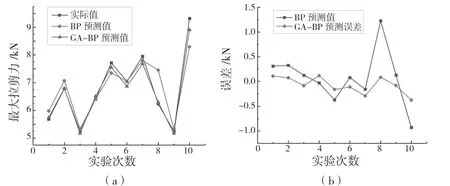
圖9 神經網絡預測結果及預測誤差Fig.9 Neural network prediction result and prediction error

將用于驗證的后10 組膠鉚接頭最大拉剪力數據分別代入訓練好的BP 神經網絡與GA-BP 神經網絡進行預測。實際值與預測結果的比較如圖9（a）所示。由圖9（a）可知，兩者預測輸出曲線與期望輸出曲線擬合效果較好，基本符合期望輸出的變化趨勢。由圖9（b）可知，BP 神經網絡與GA-BP 神經網絡誤差均在零點附近上下波動，且GA-BP 神經網絡波動幅度更小。BP 神經網絡預測誤差范圍在-0.92～1.23 kN，最大相對誤差為2.16 kN。而GA-BP 神經網絡預測誤差范圍在-0.37～0.12 kN，最大相對誤差為0.49 kN。因此，GA-BP 神經網絡的預測精度更高。

對于預測結果，可以通過均方誤差（MSE），均方根誤差（RMSE）以及平均絕對誤差（MAE）這3 個指標來評價。MSE 是實際值與預測值之差的平方的平均值，在線性回歸法中為損失函數；RMSE 是衡量觀測值與真實值之間的偏差，為機器學習模型預測結果衡量的標準；MAE 是絕對誤差的平均值，可以更好地反映預測值誤差的實際情況。

具體計算公式如下：

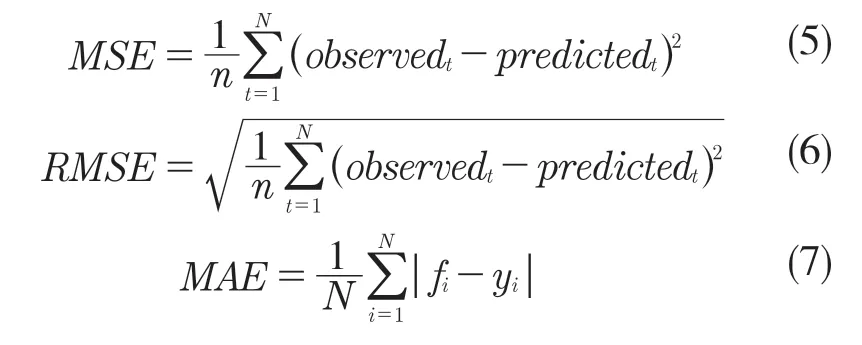
表3 列出了MSE（均方誤差），RMSE（均方根誤差)以及MAE（均值絕對誤差）。

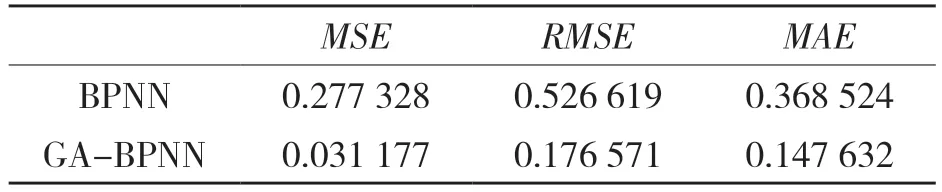
表3 3 種誤差值比較Tab.3 Comparison of three error calculation methods

從表3 可以看出，GA-BPNN 的預測精度要高于BPNN。對于這兩種模式，BPNN 的預測均值絕對誤差為0.368 524。與此相反，GA-BPNN的預測均值絕對誤差為0.1476 32，為BPNN 均值絕對誤差的40%。因此，GA-BPNN 算法比BPNN 具有更好的性能。

4 結論

使用遺傳算法改進BP 神經網絡的優化方法，通過經驗公式及試驗確定了遺傳算法和BP 網絡中的關鍵參數，建立了基于遺傳算法改進的BP神經網絡鋁鋼膠鉚接頭最大拉剪力預測模型，利用測試數據對該模型進行了驗證。結果如下：

（1）對于復雜的非線性系統，BP 神經網絡的擬合能力較差，遺傳算法多個初始點并行運行的特點彌補了BP算法易陷入局部最小值的缺點，并能夠優化BP 神經網絡的權值和閾值，從而提高預測的精度。

（2）種群的進化過程需要較長的時間，因此GA-BPNN 比BPNN 的收斂時間長，但GA-BP網絡預測相關系數更好，回歸性能更好，具有更好的泛化能力。

（3）基于BP 神經網絡與GA-BP 神經網絡的膠鉚接頭最大拉剪力預測模型均具有較高的預測精度，且GA-BP 神經網絡的預測精度更高。