多約束條件下的無人機軌跡快速規劃

吳成振，孫大運

（1.200093 上海市 上海理工大學 機械工程學院；2.200093 上海市 上海理工大學 醫療器械與食品學院）

0 引言

航空科學和現代信息技術的發展為無人機在現代戰爭中扮演重要角色提供了重要基礎，而航路規劃是實現無人機自主作戰高效能的關鍵步驟，備受國內外學者的重視[1]。目前，無人機在民用領域的應用日漸廣泛，比如無人機能夠在搶險救災、環境監測、精準農業生產、航空攝影等領域發揮巨大作用[2]。由于實際應用中復雜的飛行環境和約束條件，所以建立合理的規劃模型和高效規劃算法是無人機航跡快速規劃的一個重要內容，其核心內容為在滿足各項約束前提下，快速規劃出無人機在目標任務下的最優航跡[3]。飛行航路規劃的常見的約束條件有規劃中的導航精度約束、威脅約束、飛行器物理性能約束等，其中的部分約束條件還是相互耦合的，因而多約束問題是航路規劃的一個至關重要的問題[4]。由于無人機物理性能的限制，其定位系統會因飛行距離產生定位誤差，如果定位誤差累計超過系統允許的最大范圍就會導致任務失敗，所以，校正無人機的飛行過程產生的定位誤差是無人機航跡規劃中的一項重要任務。此外，飛行器在轉彎過程中受到自身結構限制，其轉彎過程必須存在合理的轉彎半徑，所以，在三維航跡規劃過程中，空間圓弧軌跡的處理也是一大重點。

貪心算法是求解過程相對簡單的算法，其思想是從待求解問題的初始狀態出發，由當前每一步的局部最優決策得到該算法下的全局最優解[5]。雖然貪心算法不一定得到所有問題的整體最優解，但它能得到大部分問題的整體最優解或者近似最優解[6]。因此，本文通過構造無人機在定位誤差約束下的數學模型，結合航跡點和轉彎半徑推導出空間圓弧軌跡方程，利用貪心算法對無人機的航跡進行快速規劃，結合軟件仿真得到飛行過程中的最優航跡方案。

1 多約束條件

無人機在飛行過程中，其由系統結構限制原因產生的定位誤差會隨飛行軌跡越來越大，因此在其飛行區域必須設置校正點，而校正點需在一定誤差范圍內才能成功校正誤差。校正點分為垂直和水平兩種，垂直校正點和水平校正點可校正的誤差允許范圍也不相同，且達到終點時也需要滿足誤差范圍，具體的約束條件如下：

（1）無人機從起始點到達終點的航跡長度盡可能短，經過校正點處的要校正次數盡可能少；

（2）無人機在空間飛行過程中的定位誤差有垂直誤差和水平誤差，誤差增長量均為δ個單位每米，假設當兩種誤差均小于θ個單位時，無人機仍按照預定路徑正常飛行；

（3）無人機在出發點處不存在定位誤差，其飛行過程途經垂直誤差校正點可將垂直誤差清零，水平誤差不變，途經水平誤差校正點可將水平誤差清零，垂直誤差不變；

（4）在垂直誤差校正點能夠進行校正的條件為無人機的垂直誤差不超過α1個單位且水平誤差不超過α2個單位。在水平誤差校正點能夠進行校正的條件為無人機的垂直誤差不超過β1個單位且水平誤差不超過β2個單位；

（5）無人機由于自身結構限制，其最小轉彎半徑為rmin。

2 航跡規劃模型

因為該模型要求無人機的航跡盡可能短，且通過校正點進行校正次數盡可能少，因此該問題屬于多約束條件下的最短路徑求解模型[7]。

2.1 模型建立

假設無人機經過的兩個連續校正點Pi和Pj之間的軌跡長度Dij，集合E 的元素為無人機經過的所有校正點P（ii=0，1，…，n），決策變量為xij。當xij=1 時，表示航跡連續經過校正點Pi和Pj，所有決策變量構成的集合為C，將進行校正的點Vi中的垂直校正點構成集合T，水平校正點構成集合H,并設到達校正點Pi時的累計垂直誤差為Terr（Pi），累計水平誤差為Herr（Pi），ci=1 表示該校正點進行校正，ci=0 表示經過校正點但不需要進行校正。

2.1.1 建立目標函數

根據無人機航跡軌跡盡可能短和經過校正區域進行校正次數盡可能少的要求，建立目標函數如下：

2.1.2 確定約束條件

約束條件1：飛行器到達終點的定位誤差滿足Terr（Pn）＜θ，Herr（Pn）＜θ；

約束條件2：飛行器在水平校正點能進行校正需要滿足Terr（Hi）＜β1，Herr（Hi）＜β2。

約束條件3：飛行器在垂直校正點能進行校正需要滿足Terr（Ti）＜α1，Herr（Ti）＜α2。

綜上所述，可建立飛行器在本問題約束條件下飛行器航跡快速規劃的數學模型為

2.1.3 空間圓弧軌跡求解

由于無人機存在不小于rmin的轉彎半徑，如果無人機連續經過空間的3 個校正點不共線，則該段軌跡必定存在空間圓弧，則計算該3 點形成軌跡產生的飛行誤差以及繪制飛行器軌跡時，就必須求得該段軌跡的空間圓弧的方程。空間曲線方程復雜，為避免空間幾何求解的復雜性，本文利用三點共面的性質，先將空間中每一段圓弧軌跡的求解轉換為平面幾何問題。如圖1 所示，假設無人機連續經過的3 個已知點為Pk，Pk+1（作為圓弧軌跡的切入點坐標），Pk+2，無人機選擇的轉彎半徑為rk，以Pk為坐標原點，PkPk+2為X軸建立相應的局部平面坐標系，很顯然，的長度仍為其空間上的幾何直線長度。

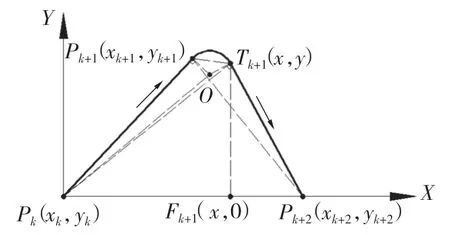
圖1 航跡平面圖Fig.1 Track plan of UAV

其中，D 可由任意一點已知坐標所決定。

根據空間距離公式可得

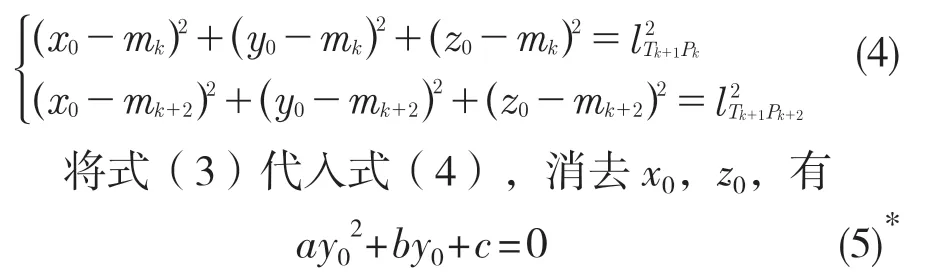
因為式（5）是根據實際幾何圖形建立的，很顯然此方程必有解，由一元二次方程求根公式可得式（5）的解為

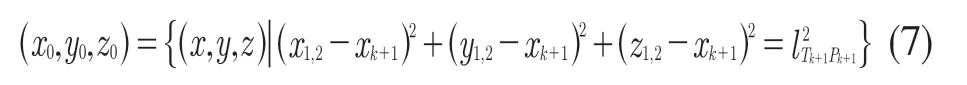
運用同樣的方法容易解得圓心Ok+1的空間坐標。因此，可求得無人機飛行軌跡存在轉彎半徑時的航跡長度以及每段圓弧軌跡的圓心坐標和圓弧軌跡的切出點坐標。

2.2 基于貪心算法的求解

貪心算法的思想是，在求解問題的過程中，對每一步都做出當前最好的判斷。本文航跡求解思想如圖2 所示。

*式（5）中：

圖2 基于貪心算法的航跡求解思想Fig.2 Model of track solving based on greedy algorithm

第1 步：在起始點 P0的可選范圍內隨機選擇一個點P1。

第2 步：以P1為圓心，結合上述的空間圓弧軌跡模型，以滿足模型約束條件的最大距離作為搜索半徑，選擇一個距離終點 B 最近的點P2作為下一步要走的點。

第3 步：判斷是否到達終點，如果沒有到達終點，計算P1和P2之間的轉彎半徑，使P1和P2兩點間的曲線長度最小，計算該段曲線中的圓弧軌跡的切出點T，令P0=T，P1=P2，轉第2 步；否則，轉第4 步。

第4 步：停止。

3 仿真實例及結果分析

因為本問題的航線軌跡是空間曲線圖而不是折線圖，為了便于軌跡的繪制，需要得到每段空間圓弧的參數方程。每段圓弧的圓心坐標Ok+1（Ox，Oy，Oz），圓弧半徑r，以及圓弧所在平面的法向量nk+1=（A，B，C）可由上文得知，則圓弧的參數方程可以表示為

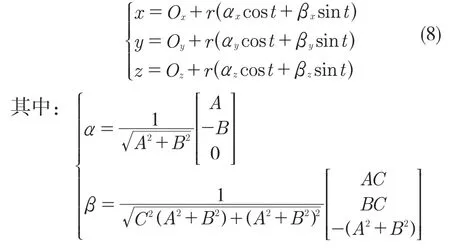
本文以“華為杯”第十六屆中國研究生數學建模競賽F 題中的附件1 校正點數據作為仿真數據，無人機最小轉彎半徑為300 m，附件1 數據的約束參數為：α1=25，α2=15，β1=20，β2=25，θ=30，δ=0.001。

基于上述模型與算法，在MATLAB 中編寫程序[8]得到的無人機飛行的校正點的數據仿真結果如表1 所示，且求得每段圓弧軌跡的轉彎半徑均為300 m，最優航跡為A-200-509-28-183-194-450-594-397-B。

表1 航跡規劃結果Tab.1 Results of UAV trajectory fast planning

圖3 為求得的航跡圖。因為各圓弧段半徑相對于兩航跡點間的距離非常小，在整體航跡圖上基本看不出圓弧軌跡，本文采用局部放大示意圖。

圖3 航跡圖及局部放大圖Fig.3 Map of UAV trajectory fast planning

礙于圖中視角以及距離比過大原因，本文求出的所有圓弧軌跡的圓心坐標以及求得的切出點坐標如表2 所示。

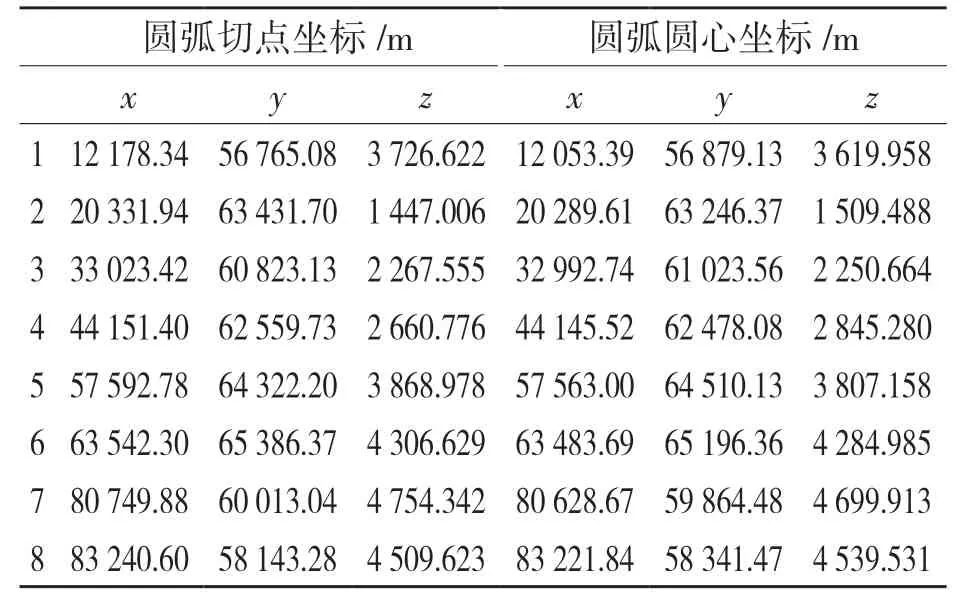
表2 圓弧軌跡圓心和切出點坐標Tab.2 Center and cut-out point coordinates of arc trajectory

4 結語

本文建立了無人機關于定位誤差的多約束條件下的飛行模型，通過推導空間曲線航跡的數學方程，解決了空間圓弧的繪制問題，利用貪心算法快速規劃出最優航跡。此外，基于此模型和算法，還可應用于倉儲物流路徑規劃領域以及車輛無人駕駛目標路徑規劃中。