參與方地位不對等條件下PPP項目風險分擔博弈研究
宿 輝,田 少 衛,馮 天 鑫
(1.吉林建筑大學 經濟與管理學院,吉林 長春 130118; 2.中核華辰建設有限公司,福建 莆田 351100)
1 研究背景
隨著我國新型城鎮化戰略的逐步推進,配套基礎設施建設的腳步也日益加快,以政府為主導的基礎設施建設已經無法滿足當前戰略發展的需要,為了解決新型城鎮化進程中配套基礎設施建設資金的巨大缺口,緩解地方政府的財政壓力,引導社會資本參與到新型城鎮化建設中來越發重要。PPP(Public-Private-Partnership)模式是政府部門和社會資本方為提供公共產品和服務,實現特定公共項目的公共效益而建立的項目全生命周期關系性契約的合作伙伴融資、建設和經營管理模式[1]。然而PPP項目的投資體量大、建設周期長等特點決定了PPP項目面臨著繁雜多變的風險[2]。政府部門工作人員認為PPP模式是將風險盡可能的轉移給社會資本方,社會資本方為了獲得PPP項目的特許運營權,不得不承擔更多的風險,一旦風險發生,社會資本方管控風險的能力比較差,最后結果可能直接導致項目失敗;而有些地區社會資本方對進入該市場并沒有太大的興趣,政府部門又急于解決財政壓力問題,為了激勵社會資本方參與PPP項目,政府部門主動承擔了更多的風險。因此,科學合理的風險分配是PPP項目規范運行的前提和公共服務滿足使用者訴求的有力保障[3]。
國內外文獻關于研究PPP項目風險分擔的方法可以分為五類:第一類是問卷調查法,如Jin等[4]和El-Sayegh等[5]通過調查問卷的形式收集數據,確定風險分擔比例,這種方法主觀性比較強。第二類是案例分析法,如李永強等[6]以蘇格蘭東部廢水處理的項目為案例,分析了項目擁有者、項目公司和投資人三方承擔的風險,但是這種方法建立在數據大量積累的基礎之上,并且僅僅局限于特定項目,不具有普遍性。第三類是數學建模的方法,如Lam等[7]運用模糊數學方法對PPP項目風險進行了量化研究,并根據風險性質進行分配,這種方法較為復雜,實用性不強。第四類是訂立合同的方法,韓傳峰等[8]認為可以通過締約合同的方式將風險進行分配,但是由于風險并不能做到完全識別,因此這種方式需要進行多次調整,并且也存在主觀性較強的缺陷。第五類是運用博弈理論的方法,如李妍[9]和李林等[10]利用非合作博弈理論的思想基于不同的視角對PPP項目共擔風險的比例進行了分析,但是沒有考慮到當社會資本參與PPP熱情不高時,政府為了吸引社會資本的注入,不得已承擔更多風險的情況。
基于以上認識,在公私雙方地位不對稱的情況下,分析當政府部門和社會資本方分別處于強勢地位時談判對風險分配的影響。本文運用動態博弈理論中不完全信息條件下的討價還價模型,對政府部門和社會部門之間風險分配的博弈過程進行分析,進而得出各方最優的風險承擔比例,以此提高私人部門參與PPP項目的積極性和促進項目的成功進行。
2 PPP項目風險分配博弈模型構建
PPP項目參與方包括地方政府、保險公司、PPP項目的投資人、融資機構等,分為政府部門和社會資本方兩類。因此,本文模型的博弈雙方為政府部門和社會資本方。在博弈過程中,首先分析當政府部門居于強勢地位時,政府部門向社會資本方轉移本應該自己承擔的風險,然后分析當社會資本方對參與PPP項目的欲望很低,而政府部門又急于引入社會資本參與進來時,社會資本方趁機轉移本應自己承擔的風險。
假設政府部門和社會資本方共同承擔同一項風險,通常政府部門先出價,如果社會資本方接受了此價格,則以談判達成而告終。如果社會資本方拒絕了政府部門的出價,則進入第二回合。由社會資本方接著出價,如果政府部門接受了社會資本方的出價,則談判結束,如果政府部門拒絕了社會資本方的出價,繼續進入第三回合。由政府部門先出價,以此類推,直至一方接受另一方的出價,談判達成結束[10]。
2.1 模型基本假設
假設一:參與方政府部門F與社會資本方N都是理性人,雙方目標都是談判達成;
假設二:PPP項目中的風險是相互獨立的,不存在關聯;
假設三:雙方之間的信息是不對稱的,即一方對另一方的行動選擇、收益函數都不能完全了解;
假設四:當政府部門居于強勢地位時,由政府部門先出價,當社會資本方部門居于強勢地位時,由社會資本方先出價,即由居于強勢地位的一方先出價。
2.2 模型參數討論
(1) 海薩尼轉換。在1967年之前,博弈論專家認為不完全信息條件下的博弈是沒辦法分析的,因為當一個參與人并不知道他在跟誰博弈時,沒有辦法定義博弈規則,之后海薩尼提出引入一個虛擬的參與人——“自然”,由“自然”首先行動決定參與人的特征,只有參與人知道自己的特征。
(2) 政府部門與社會資本方的風險轉移及概率。在不完全信息條件下的博弈中,參與方對博弈的支付(策略)并不完全清楚,這就導致雙方談判的地位并不對稱,當政府部門居于強勢地位時,會通過自己的強勢地位對部分風險進行額外的轉移,而當社會資本方居于強勢地位時,也會趁機將本應自身承擔的部分風險轉移給政府部門,將政府部門和社會資本方互相轉移的風險部分記為α,政府部門和社會資本方進行轉移風險的概率記為q,不通過強勢地位進行風險轉移的概率為1-q。
(3) 談判耗損系數。在每一回合討價還價的談判中會產生成本消耗,其中包括顯性成本和隱性成本,雙方談判的次數越多,負擔的成本就會越大[11]。在實際PPP項目中政府部門和社會資本方因為信息的不對稱和時間成本的差異,雙方談判各自的耗損系數也不同,在實際項目中,政府部門的談判支出要比社會資本方的談判支出小。因此,分別用δ1和δ2表示政府部門和社會資本方的談判耗損系數。
2.3 模型建立
2.3.1政府部門居于強勢地位
第一回合。政府部門首先出價,政府部門提出自己將承擔的風險為Z1和社會資本方將承擔的風險為1-Z1,另外,政府部門有q的概率會利用自身的強勢地位將本應自己承擔的風險進行部分轉移,進行轉移的風險部分為α,此時政府部門和社會資本方承擔的項目風險為:F11=q(Z1-α1),N11=q(1-Z1+α1)。而當政府部門以1-q的概率不利用強勢地位優勢將風險轉移給社會資本方時,政府部門與社會資本方承擔的風險為:F12=(1-q)Z1,N12=(1-q)(1-Z1)。因此在第一回合中,政府部門與社會資本方承擔風險的期望為:F1=F11+F12=q(Z1-α1)+(1-q)Z1,N1=N11+N12=q(1-Z1+α1)+(1-q)(1-Z1)。 在第一回合中,如果政府部門接受社會資本方的出價,則談判達成,至此結束,如果社會資本方拒絕政府部門的出價,則進入第二個回合。
第二個回合。此次由社會資本方先出價,提出政府部門需要承擔的風險部分為Z2,自身承擔的風險部分為1-Z2,政府部門仍然有q的概率利用自身強勢地位將風險轉移給社會資本方,轉移的風險部分為α2,談判的過程中發生一系列的成本,談判時間越長,成本就越高,因此,從第二個回合中加入政府部門和社會資本方的耗損系數δ1、δ2。則政府部門和社會資本方應承擔的風險為:F21=δ1q(Z2-α2),N21=δ2q(1-Z2+α2)。而當政府部門以1-q的概率不利于強勢地位將風險轉移給社會資本方時,政府部門與社會資本方承擔的風險為:F22=δ1(1-q)Z2,N22=δ2(1-q)(1-Z2)。得出在第二個回合中,政府部門與社會資本方承擔風險的期望分別為:F2=qδ1(Z2-α2)+δ1(1-q)Z2,N2=δ2q(1-Z2+α2)+δ2(1-q)(1-Z2)。
同理可得第三回合中,政府部門與社會資本方承擔風險的期望為:F3=qδ12(Z3-α3)+δ12Z3(1-q),N3=qδ22(1-Z3+α3)+(1-q)δ22(1-Z3)。第三回合中,如果政府部門接受了社會資本方的出價,則談判結束,如果政府部門拒絕社會資本方的出價,則進入下一個回合,雙方的博弈過程以此類推,直到有一方接受另一方的出價,對于風險分配的比例達成一致。
之后,對建立的模型進行求解。首先利用海薩尼轉換理論將不完全信息條件下的動態博弈轉換為完全但不完美條件下的動態博弈,在此需要明確的是對于無限回合的博弈,逆推點在第幾個回合不影響模型的結果[12-13]。選取第三回合作為逆推點,第二回合中社會資本方的出價如果使得政府部門承擔的風險期望值F2大于第三個回合的風險期望值F3,則政府部門會拒絕社會資本方的出價,進入第三個回合。因此,為了減少談判耗損成本,最優的策略應該為F2=F3,即qδ1(Z2-α2)+δ1(1-q)Z2=qδ12(Z3-α3)+δ12Z3(1-q),Z2=α2q+α1Z3-qδ1α3。
此時,社會資本方承擔的風險期望N2和N3為:N2=δ2q(1-Z2+α2)+δ2(1-q)(1-Z2+α2),N3=qδ22(1-Z3+α3)+(1-q)δ22(1-Z3)。
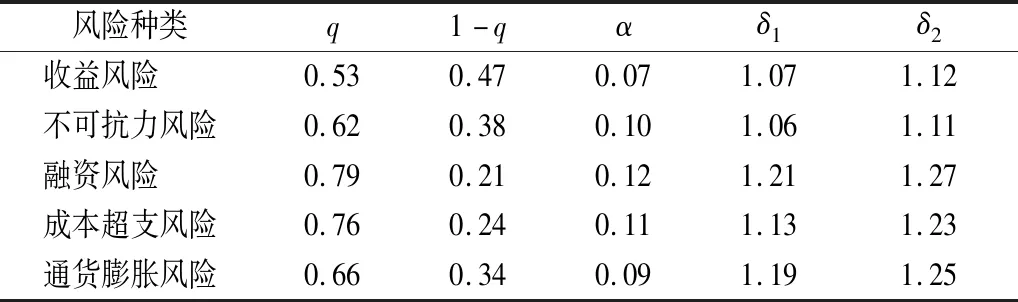
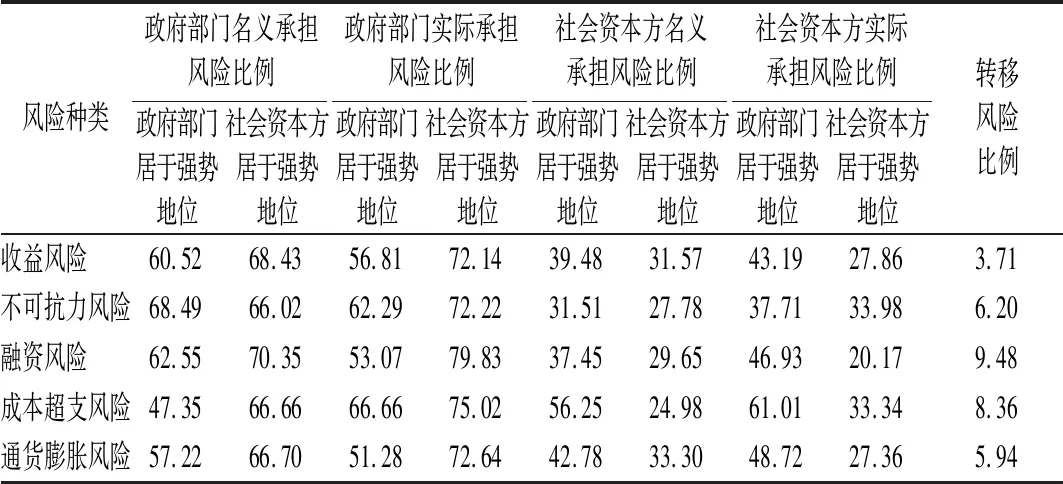
將兩者進行比較:N2-N3=δ2(1-Z2+α2-qδ2α3-δ2+δ2Z3),由1<δ1<δ2,0≤α3≤Z3≤1,0≤q≤1,可推導出N2 同理,現在回推到第一回合,如果N1>N2,社會資本方肯定拒絕政府部門的出價,進入下一回合,如果N1≤N2,為了不必要的談判耗損成本,最優的策略為:N1=N2。即q(1-Z1+α1)+(1-q)(1-Z1)=δ2(1-δ1Z3+qδ1α3),得出Z1=1+qα1-α2+δ1α2Z3-qα2δ2α3。 對一個無限回合的博弈過程來說,逆推點在第幾回合都不影響博弈的結果,所以:Z1=Z3。 由上式可得: (1) (2) 2.3.2社會資本方處于強勢地位 第一回合。社會資本方先出價,提出自己將承擔的風險部分為1-Z1和政府部門將承擔的風險部分為Z1,另外,社會資本方有q的概率會利用強勢地位將本應自己承擔的風險進行部分轉移,轉移的風險部分為α,此時雙方承擔的項目共擔風險為:N11=q(1-Z1-α1),F11=q(Z1+α1)。 而當社會資本方以1-q的概率不利用自身的強勢地位將風險轉移給政府部門時,政府部門與社會資本方承擔的風險為:N12=(1-q)(1-Z1),F12=(1-q)Z1。因此在第一回合中,政府部門與社會資本方承擔風險的期望值為:N1=N11+N12=q(1-Z1-α1)+(1-q)(1-Z1),F1=F11+F12=q(Z1+α1)+(1-q)Z1。 在第一回合中,如果政府部門接受社會資本方的出價,則談判達成,如果政府部門拒絕社會資本方的出價,則談判繼續進入第二個回合。 第二回合。由政府部門先出價,提出社會資本方應該承擔的風險為1-Z2,自身承擔的風險為Z2,政府部門仍然有q的概率利用強勢地位進行風險轉移,轉移的風險部分為α2,談判的過程中發生一系列的成本,談判時間越長,成本就越高,因此,從第二回合中加入公共部門和私人部門的耗損系數δ1、δ2。則政府部門和社會資本方應承擔的風險為:F21=qδ1(Z2+α2),N21=qδ2(1-Z2-α2)。 而當社會資本方以1-q的概率不利于強勢地位將風險轉移給政府部門時,政府部門與社會資本方承擔的風險為:F22=δ1(1-q)Z2,N22=δ2(1-q)(1-Z2)。 在第二回合中,政府部門與社會資本方承擔風險的期望為:F2=qδ1(Z2+α2)+δ1(1-q)Z2,N2=δ2q(1-Z2-α2)+δ2(1-q)(1-Z2) 同理可得,第三回合中,政府部門與社會資本方承擔風險的期望為:F3=qδ12(Z3+α3)+δ12Z3(1-q),N3=qδ22(1-Z3-α3)+(1-q)δ22(1-Z3) 在第三回合中,如果社會資本方接受政府部門的出價,則談判結束,如果社會資本方拒絕政府部門的出價,則進入下一個回合,雙方博弈過程以此類推,直到有一方接受另一方的出價,對于風險分配的比例達成一致。 結合海薩尼轉換理論,最終求解政府部門與社會資本方承擔的風險比例: (3) (4) 長春市城區地下綜合管廊項目是由中慶建設有限責任公司等10家社會資本方共同投資的PPP項目,其中社會資本認購80%股份,項目包括綜合管廊本體、附屬設施、控制中心和入廊管線,綜合管廊長度達23.85 km,合作期限30 a。 筆者采用德爾菲專家問卷調查法獲取相關博弈影響因子,向項目建設方、政府審批單位和咨詢單位等相關方發放了100份調查問卷,問卷內容包括:各類風險分擔的比例原則、談判過程中的談判成本損耗、各類風險的規避和轉移情況、本項目各類風險實際分擔情況。最后收回問卷91份,滿足本次調查使用。根據調查問卷數據分析,得到對應的參數δ1、δ2、α、q,如表1所列。 表1 長春市城區地下綜合管廊項目風險分配博弈影響因子Fig.1 Influencing factors of risk distribution of underground utility tunnel project in Changchun City 根據博弈模型以此例推,求出政府部門與社會資本方的風險分擔比例,具體結果列于表2。 表2 長春市城區地下綜合管廊項目風險分擔比例Fig.2 Risk sharing proportion of underground utility tunnel project in Changchun City % 本文構建了不完全信息條件下的動態PPP項目風險博弈模型,分析了政府部門和社會資本方分別在居于強勢地位時在談判中的風險分擔情形,得出雙方在進行談判時轉移風險的比例與概率與雙方地位差異、談判耗損系數有關。 (1) 雙方在談判時地位差異越大,進行額外風險轉移的概率也就越大;當政府部門將本應自己承擔的風險轉移給社會資本方后,社會資本方如果缺乏管控此類風險的能力,可能會導致項目的失敗,而PPP項目具有一定的公益性,項目失敗的最后承擔者是當地民眾。風險與收益是對等的,風險的轉移也意味著政府需要付出相對應的代價,這與采取PPP模式的初心不符。 (2) 當社會資本方將風險轉移給政府部門時,從表面看來,承擔項目風險是的當地政府,實際上最后承擔風險是納稅人或當地民眾,直接關系到當地民眾接受的服務質量,這依然與采取PPP模式的本意是相違背的,不利于PPP模式在我國的發展。 (3) 在PPP項目中,公私雙方的風險分擔比例與談判耗損系數具有相關關系,當政府部門處于強勢地位時,將部分風險進行轉移,社會資本方會花費大量的成本進行談判前的準備工作,在談判過程中會產生一定的談判成本。反之,當社會資本方處于強勢地位時,也會出現上述情況。 在PPP項目合作過程中,雙方需要在一個對等的基礎上來進行談判。首先,要確定風險分擔的基本原則,即最有能力控制該風險的一方來承擔,以此實現管理風險的成本最低,在風險管理過程中,也可將風險進行轉移給第三方來降低風險發生后的損失,如購買商業保險等方式。其次,PPP項目與群眾息息相關,項目的詳細信息應該及時公布,對于一些決策可以征求群眾的意見,確保群眾的知情權與參與權。再次,促進政府角色轉變,建立信用約束機制,提高信息透明度,PPP項目需要雙方在地位平等的基礎上來合作,政府部門的目的是借用社會資本來滿足公眾的需求,社會資本方的目的是獲得合理的回報,應該避免政府部門將風險轉移給社會資本方,更不能因為急于引入社會資本承擔更多的風險甚至做出收益“兜底”的承諾,否則最后損失的是公眾的利益。最后,在PPP項目合作過程中,公私雙方應該盡可能的去了解對方的信息和策略,避免信息不對稱產生的不必要的談判成本。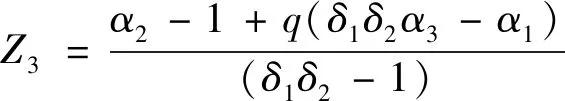
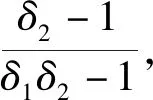
3 實證分析
4 結論及建議

