板材劇烈塑性變形擠壓模具設計及有限元分析

雷良煥

(中鐵建電氣化局集團南方工程有限公司，湖北武漢 430017)

1 ECAP 工藝原理

1981 年前蘇聯科學家Segal 等[1]提出ECAP 工藝的概念，試樣在通過ECAP 模具時受到一定程度的均勻純剪切擠壓應力，在試樣內部產生劇烈塑性變形，但一次完整加工后試樣的橫截面積不變，因此可反復加工達到細化晶粒提高材料性能的目的。通過ECAP 工藝加工出的塊狀材料晶粒可細化至1μm 以下，獲得超細晶粒材料（包括亞微米和納米材料），與其他制備工藝相比，ECAP 工藝流程簡單，生產成本低，且該工藝能獲得無殘留空隙的材料，在制備超細晶材料領域，ECAP 工藝有著巨大應用潛力。

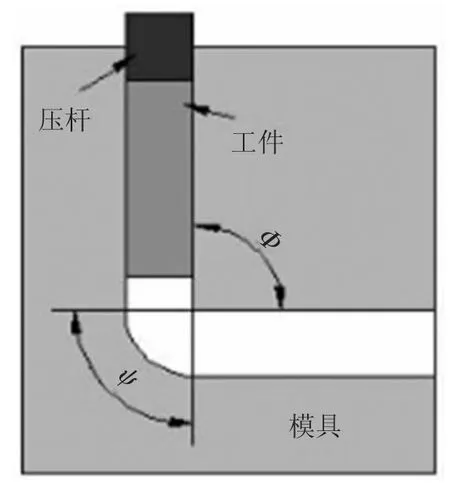
圖1 ECAP 原理示意圖

Segal[1-3]在摩擦m=0 和Ψ=0 的假設下，采用滑移線法分析了ECAP 工藝過程，并首次提出了單道次ECAP 累積等效應變εˉ和ECAP 擠壓力P 的計算公式：

式中，N 為擠壓道次；k 為剪切屈服應力；Φ為模具內角。

Iwahashi 等[4]在前蘇聯學者Segal 不考慮摩擦的基礎上，進一步做了關于模具外角ψ 對ECAP變形行為的影響的實驗，采用純剪切幾何變換法得出了以下更為通用的等效應變εˉ計算表達式：

從式2 可以看出，當外轉角ψ 一定時，累積的應變值隨內轉角Φ 的增大而減小；而當內轉角Φ一定時，累積的應變值隨著外轉角ψ 的減小而增大。隨著學者的大量研究也證實式3 可以比較準確預測ECAP 多道次應變累積值。

本文主要是在ECAP 工藝的基礎上，考慮到利用傳統ECAP 模具加工的材料樣式有限且加工效率較低的情況，提出了一種加工大尺寸鋁合金板材的ECAP 模具結構，并運用有限元分析技術，對模具內外角參數進行模擬，分析內外角對板材變形過程中的應變、載荷、應力的影響。

2 建立有限元模型

針對利用ECAP 工藝加工大面積板材的目的，設計一個雙通道ECAP 擠壓模具如圖2 所示，在fusion 360 建模軟件中建立二維模型，導入COMSOL Multiphysics 有限元分析軟件對其進行數值模擬，為了簡化計算量，僅模擬單邊加工過程。除待擠壓板材設置為塑性材料外，凹模和沖頭不考慮其受力和變形情況，均設定為剛性接觸體。材料的單元網格設置為默認的自由三角形網格，網格設置為極細化，物理擠壓步數設置為800 步，共擠壓150mm，由于是冷擠壓，所以擠壓溫度設置為常溫293.15K。COMSOL Multiphysics 軟件中大塑性應變的摩擦模型有兩種，庫倫摩擦模型和剪切摩擦模型[5]。庫倫摩擦模型通常用于正壓力不是很大、變形量又較小的塑性變形計算，ECAP 工藝金屬變形量很大，故應用剪切摩擦模型較為合適，其表達形式為：

式中，k 為變形金屬的剪切屈服應力；f 為摩擦因數，試樣與凹模內壁的摩擦力越小越好，故本文模擬取0.1。

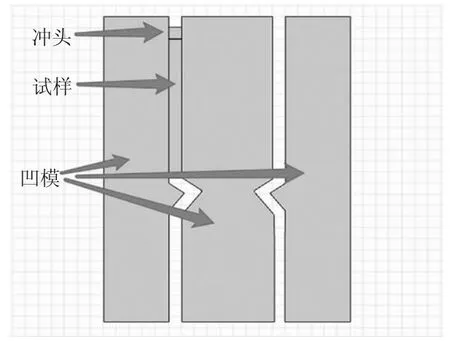
圖2 ECAP 模具的有限元模型圖

選用未經退火處理的1050 鋁合金板材作為擠壓材料。1050 鋁合金板材的密度為2.7g/cm3，彈性模量為69GPa，泊松比為0.33，其他材料屬性如表1 所示。

表1 材料尺寸和屬性

金屬材料的真實應力應變曲線是金屬塑性變形有限元模擬的重要參數之一，大變形條件下的金屬流動應力曲線需要借助特定的流動應力模型進行估計。

本次有限元模擬中使用的Ludwik 模型屬于“理想+硬化”模型[6]。因為在數學上“理想+硬化”模型更加符合金屬硬化的物理意義，更多工程研究人員偏向選用“理想+硬化”模型估測材料的大塑性變形流動應力曲線。Ludwik（又名Ludwig）模型是最早提出的“理想+硬化”非飽和模型，其公式為[7]：

式中，A 為強度系數（A＞0）；n 為硬化指數（n ＞0）。

將1050 鋁合金的相關參數帶入式5，得到如圖3 所示的流動應力曲線。

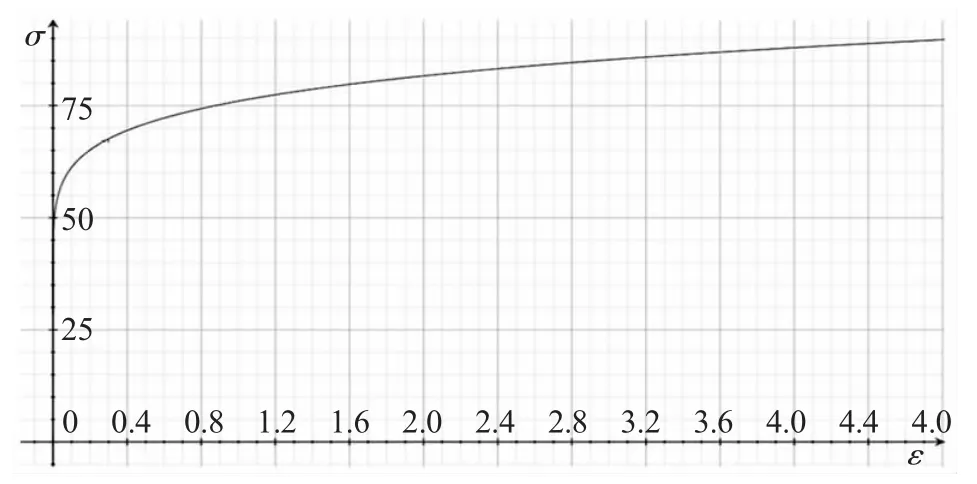
圖3 1050 鋁合金流動應力曲線

模具內外角參數的變化，使加工試樣內部變形區域所受的載荷、應變、應力和溫度都有所不同，想要得到微觀結構細小、力學性能良好的板材，需要使材料發生均勻的大應變變形，以有效塑性應變模擬數據分析，選取不同內外角結構參數進行比較，以得到較為理想的內外角結構參數。

3 ECAP 數值模擬結果分析

根據前人的試驗數據，在中間拐角處選取了三組內外角參數來比較分析。三組內外角及其擠壓結果分別如圖4a、b、c 所示。

圖4 不同內外轉角ECAP 變形后等效應變分布云圖

從圖中可看出，隨著模具中間轉角處的內外角角度的增加，試樣經三個轉角剪切變形后，其有效塑性應變最大值依次遞減，試樣的平均有效應變值大約為有效應變最大值的一半。圖4a 中平均有效應變值約為3.32，再經一次重復擠壓加工后即可達到ECAP 工藝的要求。而圖4b、c 中平均有效應變約為2.2，再經兩次重復擠壓加工后方可達到ECAP 工藝要求。從應變均勻性角度來看，圖3a中應變最大值分布在試樣截面較集中的一部分區域，較大區域的有效應變值相對均勻，圖4b、c 中試樣截面的有效應變值梯度較大，分布較不均勻。綜上，第一組內外角角度是比較理想的模具結構參數。

3.1 等效應力和有效塑性應變分布

圖5 為材料在內角Φ=90°，外角ψ=10.4°的凹模內擠壓過程中的等效應力和有效塑性應變分布圖，可以看到在圖5a 中，試樣經過第一道拐角時，其在轉角塑性變形區的等效應力分布差別不大，試樣的應力極值出現在剪切變形區的轉角及其下部，等效應力的極大值達到74.3MPa，由圖5b、d可以看出，試樣經過每一道轉角后，其最大應力值均出現在最后一道轉角及其下部，而在試樣兩端，等效應力值逐漸減小。試樣經三道轉角的剪切變形和擠壓后，試樣的厚度減小較多，第三道轉角之前的通道被填滿，等效應力在第二道轉角下部靠模具內側較集中。

由圖5a 可看出，當試樣經過第一道轉角時，試樣已變形區有效塑性應變分布較均勻，其應變最大值達到0.77。試樣經第二道轉角和第三道轉角擠壓和剪切變形后，試樣緊貼模具內側部分的有效塑性應變較大，在第二次重復擠壓過程中，應考慮將板材旋轉180°擠壓，盡量避免板材表面出現裂紋的情況。另外可以看出試樣應力應變集中在轉角處且相當大，這對模具的磨損影響很大，應該盡量減小試樣和模具內壁的摩擦，這對后期模具結構的改進有很大的幫助。

圖5 材料等效應力和有效塑性應變分布云圖

3.2 沖頭載荷-位移曲線圖

圖6 為ECAP 模具沖頭的載荷-位移曲線圖，大致可以看出，該圖中有三個上升期和兩個穩定期。三個上升期分別為板材通過三處轉角時，沖頭載荷隨著板材向下的位移增大而增大；兩個穩定期分別為板材通過第一道轉角還未經過第二道轉角和通過第三道轉角之后；而當板材通過第二道轉角后沖頭載荷上升的趨勢有所下降。

板材通過第一道轉角后，在第二道轉角處逐漸充滿變形區，擠壓材料在通道拐角底部時，出現了金屬滯留區（即死區），位于滯留區內的金屬流速比其他區域的金屬流速慢，導致沖頭載荷隨著滯留區內金屬的不斷堆積而急劇上升。

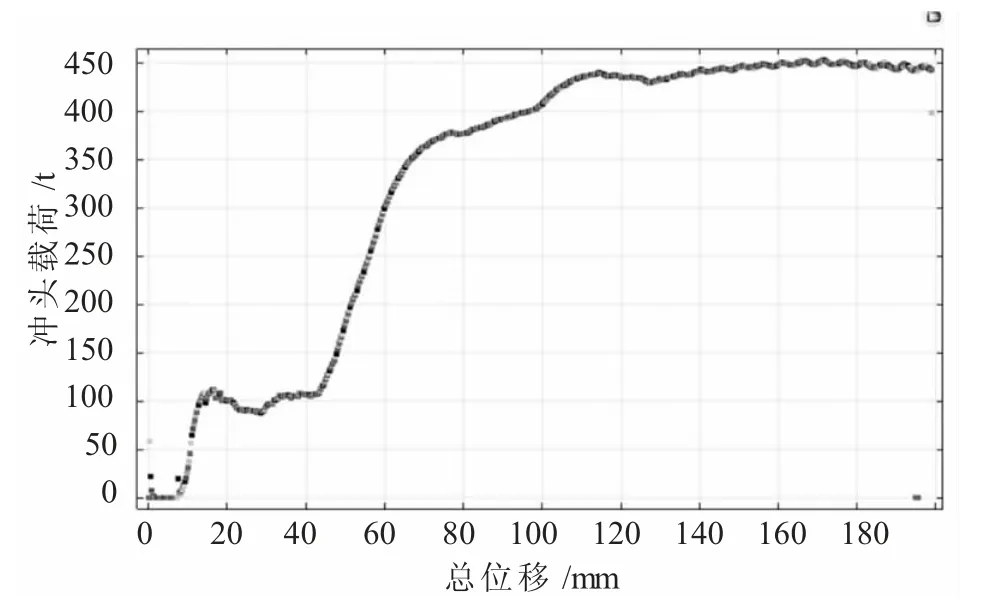
圖6 沖頭載荷-位移曲線圖

4 結論

本文提出了一種滿足大尺寸鋁合金板材ECAP 加工的模具結構，并利用COMSOL Multiphysics 有限元分析軟件模擬分析了模具中間拐角處三組不同的內外角參數對試樣應力應變的影響，得出了以下結論：

（1）隨著模具中間拐角處的內外角角度的增加，試樣經三個拐角剪切變形后，其有效塑性應變值依次遞減。

（2）基于COMSOL Multiphysics 有限元軟件，主要分析了不同模具結構參數下擠壓力和有效塑性應變的變化規律，探究了相關因素對變形金屬成形均勻性和真應變的影響，最終確定了中間拐角處內角Φ=90°，外角ψ=10.4°的模具結構，使試樣產生了最大的應變值。

（3）試樣在通過模具拐角處受到的擠壓應力最大，應盡可能減小試樣和模具之間的摩擦力，降低模具磨損。

（4）該模具只需要兩遍重復加工就能滿足ECAP 工藝要求，兩次加工之間應將板材翻轉180°，避免板材表面出現裂紋，且可以兩組板材同時加工，提高效率。