有限導電內核的驅動方式對發(fā)電機模型的影響

丁嘉威， 王正濤,2*， 詹文臻， 劉美琴

1 武漢大學測繪學院， 武漢 430079 2 武漢大學地球空間環(huán)境與大地測量教育部重點實驗室， 武漢 430079

0 引言

行星的磁流體內核的流體動力學模擬主要是通過求解包括科里奧利力在內的Navier-Stokes方程，并結合Boussinesq近似下的磁流體動力學(MHD)感應方程、溫度(或熵)方程與化學成分(本文未考慮)方程來實現的，得益于數值算法的不斷改進以及高性能計算機的發(fā)展，使得當前發(fā)電機模型的數值模擬計算速度越來越快，描述各物理量的參數越來越多且日益接近真實值.

1995年，超級計算機Cray C90上成功模擬了一個包含有限導電內核的三維自恰地球發(fā)電機模型(Glatzmaier and Roberts, 1995a)，同年又模擬了長達4萬年的地球磁場，并成功實現了磁場的翻轉(Glatzmaier and Roberts, 1995b).此后相關研究者們在以上基礎上對發(fā)電機模型中的物理參數進行修改或增加、或使用更為合理的物理參數及數值方法來得到新的發(fā)電機模型并進行系統(tǒng)性的研究(Christensen et al., 1998; Christensen et al., 1999; Olson et al., 1999; Christensen et al., 2001; Kutzner and Christensen, 2002; Takahashi et al., 2007; Takahashi et al., 2008; Wicht, 2014; Matsui et al., 2016).地球內核的超速旋轉現象的發(fā)現(Song and Richards, 1996)，利用地震得到的地球內核表面的鑲嵌結構(Krasnoshchekov et al., 2005)，地核條件下鐵、固態(tài)鐵和鐵硅混合物的導熱性和導電性(Pozzo et al., 2012, 2014)，利用高壓試驗和三維x射線顯微層析成像技術推斷的核-幔邊界處的溫度數據(Nomura et al., 2014)，通過數值模擬分析得到的深內部地球結構對內核平動振蕩本征周期的影響(江穎等, 2014)，關于核幔耦合對地球自由核章動的激發(fā)影響(崔小明等, 2018)等各類更精細的地球內部數據或相關研究都為更真實的地球(磁流體)發(fā)電機模型提供了很好的數據條件.

對于內核在發(fā)電機中的作用，Hollerbach和Jones(1993)關于內核對地磁場波動和翻轉的作用進行了研究；Glatzmaier 和Roberts(1995b)提出了包含有限導電內核的三維、自恰地球發(fā)電機模型，并成功實現了主磁場的翻轉；Wicht(2002)研究分析了有限導電內核對地磁場翻轉頻率的影響，并詳細描述了引入內核后的發(fā)電機方程；Reshetnyak(2016)研究了半徑不斷增大的內核在發(fā)電機中的作用.而關于內核在外核驅動下的高轉速(通常每時間尺度達幾百弧度)、大波動的問題，可以通過引入引力耦合來穩(wěn)定內核的轉速(Aubert and Dumberry, 2011).需要注意的是此處的高轉速、大波動是以慣性系為參考進行描述的，而并非以外核系統(tǒng)作為參考.

本文以Takahashi等(2007, 2008)所提出的兩種數值發(fā)電機模型為基準，研究有限導電內核在兩種旋轉方式下對發(fā)電機模型的極向和環(huán)向動能、極向和環(huán)向磁能、核-幔邊界處的磁場強度、磁雷諾數、磁極翻轉頻率、軸向偶極子強度、赤道對稱性、緯向性和磁通量集中度的影響，其中后四者用于研究類地發(fā)電機的成立條件時所用的四種參數(Christensen et al., 2010).

1 基本原理

通常，對于磁流體發(fā)電機模型的求解會從描述流體運動的Navier-Stokes方程出發(fā)：

(1)

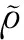
最終得到其無量綱形式為：

(2)

其中p″為修正后的壓力項，ez為旋轉軸方向的單位矢量.無量綱參數的具體表達式分別為：

埃克曼數

(3)

瑞利數

(4)

普朗特數

(5)

磁普朗特數

(6)

式中，下標“o”表示外核邊界處的相應物理值，“i”表示內核邊界處的相應物理值，d為外核厚度，ΔT為內外核溫度差，κ為熱擴散率.

最后，將方程(2)與以下方程聯(lián)立：

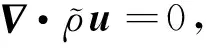
(7)

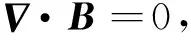
(8)

(9)

(10)

即得到求解發(fā)電機模型的無量綱方程組.

將有限導電的內核引入發(fā)電機模型后，內核和外核的發(fā)電機方程就必須同時進行求解，它們由磁場和水平電場的連續(xù)性來關聯(lián)：

B=Bi,r=ri;

EH=EHi,r=ri.

(11)

若內核在外核的驅動下發(fā)生轉動，則其驅動力包含洛倫茲力與黏性力.轉速可由角動量方程進行描述，其具體表達式為：

(12)

其中I是沿Z軸旋轉的內核轉動慣量，ωi為內核旋轉角速度，ΓL、Γv分別對應于洛倫茲力及黏性力.內核為導電的情況下，其對應的發(fā)電機方程為：

(13)

在以上基礎上通過更改地球內核的電導率、旋轉方式來研究其對主磁場帶來的影響.

2 模型參數

2.1 基準模型

本文選擇使用了Takahashi等(2007)用于研究磁極轉換所使用的模型及Takahashi等(2008)所提出的數值發(fā)電機中埃克曼數為2×10-5的模型作為基準模型，分別簡稱為FT07和FT08，模型中的球諧展開階次為16階，徑向的切比雪夫多項式的展開項數為32，時間尺度方案選擇了黏性擴散時間，其具體轉換方法即前文對時間t的變量代換.

模型FT07所對應的物理參數為：E=1×10-5，Ra=8×107，Pm=0.5，Pr=1；模型FT08所對應的物理參數為：E=2×10-5，Ra=2×107，Pm=1.5，Pr=1.

對于內核電導率，基準模型將其設定為絕緣，且與外核之間不存在任何相關物理作用的.

本文默認所有內核的密度均等于外核密度.

所有模型所對應的內核的機械邊界條件選擇使用剛性、不可穿透的邊界，這與真實的內核-外核邊界物理上最為接近.

內核的熱邊界條件默認均為固定熵條件，即熵si=sbottom.

2.2 由外核驅動旋轉的有限導電內核模型(DOC, Driven by Outer Core)

包含有限導電內核的模型的無量綱參數、內核密度、內核的機械邊界條件以及熱邊界條件均與進行比對的相應基準模型保持一致，且內核的電導率均認為與外核相同(目前內核的增長通常被認為是外核物質在內核邊界上凝固的結果，因此認為內核電導率和外核電導率相同在物理上解釋可能更為合理).

此模型下，內核旋轉被認為是洛倫茲力和黏滯力共同作用下的結果.

2.3 固定旋轉速度的有限導電內核的模型I(FSR I, Fixed Super Rotation I)

該模型的轉速使用對應的DOC模型在相應時間尺度內的最大轉速.分別對應于351.06rad/時間尺度和383.96rad/時間尺度.

需要注意的是，此模型下的內核不會與外核存在任何有關力的作用，即認為內核是自發(fā)旋轉、不受外核影響的.

2.4 固定旋轉速度的有限導電內核的模型II(FSR II, Fixed Super Rotation II)

此模型與FSR I的區(qū)別僅在于內核的轉速不同，所使用的轉速為所對應的DOC模型在對應時間尺度下的內核平均轉速，分別為：32.90rad/時間尺度和-22.68rad/時間尺度.

2.5 固定旋轉速度的有限導電內核的模型III(FSR III, Fixed Super Rotation III)

與FSR II類似，其轉速對應為：-296.69rad/時間尺度和-363.98rad/時間尺度.

3 模型間的比較分析

3.1 核-幔邊界處的磁場強度

核-幔邊界處的磁場強度通常使用埃爾澤塞爾數進行描述：

(14)

其大小等于無量綱磁場強度的平方，該數也可以用于描述洛倫茲力與科里奧利力的比值.式中下標rms表均方根.

根據圖1可以看出模型FT07及其對應的幾種比對模型的磁場強度在0.4個時間尺度后基本在0.3左右上下波動，因此對于模型FT07，其所有的對比均使用0.4～3個時間尺度內的數據.同理根據圖2，FT08使用0.5～3個時間尺度內的數據.

圖1 模型FT07及其對應的DOC、FSR I、FSR II、FSR III的核-幔邊界處的磁場強度.該模型所使用的積分時間步長的數量級達10-6，造成了原圖曲線存在大量重疊的情況，因此此處每隔5000個點取一個來繪制其趨勢，計算時仍采用全部數據.后作類似處理的圖像會標注相應的間隔，如“(5000)”Fig.1 Magnetic field intensity at core-mantle boundary of benchmark dynamo FT07 and its corresponding dynamo DOC, FSR I, FSR II, and FSR III. Order of magnitude of integral time step used in this model is up to 10-6, which causes a large amount of overlap in the original graph curve. Therefore, here every 5000 points are taken to plot its trend, but all data are still used in the calculation. Images processed similarly are marked with corresponding intervals, for example,“(5000)”

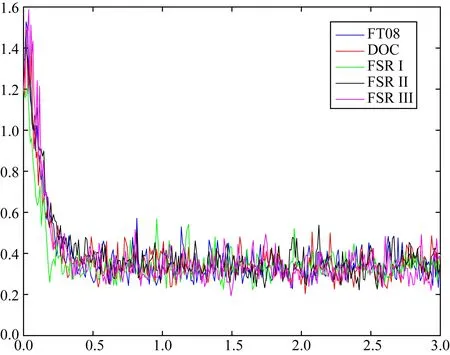
圖2 模型FT08及其對應的DOC、FSR I、FSR II、FSR III的核-幔邊界處的磁場強度(5000)Fig.2 Magnetic field intensity at core-mantle boundary of benchmark dynamo FT08 and its corresponding dynamo DOC, FSR I, FSR II, and FSR III (5000)

3.2 DOC模型轉速

內核轉速可由角動量方程(12)進行描述.計算得到的轉速圖見圖3—4.

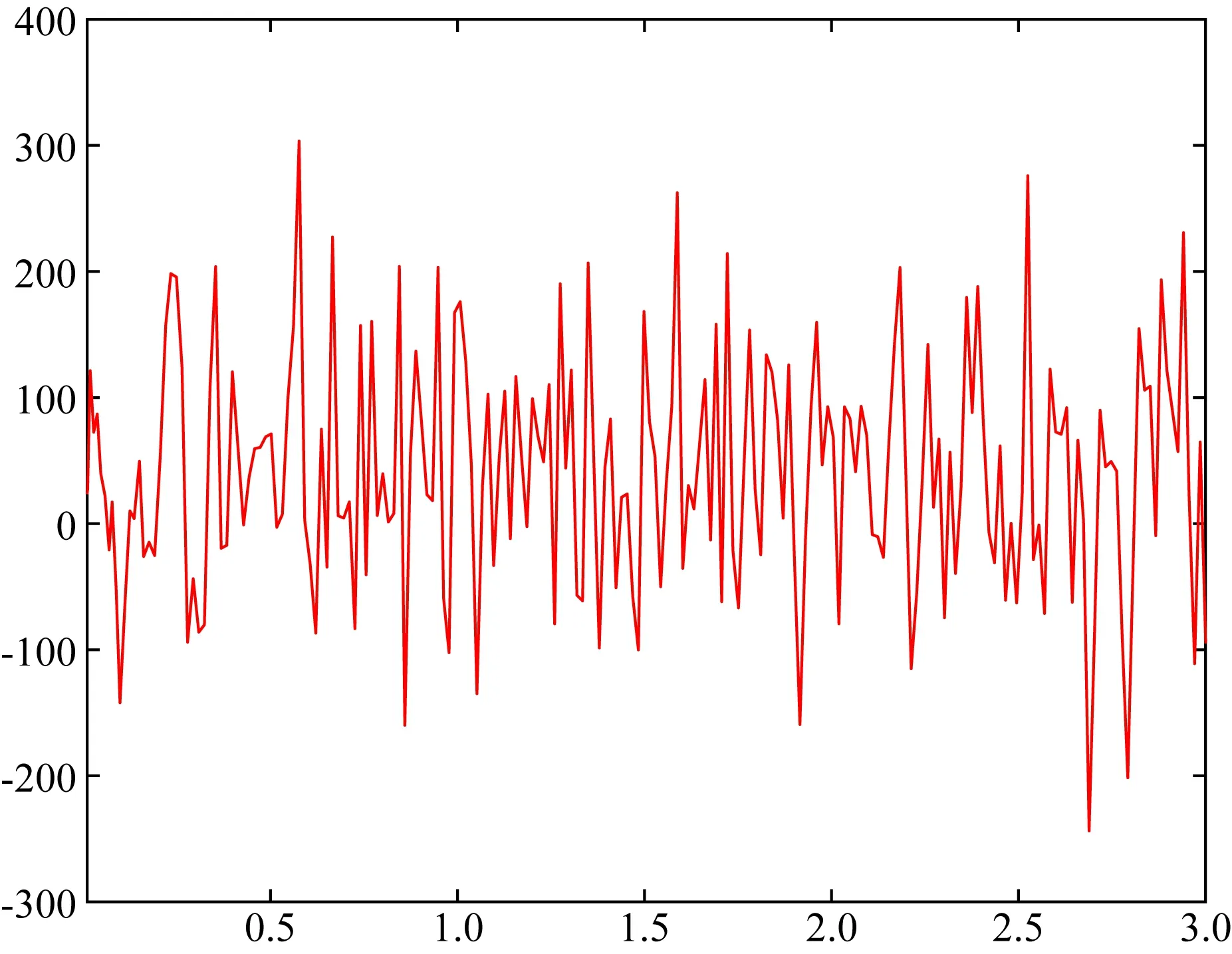
圖3 模型FT07所對應的DOC模型在0.01～3個時間尺度內的內核轉速(5000)Fig.3 Inner-core rotation speed of the DOC model corresponding to model FT07 in 0.01～3 timescales (5000)

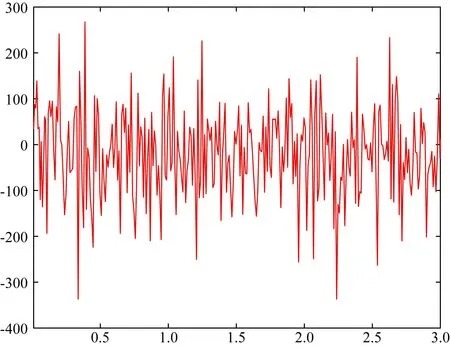
圖4 模型FT08所對應的DOC模型在0.01～3個時間尺度內的內核轉速(5000)Fig.4 Inner-core rotation speed of the DOC model corresponding to model FT08 in 0.01～3 timescales (5000)

3.3 外核能量

通過比較外核的動能、磁能以及相應的磁場變化來研究不同驅動方式下的內核對數值發(fā)電機作用的影響.在螺線向量場在球坐標系下的分析中通常會對其應用極向-環(huán)向分解，是亥姆霍茲分解的一個受限制的形式，在本文所涉及的問題中，動能和磁能具體的極向-環(huán)向分解后表達形式分別為：

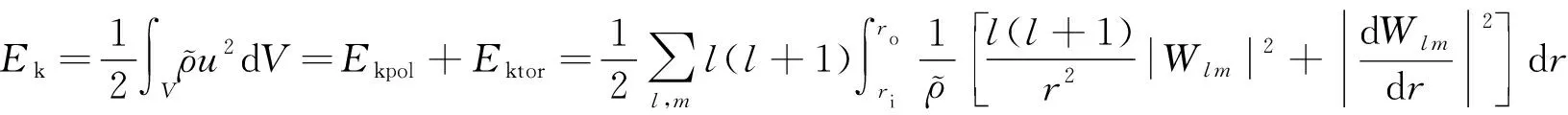
(15)

(16)

式中，Wl m為動力場極向位能，Zl m為動力場環(huán)向位能，bl m為磁場極向位能，jl m為磁場環(huán)向位能.

3.4 磁雷諾數

磁雷諾數的定義為：

(17)

主要用于描述磁流體內部速度u和磁場B的方均根值的比值.

3.5 磁極翻轉頻率

磁極翻轉頻率f可根據磁極緯度的變化次數統(tǒng)計得到.

3.6 軸向偶極子強度

本文中軸向偶極子強度定義為偶極子(axial dipole,AD)與非偶極子(non-axial dipole,NAD)之比：

(18)

3.7 赤道對稱性

對于赤道對稱性，通常使用奇偶比O/E進行描述，即2到8階的調和級數在核-幔邊界處的階次和(n+m)為奇數的分量和與階次和為偶數的分量和之比.

3.8 緯向性

緯向性即緯向-非緯向比Z/NZ是核-幔邊界處所有緯向性分量和非緯向性分量之比.

3.9 磁通量集中度

核-幔邊界處的磁通量在一定程度上集中并形成了強輻向場斑塊Br，可用通量集中因子FCF來定量描述：

(19)

其中〈〉表示在整個球面上求平均.

3.10 比較分析

表1給出了包含導電內核的各發(fā)電機模型的各物理量較基準模型的變化量.可以看出，有限導電內核的引入對模型的磁場強度只會產生最高不到4%的變化，極、環(huán)向動能最高僅約2%，極、環(huán)向磁能最高也約為4%，磁雷諾數的變化量不到1%，磁通量強度最高約5%.但對于軸向偶極子強度和磁極翻轉頻率，各模型相較基準模型的變化量則存在較大差異，特別的，DOC模型對于磁極翻轉頻率幾乎沒有影響；對于赤道對稱性，除以FT07為基準的FSR I的變化量達到+19.03%之外，其他的變化量均小于6%；在緯向性的比較中，除了以FT07為基準的FSR II和FSR III的變化量達17%以上，其他模型的變化量均在10%以下.

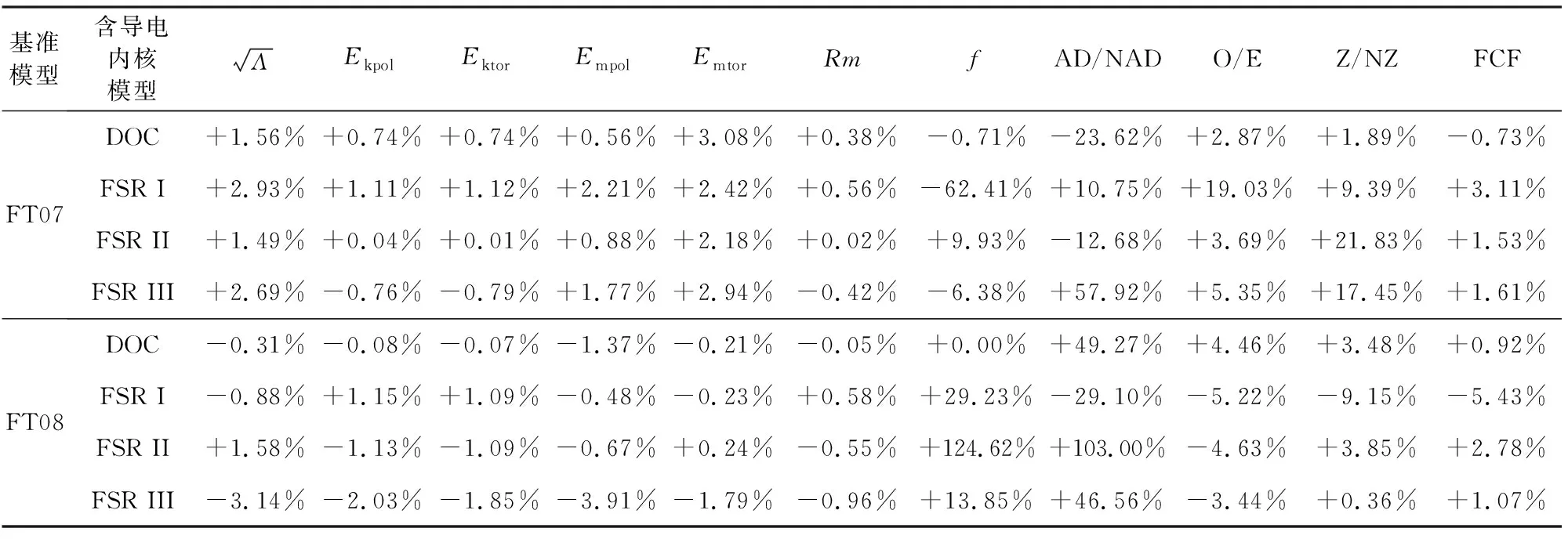
表1 各模型對應的各物理量較基準模型的變化量Table 1 Variation of each physical quantity corresponding to each model compared with the benchmark dynamo

4 結論

有限導電內核的引入，對于模型的磁場強度、極向和環(huán)向動能、極向和環(huán)向磁能、磁雷諾數和磁通量集中度的影響是極弱的，只會產生小于6%的變化量.這可能是由于內核本身的能量相對于外核來說是極小的，因此引入有限導電的內核后，其所帶來的影響也應不會明顯.

圖5 模型FT07及其對應的DOC、FSR I、FSR II、FSR III的磁極緯度Fig.5 Latitude of magnetic pole of benchmark dynamo FT07 and its corresponding dynamo DOC, FSR I, FSR II, and FSR III (5000)

對于軸向偶極子強度，由于本文所使用的模型是可以實現磁場翻轉的發(fā)電機模型，而這類模型的軸向偶極子強度通常都較弱，其本身基數較小，因此引入有限導電內核后，導致其相對變化量較大，但其最大絕對變化量小于0.03，且結合圖5—8，可以明顯看出，有限導電內核對軸向偶極子強度的影響更多的集中在磁極翻轉的時刻，這表明對于那些偶極性較弱的發(fā)電機模型，有限導電內核的引入與否會直接影響該發(fā)電機的偶極子強度，并且對于可實現磁場翻轉的發(fā)電機模型來說，這一影響可能會更明顯.

而對于赤道對稱性和緯向性，除部分模型存在較大的變化外，其余模型的影響均小于10%，若發(fā)電機模型涉及以上兩個物理量，有限導電內核(FSR)仍是值得考慮的因素.

對于翻轉頻率來說，DOC模型的翻轉次數與基準模型幾乎完全一致，而FSR模型則對翻轉頻率造成了不同程度的較明顯的影響.這表明DOC模型的內核旋轉雖然波動大、轉速高，但可能由于其驅動

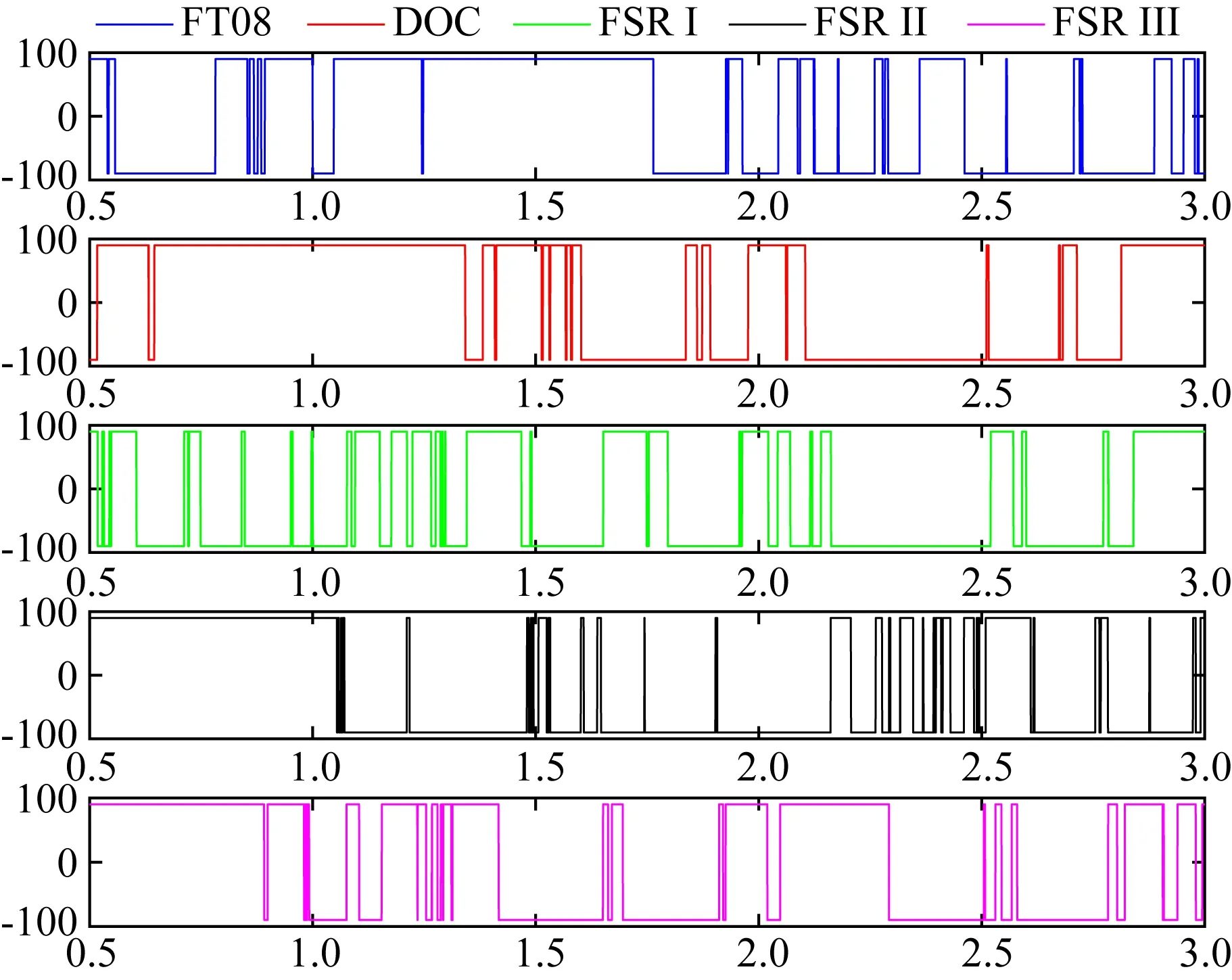
圖6 模型FT08及其對應的DOC、FSR I、FSR II、FSR III的磁極緯度Fig.6 Latitude of magnetic pole of benchmark dynamo FT08 and its corresponding dynamo DOC, FSR I, FSR II, and FSR III (5000)

圖7 模型FT07及其對應的DOC、FSR I、FSR II、FSR III的軸向偶極子強度(5000)Fig.7 Relative axial dipole power of benchmark dynamo FT07 and its corresponding dynamo DOC, FSR I, FSR II, and FSR III (5000)

圖8 模型FT08及其對應的DOC、FSR I、FSR II、FSR III的軸向偶極子強度(5000)Fig.8 Relative axial dipole power of benchmark dynamo FT08 and its corresponding dynamo DOC, FSR I, FSR II, and FSR III (5000)

方式及機理與真實情況相近且考慮到內核本身的能量對外核產生的影響程度有限，因此DOC模型與基準模型的翻轉頻率幾乎完全一致也在物理上更為合理；而對于FSR模型，其本身就是一種為了方便控制轉速而理想化后的模型，因此其內核可能會對外核磁流體產生一定影響，而引起磁極翻轉頻率發(fā)生較明顯變化.

總體來說，本文中的DOC模型除偶極性以外，對于其他物理量所能帶來的變化都是可忽略的，且考慮到實際內核較外核的能量比來說，以上結果是較合理的.

致謝MagIC開發(fā)團隊提供的球殼中的流體動力學數值代碼MagIC、南方科技大學林玉峰副教授提供的理論指導及武漢大學超算中心提供的算力支持.