某重型履帶裝甲車輛機械-液力聯合制動建模與仿真分析

陳長鑫， 羅 雷， 周 凱， 房 遠

（1.武警工程大學 a.研究生大隊，b.裝備管理與保障學院， 陜西 西安 710086； 2.中國人民解放軍32272部隊， 甘肅 蘭州 730000； 3.陸軍裝甲兵學院兵器與控制系， 北京 100072）

引言

制動系統是履帶裝甲車輛不可或缺的重要組成部分[1]，是保持戰場生存能力，提高裝備機動性突擊力的前提和保證[2]。現階段各重型履帶裝甲車輛在高速行駛時均以液力制動作為主要制動方式，其他工況一般采用機械-液力聯合制動[3-4]。建立履帶裝甲車輛動力學模型和制動系統數學模型并進行聯合制動仿真，是評估和驗證制動系統性能的有效手段[5-6]。因此，在參數匹配計算的基礎上，針對性地建立了某重型履帶裝甲車輛動力學模型，構建了符合實際工況的機械-液力聯合制動系統模型，并對聯合制動系統進行仿真和結果分析，驗證了模型和仿真的科學性正確性。

1 履帶裝甲車輛動力學建模

給出某重型履帶裝甲車輛的參數匹配計算過程，采用RecurDyn 軟件建立車輛動力學模型和路面模型。

1.1 參數匹配計算

某重型履帶裝甲車輛重量m=52 t，車體（車尖至車尾）長L0=7.5 m，炮向前（帶備用油箱）車長L1=11.3 m，車寬（不帶側屏蔽）H0=3.4 m，車高（至炮塔頂）H1=2.3 m，車底距地高（距車底平面）H2=0.5 m，履帶中心距B=2.8 m，履帶著地長L=5 m，主動輪節圓半徑r=0.318 m。

車輛行駛阻力計算如下：

1）空氣阻力：若v 以km/h 為單位，則空氣阻力Fw可按下式估算：

式中：CD為空氣阻力系數，主要取決于履帶裝甲車輛車體形狀，一般取值1.2～1.6，此處取值1.4；A 為履帶裝甲車輛迎風面積，一般取值6～8 m2，此處取值7 m2。若最大車速v=85 km/h，則最大車速時空氣阻力Fw=3 293.3 N。

2）滾動阻力：車輛在水平硬路面上的滾動阻力Ff為：

式中：f 為滾動阻力系數，考慮到車重50 t 以上且負重輪帶橡膠輪緣，滾動阻力系數取值0.04；G 為車重，按 G=mg 計算，g 取值 9.8 m/s2。

其他阻力或因素，因影響很小或仿真中不涉及可忽略不計。例如，履帶裝甲車輛車首阻力，因仿真過程中地面為堅硬混凝土路面，車輛不存在下陷問題，故無須克服車首阻力。

1.2 整車動力學建模

履帶裝甲車輛在水平堅硬路面上實施制動，其制動受力分析如下頁圖1 所示。其動力學平衡方程為：

式中：FB是堅硬路面通過制動器施加給履帶裝甲車輛的制動力，最大值FBmax=φG，其中，φ 為履帶附著系數，是一個綜合性參數。φ 值的主要影響因素是地面性質，重要影響因素是車輛結構，特別是履帶板結構；此外，車輛行駛速度v 對φ 值也有一定影響。以鋼制履帶裝甲車輛為例，在混凝土路面行駛時，φ 取值 0.7 左右；在砂石路面行駛時，φ 取值 0.6～0.7；在黏土路面行駛時，φ 取值0.4 左右。

某重型履帶裝甲車輛通過RecurDyn 軟件建立的動力學模型如下頁圖2 所示，建模的過程中應用了履帶包Track_HM。

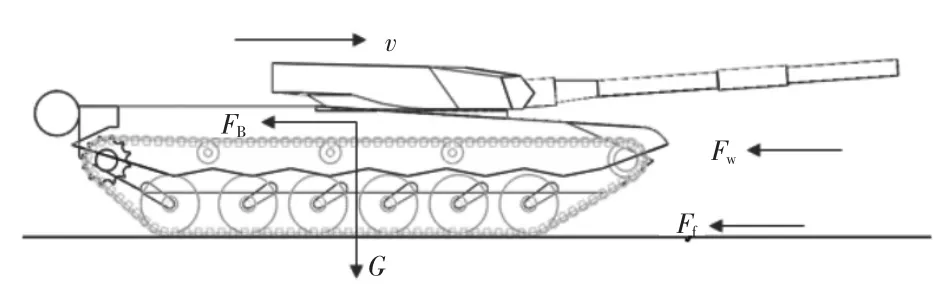
圖1 某重型履帶裝甲車輛制動受力分析圖

圖2 某重型履帶裝甲車輛的動力學模型

在RecurDyn 模型中，應用約束中的常用鉸和外力載荷中的直接外力，對坦克懸掛系統進行表示和仿真。應用轉動副加轉動軸向力表示扭力軸，建立6個平衡肘，用轉動副和固定副的組合連接負重輪。液壓減振器是懸掛裝置的阻尼元件，液壓緩沖器是懸掛裝置中的輔助緩沖和負重輪（平衡肘）行程限位元件。履帶裝甲車輛在堅硬平坦路面上制動，液壓減振器和液壓緩沖器發揮效果不明顯，故在模型中省略。平衡肘與負重輪的連接處，可忽略摩擦力。

1.3 RecurDyn 中的路面參數設置

在RecurDyn 軟件中，路面之間的接觸屬于剛柔混合系統仿真中的FFlex 接觸。在Track_HM 履帶包中，履帶與地面的接觸和作用已經由RecurDyn 軟件預先設置并打包。

對于堅硬路面（瀝青、混凝土等）的仿真，認為相互接觸的履帶和路面都是剛體，二者之間的作用力表現為摩擦力。法向接觸力fn的計算公式為：

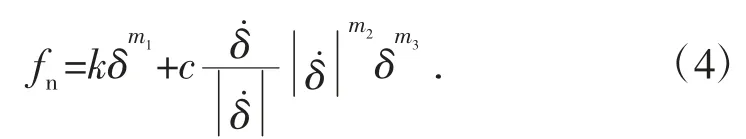
式中：k 為接觸剛度；c 為阻尼系數；δ 為接觸穿透深度；為其對于時間的導數（接觸點的相對速度）；m1為剛度指數；m2為阻尼系數，二者產生非線性接觸力；m3為缺口指數，產生缺口阻尼效應，當穿刺很小時，由于負阻尼力的作用，法向接觸力可能為負，可以設m3＞1 來克服（默認情況下為0）。

摩擦力的計算方程為：

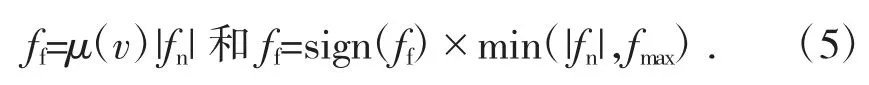
式中：fmax為最大摩擦力；μ（v）為摩擦系數，取決于靜態門檻速度、動態門檻速度、靜摩擦系數等，與相對速度相關，依據RecurDyn 中的半正矢階躍函數havsin 確定。堅硬路面參數設置如圖3 所示。

2 聯合仿真模型建模

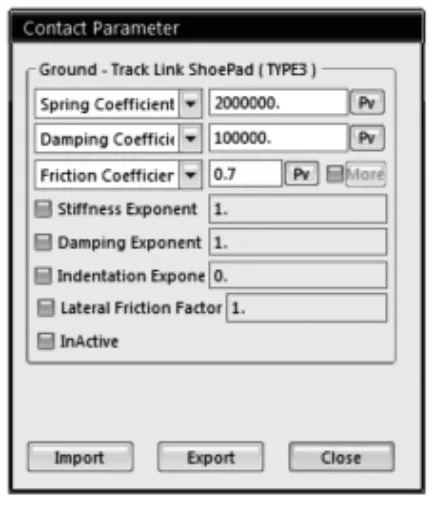
圖3 路面參數設置

建立液力緩速器的輸出外特性的數學模型，采用Matlab/Simulink 軟件建立聯合仿真模型。

2.1 機械-液力聯合制動系統建模

依據文獻[7]進行液力緩速器建模。文獻[7]分析了第三代主戰坦克的傳動系統與液力變矩-減速器的相互作用，給出了液力變矩-減速器的詳細數學模型，包括制動力距公式、工作油流量公式、散熱器的散熱能力計算、制動過程工作油的升溫計算等。對文獻[7]中的液力緩速器的輸出外特性曲線進行擬合，得出液力緩速器的數學模型。

機械制動器建模采用常量值輸出形式。如果考慮側減速器和側變速箱的傳動比，機械制動器的理論輸出最大能達到100 kN·m[7]。這將使重50 t、制動初速度65 km/h 的履帶裝甲車輛在2 s 內停車，但這在現實中是不可能的，也沒有仿真的意義。因此，機械制動器模型輸出常量值必須符合實際，在此，使用能使制動系統方案中的履帶裝甲車輛模型保持穩定的最大力矩作為輸出常量值。

2.2 Matlab/Simulink 聯合仿真建模

建立某重型履帶裝甲車輛的機械-液力制動聯合仿真模型如圖4 所示。聯合仿真模型的輸出變量為履帶裝甲車輛的速度、加速度、位移、偏移、兩側主動輪的轉動角速度。模型的輸入變量為制動或加速扭矩，作用在兩側主動輪上。

2.3 聯合制動系統的控制策略

根據文獻[8]和文獻[9]中對履帶裝甲車輛制動試驗的規定，參考文獻[7]的內容，作出以下設定：制動初速度不能過高；不能采用機械制動器進行高速制動。

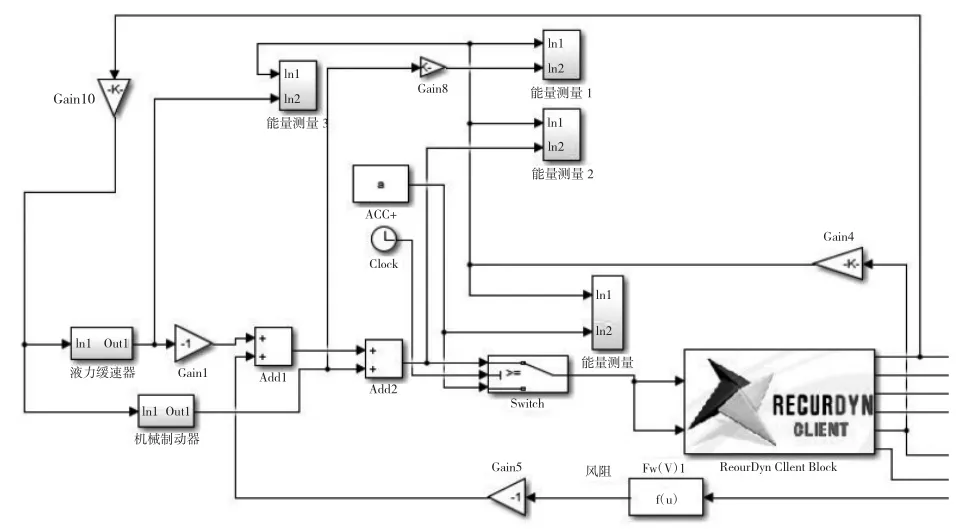
圖4 某重型履帶裝甲車輛的機械-液力制動聯合仿真模型

綜上，仿真中將制動初速度設定為65 km/h，采用符合實際工況的兩段式制動控制策略，即當履帶裝甲車輛速度為30～65 km/h 時，只使用液力緩速器制動；當履帶裝甲車輛速度為0～30 km/h 時，采用聯合制動。

3 聯合仿真與分析

仿真分為加速和制動2 個階段，當車速高于65 km/h 時立即實施兩段式制動控制。某重型履帶裝甲車輛的機械-液力制動速度圖像如圖5 所示，位移圖像如圖6 所示。

圖5 某重型履帶裝甲車輛的機械-液力制動的速度圖像

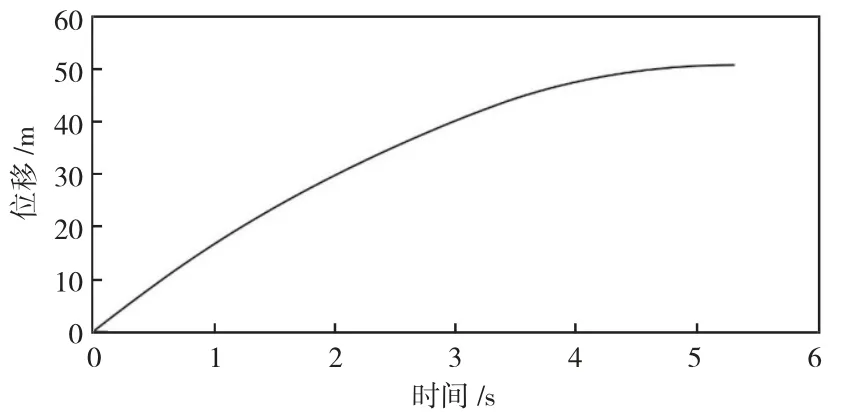
圖6 某重型履帶裝甲車輛的機械-液力制動的位移圖像

聯合制動仿真全程用時5.29 s，制動位移50.67 m，初始制動速度65.02 km/h，仿真終止時車輛速度為0。圖5 中的速度曲線沒有尖峰和震蕩，較為平滑，表明仿真符合實際制動過程。圖5 中的速度曲線在3.35 s 出現明顯的斜率改變，此時速度為29.98 km/h，在3.35 s 之前，制動系統僅采取液力制動方式制動；在3.35 s 之后，制動系統開始采取機械-液力聯合制動方式制動，仿真達到了預期效果，證明某重型履帶裝甲車輛機械- 液力聯合制動的模型建模正確。

4 結論

應用RecurDyn 軟件構建了某重型履帶裝甲車輛的動力學模型和路面模型，以及液力緩速器和機械制動器的數學模型，采用Matlab/Simulink 軟件建立了某重型履帶裝甲車輛制動系統的聯合仿真模型，設計了制動控制策略，分析了制動系統的聯合仿真結果，驗證了模型的適用性和仿真的可信性。在此基礎上，下一步計劃開展機械-液力聯合制動和機械-電力聯合制動的性能比較研究，以及制動器的改進研究。