一種正三角形結構的雙光束干涉裝置

周國全

(武漢大學 物理科學與技術學院，湖北 武漢 430072)

兩列或若干列相干光波，頻率相同，位相差恒定，振動方向一致，就能在空間相遇時相互疊加，產生光的干涉現象，其表現是在某些區域始終加強，在另一些區域則始終削弱，形成穩定的強弱分布相互間隔的現象. 干涉現象是波動獨有的特征. 不同的光學干涉裝置就是用不同的方式滿足干涉條件[1-11]. 相干光束的產生方式分為波前分割式與振幅分割式；依據干涉光束的數量分類，又分為雙光束干涉與多光束干涉；而依據場強與光程差函數的等值變量來分類，則分為等傾干涉與等厚干涉兩種類型，例如Michelson干涉儀和Fabry-Perot(F-P)干涉儀. 文獻[5-8]論述了若干等厚干涉裝置及其變異的干涉結構；文獻[9-11]描述了兩種分振幅式多光束等傾干涉結構——大頂角等腰劈與矩形腔干涉結構，而一般教科書中的等傾干涉是利用擴展光源照射在厚度不變的薄膜上產生的多光束干涉現象，不同級序的干涉條紋對應不同的傾角. 文獻[12-15] 介紹了幾種干涉結構的若干應用問題. 本文依據幾何光學與波動光學的原理，介紹和分析了一種具有正三角形結構并能產生雙光束等傾干涉的光學裝置, 但它又不同于文獻[9-11]和教科書中的平行膜多光束干涉方式. 我們推導了正三角形干涉裝置的光程差的公式及其干涉斑紋的亮暗極值條件，解析推導并分析了其干涉斑紋的分布規律，并在結語中提出尚待解決的若干開放的問題.

1 正三角形光學腔雙光束干涉光路圖

如圖1-圖4所示是一種正三角形光學腔ΔABC, 邊長為a，其中AB是全反射鏡，AC、BC是兩塊相同的能夠部分反射部分透射的平板光學玻璃, 但BC被截去一半，BO=BC/2=a/2，且腔內外空氣媒質的折射率為n0?1.00. 一般用于光學干涉實驗的無膜平板玻璃，標稱厚度大約5 mm左右. 當一束真空波長為λ的光線I以任意入射角i(入射光束被限制在30°左右)，并在BO上任意點P入射，腔外得到反射線I′，腔內部分經各邊順次反射之后形成反射回路PP1→P1P2→P2P3，其中腔內反射線P2P3(即I″ )交OC于P3；當入射光束被限制在入射角i=30°左右很小范圍，經兩次折射與反射后的出射光I″(P2P3)不經過光學玻璃BO，直接射出并和反射光

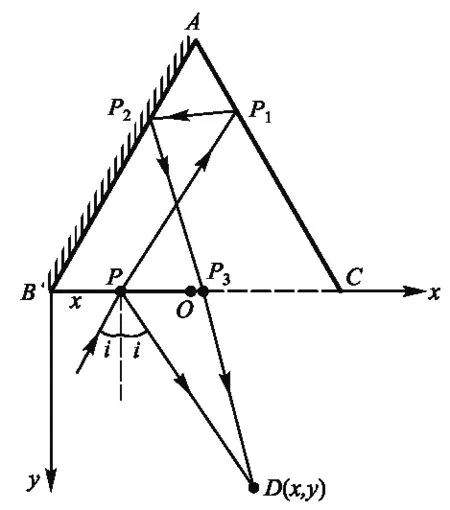
圖2 入射角i略大于30°的光路圖

交于圖1、圖2中的D點, 或圖3、圖4中的無窮遠處(或凸透鏡的焦點).

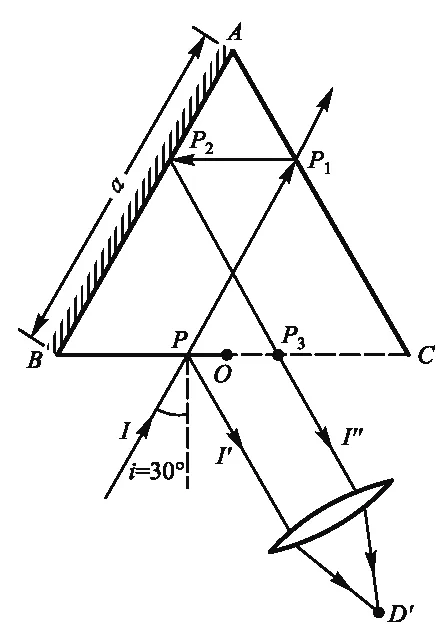
圖3 左入射i=30°時的光路圖

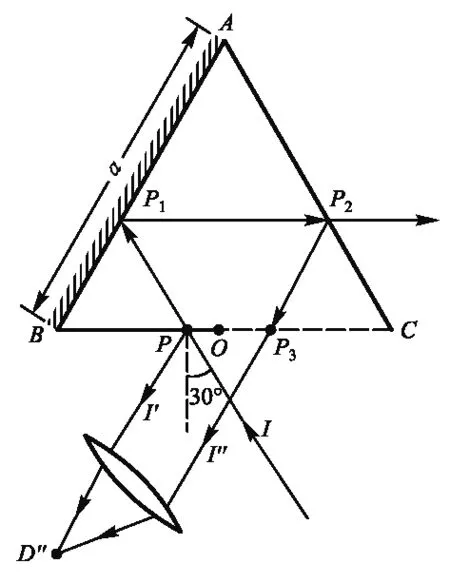
圖4 右入射i=30°時的光路圖

如圖1—圖4所示，首先可證：當入射角i略小于30°，此時反射光線I′與反射光線I″ (即P2P3) 的反向延長線交于AB上側D點；當入射角i略大于30°，反射光光線I′與反射光線I″的延長線交于BC下側D點；當入射角i=30°，反射光線I′與反射光線I″平行, 交于凸透鏡焦點D′或D″點(分別從法線左右兩側入射時) .

這是因為ΔABC為等邊三角形，∠A=∠B=∠C=60°，根據反射定律，P1處入射角為60°-i；P2處入射角為i, 且 ∠PP1C=30°+i；∠PP1P2=2(60°-i)； ∠AP1P2=∠PP1C=30°+i；∠P1P2P3=2i. 如圖1所示，當入射角i略小于30°，在ΔPP3D中, ∠DPP3=90°+i；∠DP3P=30°+i；最后推得∠PDP3=2(30°-i)；此式表明，當入射角i略小于30°，則∠PDP3=2(30°-i)>0°，說明此時反射光線I″與反射光線I′的反向延長線交于AB上側D點，如圖1所示.

當入射角i略大于30°，此時若按圖1計算，則得∠PDP3=2(30°-i)<0°，矛盾，故交點D不應在AB上方腔外，而應在BC下方的D點；如圖2所示，在ΔPP3D中, ∠DPP3=90°-i，∠DP3P=150°-i，此時∠PDP3=2(i-30°)>0，可知反射光線I″與反射光線I′的延長線確實交于BC下側的D點.

特別地，當入射角i=30°，并從法線左側入射，則∠PDP3=2(30°-i)=0°，交點D趨于無窮遠處，此時反射光線I″與反射光線I′平行，通過凸透鏡相交并干涉于其焦平面上D'點，如圖3所示. 而當入射角i=30°，并從法線右側入射，∠PDP3=2(30°-i)=0°，交點D趨于無窮遠處，此時反射光線I″與反射光線I′平行，通過凸透鏡相交并干涉于其焦平面上D″點，如圖4所示.

2 光程差公式與干涉條件

其次可證，無論反射光線I″與反射光線I′相交于D點，或無窮遠處，其幾何光程差都與入射點P的位置無關，亦即與BP=x無關，而僅依賴于入射角i及ΔABC的邊長a，因而滿足雙光束等傾干涉條件. 以入射角i略大于30°的圖2情形為例，我們推導交點D處的光程差ΔL及相位差δ的表達式，并討論其干涉條紋的亮暗條件. 從P點開始計算光程差，反射光I′的表觀光程為PD，透射光的表觀光程為PP1+P1P2+P2P3+P3D+Δ0，光程差為

ΔL=PP1+P1P2+P2P3+P3D+Δ0-PD+λ/2

(1)

其中計入了反射半波損失，而來自于半透型平板光學玻璃BO內的光線穿過一定傾斜路徑(設長為h) 所帶來的附加光程，n為半透型平板光學玻Δ0=nh璃的折射率. 它給相位差δ帶來一個常數附加δ0=2πnh/λ. 這只會給干涉斑點或條紋帶來級序或位置的平移變化，不影響干涉場整體的相對分布規律.

根據光線反射定律與平面幾何知識：∠PP1C=30°+i；∠PP1P2=2(60°-i)；∠AP1P2=∠PP1C=30°+i；∠P1PC=90°-i；∠PP1C=30°+i；∠AP1P2=∠PP1C=30°+i；∠AP2P1=90°-i；∠BP2P3=∠AP2P1=90°-i；∠BP3P2=30°+i；∠DPP3=90°-i；∠DP3P= 150°-i；∠PDP3=2(i-30°)， 在三角形ΔPP1C，ΔAP1P2，ΔBP2P3和ΔPP3D中分別運用正弦定律，并設BP=x，則PC=a-x，可分別求得：

(2)

(3)

(4)

P3D=PP3cosi/sin2(i-30°)

(5)

PD=PP3sin(30°+i)/sin2(i-30°)

(6)

PP3=(2a-x)cosi/sin(30°+i)-(x+a)

(7)

(8)

將上述式(2)—式(6)代入光程差ΔL式(1), 及相位差公式δ=2πΔL/λ，并做整理可得

(9)

(10)

特別地，當i=30°，即如圖3、圖4所示的情形，光程差ΔL與相位差δ分別為:

ΔL=3a/2+λ/2+Δ0；δ=3πa/λ+π+δ0

(11)

顯然光程差ΔL、相位差δ僅和入射角有關，并隨入射角i而變，而與BP=x無關，即與入射點P的位置無關.

綜上所述，如圖2所示，腔內外的兩束反射光相交于D點，兩束光的波長與頻率相同，并具有僅依賴于入射角與邊長的一定的光程差，滿足雙光束相干條件，應能觀察到定域于D點的亮暗干涉斑紋；由于入射角相同，光程差就相同, 從而形成雙光束等傾干涉現象. 對于級序為k的亮暗干涉斑點，當

ΔL=kλ，δ=2kπ，k∈N，亮斑.

(12)

ΔL=(k+1/2)λ，δ=2kπ，k∈N，暗斑.

(13)

其中N為正整數集合. 前述分析表明，當光束以i>30°入射時，而當光束以i<30°入射時，可憑肉眼逆著出射線，在圖1中的D點處觀察到干涉斑紋. 實際上圖1、圖2兩種情形，也可使用凸透鏡，在透鏡后觀察到定域于某點的干涉斑紋(D點經透鏡的成像點). 而當i=30°，如圖3所示(法線左側入射)，或如圖4所示(法線右側入射)，此時運用凸透鏡，兩束平行光匯聚并干涉于其焦平面上D′或D″點. 綜上所述，在圖1—圖4所示之4種情形，均可用凸透鏡觀察到干涉斑紋.

3 干涉場強分布函數與對比度分析

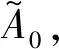
(14)

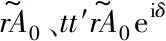
(15)

其中R=r2是半透型光學玻璃的能量反射系數. 可知D點處的干涉場的場強ID為

(16)

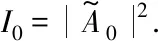
(17)

從AC膜處透射出去的光強IT為

(18)

根據式(16)中ID的表達式，當cosδ=±1時，其極大與極小值分別為:

IDmax=I0R(2-R)2；IDmax=I0R3

(19)

其中R∈[0,1]，IDmax(R)的極大值為32I0/27(當R=2/3時), 最小值為零；IDmax(R)的最大值為I0，最小值為零. 點D處干涉斑紋的明暗對比度η為

(20)

上式表明，增大玻璃板的能量透射系數，或者減小平板玻璃表面的能量反射系數R，都能增加干涉斑紋的明暗對比度; 但是結合干涉場強表達式(16)、(19)，可知能量反射系數R也不能太小，否則干涉場強ID直接趨于零了. 到底R多小為宜？顯然R的選取應在增強明暗對比度η與增強條紋最大光強IDmax的兩難選擇之間達到某種平衡.

4 干涉斑紋的位置分布及其間隔

仍以入射角i>30°，i≈30° 的圖2情形為例，如圖2所示，取BC邊為直角坐標系的X軸，點B為直角坐標系的原點，過原點B的Y軸垂直于BC邊并朝下(為方便起見，選定左手系). 不妨設Δ0=0，設第k級暗斑Dk的入射角為ik, 則

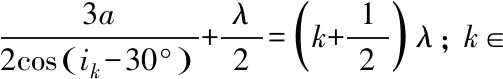
(21)

可求出

cos(ik-30°)=3a/2kλ

(22)

由此可知干涉級序k值受限于3a/2kλ≤1；k∈, 即kmin=[3a/2λ]，中括弧意即圓整為整數. cos(ik-30°)=1即相應于ik=30°的平行光干涉的情形(D點趨向于無窮遠處，用凸透鏡可觀察干涉現象)，此時具有最低干涉級序kmin. 注意為使反射光線P2P3(I″)能在OC之間無障礙射出，i，x須滿足條件:

a/2≤BP3=x+PP3≤a

(23)

可得P點位置x的極大值

(24)

及其允許范圍0≤x≤xmax≤a/2, 由此可得其實驗觀察允許的入射角范圍為

16.10°≤ik≤43.90°

(25)

具體而言，圖2情形(ik≥30.00°)的實像干涉情形的允許入射角范圍為

30°≤ik≤43.90°

(25)

而圖1所示(ik<30.00°)的虛像干涉情形的允許入射角范圍為

16.10°≤ik<30.00°

(26)

由式(22)又可求出

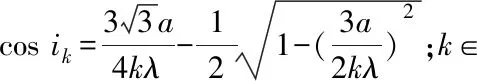
(27)

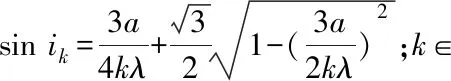
(28)

則干涉場的暗斑Dk的坐標(Xk,Yk)為

Xk(x,i)=x+PDsinik=

(29)

Yk(x,ik)=PDcosik=

(30)

從式(29，30)易知Dk的含參數的軌跡方程為

Xk(x,ik)=x+Yk(x,ik)tanik

(31)

由于相位差與P點位置即x無關，再由式(27-29)可知，在ik不變時，入射點P的平移不會改變干涉級序k值，但第k級暗斑的位置將在一條直線段上連續移動，形成暗紋，如圖5所示.

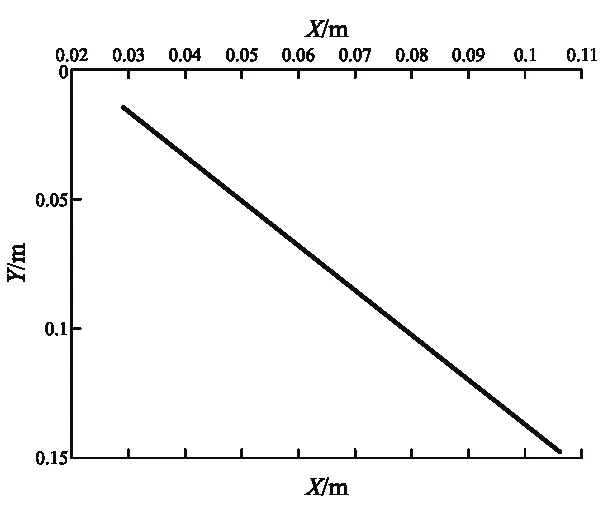
圖5 第k級暗斑隨入射點x的移動而形成暗紋(干涉級序k=119100；a=0.05 cm；ik=36.65°)

另一方面，在保持入射點P不動，即x不變的條件下，改變入射角i，使之滿足不同級序k的暗斑條件i=ik,k=119100+i,i=0,1,2,…7；取定腔體邊長數a=5 cm；入射點x=a/4；入射波長λ=632.8 nm，用軟件繪制出暗斑分布圖Xk(ik)-Yk(ik)，如圖6所示. 尤須指出，從式(31)可知, 因為tanik隨不同級序k值而變，Xk(ik)與Yk(ik)之間并不是線性關系，斑點的分布圖形嚴格而言并不是直線，但由于圖6中所取的k值范圍使得式(31)中tanik近似不變，因此不同級序干涉斑點分布的局部軌跡近似于一段直線.

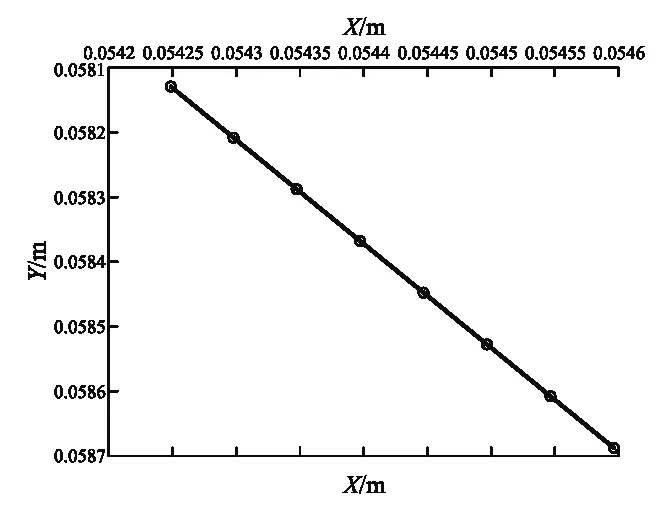
圖6 固定入射點x時，不同級序斑點的分布圖(參數a=5 cm, λ=632.8 nm；x=a/4；斑點級序：k=119100+i; i=0,1,2,…，7；入射角近35)

下面再計算相鄰第k級、k+1級干涉暗斑的間隔dk=DkDk+1，即Dk(Xk(x,ik),Yk(x,ik))與Dk+1(Xk+1(x,ik+1),Yk+1(x,ik+1))的間距dk為

dk(x,a,λ;k)=DkDk+1=

(32)

將式(29，30)分別代入tanik=sinik/cosik及式(32)，即得距離dk的嚴格解析表達式；而式(32)僅在tanik?tanik+1的情況下近似成立.

前述間距公式表明：相鄰干涉斑點的間隔與級序k值或入射角(ik,ik+1)有關，并與x,a,λ有關. 如欲使干涉斑紋肉眼可辨，須使相鄰斑紋的間隔dk(x,a,λ;k)≥1 mm; 這就是腔體尺寸a與波長λ、級序k所須滿足的條件. 如果相鄰斑紋的間隔很小，則須用讀數顯微鏡進行觀測. 為使讀者有一個簡單而直觀的印象，不妨取λ=632.8 nm, 在不用凸透鏡觀察的情況下，我們分別在三種情形給出如下參考數據：1)a=5 cm(宏觀情形)，入射點P在BO的中點:x=a/4,k=119100，ik=35.65°，斑紋位置在Dk(5.46 cm,5.87 cm)；相鄰條紋間隔dk=8.29 cm；2)a=7.5 μm (微觀情形)，x=a/8，k=18，ik=39.01°，斑紋位置在Dk(7.1 μm,7.7 μm)；相鄰條紋間隔dk=9.5 μm；3) 而對于腔體邊長a=1 mm的中間尺度情形x=a/4，k=2371，ik=31.27°，斑紋位置在Dk(3.0 mm,7.7 mm)；相鄰條紋間dk=9.1 mm, 顯然肉眼可辨. 另一方面，理論分析與計算表明，在保持a，λ及入射點x不變的前提下，隨著級序k值增加，入射角ik也增加，斑紋坐標值減小，斑紋位置離裝置(入射點P)越近，斑紋處相鄰條紋間隔也越小；反之，隨著k值和入射角ik(從最大允許入射角43.9)逐漸減小，斑紋位置離裝置(入射點P)越遠，斑紋處相鄰條紋間隔dk也越大，直至ik減小至30°，斑紋位置趨于無窮遠處，此時干涉級序k值有最小值，kmin=[3a/2λ]，一般用凸透鏡觀察平行光的干涉現象，如圖3、圖4所示.

5 可能的應用前景

這種干涉結構不僅在光學科研與教學方面具有理論研究的意義，而且具備技術應用的現實可能性. 在以i=30°入射時，根據其光程差公式與干涉斑點亮暗條件(11-13)，如能讓平板玻璃AC沿著BC方向(X軸方向)平移，或者讓BO光學板沿著垂線AO方向(Y軸方向)平移，就能在各自平移過程中保持ABC為正三角形. 如此則通過D(D′、D″)處干涉斑點的吞吐數目ΔN，配置以機械傳動裝置，即可實現對邊長AB方向和高線AO方向位移的光學傳感，精度可達1 μm；如果在記錄亮(暗)斑吞(吐)的數目ΔN的同時又記錄其所花時間Δt，則可同時實現對二維微位移速度的傳感測量. 而且這種等邊三角干涉裝置結構對稱，操作簡便. 當然這種干涉結構對其位移傳感量程的限制，在于不能讓光線超出各自的合理范圍或者逸出透鏡的接收孔徑.

另一方面，對于給定尺寸的正三角結構光學干涉腔，按照圖3、圖4的i=30°單色平行光入射方式實現雙光束干涉，也可以根據干涉明暗條件(11-13)，很方便地測定入射光波長，或者反過來測定正三角形光學腔的結構參數——邊長a或高線長. 對于非30°入射情形的可能應用，尚有待于作者的繼續研究與讀者的發現.

6 結語

研究表明，本文給出的正三角形干涉結構，當光線在i～30°附近入射的情況下，確實能夠發生雙光束干涉現象. 當i=30°時，干涉場定域于無窮遠，可以運用凸透鏡觀測；當i≠30°時干涉場定域于有限遠處，也可在凸透鏡后側觀察到干涉斑紋. 本文推導了正三角形雙光束干涉結構的光程差與相位差、及干涉場強與對比度的公式，分析討論了干涉斑紋的極大與極小條件及其觀察方法，定量地推導與分析了干涉斑紋的分布規律，特別是相鄰條紋間隔公式，并討論了其可能的應用前景.

當然，由于時間與經費的限制，我們目前的研究還僅限于入射光線在正三角腔的橫截面(即紙面)情形的初步理論探索. 后續的工作將專注于實驗對理論的檢驗工作，以及隨之而來的一個自然產生的問題：當入射角ik～30°，且在保持ik不變的情況下，入射光線繞法線旋進若干角度，干涉斑紋又將如何變形？這個開放的問題，留待感興趣的同仁賜教.