醫用微型膠囊機器人雙變量磁力矩控制研究*
楚 莊,王元利,遲明路,劉榮升,錢曉艷,邢 倩,邱亞琴,任沁超,任瑞華
(1.河南工學院 材料科學與工程學院,河南 新鄉 453003;2.河南工學院 智能工程學院,河南 新鄉 453003;3.河南工學院 經濟學院,河南 新鄉 453003;4.江蘇匯博機器人技術股份有限公司,江蘇 蘇州 215121)
0 引言
目前,使用醫用微型膠囊機器人對消化道疾病進行診治是全世界公認的最有效手段。一般膠囊機器人是在適合人體吞咽的膠囊內嵌入微型攝像頭以每秒幾幀的速度對消化道內壁拍攝照片[2],并通過無線傳輸的方式將照片傳送給體外接收設備,便于醫生進行初步篩查。與傳統內鏡相比,膠囊機器人具有安全、無創等特點[3,4]。但一般膠囊機器人嚴重依賴于腸道蠕動力,無法自我推進,甚至還存在漏檢和滯留人體內的危害,這些不足限制了膠囊機器人的廣泛應用[5,6]。本文提出一種磁控主動式螺旋醫用微型膠囊機器人及雙變量磁力矩解耦控制方法,通過解耦坐標變換將控制變量由三個減少為兩個,進而達到解耦控制的目的。通過分析俯仰角和側擺角與磁力矩相互關系可知,俯仰角和側擺角都與微型膠囊機器人的運動方向有關。俯仰角和側擺角越接近0°,微型膠囊機器人的運動狀態越穩定。當俯仰角和側擺角同時等于0°時,平均總磁力矩達到最小值。控制變量的解耦降維控制方法具有操作簡便的特點,使轉彎磁力矩分析、計算過程變得簡單,提高了磁場控制的可操作性與實用性,為以后的彎曲環境內軌跡規劃、磁力矩分析及運動控制奠定了理論基礎。
1 醫用微型膠囊機器人驅動原理與結構
1.1 醫用微型膠囊機器人結構
該機器人結構簡單緊湊,如圖1所示,能夠很好地適應人體胃腸道柔彈性大、結構彎曲復雜等特點。其主要由覆有螺旋肋的瓦片、永磁體和端蓋構成。機器人旋轉運動時與消化道內壁長時間接觸,需要具有足夠安全的生物相容性,對人體無毒害刺激作用,因此本設計中,微型膠囊機器人外殼選用可生物降解的PLA材料進行3D打印,極大地保證了人體健康安全。參考目前國際上使用的微型膠囊機器人尺寸[7,8],本文中微型膠囊機器人本體總長為26 mm,直徑為12 mm,螺旋升角為45°,螺旋肋高1 mm。
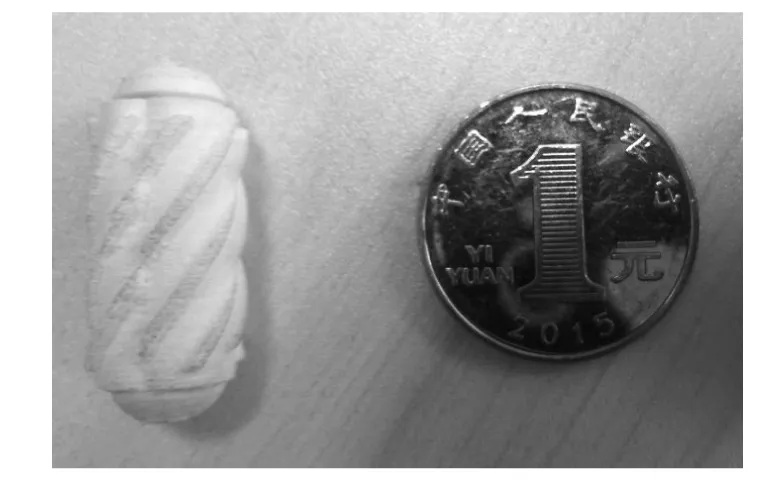
圖1 微型膠囊機器人結構圖
1.2 微型膠囊機器人驅動原理
為了有效驅動微型膠囊機器人在腸道空間環境內進行自主運動,實現人體消化道的安全診察工作,利用三軸Helmholtz(亥姆霍茲)線圈電磁驅動系統控制微型膠囊機器人的前進、后退及轉彎,如圖2所示。微型膠囊機器人電磁驅動系統整體由微型膠囊機器人本體A、磁場發生系統B、電磁控制系統C、視頻監控系統D和人機交互系統E五部分組成。該系統通過磁場法向量在坐標系內的俯仰角和側擺角雙變量進行磁場方位控制,實現機器人在人體消化道內的位姿變化。
Helmholtz線圈由一對位于同一軸線上、線圈之間的間距等于它們半徑的平行線圈組成,兩線圈具有相同的匝數和繞線方式。在Helmholtz線圈的中心區域能形成一定范圍的勻強磁場,向兩線圈通入同向電流時會增大磁場強度。三對線圈由外到內、從大到小嵌套組合而成的Helmholtz線圈叫做三軸Helmholtz線圈。基于交變磁矢量疊加原理[9,10],向三軸線圈通入符合一定相位和幅值關系的電流,就能夠在中心區域產生方位為n的動態旋轉磁場。
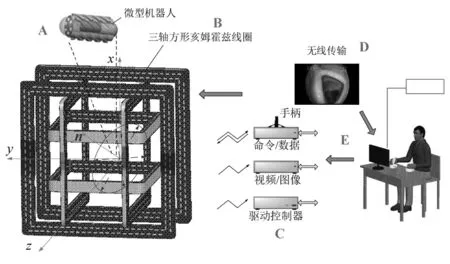
圖2 電磁驅動系統示意圖
2 三維空間磁場控制特性
2.1 方形Helmholtz線圈磁場的產生
方形Helmholtz線圈指的是一對相同的、共軸的、彼此平行且繞有N匝線圈的正方形載流線圈。在方形線圈上建立如圖3所示的坐標系。x軸、y軸為線圈邊長方向,z軸為線圈中心軸方向。Bx、By、Bz為線圈在x軸、y軸和z軸三個方向的磁場分量。方形Helmholtz線圈的邊長為2a,線圈的距離為2d,電流為I,z軸方向與電流方向形成右手螺旋關系。
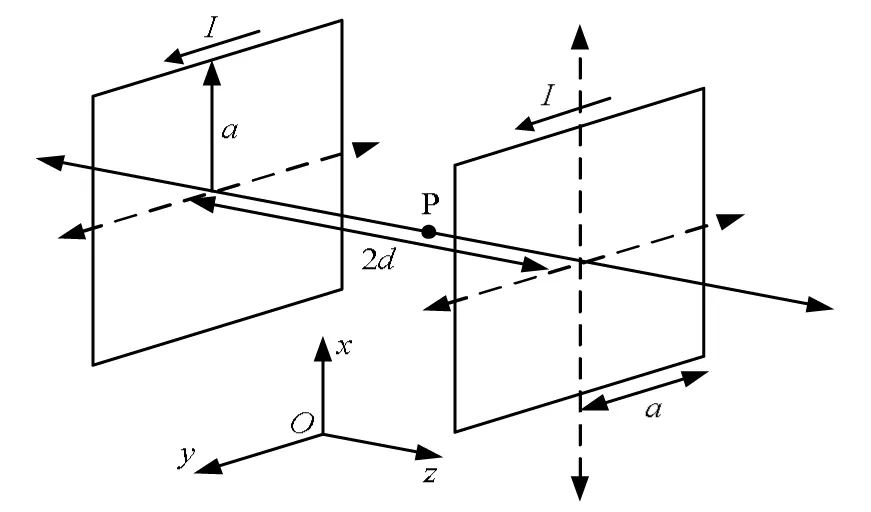
圖3 單軸方形Helmholtz線圈示意圖
中心軸線上P處產生的磁感應強度大小為:
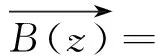
(1)
為了產生較強的磁場,增大線圈厚度形成厚壁線圈。圖4為標準的厚壁方形Helmholtz線圈結構圖。忽略線圈繞線的螺旋性,并假設繞線均勻。
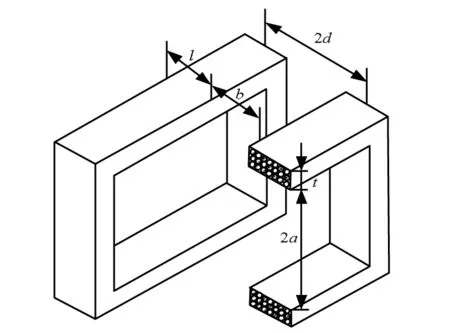
圖4 單軸方形Helmholtz線圈
考慮實際Helmholtz線圈的厚度和匝數,單軸方形Helmholtz線圈中心點磁感應強度與電流及線圈結構參數之間的關系可以寫成:

(2)
式中,t為線圈的厚度,l為線圈寬度,b為線圈的間距,真空磁導率μ0=4π×10-7H/m,Ki為各單軸方形Helmholtz線圈的結構系數,
i=1,2,3。
Helmholtz線圈內導線匝數N為:
(3)
式中,線圈底層繞線匝數為N11=l/(kηd′),kη為導線排繞系數,kη=1.05;線圈繞線層數為N22=t/(kβd′),kβ為導線疊繞系數,kβ=1.02,d′是含絕緣線的線徑。
綜上分析,磁感應強度幅值B0與電流幅值有如下關系:
B0=KiIi,i=1,2,3
(4)
式中,i=1,2,3分別表示小線圈、中線圈和大線圈。
2.2 Helmholtz線圈電學參數
線圈凹槽內導線的平均匝長為:
la=2(π(r+t/2)+4a-4r)
(5)
式中,r為過渡圓角半徑。
單軸線圈電阻為:
(6)
式中,ρ0為導線的電阻率,ρ0=1.71×10-8Ω·m,s0為線圈導線線徑橫截面積,d0為導線裸線直徑。
單軸Helmholtz線圈的電感為:
Li=2L0i+2Mii=1,2,3
(7)
式中,L0i為自感,Mi為互感,則有

單軸線圈的重量為:
(8)
式中,ρ為線圈導線的密度。
3 雙變量磁場疊加原理與仿真分析
3.1 解耦坐標變換
矢量在空間某個平面內旋轉時,該平面可由xoz平面經過側擺和俯仰的運動來獲得,而y軸經過相同的側擺俯仰變換后得到旋轉平面的法向量。因此,采用正交變換,以磁場軸線在經緯坐標系內的側擺角與俯仰角為控制變量的三相正弦波電流,在三軸正交嵌套Helmholtz線圈內疊加出方向可分別沿側擺和俯仰方向獨立調整的均勻旋轉磁場。
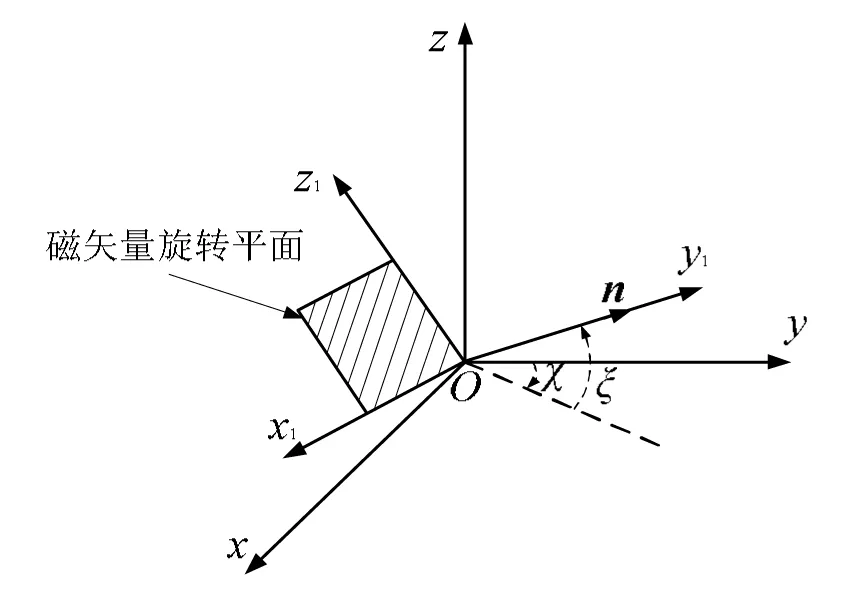
圖5 旋轉坐標變換關系
如圖5所示,在固定坐標系中,xoz平面旋轉的磁矢量經過正交變換后,繞z軸旋轉χ角,再繞x1軸旋轉ξ角,磁矢量將在x1oz1平面內旋轉。而旋轉平面的法向量由y軸變為方向向量n(sinχcosξ,cosχcosξ,sinξ),因此正交變換矩陣可表示為:
A=Rot(x1,ξ)Rot(z,-χ)

(9)
3.2 雙變量轉彎磁力矩
磁感應強度在動坐標系ox1y1z1中的分量為:
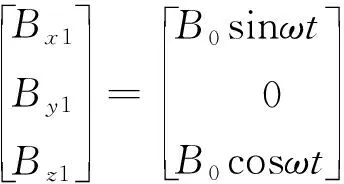
(10)
若想產生右旋旋轉磁場,在固定坐標系中,磁感應強度分量為:
(11)
正交變換矩陣的逆矩陣可計算為:
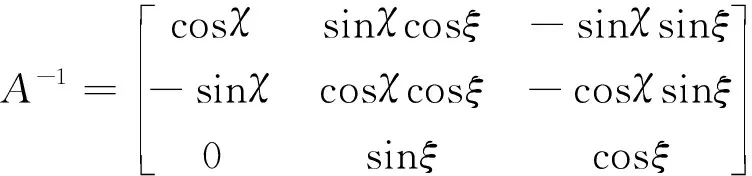
(12)
因此,由式(11)和式(12)可得固定坐標系oxyz的磁感應強度為:
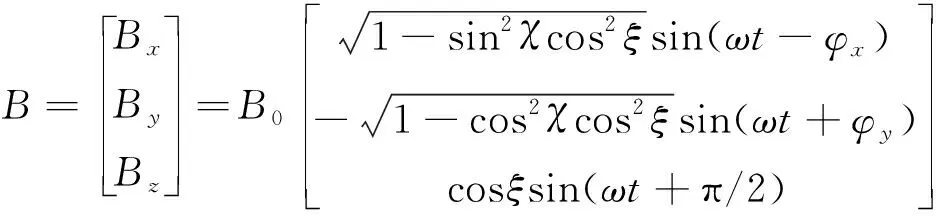
(13)
式中,χ、ξ分別為磁場旋轉軸線在經緯坐標系下的側擺角與俯仰角,tanφx=tanχsinξ,tanφy=cotχsinξ。為使向量n指向空間任意象限,側擺角χ的取值范圍為(0°,360°),俯仰角ξ的取值范圍為(-90°,90°)。
此時永磁體的磁矩矢量可表示成:
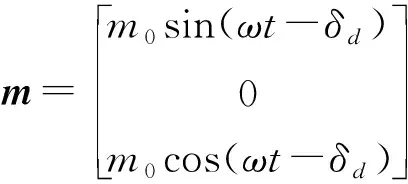
(14)
式中,δd為轉差角。由磁耦合力矩公式,雙變量轉彎磁力矩可表示為:

(15)
由式(15)知,當微型膠囊機器人在直管中運動時,俯仰角ξ和側擺角χ均為0°,此時的微型膠囊機器人軸線與旋轉磁場軸線重合,則直管內耦合磁力矩為:
T=m0·B0·sinδd
(16)
3.3 磁力矩仿真分析
俯仰角和側擺角對各磁力矩分量的影響如圖6(a) — (d)所示,由圖可知,俯仰角和側擺角對Tx和Ty均有影響,而Tz僅受俯仰角影響,受側擺角的影響不大。當俯仰角為0°時,側擺角不會改變微型膠囊機器人運動方向;當俯仰角接近-90°或90°時,微型膠囊機器人運動時將會隨著側擺角的增大而擺動。
綜上分析,俯仰角和側擺角都與膠囊機器人的運動方向有關,都會影響微型膠囊機器人的運動狀態,俯仰角和側擺角越接近0°,微型膠囊機器人的運動狀態越穩定。當俯仰角和側擺角等于0°時,微型膠囊機器人將沿自身軸線旋轉并進行直線運動,符合式(16)的計算結果。顯然,當俯仰角和側擺角等于-90°或90°時,平均總磁力矩達到最大值;平均總磁力矩隨俯仰角和側擺角的減小而減小,當俯仰角和側擺角同時等于0°時,平均總磁力矩達到最小值。
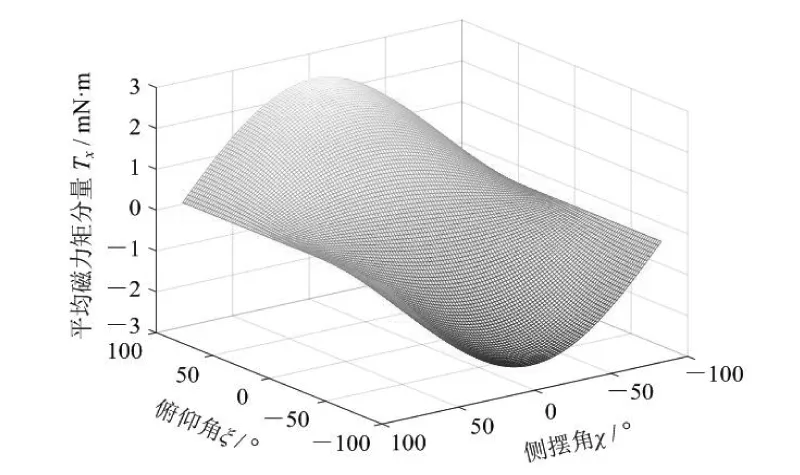
(a) 俯仰角、側擺角對Tx的影響
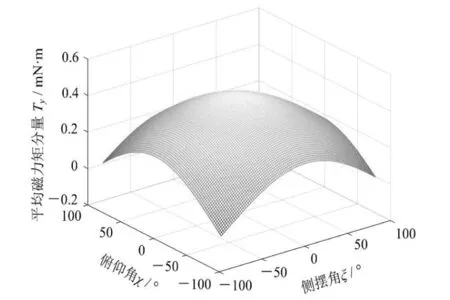
(b) 俯仰角、側擺角對Ty的影響
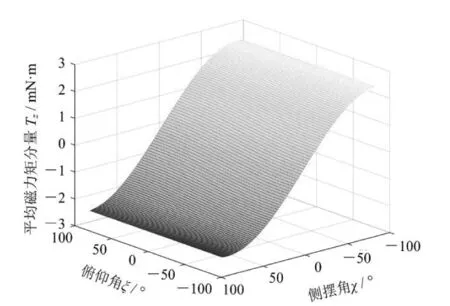
(c) 俯仰角、側擺角對Tz的影響
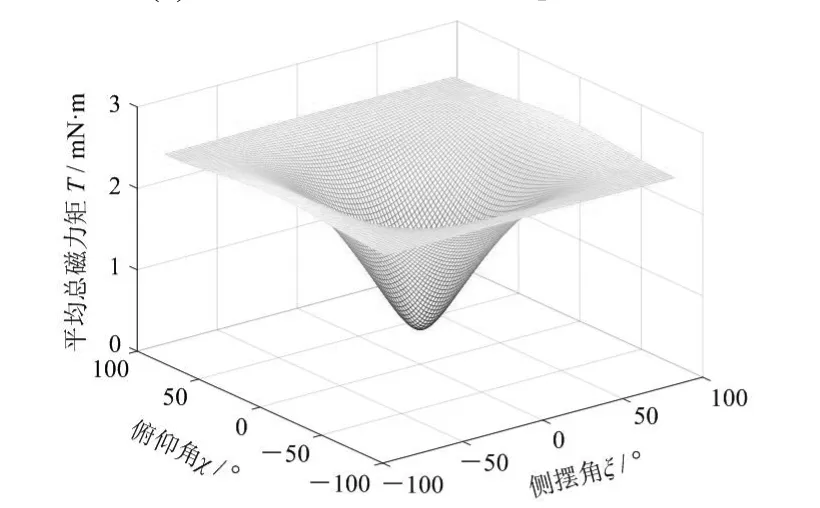
(d) 俯仰角、側擺角對T的影響圖6 俯仰角、側擺角對各磁力矩分量的影響
4 結論
本文對醫用微型膠囊機器人雙變量轉彎磁力矩進行了研究,提出了一種磁控主動式螺旋醫用微型膠囊機器人及雙變量磁力矩解耦控制方法。由于微型膠囊機器人三個姿態角的存在,造成機器人控制復雜,與常規控制方式不同,控制變量的解耦降維控制方法具有操作簡便的特點,簡化了轉彎磁力矩的計算和分析過程,提高了磁場控制的可操作性與實用性。分析結果表明:俯仰角和側擺角均與微型膠囊機器人的運動方向有關。俯仰角和側擺角直接影響微型膠囊機器人的平均總磁力矩。當俯仰角和側擺角等于0°時,微型膠囊機器人進行直線運動,此時的平均總磁力矩達到最小值。研究結果為以后微型膠囊機器人彎曲環境內軌跡規劃、磁力矩分析及運動控制奠定了理論基礎。

