基于有限差分法的低溫防護(hù)服優(yōu)化設(shè)計(jì)及仿真*

張建霞,邵創(chuàng)新,田 坤

(河南工學(xué)院 智能工程學(xué)院,河南 新鄉(xiāng) 453003)

0 引言

隨著科學(xué)技術(shù)的發(fā)展,人類在低溫環(huán)境下進(jìn)行作業(yè)的場(chǎng)合越來越多[1]。眾所周知,人長(zhǎng)時(shí)間處于低溫環(huán)境中,熱量會(huì)快速消散,進(jìn)而出現(xiàn)一些不適,如心跳過快、呼吸不規(guī)律和動(dòng)作不靈活等[2-5],嚴(yán)重時(shí)甚至威脅生命安全。為了能夠很好地在低溫環(huán)境下作業(yè),科學(xué)家們展開了對(duì)低溫防護(hù)復(fù)合材料的研究,試圖做成防護(hù)服以保護(hù)在低溫環(huán)境下的工作者[6-8]。低溫防護(hù)服的復(fù)合材料一般具有三層結(jié)構(gòu),分別是內(nèi)層織物層、中間層功能層和外層隔熱層[9]。內(nèi)層織物層主要提供舒適性;中間層由一種特殊的材料即相變材料構(gòu)成,其可以產(chǎn)生并釋放熱量,用以延緩人體溫度降低;外層隔熱層主要是延緩熱量對(duì)外傳遞。低溫防護(hù)服在短時(shí)間內(nèi)能有效降低低溫環(huán)境對(duì)人體的傷害[10-12]。

本文針對(duì)如何有效提高低溫防護(hù)服的耐低溫性進(jìn)行研究。首先,基于非穩(wěn)態(tài)傳熱微分方程建立熱傳導(dǎo)模型;然后,利用函數(shù)方程插值擬合、二次搜索算法與有限差分法進(jìn)行分析求解;最后,通過Matlab平臺(tái)進(jìn)行仿真得到低溫防護(hù)服使用時(shí)間及最優(yōu)厚度參數(shù)。

1 不同條件下問題的闡述與分析

本文數(shù)據(jù)主要來源于2020年華數(shù)杯高校大學(xué)生數(shù)學(xué)建模競(jìng)賽主辦方[13]。為了更方便地對(duì)相關(guān)參數(shù)進(jìn)行求解并高效地解決問題,提出以下假設(shè):(1)不考慮其他不均勻熱源和傳熱過程;(2)不考慮接觸面之間的接觸熱阻,認(rèn)為接觸面連續(xù);(3)不考慮作業(yè)服水汽、汗液蒸發(fā)等對(duì)傳熱傳質(zhì)過程的影響;(4)不同厚度的服裝表面積相同;(5)消耗的衣料面積是人體表面積的1.25倍。

在以上假設(shè)的基礎(chǔ)上,具體約束分析如下:

條件(1):無風(fēng),-40℃。已給定各層材料厚度及環(huán)境溫度,通過測(cè)試得到三層材料的厚度、比熱、導(dǎo)熱系數(shù)和密度等信息。求解溫度隨時(shí)間分布,需要綜合考慮各種傳熱方式及邊界條件,建立完整的傳熱模型。通過傳熱模型建立時(shí)間與實(shí)測(cè)溫度的分布關(guān)系,仿真得到一維熱傳導(dǎo)熱量分布圖,進(jìn)而分析出下降到某一溫度的具體時(shí)間。低溫防護(hù)服傳熱模型考慮的是非穩(wěn)態(tài)傳熱,即需要建立溫度與時(shí)間的關(guān)系,得到整個(gè)傳熱過程的具體時(shí)間描述,得到非穩(wěn)態(tài)過程的溫度分布及傳熱特性。

條件(2):無風(fēng),-40℃,最大承重100kg。考慮研發(fā)制作成本、作業(yè)服笨重程度和人體舒適程度等因素建立優(yōu)化目標(biāo)。同樣考慮最大承受重量、資金增加不超過原支出的50%和厚度范圍作為約束條件,建立多目標(biāo)優(yōu)化模型。以站立時(shí)間最長(zhǎng)為優(yōu)化目標(biāo),以在特定低溫環(huán)境下隔熱達(dá)到一定效果為制約條件,求取非線性優(yōu)化函數(shù)的最優(yōu)解,得出最佳的厚度設(shè)計(jì)方案。

條件(3):無風(fēng),-40℃,最大承重100kg,增加在低溫環(huán)境下的站立時(shí)間。改變中間層的放熱能力,且各個(gè)層的溫度放熱能力同時(shí)放大同一倍數(shù),使得實(shí)驗(yàn)者在低溫環(huán)境下堅(jiān)持的時(shí)間長(zhǎng)于條件(2)中堅(jiān)持的時(shí)間。由于條件(1)下的模型已經(jīng)建立,可設(shè)放熱能力為之前的n倍,先通過大步長(zhǎng)遍歷得到一個(gè)范圍,再通過小步長(zhǎng)遍歷得到精確放大倍數(shù),使得堅(jiān)持時(shí)間大于條件(2)的時(shí)間。

2 基于非穩(wěn)態(tài)傳熱微分方程的模型建立

本文建立的熱傳導(dǎo)模型分為低溫防護(hù)服不同材料的熱傳導(dǎo)和防護(hù)服IV層到實(shí)驗(yàn)者皮膚的熱傳導(dǎo)模型兩種。由于各材料之間的距離大概在0.3—0.7mm之間,需要考慮的傳熱方式為熱傳導(dǎo)和熱對(duì)流[14-16]。

對(duì)于條件(1)的情況,考慮環(huán)境溫度通過低溫防護(hù)服到實(shí)驗(yàn)者皮膚的整個(gè)熱傳導(dǎo)需要,對(duì)數(shù)據(jù)進(jìn)行處理,得出溫度與放熱能力擬合關(guān)系,然后建立低溫防護(hù)服不同材料的熱傳導(dǎo)和防護(hù)服IV層到實(shí)驗(yàn)者皮膚的熱傳導(dǎo)模型。

明確環(huán)境溫度即為I層左側(cè)開始傳導(dǎo)溫度,IV層右側(cè)即為實(shí)驗(yàn)者皮膚溫度,通過數(shù)據(jù)可得到中間層溫度為20.622℃,開始逐漸放熱。對(duì)數(shù)據(jù)進(jìn)行五階擬合,具體關(guān)系如圖1所示。

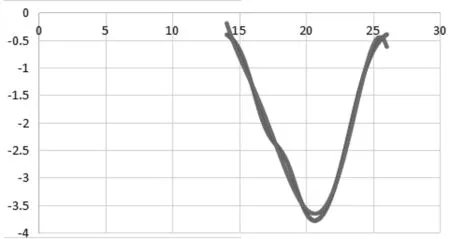
圖1 溫度與放熱能力擬合關(guān)系圖

建立低溫防護(hù)服和人體的三維模型,其具有以下特征:(1)邊界條件均勻分布,熱傳遞可看做只在一個(gè)方向進(jìn)行,即垂直于皮膚表面;(2)無其他不均勻熱源及傳熱過程,研究三維傳熱意義不大。綜合以上特征,建立一維非穩(wěn)態(tài)傳熱模型,如圖2所示。

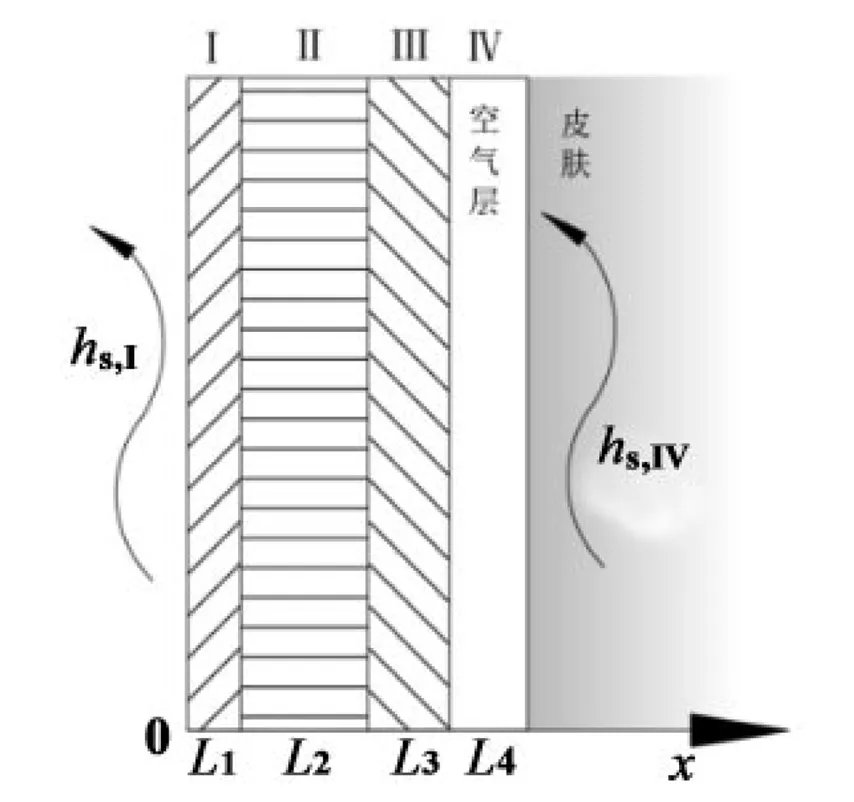
圖2 一維傳導(dǎo)模型示意圖

圖中,hs代表對(duì)流換熱系數(shù),x代表空間坐標(biāo)。一維傳熱模型不考慮上、下方向的熱傳導(dǎo),溫度變化只隨坐標(biāo)x發(fā)生變化。

對(duì)流換熱系數(shù)hs的值如表1所示。

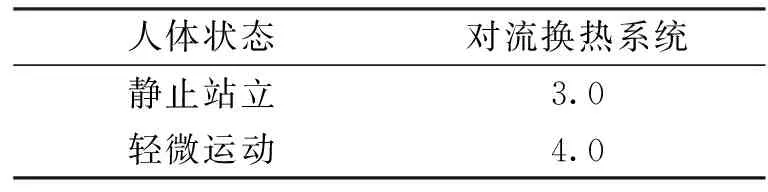
表1 對(duì)流換熱系數(shù)表

通過邊界條件值的確定以及傅里葉傳熱定律推導(dǎo)[17-20],建立一維熱傳導(dǎo)正問題模型如公式(1)所示:

(1)

式中,q代表熱流密度,i代表不同的接觸面,k代表傳熱系數(shù),hc,1和hs,4分別表示兩端的對(duì)流傳熱系數(shù),Ten表示環(huán)境溫度,Tren表示人體溫度。

對(duì)于條件(2)的情況,最優(yōu)低溫防護(hù)服的厚度設(shè)計(jì)應(yīng)該使實(shí)驗(yàn)者在低溫環(huán)境中站立時(shí)間盡可能地長(zhǎng),建立站立時(shí)間與防護(hù)服厚度L的多元目標(biāo)規(guī)劃模型,然后進(jìn)行分析求解。通過數(shù)據(jù)及假設(shè)條件得到相關(guān)約束,如公式(2)所示:

(2)

式中,V表示體積,Ab表示人體有效表面積,L表示防護(hù)服材料的厚度,m表示質(zhì)量,ρ表示密度,y表示各層防護(hù)服的價(jià)格,Y表示防護(hù)服的總價(jià)格,h表示身高,w表示體重,S表示人體表面積。

在相關(guān)約束條件下,服裝的成本和重量是設(shè)計(jì)服裝的限制條件[21]。因此將適應(yīng)度函數(shù)轉(zhuǎn)化成在有限厚度條件內(nèi),盡可能延長(zhǎng)服裝內(nèi)側(cè)溫度降到15℃的時(shí)間。在條件(1)模型建立的基礎(chǔ)之上,建立多目標(biāo)函數(shù),如公式(3)所示:

[obj]maxT(x,t)

(3)

對(duì)于條件(3)的情況,在成本限制條件下,增加在低溫環(huán)境下的活動(dòng)時(shí)間,即在條件(2)的基礎(chǔ)上進(jìn)一步優(yōu)化,提高中間層的放熱能力。通過Matlab繪圖可得出k倍中間層放熱能力優(yōu)化的擬合關(guān)系,如圖3所示。

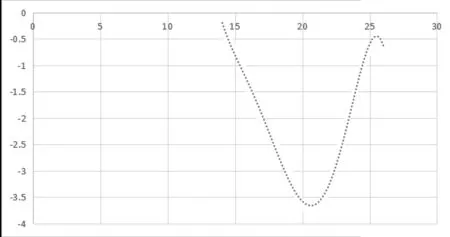
圖3 k倍中間層放熱能力擬合圖

在各種約束條件的限制下,在條件(2)模型建立的基礎(chǔ)之上,建立多目標(biāo)函數(shù),如公式(4)所示:

(4)

3 仿真實(shí)驗(yàn)

對(duì)于條件(1)而言,求解熱傳導(dǎo)反問題其實(shí)是正問題和優(yōu)化問題的結(jié)合[22]。根據(jù)一定的更新方式進(jìn)行正問題迭代,直到滿足條件為止,求得最優(yōu)解。因此正問題的準(zhǔn)確計(jì)算是能夠反推反問題中待確定值的前提,正問題的求解流程如圖4所示。

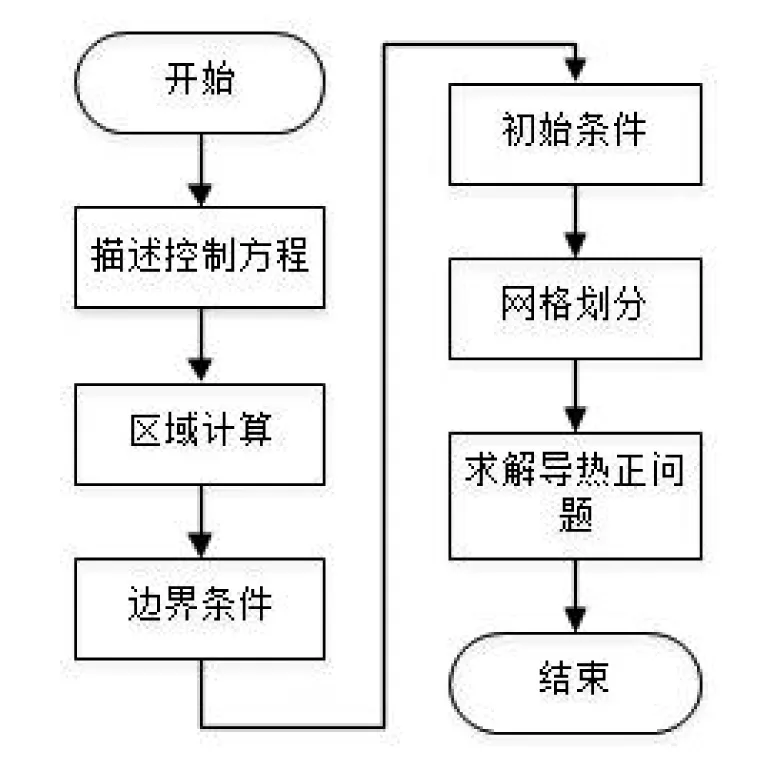
圖4 正問題模型求解流程圖

由于熱量交換的邊界條件比較復(fù)雜,熱傳導(dǎo)的偏微分方程也是多階的,因此無法用一般的解析法求解,故選用有限差分法求解一維熱傳導(dǎo)方程[23-24]。為了方便計(jì)算,采用連續(xù)變量離散化的思想,將hc,1的取值離散化,設(shè)計(jì)基于連續(xù)變量離散化的二次搜索算法。具體算法流程如圖5所示。

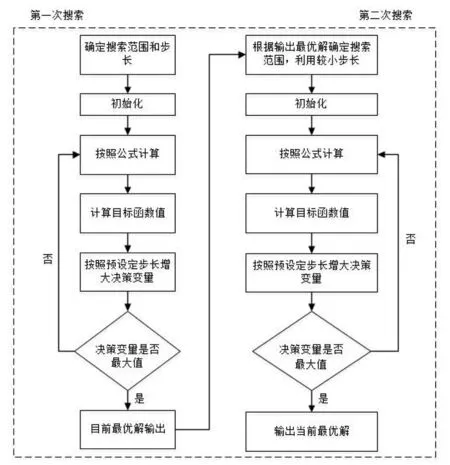
圖5 二次搜索算法程序流程圖

利用Matlab平臺(tái)進(jìn)行優(yōu)化求解,如圖6所示。

從圖6可以直觀看出溫度隨著時(shí)間變化的分布,在t1=17.79min時(shí)服裝內(nèi)側(cè)溫度降到15℃,為了安全起見,需要返回到較高溫度環(huán)境中。

對(duì)于條件(2)而言,熱擴(kuò)散系數(shù)αi(i=1,2,3)通過Matlab計(jì)算得到,進(jìn)而可得出各層放熱能力的大小,如表2所示。

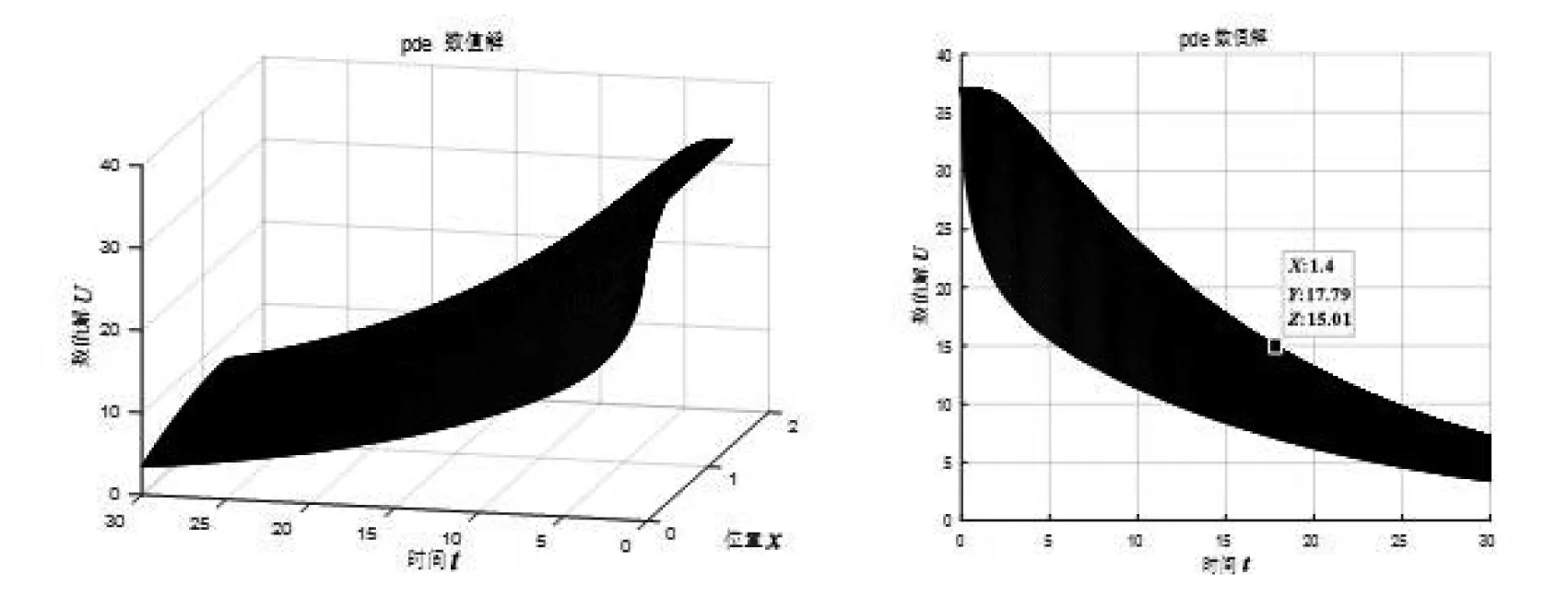
(a) 條件(1)約束下的三維圖 (b) 條件(1)約束下的平面圖圖6 條件(1)約束下的熱量分布優(yōu)化圖

表2 各層熱擴(kuò)散系數(shù)表

在滿足相同傳熱性能且制作成本降低1.5倍的條件下進(jìn)行厚度方案設(shè)計(jì)。因?yàn)橹虚g層的價(jià)格與面積有關(guān),而增加中間層的厚度幾乎不影響表面積,卻可以增加低溫防護(hù)服的御寒能力,所以設(shè)計(jì)中間層最大厚度為0.45mm。在資金允許的范圍之內(nèi),可通過Matlab仿真得出最外層和內(nèi)層增加的厚度。最優(yōu)設(shè)計(jì)方案如表3所示。熱量分布優(yōu)化如圖7所示。

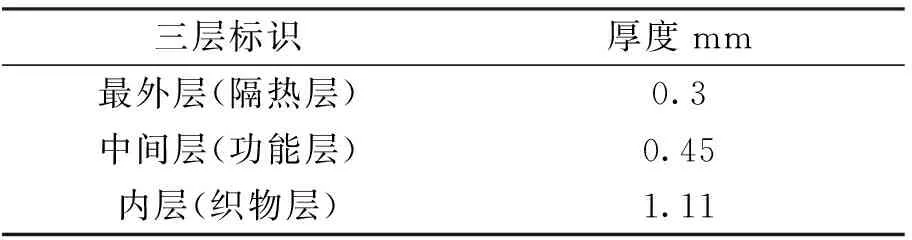
表3 最優(yōu)厚度設(shè)計(jì)方案表

(a) 條件(2)約束下的三維圖

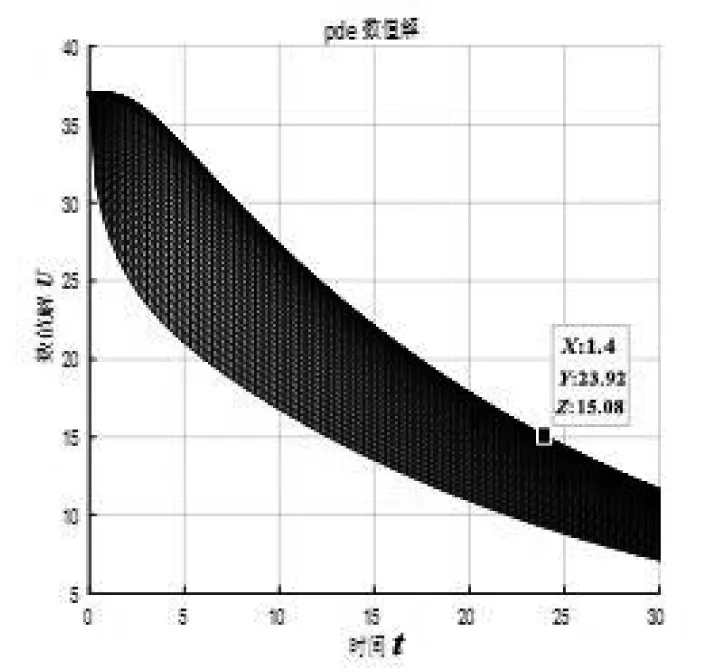
(b) 條件(2)約束下的平面圖圖7 條件(2)約束下的熱量分布優(yōu)化圖

從圖7可以明顯看出,經(jīng)過優(yōu)化設(shè)計(jì)后,在t2=23.92min時(shí)服裝內(nèi)側(cè)溫度降到15℃,與之前相比在低溫環(huán)境站立時(shí)間延長(zhǎng)了6min。

對(duì)于條件(3)而言,在不追加資金情況下,要達(dá)到相同的低溫環(huán)境站立時(shí)間,可以通過提高復(fù)合材料中間層的放熱能力來實(shí)現(xiàn)。利用二分法,基于Matlab進(jìn)行優(yōu)化求解,代碼如下所示。

%% 二分法

function result=dichotomy(fun,x1,x2,eps)

if nargin ～=4

errordlg

elseif fun(x1) * fun(x2)>=0

Errordlg

else

is-eps=(x2-x1)/2;

x=(x2+x1)/2;

while is-eps>=eps

if fun(x)==0

Fprintf

break

elseif fun(x1)*fun(x) < 0

x2=x;

elseif fun(x2)*fun(x) < 0

x1=x;

end

is-eps=(x2-x1)/2;

x=(x2+x1)/2;

end

if is-eps < eps

Fprintf

end

end

通過計(jì)算可以得到k=3,即在外部無風(fēng)、人體靜止時(shí),不改變各層厚度的條件下,需要中間層放熱能力為之前的三倍才能堅(jiān)持23.92min。

通過仿真結(jié)果可以看出,中間層放熱能力為條件(1)的3倍時(shí)才能使其御寒能力與條件(2)相同。條件(2)的優(yōu)化只需要增加一半的成本,帶來的效益卻十分顯著,投資與效益呈正比。條件(3)的優(yōu)化所需成本比較高。

4 結(jié)論

(1)綜合考慮各種傳熱方式和邊界條件,建立了熱傳導(dǎo)模型,并應(yīng)用于低溫防護(hù)服設(shè)計(jì)的優(yōu)化,為滿足不同條件下的實(shí)際需求對(duì)問題進(jìn)行優(yōu)化求解。結(jié)果顯示,建立的數(shù)學(xué)模型符合實(shí)際,具有比較強(qiáng)的通用性和推廣性。

(2)通過Matlab軟件進(jìn)行優(yōu)化求解,簡(jiǎn)單方便,容易實(shí)現(xiàn)。

(3)模型復(fù)雜因素較多,不能對(duì)其進(jìn)行全面的考慮,如由于可行解數(shù)量較少,故采用了遍歷搜索,而遍歷搜索只適用于可行解數(shù)量不大的情況,否則運(yùn)行時(shí)間會(huì)過長(zhǎng)。

本文研究的總體思路、數(shù)學(xué)模型建立與優(yōu)化求解簡(jiǎn)單而且易懂,可以為低溫防護(hù)服的設(shè)計(jì)提供參數(shù)參考與理論依據(jù)。