搜索空間自適應量子搜索算法

謝旭明，段隆振，邱桃榮，康小麗

1(南昌大學 信息工程學院，南昌 330031) 2(南昌大學 圖書館，南昌 330031)

1 引 言

量子計算最早由Feynman[1]提出，此后不少學者提出了不同的量子算法.其中Shor[2]提出的大數質分解量子算法和Grover[3]提出的無序數據庫量子搜索算法是最為經典的兩個量子算法.Shor提出的大數質分解量子算法相對于經典算法實現了多項式級別的加速，但這個算法目前看來只能針對這類特定的問題；而Grover算法，因其解決的搜索問題可應用于許多機器學習算法中，得到了更為廣泛的關注和研究.

Grover算法是由L.K.Grover于1996年提出的.自提出以來，許多學者對其進行了進一步的研究，主要方面有：經典計算下的難點問題、與機器學習相結合、以及算法自身的改進等.

Grover算法能夠處理以前難以解決的或加速需要大量計算的問題.孫國棟等人[4]將Grover算法應用到求根問題上，將求根問題的計算復雜度降低到原來的平方根.朱皖寧等[5]用Grover算法來識別Weblog中的用戶，相較于經典計算，改進策略將搜索的查詢復雜度進行了二次加速.Indranil等[6]先將Grover算法的黑盒添加上動態選擇的功能，然后將改進算法用在推薦系統上.楊婕等[7]先將Grover算法與量子計數相結合，提出一種量子黑箱線路設計方案，然后將提出的方案應用于BLAKE算法的安全性分析中.

Grover算法，因其適用性，也可以用來改進很多機器學習算法的一些子程序，進而達到對原機器學習加速的效果.阮越等[8]將Grover算法引入到主成分分析算法中，設計了一種人臉編碼方案，進一步壓縮了降維處理后的特征空間.Yu等[9]，通過改進Grover算法來求解頻繁項集，實現了關聯規則挖掘的量子化.He等人[10]將經典量子搜索黑盒改進為可以同時接受候選特征集及特征索引的黑盒，實現了特征抽取的量子化.周曉彥等人[11]借助量子搜索的思想對k-means算法進行量子化處理.

為了提高Grover算法的成功概率，不少學者也進行了相關的研究.這方面的研究主要集中在改進算子的相位旋轉角度.Li等[12]將相位角度改為0.1π，Zhong等[13]將相位角度改為1.018，Younes等[14]將相位角度改為1.92684π.這些改進策略使成功概率均獲得了提升.

在已見的Grover算法改進策略中，大多數是圍繞著改變算子的相位角度來進行的，但這些策略的一個致命缺點就是迭代次數不好確定.為解決這個問題，本文提出一種搜索空間自適應的量子搜索算法，擬在不改變迭代次數計算方法的基礎上，提高算法的成功概率.

2 Grover算法及其缺陷

2.1 Grover算法

Grover算法首先要準備n個|0>態的量子位，并通過n個Hadamard門構造一個n量子位的等權重疊加態，然后以一定的次數將U算子作用于n量子位，最后測量這n個量子位.U算子包含兩個子算子Ua和Us：Ua算子又稱為量子黑盒，用于實現目標分量的相位取反；Us算子用于實現目標分量取反后疊加態的均值翻轉.

Grover算法的運算過程在Hilbert空間中的表示如圖1所示.

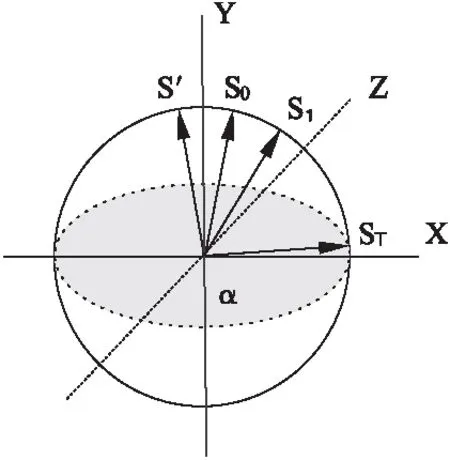
圖1 Grover算法在Hilbert空間的表示Fig.1 Grover algorithm in Hilbert space

圖1中，目標分量值平面α由X軸與Z軸確定.Y軸表示α的垂直分量.s0是初始的等權重疊加態，s′為經過Ua算子作用后的疊加態，s1為s′經過Us算子作用后的疊加態，sT為T次迭代后的疊加態.Grover算法的基本思想就是將與目標分量值平面α夾角較大的疊加態s0經過一系列的幺正變換轉變為與α夾角較小的sT，此時目標分量的概率幅值較大.

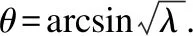
設Tpft是理論上算子的迭代次數，這個值大部分情況下是小數，在現實中是不可能出現小數次的迭代次數的.而T是算法的實際迭代次數，是一個正整數，是對Tpft四舍五入取整后的值.T的表達式如公式(1)所示，其中round()為四舍五入取整函數.Tpft的表達式如式(2)所示.

T=round(Tpft)

(1)

(2)

(3)

2.2 Grover算法的缺陷

結合式(1)-式(3)，成功概率P與目標分量λ的關系可以繪出圖2.

2005年，“北京DRC工業設計創意產業基地”規劃投建，為中國工業設計帶來全新的元素與升級。基地中搭建起“逆向工程實驗室”“3D打印體驗館”“設計博物館”等一系列創意空間；同年，“光華龍騰獎.中國設計十大杰出青年”評選啟動，為中國設計行業發掘中國力量；2006年，“中國設計紅星獎”設立，助力中國設計走出國門，在國際化征途中完成設計服務業和制造業的融合與蛻變；2008年，以北京奧運為契機，“奧運設計”的理念走進社區，走進人們生活，這一年，深圳成為全球第六個世界“設計之都”。

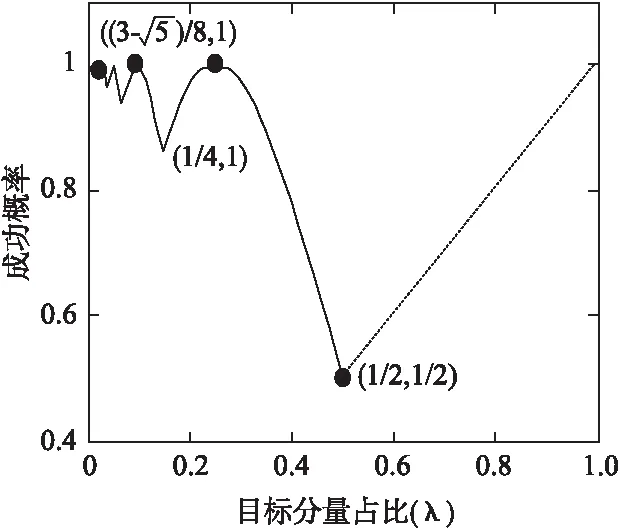
圖2 經典Grover算法成功概率Fig.2 Success rate of the classic Grover algorithm

3 改進的量子搜索算法

當目標分量占比很小的時候，量子搜索算法總能以較高的概率得到目標分量；當目標分量占比較大的時候，算法得到目標分量的概率就不那么高.因此，該研究只需要改進目標分量占比較大的情況.本文擬采用擴大搜索空間的方式來提升目標分量的概率幅.但隨著搜索空間的增大，算法的計算復雜度也會提升，因此，我們必須將搜索空間在合適的范圍內擴大.下面我們先提出幾個定理，再給出具體的改進策略.

3.1 定理證明

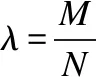
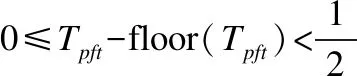
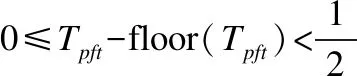
證畢.

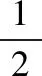
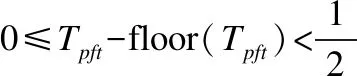
證畢.

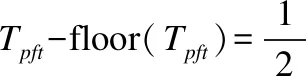
證明：結合定理1和定理2，很容易得出.

證畢.

定理3.當T越大時，目標分量概率的極小值越大.

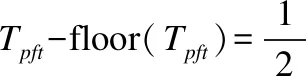
證畢.

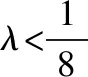
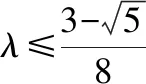
證畢.

3.2 改進策略

(4)

4 算法效率分析

該研究將提出算法與經典Grover算法的效率進行了比較.比較結果如圖3所示.

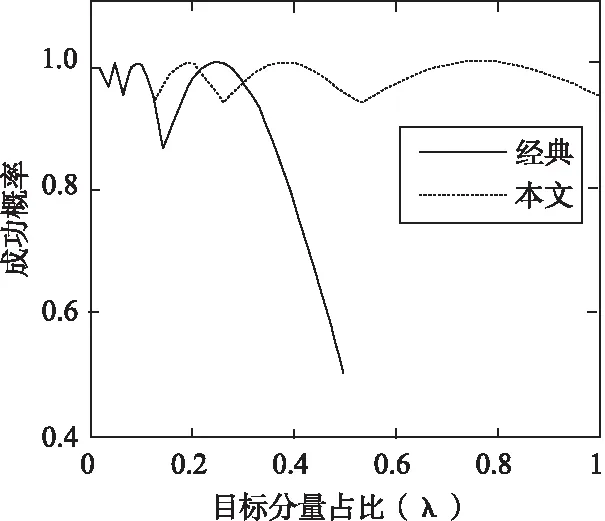
圖3 成功概率比較圖Fig.3 Comparison of success rates

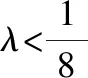
5 結 語

通過自適應地改變不同目標分量占比時的搜索空間，本文整體上實現了成功概率的提升.該策略可以沿用經典Grover算法的思路來求解算子的迭代次數，避免了以往通過改變算子旋轉相位策略的缺陷，在實施方面有更好的可操作性.