冪的運算常見錯誤剖析

文張海華

（作者單位：江蘇省海安市丁所初級中學）

初學冪的運算時，有些同學因為觀察不仔細，對算式的特點沒有辨清就匆忙下筆，出現一些典型錯誤。下面列舉一些，進行剖析，供同學們參考。

例1計算：-m2·（-m）4·（-m）3。

【錯解】-m2·（-m）4·（-m3）=（-m）2+4+3=（-m）9。

【錯因剖析】對底數辨別不清，誤以為三個冪的底數都是-m，就匆忙運用同底數冪相乘的法則，出現了錯誤。

【訂正】原式=-m2·m4·（-m3）=m9。

例2計算：（a2n+1）2。

【錯解】（a2n+1）2=a2n+1×2=a2n+2。

【錯因剖析】當其中一個指數是多項式時，忘了添括號，漏乘。

【訂正】（a2n+1）2=a2（2n+1）=a4n+2。

例3計算：（-x3y）2。

【錯解】（-x3y）2=（-x3）2y2=-x6y2。

【錯因剖析】忘記把“底數”中的系數-1進行平方。

【訂正】（-x3y）2=（-1）2（x3）2y2=x6y2。

例4計算：6a2b÷（-2ab-3）。

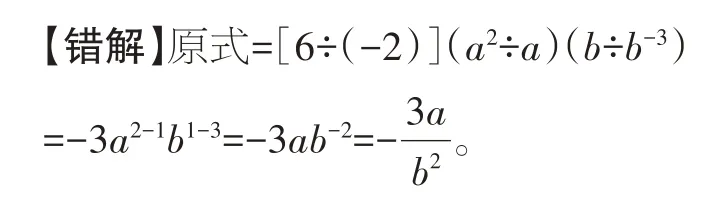
【錯因剖析】b的指數在相減時，應該對指數-3 加上括號，這樣就可得出b的指數為4，而不是-2。

【訂正】原式=6÷（-2）（a2÷a）（b÷b-3）=-3a2-1b1-（-3）=-3ab4。

例5計算：（2x+y）2?（2y+x）?（2x+y）m。

【錯解】原式=（2x+y）2+1+m=（2x+y）3+m。

【錯因剖析】（2x+y）2與（2y+x）不是同底數冪，它們相乘不能用同底數冪的乘法法則。

【訂正】（2x+y）2?（2y+x）?（2x+y）m=（2x+y）2+m（2y+x）。

【小試牛刀】

1.判斷下列計算是否正確？若有錯誤，請改正。

（1）x3?x3=2x3；

（2）x3+x3=x3+3=x6；

（3）（x3）3=x3+3=x6。

2.計算：（-a2）n+（-an）2（n為奇數）。

【參考答案】