大直徑“F”型頂管接口變形安全限值研究
葉冠林, 卞 榮, 張 琪, 潘 上, 林天翔
(1. 上海交通大學(xué)船舶海洋與建筑工程學(xué)院, 上海 200240; 2. 國(guó)網(wǎng)浙江省電力有限公司經(jīng)濟(jì)技術(shù)研究院, 浙江 杭州 310012)
0 引言
現(xiàn)代化城市用電需求巨大,充足穩(wěn)定的電力供應(yīng)是保證生產(chǎn)生活順利進(jìn)行的必要條件。地下電力隧道作為電力傳輸?shù)闹匾ǖ溃淠芊裾9ぷ麝P(guān)系到城市用電安全。近年來(lái)隨著城市的擴(kuò)張和改建,已建電力隧道周邊不斷涌現(xiàn)新工程[1-3]。因此,電力隧道亟需建立相應(yīng)的保護(hù)標(biāo)準(zhǔn)。
與地鐵隧道相比,電力隧道具有以下獨(dú)特性: 1)多采用頂管法施工,最大直徑為4~5 m,小于地鐵隧道。國(guó)內(nèi)新建的電力隧道多為采用“F”型接口的承插式頂管隧道,其轉(zhuǎn)向能力強(qiáng),但整體剛度小,抗擾動(dòng)能力較差[4]。2)內(nèi)部照明條件差加上高壓電纜發(fā)熱引起的高溫(常年30 ℃以上),使得安全隱患難以發(fā)現(xiàn)。這些獨(dú)特性使得電力隧道不宜照搬地鐵隧道的保護(hù)標(biāo)準(zhǔn)。
頂管隧道管節(jié)接口變形安全限值用相鄰管節(jié)之間的最大允許張角和相對(duì)位移(管節(jié)兩端相對(duì)豎向位移)來(lái)表征,最大允許張角的值在頂管隧道的施工階段和使用階段并不相同。國(guó)家規(guī)范(或規(guī)程)[5-6]要求施工階段張角一般不超過(guò)0.3°,若采取額外加固措施也不應(yīng)超過(guò)0.5°; 對(duì)頂管在使用階段的最大允許張角的規(guī)定較少,僅在《給水排水工程頂管技術(shù)規(guī)程》[7]中規(guī)定其不小于0.5°。衛(wèi)珍[8]介紹了玻璃鋼夾砂管雙“F”型接口的結(jié)構(gòu)特點(diǎn),用有限元進(jìn)行接口強(qiáng)度分析,并進(jìn)行了室內(nèi)試驗(yàn); 結(jié)果表明,內(nèi)徑為2.3 m的玻璃鋼夾砂管接口處能承受約1.3°張角而不引起結(jié)構(gòu)破壞,但該研究?jī)H限于特殊的雙“F” 型接口玻璃鋼夾砂管。毛南平[9]從頂管的構(gòu)造出發(fā),提出了使用階段的相鄰管節(jié)位移模式,以及管節(jié)位移引起的接口止水失效類型,并計(jì)算了頂管隧道的允許位移。朱合華等[10]對(duì)上海某內(nèi)徑為2.4 m的鋼筋混凝土頂管施工過(guò)程進(jìn)行了幾何分析和有限元數(shù)值分析,結(jié)果表明采用梁-接口不連續(xù)模型的數(shù)值分析結(jié)果與工程監(jiān)測(cè)值接近。總體而言,既有研究大多依托某一工程實(shí)例,缺乏普遍性; 而且針對(duì)使用階段頂管變形的研究很少。本文研究大直徑(外徑超過(guò)2.0 m)“F”型承插式頂管隧道在正常使用階段不發(fā)生止水失效的變形安全限值,這是因?yàn)榘l(fā)生止水失效破壞要先于結(jié)構(gòu)破壞,是頂管3種破壞(防水、變形、承載力)的第1道防線,有利于保證隧道安全[11-12]。
本文在分析多個(gè)實(shí)際頂管工程案例的基礎(chǔ)上,參考國(guó)家和行業(yè)標(biāo)準(zhǔn),建立相鄰管節(jié)位移幾何關(guān)系,分析管節(jié)允許最大張角及位移,以期為電力頂管隧道保護(hù)標(biāo)準(zhǔn)的制定提供參考。
1 典型電力頂管隧道設(shè)計(jì)參數(shù)統(tǒng)計(jì)
通過(guò)對(duì)福建、江西、浙江3個(gè)電力勘察設(shè)計(jì)院頂管工程設(shè)計(jì)實(shí)例細(xì)部尺寸進(jìn)行調(diào)研發(fā)現(xiàn): 外徑超過(guò)2.4 m的大直徑頂管隧道管節(jié)間均采用“F”型承插口,管節(jié)外徑為2.4~4.14 m,徑厚比為11~12; 頂管前節(jié)管節(jié)尾端(承口)設(shè)鋼套筒,后節(jié)管節(jié)前端(插口)根據(jù)工程需要設(shè)置1~2道楔形橡膠圈。代表性工程及相關(guān)參數(shù)見表1—3。

表1 福建省電力勘測(cè)設(shè)計(jì)研究院工程實(shí)例

表2 江西省電力勘測(cè)設(shè)計(jì)研究院工程實(shí)例
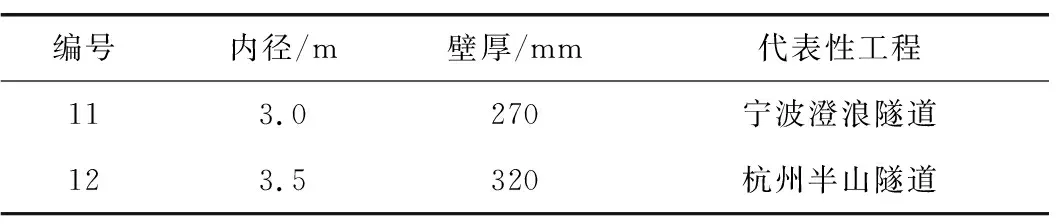
表3 浙江省電力勘測(cè)設(shè)計(jì)研究院工程實(shí)例
2 承插式頂管接口構(gòu)造與破壞模式
頂管隧道通常由相同長(zhǎng)度的預(yù)制管節(jié)承接而成。預(yù)制管節(jié)本身剛度較大,但相鄰兩管節(jié)接口處剛度較小,接口止水失效會(huì)先于結(jié)構(gòu)性破壞發(fā)生,并且由于在隧道中鋪設(shè)有電纜管線,對(duì)接口處抗?jié)B漏性要求較高。采用單圈與雙圈橡膠止水的頂管接口處構(gòu)造有所不同,接口構(gòu)造詳圖分別如圖1和圖2所示。
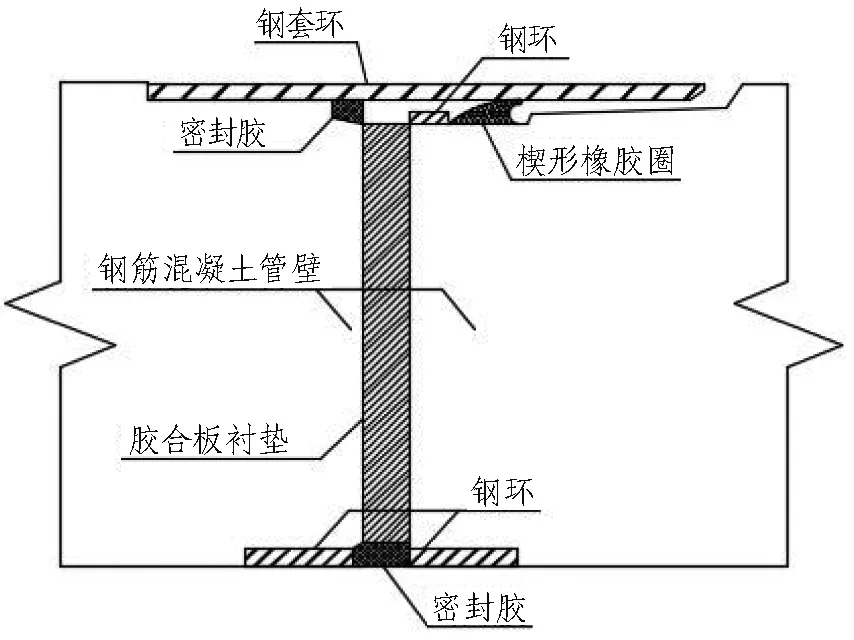
圖1 單圈橡膠止水頂管隧道接口處構(gòu)造詳圖

1—5為止水失效關(guān)鍵點(diǎn)。
近年來(lái)有多處頂管隧道受鄰近施工影響導(dǎo)致破壞的案例。例如: 福建某電力頂管隧道受鄰近堆載擾動(dòng)影響,導(dǎo)致隧道局部隆起,引發(fā)該段隧道不同程度的漏水和結(jié)構(gòu)性破壞; 武漢某電力隧道受鄰近高架橋樁基施工影響,導(dǎo)致隧道發(fā)生滲漏,內(nèi)部嚴(yán)重積水; 重慶某電力隧道受地表堆載和降雨影響,發(fā)生局部沉降,導(dǎo)致結(jié)構(gòu)性破壞。調(diào)研發(fā)現(xiàn),隨著頂管隧道發(fā)生不同程度變形,漏水最先發(fā)生在管節(jié)接口處,且漏水處的楔形橡膠圈均有不同程度的損壞或松弛情況。位于重慶的受損電力隧道有一部分裸露在地表,還能觀察到鋼套環(huán)與鋼筋混凝土管壁擠壓碰撞導(dǎo)致密封性喪失,進(jìn)而發(fā)生漏水。
結(jié)合以上調(diào)研情況和以往工程經(jīng)驗(yàn),將頂管管節(jié)接口處止水失效的關(guān)鍵點(diǎn)歸納為如圖2所示的5處(點(diǎn)1—5),并總結(jié)接口止水失效原因,主要有以下4種:
1)接口處承管鋼套環(huán)與接管鋼筋混凝土管壁擠壓破壞,接觸點(diǎn)為圖2中點(diǎn)5。本研究不考慮鋼套環(huán)與鋼筋混凝土管壁的彈塑性,認(rèn)為二者一接觸即破壞,這樣的結(jié)果是偏于安全的。
2)2道止水橡膠帶均失效引起滲漏。包括2種失效類型,第1種是橡膠被擠壓過(guò)度導(dǎo)致失效,接觸點(diǎn)可以認(rèn)為是圖2中點(diǎn)1、點(diǎn)3; 第2種是鋼套環(huán)與橡膠止水帶脫離或松弛,導(dǎo)致對(duì)橡膠的壓力低于頂管周圍靜水壓力而發(fā)生滲漏,失效點(diǎn)為圖2中點(diǎn)2、點(diǎn)4。
3)接口的承管與接管脫開,導(dǎo)致止水環(huán)脫出鋼套環(huán)保護(hù)范圍引起大量滲漏。
4)前后管節(jié)間壓力過(guò)大將襯墊過(guò)度壓縮破壞。這種失效類型發(fā)生的可能性較低并且是可控的,因?yàn)橐r墊被2道橡膠止水保護(hù)在內(nèi)部,很難先于橡膠、鋼套環(huán)破壞,且襯墊的材料與厚度均有較大自主調(diào)節(jié)性。因此,本文主要考慮前3點(diǎn)破壞原因。
頂管隧道的變形分為管節(jié)之間相對(duì)位移和管節(jié)自身變形。如前文所述,頂管通常都是預(yù)制的,管節(jié)的剛度遠(yuǎn)大于連接處剛度,可視為剛體,管身結(jié)構(gòu)性開裂導(dǎo)致的漏水不會(huì)先于接口處止水失效導(dǎo)致的漏水發(fā)生。對(duì)于頂管管節(jié)之間的相對(duì)位移,考慮到接口不是對(duì)稱的,因此按照剛性管進(jìn)行分析,可能的位移模式共有6種,如圖3所示。
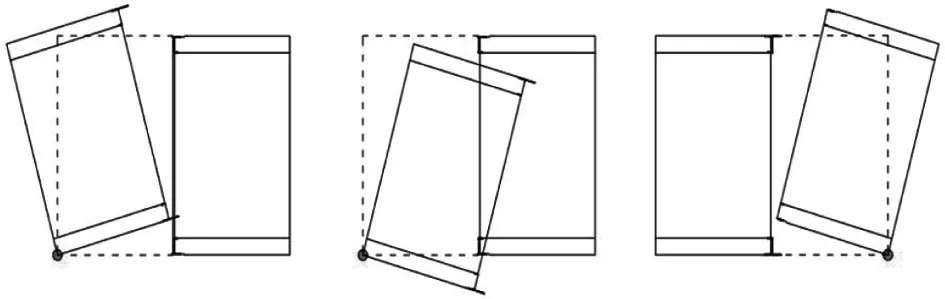
(a) 模式1 (b) 模式2 (c) 模式3
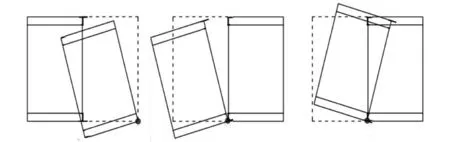
(d) 模式4 (e) 模式5 (f) 模式6
工程經(jīng)驗(yàn)表明,前4種相對(duì)位移模式多出現(xiàn)在頂管施工階段機(jī)頭段,使用階段可能發(fā)生的位移模式為后2種,即模式5和模式6。考慮到頂管管節(jié)接口在不采取焊接等加固措施時(shí),接口處不能承受拉力,而鋼筋混凝土管壁具有一定的承壓能力,可以認(rèn)為模式5引起漏水的概率相較于模式6要高。因此,本文選取位移模式5進(jìn)行分析,建立張角與結(jié)構(gòu)細(xì)部尺寸之間的幾何關(guān)系式。
3 “F”型接口變形安全限值研究
3.1 相鄰管節(jié)允許張角
以“F”型雙圈止水為例,分析頂管隧道管節(jié)間張角的允許值。在位移模式5中,顯然內(nèi)圈橡膠失效發(fā)生在外圈之后,單、雙圈止水的計(jì)算本質(zhì)相同,只是尺寸有區(qū)別。雙圈止水構(gòu)造的頂管工程以杭州半山頂管工程為例,頂管管節(jié)接口處尺寸如圖4所示(單圈止水構(gòu)造類似),頂管壁厚320 mm,單節(jié)標(biāo)準(zhǔn)管節(jié)長(zhǎng)度l=2.5 m,內(nèi)徑d=3.5 m,外徑D=4.14 m,鋼套環(huán)外伸有效長(zhǎng)度a1=240 mm,2道橡膠止水環(huán)厚度均為16 mm,與接口距離分別為a3=100 mm、a2=165 mm,鋼套環(huán)與鋼筋混凝土管壁空隙h1=5 mm。可以假設(shè)2道止水都失效為接口破壞標(biāo)準(zhǔn),因此外圈止水位置a2不影響破壞模式,詳見下面計(jì)算。
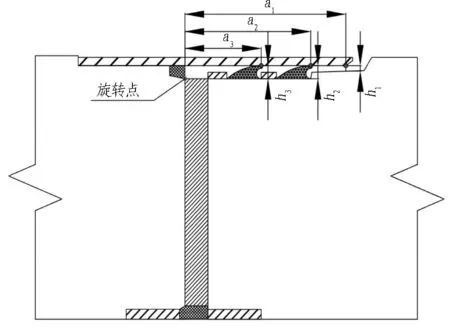
圖4 “F”型接口關(guān)鍵尺寸詳圖
3.1.1 位移控制指標(biāo)
1)承管鋼套環(huán)最外緣與接管管身豎向位移值h1=5 mm。從安全角度考慮,認(rèn)為鋼套環(huán)與混凝土管壁接觸為破壞值。對(duì)于采用其他管徑的隧道,為了便于承接和保證密封性,預(yù)留的空間基本相同,都為5~6 mm,與文獻(xiàn)[13]一樣,取5 mm作為控制指標(biāo)。
2)橡膠止水帶材料多采用三元乙丙橡膠(EPDM)、丁腈橡膠(NBR)或氯丁橡膠(CR)進(jìn)行制作,根據(jù)國(guó)際標(biāo)準(zhǔn)[14],橡膠止水帶可壓縮量不宜大于50%厚度。管節(jié)承接前橡膠止水帶厚度為26 mm,承接后被壓縮至16 mm,因此:
①使用階段的剩余允許壓縮量為26 mm×50%-(26 mm-16 mm)=3 mm,以此作為橡膠止水帶被壓壞而失去耐久性的位移控制指標(biāo)。
②使用階段允許松弛量為3 mm,以此作為橡膠止水帶壓力不足導(dǎo)致地下水滲入的位移控制指標(biāo)。毛南平[9]以工程經(jīng)驗(yàn)取該值為4 mm; 本文研究人員對(duì)浙江、湖南、福建、湖北等地工程實(shí)例進(jìn)行了調(diào)研,認(rèn)為地下水位對(duì)會(huì)對(duì)該值產(chǎn)生影響,與高海東等[15]通過(guò)數(shù)值模擬計(jì)算得到的結(jié)論一致。對(duì)江浙滬等地下水位較高的區(qū)域,建議取3 mm為松弛限值,使結(jié)果安全可靠。
3)鋼套環(huán)水平位移量達(dá)到a1-a3=145 mm,以此作為橡膠止水帶脫離鋼套環(huán)的位移控制指標(biāo)。
3.1.2 雙圈止水頂管止水失效算例
管節(jié)繞承管與襯墊最外邊緣交點(diǎn)旋轉(zhuǎn),旋轉(zhuǎn)引起的張角逐漸增大,兩端接口發(fā)生分化,一端(接口1)最松弛,另一端(接口2)則壓至最緊密,中部的變形介于兩者之間。本文以接口1和接口2為代表的極端變形進(jìn)行分析,如圖5所示。
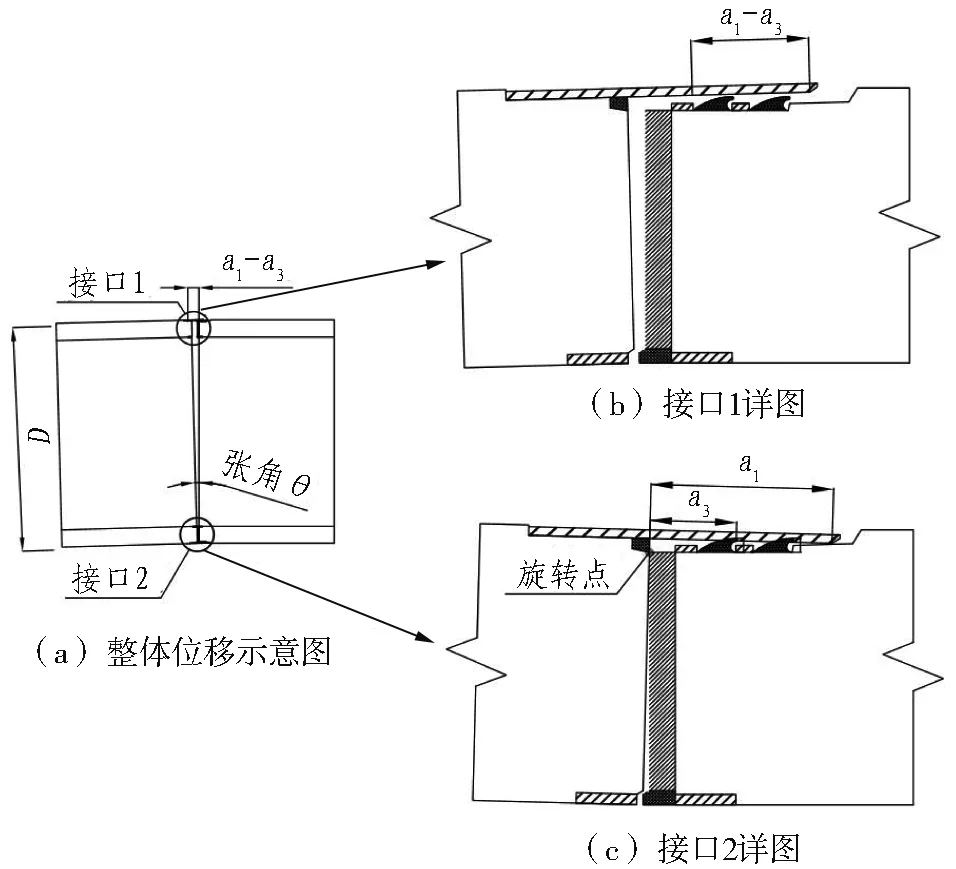
圖5 位移模式5計(jì)算示意圖
1)接口1處橡膠止水帶“脫離”失效。“脫離”指相鄰管節(jié)轉(zhuǎn)動(dòng)過(guò)程中,鋼套環(huán)末端與內(nèi)圈(靠近接口)橡膠的水平位移達(dá)到a1-a3,此時(shí)2道止水橡膠均脫離了鋼套環(huán)的保護(hù)范圍,導(dǎo)致止水失效。算式為
(1)
即
(2)
將a1=245 mm、a3=100 mm、D=4 140 mm代入式(2),得到張角θ≥2.007°。
2)橡膠止水帶“松弛”失效計(jì)算。“松弛”是指鋼套環(huán)與內(nèi)圈橡膠接觸點(diǎn)豎向位移達(dá)到3 mm控制指標(biāo),此時(shí)2道止水橡膠密封性低于抗?jié)B要求,認(rèn)為發(fā)生止水失效破壞,如圖6所示。算式如下:
(a3+Dθ)sinθ≥3 mm 。
(3)
由于θ很小,可近似為θ=sinθ,式(3)變?yōu)椋?/p>
(a3+Dθ)θ≥3 mm 。
(4)
將a3=100 mm、D=4 140 mm代入式(4)并解該一元二次方程,得θ≥0.017 4 rad=0.998°或θ≤-0.041 5 rad=-2.38°,將負(fù)值舍棄便得到張角θ≥0.998°。

圖6 接口1止水松弛計(jì)算示意圖
3)鋼套環(huán)與混凝土接觸失效計(jì)算見圖5(c),可得到算式
a1·sinθ≥5 mm 。
(5)
即
(6)
將a1=245 mm代入式(6),得到張角θ≥1.169°。
4)橡膠止水帶擠壓失效計(jì)算見圖5(c),此時(shí)a3起控制作用,算式為
a3·sinθ≥3 mm 。
(7)
即
(8)
將a3=100 mm代入式(8),得到張角θ≥1.719°。
由式(1)和式(2)可知,橡膠止水松弛發(fā)生在鋼套環(huán)脫離失效之前; 由式(3)和式(4)可知,鋼套環(huán)與鋼筋混凝土管壁接觸失效要先于止水橡膠擠壓破壞發(fā)生。下節(jié)的計(jì)算表明,松弛端必先于壓密端失效,與管徑無(wú)關(guān),但具體是“松弛”還是“脫離”失效與管徑有關(guān)。
采用單圈止水構(gòu)造的頂管工程實(shí)例細(xì)部尺寸略有不同,統(tǒng)計(jì)如表4所示; 采用雙圈止水構(gòu)造的頂管在位移模式5下的內(nèi)圈止水橡膠要后于外圈止水橡膠失效,起控制作用的是a3的值。因此,雙圈和單圈止水構(gòu)造頂管的計(jì)算本質(zhì)上是相同的,都只用了1圈的參數(shù),均可用式(1)—(8)進(jìn)行計(jì)算。

表4 采用單圈橡膠止水的實(shí)際工程關(guān)鍵參數(shù)統(tǒng)計(jì)
將表4中工程實(shí)例對(duì)應(yīng)張角全部計(jì)算出來(lái)并取最大值,結(jié)果如表5所示。由表可知,以上頂管工程實(shí)例的止水失效類型均發(fā)生在脫離側(cè)(接口1),具體表現(xiàn)為鋼套環(huán)脫離或止水橡膠松弛; 并且隨著管徑增大,失效張角整體呈現(xiàn)減小趨勢(shì),但均滿足規(guī)程[7]中第4.3.9條第4點(diǎn)關(guān)于鋼筋混凝土管“接口的允許偏轉(zhuǎn)角應(yīng)大于0.5°”的規(guī)定。為便于建立統(tǒng)一的控制標(biāo)準(zhǔn),建議將失效張角中的最小值0.844°進(jìn)一步取0.8°作為管節(jié)不發(fā)生滲漏時(shí)的允許張角,這樣的結(jié)果是足夠安全的。
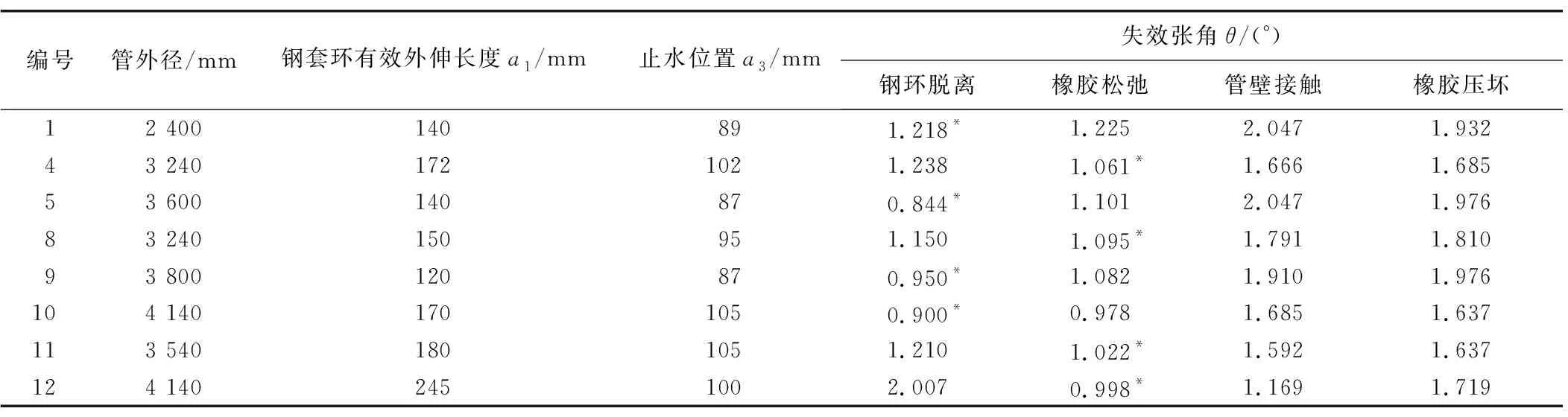
表5 各院頂管工程失效張角計(jì)算
3.2 單節(jié)管允許相對(duì)位移
目前工程上大口徑鋼筋混凝土頂管的單節(jié)管長(zhǎng)最常采用2.0 m和2.5 m[16],在轉(zhuǎn)角或頂進(jìn)的首尾段有時(shí)也會(huì)使用少量其他長(zhǎng)度(1.0、1.5、3.0 m)的管節(jié)配合施工。表5中除10號(hào)采用的是2.0 m管長(zhǎng)以外,其余工程均采用2.5 m管長(zhǎng)。以2.5 m單節(jié)管長(zhǎng)為例,1對(duì)承接管長(zhǎng)度為2×2.5 m=5 m,這個(gè)尺度遠(yuǎn)小于受到鄰近堆載、樁基施工和基坑開挖等工況對(duì)土體的影響范圍(以土體變形達(dá)到5 mm為界)。因此,可以近似地認(rèn)為土體位移最大處2個(gè)相接管節(jié)的變形是對(duì)稱的,其中單節(jié)管兩端相對(duì)位移與節(jié)間張角關(guān)系為ΔL=la=l·θ/2,水平張開量計(jì)算公式為ΔH=Dθ,如圖7所示。

圖7 頂管管節(jié)張角與相對(duì)位移的定義
工程實(shí)際應(yīng)用中,頂管隧道的沉降相較于水平張開量更易于測(cè)量,故以單節(jié)管旋轉(zhuǎn)對(duì)應(yīng)的遠(yuǎn)端最大相對(duì)位移作為允許相對(duì)位移,和允許張角一起用于表征頂管的變形安全限值。
表6示出不同管長(zhǎng)頂管隧道變形安全限值匯總。對(duì)于后續(xù)新建工程,若采用不同管徑、管長(zhǎng)參數(shù),仍可通過(guò)式(1)—(8)計(jì)算。但還應(yīng)考慮到將此研究結(jié)果應(yīng)用到工程實(shí)際中時(shí),若對(duì)每種管徑都要進(jìn)行1次計(jì)算,既不利于統(tǒng)一標(biāo)準(zhǔn)的建立,又會(huì)增加現(xiàn)場(chǎng)施工、監(jiān)測(cè)人員的工作強(qiáng)度,因此,建議將表6中相對(duì)位移的最小值(15.7 mm)進(jìn)一步取15 mm,作為大直徑電力頂管隧道在2.0 m和2.5 m單節(jié)管長(zhǎng)條件下統(tǒng)一的位移允許限值,這樣的結(jié)果也是偏于安全的。頂管外徑與允許相對(duì)位移關(guān)系見圖8,由圖可知,相同管長(zhǎng)條件下,頂管外徑與允許相對(duì)位移呈一定的負(fù)相關(guān)性; 而根據(jù)ΔL=la可知,管長(zhǎng)與相對(duì)位移呈正比關(guān)系。
應(yīng)注意的是,上述計(jì)算分析結(jié)果實(shí)際針對(duì)的是在施工階段采用直線頂進(jìn)的頂管部分,這種條件下頂管投入使用后,在不考慮施工偏差的情況下,管節(jié)之間沒有初始張角; 但實(shí)際頂管工程在推進(jìn)時(shí),經(jīng)常存在需要通過(guò)曲線頂進(jìn)來(lái)繞過(guò)某些障礙物的情況。施工階段采用曲線頂進(jìn)的頂管在投入使用后,管節(jié)之間存在初始張角,初始張角的存在實(shí)際擠占了允許張角的空間,也直接影響允許相對(duì)位移余量。

表6 不同管長(zhǎng)頂管隧道變形安全限值匯總
頂管工程施工頂進(jìn)階段的允許張角要小于正常使用階段管節(jié)的允許張角,文獻(xiàn)[5]和文獻(xiàn)[6]均規(guī)定曲線頂進(jìn)施工時(shí),相鄰兩管節(jié)之間的張角宜小于0.3°; 而文獻(xiàn)[7]中規(guī)定使用階段的管節(jié)允許張角應(yīng)不小于0.5°,考慮到電力管廊防水要求較給排水管廊更高,電力頂管管節(jié)在使用階段的允許張角還應(yīng)在0.5°的基礎(chǔ)上提高。圖9示出典型頂管工程外徑與允許張角的關(guān)系,結(jié)果表明二者同樣呈現(xiàn)一定的負(fù)相關(guān)性,并且各典型工程的管節(jié)允許張角均大于0.5°,符合文獻(xiàn)[7]的要求,這也從側(cè)面驗(yàn)證了本文研究成果的可靠性。
4 工程案例分析
成都市某電力頂管隧道于2012年投入使用,該段頂管外徑為2.4 m,管節(jié)長(zhǎng)度為2.0 m。2013年成都地鐵某線二期施工后,由于受地鐵施工擾動(dòng),該段頂管隧道部分頂管管節(jié)接口處受損,發(fā)生隧道開裂滲漏事故。

黑色填充為典型工程的采用值。
在事故發(fā)生之后,維運(yùn)人員對(duì)該段隧道管節(jié)滲漏、變形情況進(jìn)行檢測(cè),發(fā)現(xiàn)頂管隧道接縫處出現(xiàn)了大量滲水點(diǎn),這些滲水點(diǎn)是管節(jié)接口產(chǎn)生張角引起的。根據(jù)檢測(cè)結(jié)果,將發(fā)生滲水頂管管節(jié)接口張角值匯總見表7。由第3節(jié)得到的結(jié)論可知,對(duì)于該幾何尺寸的頂管隧道,頂管發(fā)生滲水情況時(shí)允許張角為0.8°; 由表7可知,該工程案例中頂管隧道發(fā)生點(diǎn)滲時(shí)管節(jié)接口最小張角為1.5°,超過(guò)允許張角值。因此,可以表明本文得出的研究結(jié)論是可靠且偏于安全的。
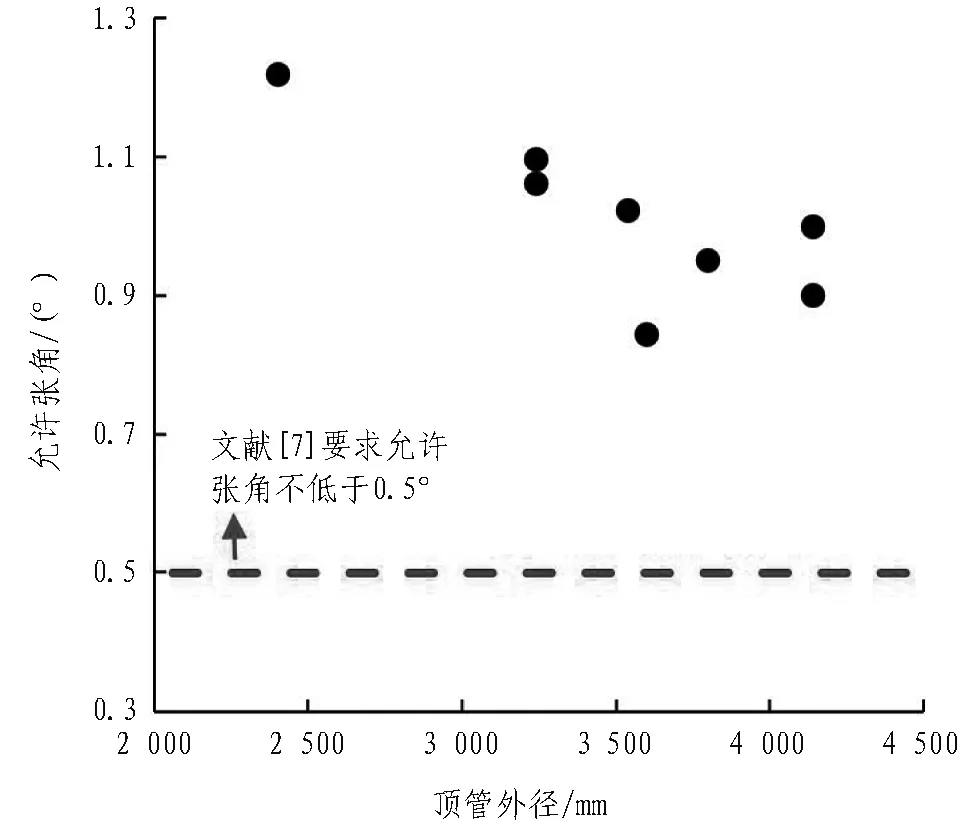
圖9 典型頂管工程外徑與允許張角關(guān)系
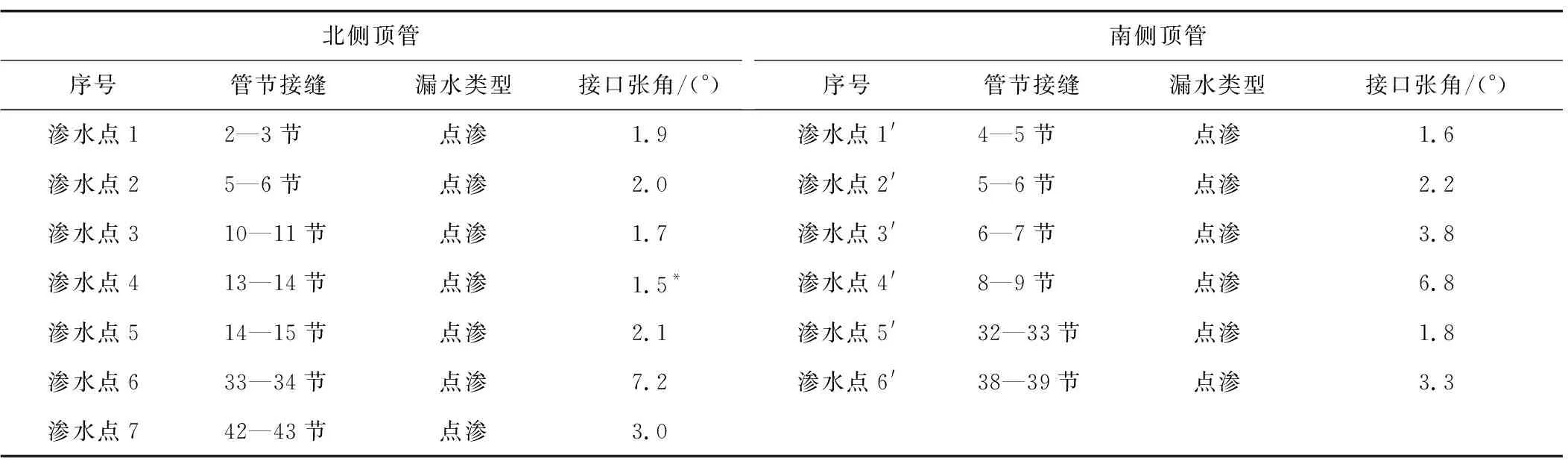
表7 成都市某電力頂管隧道受鄰近施工擾動(dòng)變形情況
5 結(jié)論與討論
針對(duì)大直徑“F”型承插式頂管在使用階段的變形安全限值問(wèn)題,本文開展了工程案例統(tǒng)計(jì)分析和理論計(jì)算,所得成果在具體工程事故中得到驗(yàn)證,以期為制定頂管隧道保護(hù)標(biāo)準(zhǔn)提供參考。主要結(jié)論如下:
1)管節(jié)接口止水失效主要有2種: ①橡膠止水帶與鋼套環(huán)脫離失效; ②橡膠止水帶與鋼套環(huán)和鋼筋混凝土管壁接觸壓力低于防滲要求。二者的發(fā)生順序受頂管管徑影響。
2)管節(jié)允許張角和允許相對(duì)位移均與管徑呈一定的負(fù)相關(guān)性,同時(shí),管節(jié)允許相對(duì)位移還受管長(zhǎng)影響(二者呈正比關(guān)系)。
3)接口變形安全限值包括最大張角和相對(duì)位移,建議統(tǒng)一以0.8°作為允許張角,以15 mm為2.0、2.5 m管長(zhǎng)的允許相對(duì)位移。上述取值安全合理,且便于在電力頂管隧道的保護(hù)工程中執(zhí)行。
4)若頂管隧道存在因曲線頂進(jìn)的初始彎曲變形,還應(yīng)從總允許變形中減去初始變形,得到該頂管隧道實(shí)際允許變形量。
本文的研究對(duì)象主要是“F”型承插接口的混凝土頂管隧道,以管節(jié)之間的幾何關(guān)系在最不利情況下提出了相應(yīng)的變形安全限值。后續(xù)可針對(duì)其他接口形式、材料的頂管隧道變形安全限值和結(jié)構(gòu)受力變形特性進(jìn)行進(jìn)一步探討與研究。
參考文獻(xiàn)(References):
[1] 汪從敏, 程國(guó)開, 王志勇, 等. 新建隧道對(duì)既有電纜隧道的影響規(guī)律及保護(hù)區(qū)范圍分析[J]. 地下工程與隧道, 2016(3): 15.
WANG Congmin, CHENG Guokai, WANG Zhiyong, et al. Influence rule of new tunnel on existing cable tunnel and protection scope[J]. Underground Engineering and Tunnels, 2016(3): 15.
[2] PELLET B A L, KASTNER R. Experimental and analytical study of friction forces during microtunneling operations[J]. Tunnelling and Underground Space Technology, 2002, 17 (1): 83.
[3] 況龍川, 李智敏, 殷宗澤. 地下工程施工影響地鐵隧道的實(shí)測(cè)分析[J]. 清華大學(xué)學(xué)報(bào)(自然科學(xué)版), 2000, 40(增刊1): 79.
KUANG Longchuan, LI Zhimin, YIN Zongze. Analysis of field measurement data on responses of metro tunnel due to substructure construction[J]. Journal of Tsinghua University (Science and Technology), 2000, 40(S1): 79.
[4] 丁文其, 袁森林, 高小慶, 等. 電力隧道超大直徑頂管施工擾動(dòng)特性研究[J]. 巖土力學(xué), 2010, 31(9): 2901.
DING Wenqi, YUAN Senlin, GAO Xiaoqing, et al. Research on construction disturbance characteristics caused by super large diameter pipe jacking in electric power tunnel[J]. Rock and Soil Mechanics, 2010, 31(9): 2901.
[5] 給水排水管道工程施工及驗(yàn)收規(guī)范: GB 50268—2008[S]. 北京: 中國(guó)建筑工業(yè)出版社, 2008.
Code for construction and acceptance of water and sewerage pipeline works: GB 50268-2008[S]. Beijing: China Architecture and Building Press, 2008.
[6] 中國(guó)非開挖技術(shù)協(xié)會(huì). 頂管施工技術(shù)及驗(yàn)收規(guī)范(試行)[S]. 武漢: 中國(guó)地質(zhì)大學(xué)出版社, 2006.
CSTT. Specifications for construction and acceptance of pipe jacking[S]. Wuhan: China University of Geosciences Press, 2006.
[7] 給水排水工程頂管技術(shù)規(guī)程: CECS 246: 2008[S]. 北京: 中國(guó)建筑工業(yè)出版社, 2008.
Technical specification for pipe jacking of water supply and sewerage engineering: CECS 246: 2008[S]. Beijing: China Architecture and Building Press, 2008.
[8] 衛(wèi)珍. 新型接口在玻璃鋼夾砂管頂管工程中的運(yùn)用[J]. 中國(guó)市政工程, 2008(6): 45.
WE Zhen. Application of new joints to pipejacking of sand-sandwiched GRP pipes[J]. China Municipal Engineering, 2008 (6): 45.
[9] 毛南平. 頂管電力隧道保護(hù)值的分析研究[J]. 地下工程與隧道, 2015(4): 29.
MAO Nanping. Study on protection value of power tunnel with pipe jacking[J]. Underground Engineering and Tunnels, 2015(4): 29.
[10] 朱合華, 葉冠林, 潘同燕. 大口徑急曲線鋼筋混凝土頂管管節(jié)接縫張開量分析[J]. 施工技術(shù), 2001, 30(1): 36.
ZHU Hehua, YE Guanlin, PAN Tongyan. Analysis of splaying amount of joints of segments of large-diameter large-curvature reinforcement concrete pushing-pipe [J]. Construction Technology, 2001, 30(1): 36.
[11] 劉浩, 肖武權(quán), 冷伍明. 既有隧道上方新建高層建筑對(duì)其影響的監(jiān)測(cè)分析[J]. 隧道建設(shè), 2008, 28(4): 434.
LIU Hao, XIAO Wuquan, LENG Wuming. Monitoring and analysis on influence of high-rise building construction on existing underneath tunnel[J]. Tunnel Construction, 2008, 28(4): 434.
[12] 何川, 劉川昆, 王士民, 等. 裂縫數(shù)量對(duì)盾構(gòu)隧道管片結(jié)構(gòu)力學(xué)性能的影響[J]. 中國(guó)公路學(xué)報(bào), 2018, 31(10): 210.
HE Chuan, LIU Chuankun, WANG Shimin, et al. Influence of crack number on mechanical properties of shield tunnel segment structure[J]. China Journal of Highway and Transport, 2018, 31(10): 210.
[13] 張鵬, 曾聰, 王道偉, 等. 拱北隧道曲線鋼頂管接頭橡膠圈結(jié)構(gòu)數(shù)值模擬研究[J]. 隧道建設(shè), 2016, 36(10): 1226.
ZHANG Peng, ZENG Cong, WANG Daowei, et al. Study of numerical simulation of rubber ring of curved steel pipe jacking joints of Gongbei tunnel [J]. Tunnel Construction, 2016, 36(10): 1226.
[14] Elastomeric seals-material requirements for pipe joint seals used in water and drainage applications (Part 1: Vulcanized rubber): AS 681.1-2008[S]. Australia: Committee WS-010, 2008.
[15] 高海東, 趙濤, 馬勝利, 等. 高水壓條件下鋼頂管管節(jié)密封性試驗(yàn)及數(shù)值模擬研究[J]. 現(xiàn)代隧道技術(shù), 2015, 52(2): 148.
GAO Haidong, ZHAO Tao, MA Shengli, et al. Sealing test and numerical simulation for steel jacking pipe joint under high water pressure [J]. Modern Tunnelling Technology, 2015, 52(2): 148.
[16] SOFIANOS A L, LOUKAS P, CHANTZAKOS C. Pipe jacking a sewer under Athens[J]. Tunnelling and Underground Space Technology, 2004, 19(2): 193.

