基于ADAMS和ANSYS Workbench的AGV剪叉式升降機構的仿真分析研究

徐恒才， 李鷺揚

（揚州大學 機械工程學院，江蘇 揚州225127）

0 引言

隨著科技的不斷發展，AGV開始廣泛應用于各領域，提升機構作為AGV不可或缺的一部分，發揮著極其重要的作用。提升機構與AGV是一個整體結構，所以對提升機構的尺寸和穩定性有所要求。現有機構中，AGV提升機構普遍具有結構復雜、自身質量較大、穩定性弱等缺點，為了解決這些問題，剪叉提升機構開始進入人們的視野[1]，但是一些剪叉式的提升機構在提升的時候載物板的重心會發生偏移，向一端轉移，因此不適合質量分布不均的載物場合；還有一些剪式提升機構中雖然解決了重心偏移的問題，但是驅動單元是伴隨提升機構升降的，這就意味著升降機構在舉升的同時還要承載電動機的重力，并且電動機隨升降機構升降就意味著電動機的線路也要隨之上下運動，這樣對電路損壞極大；提升機構的驅動單元采用液壓或者電缸，這就導致提升機構會比較大、比較笨重，從而導致AGV整體尺寸變大，不適合在AGV上應用；其他一些提升機構結構復雜，不便于后期維護。

針對以上問題，設計了一種剪叉式AGV提升機構，包括固定底板、兩個升降組件、升降板和驅動部件，解決了結構復雜不可靠的技術難題，結構簡單，工作可靠，具有廣闊的市場優勢和前景。本文利用SolidWorks軟件進行參數建模，并通過仿真軟件ADAMS和ANSYS Workbench進行虛擬仿真分析，得到相關技術參數，為產品設計和優化提供參考和數據支持[2]。

1 仿真虛擬樣機的建立

1.1 模型建立與簡化

本研究設計的AGV剪叉式升降機構的基本參數如下：舉升托板尺寸為500 mm×300 mm，提升高度行程至少為80 mm，剪支桿長為200 mm，采用SolidWorks軟件建立模型。將舉升托板的上表面至車架底板的上表面的距離調至140 mm，將裝配好的三維模型導入到ADAMS中。

1.2 定義特征

將簡化之后的機構，絲桿螺母的材料定義為軸承鋼，密度為7.81 g/cm3，其它材料全部設置為鋁合金，密度為2.74 g/cm3。AGV最大負載為100 kg，定義整個環境為理想狀態，在舉升托板的幾何中心施加一個豎直向下100 kg的載荷。利用布爾和操作將車架底板、升降組件、滑軌組件、升降托板合為一體，然后根據實際運動狀態添加相應的運動副及約束。

圖1 升降機構三維模型圖

2 剪叉升降機構仿真分析

2.1 升降機構絲桿螺母和托板運動學仿真分析

2.1.1 添加驅動

定義仿真的剪叉式升降機構托板上升和下降過程的行程至少為80 mm，為了更好地模擬仿真其運動過程，定義升降托板運動過程為：0～1 s加速，1～4 s勻速，4～5 s減速，最大速度即勻速階段設置為20 mm/s，整個上升過程時間為5 s，現對托板升起過程進行運動學仿真分析，設置運動函數為

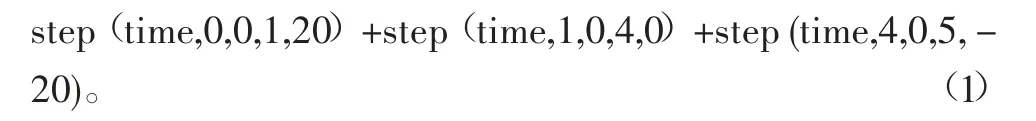
2.1.2 仿真分析

運行仿真使升降機構上升到工作高度并停止，得仿真變化曲線圖，如圖2～圖5所示。

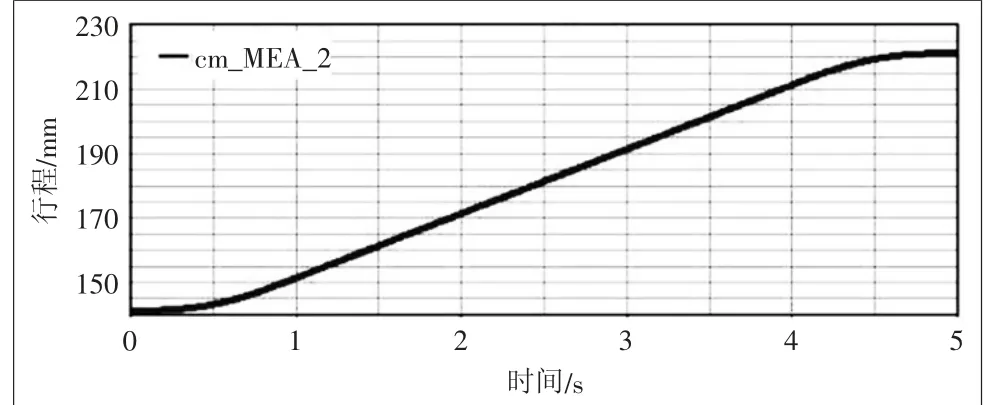
圖2 升降托板行程

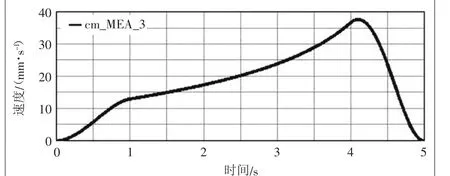
圖4 升降機構絲桿螺母前進速度變化曲線

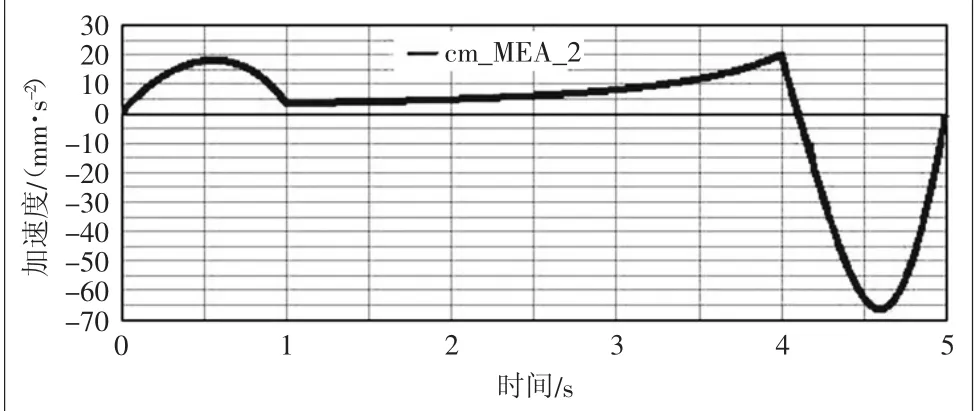
圖5 升降機構絲桿螺母運動加速度變化曲線

從圖2中得出托板的運行高度軌跡為141.4545～221.4545 mm，行程為80 mm，符合設計要求。從圖4可以看出，升降機構在運行過程中絲桿螺母帶動推桿前進的速度不斷增加，在4.1 s左右達到峰值37.7043 mm/s，結合圖5加速度曲線圖可以看出，在0～4 s之間（即加速和勻速階段），螺母最大加速度為20.2167 mm/s2，4～5 s減速階段達到減速峰值66.2602 mm/s2，符合實際工況。

此仿真得到了升降機構絲桿的轉速，進而可以得到電動機所需的轉速，最終得到升降機構所需的控制程序。圖3表示設定的初始條件，可以確定軟件在初始條件設置的step函數的正確性。通過Adams仿真分析得到絲桿螺母的前進速度（如圖4），從而可以間接通過公式計算出絲桿的轉速，計算公式為

式中：V為絲桿轉速；V1為絲桿螺母速度；d為絲桿導程。

得到絲桿的轉速，即可根據齒形帶的傳送比確定電動機的轉速，進而可以根據以上數據信息得到升降機構控制程序。

2.1.3 確定絲桿轉速

在上述的仿真中已經得到絲桿螺母的前進速度曲線，現定義絲桿的導程d為4 mm。得到絲桿的轉速曲線，如圖6所示。

圖6 絲桿轉速曲線

由圖6升降機構絲桿的轉速曲線，即可得到升降機構電動機的轉速，從而獲取控制程序所需的數據參數，完成升降機構的整體控制，計算公式為

式中：n為電動機轉速；n1為絲桿轉速；i為傳動比。

2.2 升降機構受力分析

2.2.1 添加驅動

運用Adams中motion調用外規劃數據SPLINE驅動，將已經仿真出的絲桿螺母運動速度變化曲線導入到Adams中作為螺母運動的驅動。

2.2.2 仿真分析

仿真獲得導軌耳座、固定耳座、兩者間角度α變化的曲線圖，如圖7～圖11所示。

根據圖7可以看出，升降機構的推桿在初期水平受力最大為460.85 N，隨著托板的上升推力逐漸減弱，最終達到95.64 N，這為絲桿螺母副和電動機的選型、推桿的安裝方式提供了依據。圖8和圖9表示的是導軌耳座和固定耳座在垂直方向所受的力，從圖中可以看出，在0～2.5 s期間，兩者受力趨于平穩，分別在300 N和40 N附近，到2.5 s開始出現突變，在3.7 s分別達到最大最小值，這為優化升降剪支機構提供了參考依據。圖10表示的是導軌耳座豎直方向的受力隨角度α變化的曲線，可以看出α=91°時受力最大為298.2547 N，在α=70°時受力最小為188.4809 N。圖11表示的是其水平方向所受的力與其角度變化，隨著時間的增加，水平受力在逐漸減小。圖10和圖11仿真結果符合實際工況，將每個α角度、導軌耳座受力情況表達出來，可以為導軌、滑塊和推桿的設計、選型和優化提供直觀的數據支持。

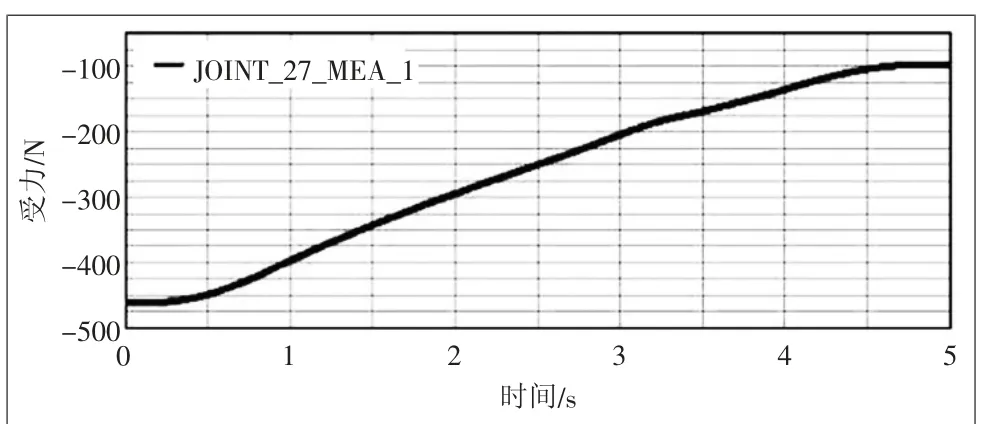
圖7 導軌耳座X軸受力變化曲線圖

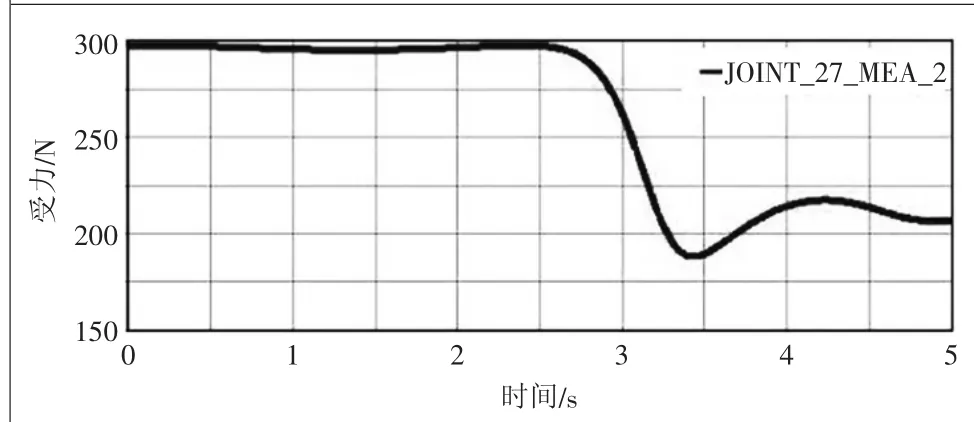
圖8 導軌耳座Y軸受力變化曲線圖

圖9 固定耳座Y軸受力變化曲線圖

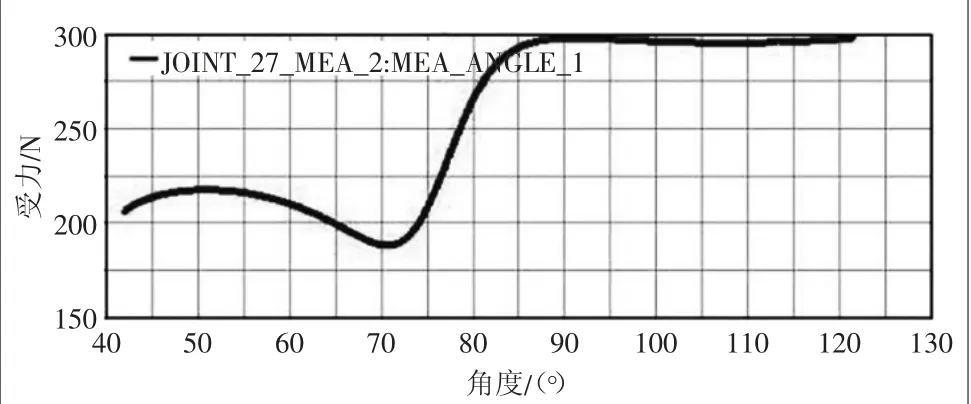
圖10 導軌耳座Y軸受力隨角度α變化曲線圖

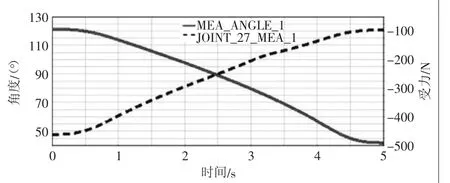
圖11 導軌耳座X軸受力與角度α隨時間變化曲線圖

3 升降機構驅動部件有限元仿真

3.1 材料屬性的定義與網格的劃分

將升降機構的驅動部件的三維模型導入到ANSYS Workbench軟件中，建立新材料軸承鋼GCr15，其材料參數為：彈性模量為219 GPa，泊松比為0.3，密度為7.81 g/cm3，屈服強度為518.42 MPa。

3.2 靜力學仿真

根據實際工況，在模擬部件添加相應的約束條件。根據前文2.2節中的受力分析得到推桿兩端水平受力為460.85 N，由受力平衡條件在螺母內孔壁施加一個反向作用力，力的大小為921.7 N。得到求解的云圖，如圖12～圖16所示。

圖12 總變形

圖13 等效應變

圖14 等效應力

圖15 最大主應力

圖16 最大剪切應力

根據圖12所示云圖，得出最大變形量為6.2659×10-2mm，發生在推桿的中心位置；最大等效應變為4.6543×10-4mm（如圖13），最大等效應力為38.551 MPa（如圖14），最大主應力為34.875 MPa（如圖15），最大剪切應力為20.892 MPa（如圖16），都發生在推桿兩端單獨一處螺紋孔處，其次應力大小的位置在導軌滑塊上表面與推桿的接觸位置周圍，對應力最大點進行強度計算，計算公式為

式中：[δ]為許用應力；δ1為極限應力值；n為安全系數。

因為導軌滑塊產生的摩擦力很小，可以忽略不計，為了避免其影響，更好地保證強度要求，現取安全系數為2。由于最大應力遠遠小于許用應力[δ]=δ1/2=259.21 MPa,所以模擬的機構滿足強度要求[5]。

通過對升降機構的力學仿真，可以通過仿真后的求解云圖很直觀地得到仿真部件的最大受力點和最大變形點，即危險點，并可以通過相關的數據參數計算判斷機構的強度特性，為機構初期的設計和后期的優化起到了關鍵作用。

4 結語

利用SolidWorks建模和ADAMS、ANSYS Workbench軟件對升降機構進行仿真分析，在保證升降拖板設計要求的同時，仿真計算出此升降機構設計與優化所需要的關鍵數據，模擬仿真結果與實際工況一致。通過仿真分析，得到每組剪支桿之間豎直方向的角度在42.07°～121.46°之間變化，絲桿螺母最大前進速度37.7043 mm/s，導軌耳座豎直方向最大受力為298.25 N, 水平最大受力460.85 N。推桿最大變形量為5.4001×10-2mm，最大應力為34.93 MPa，危險點發生在推桿兩端單獨一處螺紋孔處，其次是在導軌滑塊上表面與推桿的接觸位置邊緣周圍。整個仿真過程可作為絲桿螺母副和電動機的選型、升降機構導軌等機構的設計和優化提供參考與依據，同時可以為升降機構的疲勞強度分析提供數據支持。