基于 Nurbs 曲面引入 Kriging 近似模型對(duì)殼體結(jié)構(gòu)進(jìn)行拓?fù)鋬?yōu)化

談鳳婕

（華東建筑設(shè)計(jì)研究院有限公司，上海 200011）

0 引言

在空間曲面殼體結(jié)構(gòu)的設(shè)計(jì)中，合理的曲面可以提高結(jié)構(gòu)空間傳力性能。對(duì)于復(fù)雜的曲面結(jié)構(gòu)，普通的方程不能簡(jiǎn)單有效地表達(dá)曲面，可能需要多段曲線方程來(lái)擬合曲面殼體結(jié)構(gòu)，同時(shí)增加優(yōu)化變量的數(shù)量，增加優(yōu)化的計(jì)算量，降低優(yōu)化效率。利用 Nurbs 曲面，可以通過(guò)調(diào)整曲面上的控制點(diǎn)來(lái)改變曲面形狀，不僅可以靈活擬合曲面，而且可以控制優(yōu)化變量，提高優(yōu)化效率。

國(guó)內(nèi)外學(xué)者在利用 Nurbs 進(jìn)行建模分析的方面展開(kāi)了多項(xiàng)研究。文獻(xiàn)［1］利用 Nurbs 對(duì)球艏構(gòu)型進(jìn)行拓?fù)鋬?yōu)化；文獻(xiàn)［2］利用 Nurbs 對(duì)葉輪進(jìn)行建模分析；文獻(xiàn)［3］利用 Nurbs 對(duì)汽車殼體進(jìn)行模擬建模；文獻(xiàn)［4］基于 Nurbs提出 TOP-IGA-MMV 方法。

在結(jié)構(gòu)的拓?fù)鋬?yōu)化中，當(dāng)設(shè)計(jì)變量的個(gè)數(shù)變多時(shí)，往往需要更多的迭代步驟以找到全局最優(yōu)解，然而在結(jié)構(gòu)分析中，當(dāng)結(jié)構(gòu)形式復(fù)雜，單元?jiǎng)澐謹(jǐn)?shù)量大時(shí)，有限元分析本身就非常耗費(fèi)時(shí)間，再加上優(yōu)化分析的迭代數(shù)量，使得優(yōu)化過(guò)程計(jì)算效率十分低下。為了解決計(jì)算效率的問(wèn)題，引入 Kriging metamodel 來(lái)近似模擬真實(shí)模型，從而簡(jiǎn)化計(jì)算過(guò)程。

國(guó)內(nèi)外有大量對(duì)近似模型的研究和應(yīng)用。文獻(xiàn)［5-6］證明了 Kriging metamodel 可以提供一個(gè)很好的近似模型來(lái)模擬真實(shí)模型；文獻(xiàn)［7］對(duì)比了多種近似模型應(yīng)用于考慮不確定因素時(shí)的優(yōu)化問(wèn)題，發(fā)現(xiàn) Kriging metamodel的精度最好。

本文利用 Nu r b s 對(duì)殼體建模，生成網(wǎng)格，利用 Ansys 進(jìn)行有限元分析，通過(guò)調(diào)整控制點(diǎn)的位置改變殼體形狀，利用遺傳算法找尋控制點(diǎn)最優(yōu)位置，以殼體的應(yīng)變能最小作為目標(biāo)函數(shù)，引入近似模型簡(jiǎn)化優(yōu)化分析過(guò)程，尋找最優(yōu)化的殼體曲面形狀。

1 Nurbs 曲面

Nurbs 是 B-spline 通過(guò)等參轉(zhuǎn)換得到。B-spline 的基本方程有很多構(gòu)成方法，目前最常用的是由 Piegl 和Tiller 提出的 Cox-de Boor recursion 方程，假設(shè)｛ui｝（i=0，2，3，…，m）是一系列非減結(jié)點(diǎn)（ui≤ui+1）中的第 i 個(gè)結(jié)點(diǎn)，則在半開(kāi)區(qū)間［ui，ui+1）上的 p 階基本方程如式（1）所示。

式中：n，m，p 滿足 m=n+p+1。

然而 B-spline 不能靈活有效地表達(dá)一個(gè)圓，因此通過(guò)等參轉(zhuǎn)換，得到 Nurbs（見(jiàn)圖 1），則 p 階Nurbs 曲線表達(dá)式如式（3）所示。

式中：wi是和控制點(diǎn)Pi相關(guān)的權(quán)系數(shù)。將曲線擴(kuò)展到曲面，得到 Nurbs 曲面的表達(dá)式如式（4）所示。

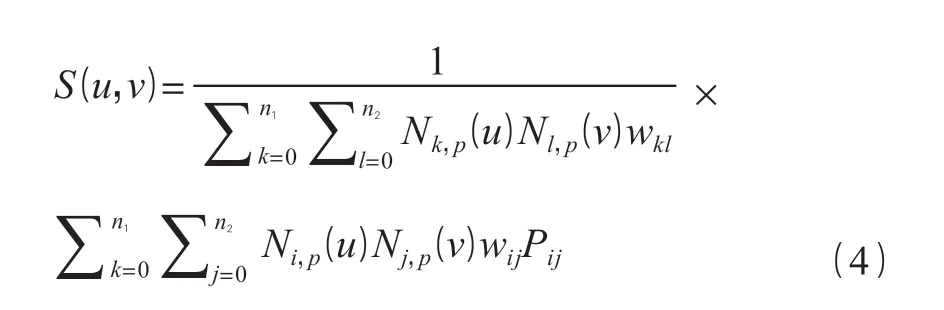
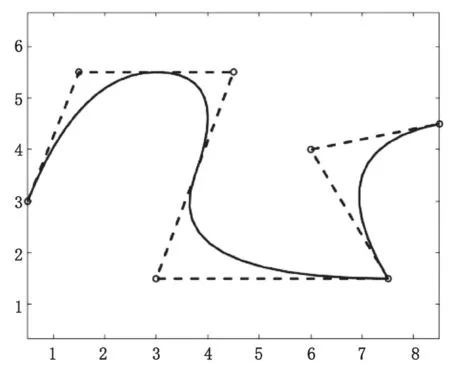
圖1 Nurbs 曲線

2 殼體結(jié)構(gòu)拓?fù)鋬?yōu)化實(shí)例

當(dāng)需要建立一個(gè)比較復(fù)雜的幾何形狀時(shí)，通過(guò)分析方程去建立該幾何形狀，會(huì)導(dǎo)致曲線分段過(guò)多，分析方程太復(fù)雜，計(jì)算不方便等問(wèn)題，然而通過(guò)移動(dòng)控制點(diǎn)來(lái)得到想要的幾何形狀是一種比較靈活有效的方式。

本文案例為一個(gè)蝴蝶形空間大跨殼體結(jié)構(gòu)，x 向跨度 280 m，y 向跨度 115 m，底部支撐由剪力墻和搖擺柱組成。本文只探討結(jié)構(gòu)形狀的優(yōu)化，只從結(jié)構(gòu)形狀建模的角度出發(fā)。選取殼上 12 個(gè)控制點(diǎn)建立結(jié)構(gòu)的幾何形狀，如圖 2 所示。

2.1 優(yōu)化方程

本文的目的是通過(guò)移動(dòng)建模時(shí)使用的 12 個(gè)控制點(diǎn)，來(lái)調(diào)整殼體各個(gè)位置的矢高，從而產(chǎn)生拱效應(yīng)，減小結(jié)構(gòu)產(chǎn)生的應(yīng)變能。因此選取 12 個(gè)控制點(diǎn)的豎向坐標(biāo)作為設(shè)計(jì)變量，控制點(diǎn)的豎向坐標(biāo)變化范圍為［2，20］，最小總應(yīng)變能為優(yōu)化目標(biāo)，則其相應(yīng)的優(yōu)化方程如式（5）所示。

圖2 初始模型

式中：x 是設(shè)計(jì)變量；f（x）是目標(biāo)方程；lb 是設(shè)計(jì)變量取值上邊界；ub 是設(shè)計(jì)變量取值下邊界。

2.2 優(yōu)化方法

本文使用的優(yōu)化算法是遺傳算法［8］，遺傳算法是一種全局優(yōu)化方法，其在指定的搜索區(qū)域內(nèi)，通過(guò)模仿遺傳學(xué)特性，將設(shè)計(jì)變量編碼后看作“染色體”，例如利用二進(jìn)制編碼，將染色體組合交叉和變異逐代演化出更好的近似解，從而得到全局最優(yōu)解。遺傳算法流程圖如圖 3 所示。

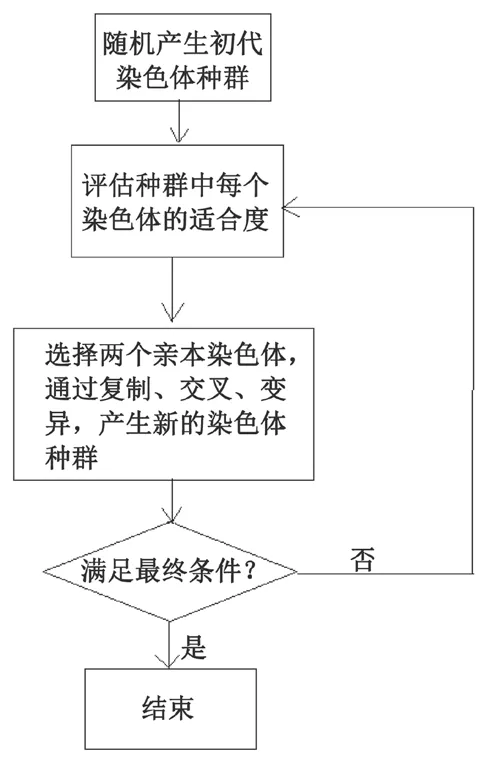
圖3 遺傳算法流程圖

利用遺傳算法對(duì)上述殼體進(jìn)行優(yōu)化，優(yōu)化后得到的結(jié)構(gòu)形狀如圖 4 所示，得到結(jié)構(gòu)的應(yīng)變能分布如圖 5 所示。

3 利用近似模型進(jìn)行優(yōu)化

圖4 優(yōu)化模型

圖5 應(yīng)變能分布（單位：kJ）

在結(jié)構(gòu)的拓?fù)鋬?yōu)化中，當(dāng)設(shè)計(jì)變量的個(gè)數(shù)變多時(shí)，往往需要更多的迭代步驟以找到全局最優(yōu)解，然而在結(jié)構(gòu)分析中，當(dāng)結(jié)構(gòu)形式復(fù)雜，單元?jiǎng)澐謹(jǐn)?shù)量大時(shí)，有限元分析本身就非常耗費(fèi)時(shí)間，再加上優(yōu)化分析的迭代數(shù)量，使得優(yōu)化過(guò)程計(jì)算效率十分低下，因此，需要引入新的方法來(lái)提高計(jì)算效率。考慮利用近似模型，建立設(shè)計(jì)變量和優(yōu)化目標(biāo)之間的關(guān)系，可以減小優(yōu)化分析時(shí)對(duì)結(jié)構(gòu)進(jìn)行有限元分析的次數(shù)，從而提高優(yōu)化效率，減少計(jì)算時(shí)間。

Kriging 是一種依據(jù)協(xié)方差函數(shù)［9］，根據(jù)已知數(shù)據(jù)建立一個(gè)空間模型來(lái)進(jìn)行預(yù)測(cè)的回歸算法。在特定的隨機(jī)過(guò)程中，Kriging 可以給出最佳的線性無(wú)偏估計(jì)。假設(shè)建模對(duì)象遵循高斯隨機(jī)過(guò)程，則得到相應(yīng)的 Kriging metamodel 如式（6）所示。

式中： βTf（x）是這個(gè)高斯隨機(jī)過(guò)程的平均值，βTf（x）=β1f1+β2f2+…+βPfP）；Z［x，R（x，x′；θ）］是一個(gè)均值為零的高斯隨機(jī)過(guò)程；σ2是該高斯隨機(jī)過(guò)程的方差；R（x，x′；θ）是觀測(cè)點(diǎn)與預(yù)測(cè)點(diǎn)之間的相關(guān)函數(shù)；θ是模擬空間的相關(guān)長(zhǎng)度。

Kriging metamodel 的計(jì)算原理為通過(guò)已知的設(shè)計(jì)點(diǎn) X={x1，x2，x3，…，xN}T和相應(yīng)的輸出值 y={y1，y2，y3，…，yN}T來(lái)預(yù)測(cè)在點(diǎn) x 處的Y＾=μk（x），根據(jù)式（6）可知，設(shè)計(jì)點(diǎn)和預(yù)測(cè)點(diǎn)服從高斯聯(lián)合分布，如式（7）所示。

式中：Fij=fj（xi）（j=1，2，…，P；i=1，2，…，N）；R 為已知值與預(yù)測(cè)值之間的相關(guān)函數(shù)（見(jiàn)圖 6）；θ 為相關(guān)長(zhǎng)度。常用的相關(guān)函數(shù)有線性相關(guān)函數(shù)、指數(shù)相關(guān)函數(shù)、高斯相關(guān)函數(shù)、Markov 相關(guān)函數(shù)。

圖6 相關(guān)函數(shù)（其中 θ=1，τ=x-x′=1）

利用 Kriging metamodel 建立模型的設(shè)計(jì)變量和目標(biāo)方程的近似模型，其中相關(guān)函數(shù)為指數(shù)相關(guān)函數(shù)。隨機(jī)生成 50 個(gè)樣本，得到真實(shí)模型和近似模型間的對(duì)比，如圖 7 所示。

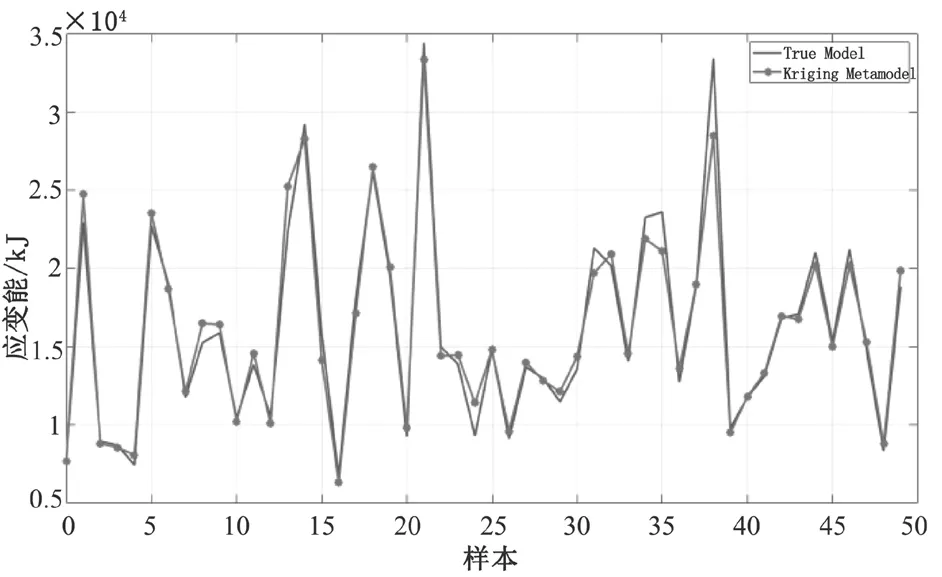
圖7 真實(shí)模型和近似模型之間的對(duì)比

利用近似模型來(lái)對(duì)設(shè)計(jì)變量進(jìn)行優(yōu)化，得到優(yōu)化模型如圖 8 所示，近似模型優(yōu)化結(jié)果和真實(shí)模型優(yōu)化結(jié)果對(duì)比如表 1 所示。

圖8 優(yōu)化模型

圖9 應(yīng)變能分布（單位：kJ）

表1 真實(shí)模型優(yōu)化結(jié)果和近似模型優(yōu)化結(jié)果對(duì)比

由表 1 可以看出，由近似模型計(jì)算通過(guò)有限元法所得到的優(yōu)化結(jié)構(gòu)的應(yīng)變能為 4.386×103kJ，由有限元法計(jì)算的通過(guò)真實(shí)模型得到的優(yōu)化結(jié)構(gòu)的應(yīng)變能為 4.066×103kJ，由近似模型計(jì)算通過(guò)近似模型得到的優(yōu)化結(jié)構(gòu)的應(yīng)變能為 3.956×103kJ，由有限元法計(jì)算通過(guò)近似模型得到的優(yōu)化結(jié)構(gòu)的應(yīng)變能為 4.386×103kJ。近似模型能夠預(yù)判設(shè)計(jì)變量和優(yōu)化目標(biāo)間的關(guān)系，由近似模型得到的優(yōu)化結(jié)果接近真實(shí)模型的優(yōu)化結(jié)果，然而由于近似模型存在誤差，使得由近似模型得到優(yōu)化結(jié)果并不是真實(shí)的最優(yōu)結(jié)果。

4 結(jié)論

本文利用 Nurbs 曲面建模，將控制點(diǎn)坐標(biāo)作為設(shè)計(jì)變量，通過(guò)調(diào)整控制點(diǎn)坐標(biāo)，利用遺傳算法優(yōu)化結(jié)構(gòu)形狀，避免了通過(guò)分析方程去建立幾何形狀時(shí)遇到的曲線分段過(guò)多、分析方程太復(fù)雜、計(jì)算不方便等問(wèn)題。

近似模型的應(yīng)用可以大幅地減少計(jì)算時(shí)間，簡(jiǎn)化分析過(guò)程，提高優(yōu)化效率。近似模型和真實(shí)模型的計(jì)算結(jié)果對(duì)比，近似模型能夠很好地預(yù)測(cè)設(shè)計(jì)變量和優(yōu)化目標(biāo)的關(guān)系。但是，近似模型和真實(shí)值之間仍然存在比較明顯的誤差，這會(huì)導(dǎo)致所得到結(jié)果接近最優(yōu)解，但不是最優(yōu)解。

整體來(lái)看，近似模型在結(jié)構(gòu)優(yōu)化中的應(yīng)用是一種非常有前景的方法，但是仍需要通過(guò)引入一些措施，比如神經(jīng)網(wǎng)絡(luò)算法、貝葉斯定理等，來(lái)提高近似模型的精確度，減小誤差，使得近似模型可以更好地模擬真實(shí)結(jié)構(gòu)模型。Q