基于Harary圖生成樹的部分重復碼構造①

張鑫楠,沈克勤,孫 偉,何亞錦

(長安大學 信息工程學院,西安 710061)

目前,將海量數據存儲在分布式存儲系統中的不同存儲節點上的數據存儲方式已在實際系統中得到了廣泛應用,如Google 文件系統[1]、Hadoop 文件系統等.為確保分布式存儲系統中數據的可用性和可靠性,通常采用諸如復制策略[2]或糾刪碼策略[3,4]的數據冗余策略.以復制策略中的三副本復制為例,三副本復制需要存儲大量副本數據以確保系統較高的可靠性,存儲代價過高;糾刪碼策略的提出使得修復造成的存儲開銷顯著降低,但其過大的修復帶寬開銷也成為了限制它的瓶頸.

2007年,Dimakis 等人指出存儲開銷和修復帶寬開銷之間存在某種平衡,平衡曲線上的點可通過再生碼來實現[5].再生碼基于網絡編碼的概念,其故障節點可通過連接一定數目的存活節點完成修復,相比于糾刪碼降低了修復帶寬開銷.目前再生碼的研究主要集中在最小存儲再生碼和最小帶寬再生碼[6].

El Rouayheb和Ramchandran為進一步降低修復過程中的運算復雜和帶寬開銷,提出了一種基于最小帶寬再生點的精確修復編碼-部分重復(Fractional Repetition,FR)碼[7].部分重復碼結合再生碼和復制策略的優點,有效減少了修復帶寬開銷和磁盤I/O 開銷[8],并實現精確的無編碼修復.

目前,FR 碼主要采用分組設計[9]、可分解設計[10,11]等方法進行構造.朱兵等人基于分組設計提出一種重復度異構的FR 碼的構造[12],使得常用數據的備份更加充分,且參數選取范圍較大,但同時也造成了較大的存儲開銷;Natalia Silberstein和Tuvi Etzion 等人基于組合設計和正則圖,提出了一種達到最大碼率的FR 碼的構造方法[13],但其重復度受FR 碼結構的約束,不能適用于任意參數;Harout Aydinian和Holger Boche 等人則基于部分有序集構造了一種普遍好的FR 碼[14],這種構造方法雖然簡便,但其重復度卻也十分受限.為此,本文基于Harary 圖生成樹構造出了一種新型的部分重復(Fractional Repetition based on Spanning trees of Harary graph,FRSH)碼,可以在很大范圍內選擇構造參數和數據塊的重復度,還能修復多個故障節點.通過調整Harary 圖的構造參數,可以構造出不同重復度的FR 碼.相比現有的FR 碼,采用Harary 圖生成樹設計FR 碼更加簡潔直觀.相較于RS 碼和SRC[15],FRSH 碼在修復帶寬開銷、修復復雜度以及修復局部性等方面得到了更低的開銷,且改善了修復效率,并將故障節點修復時間縮短.

1 預備知識

1.1 Harary 圖的基礎知識

Harary 圖是一種正則圖,定義為Hk,m,其中k為每個節點所鄰接的節點個數,即頂點的度;m為頂點個數.根據k和m的取值,可分為3 種情況構造Harary 圖.

(1)k是偶數

設k=2r,則H2r,m構造如下:先給出它的頂點0,1,2,…,i,…,j,…,m?1,然后連接所有滿足|i?j|≤r的頂點,即可完成H2r,m的構造.

(2)k是奇數,m是偶數

設k=2r+1,則H2r+1,m構 造如下:首先構造出H2r,m,為滿足k=2r+1,還需添加一些邊:這些邊連接了每個頂點i與頂點連接完即可得到H2r+1,m.

(3)k是奇數,m是奇數

設k=2r+1,此時的H2r+1,m構造如下:首先構造出H2r,m,為滿足k=2r+1,需要添加一些邊:這些邊連接了頂點0與頂點和再將每個頂點i連到頂點如此連接即可完成構造.

圖1所示是構造的k=4,m=8的Harary 圖H4,8.

1.2 生成樹的基礎知識

無圈圖是指不包含圈的圖,連通的無圈圖定義為樹.無圈圖的生成樹是指頂點與無圈圖相同、邊集是無圈圖的邊集子集,且含邊數最少的連通子圖.圖2中T1是完全圖K8的生成樹,它包含K8中的所有9個頂點,邊集是完全圖K8 邊集的子集,且包含了最小數目的邊數.

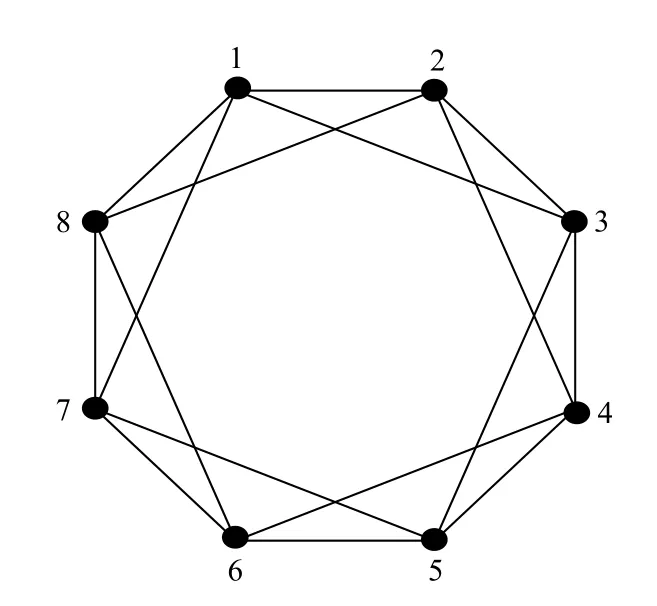
圖1 Harary 圖H4,8

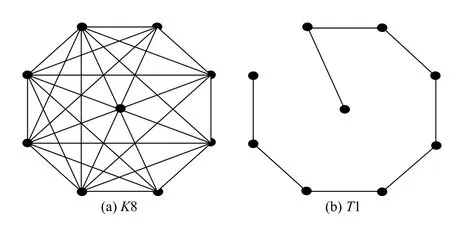
圖2 完全圖K8和它的生成樹T1

由構造的Harary 圖G=Hk,m,以頂點1為起始頂點得出生成樹.具體構造步驟如下[16]:

步驟1.畫出邊(1,v+1)和(1,m-v+1),v=1,2,…,

步驟2.令p=+1,j=,畫出邊(m?p+1,m?p?j+1),(m?p?j+1,m?p?2j+1),…,直到形成從頂點m?p+1 到頂點1的路徑時停止.

步驟3.令q=p+1,重復步驟2 畫出邊(m?q+1,m?q?j+1),(m?q?j+1,m?q?2j+1),…,當存在從頂點m?p+1 到頂點1的路徑時停止,否則轉至步驟1.

圖3為基于H4,8,且以頂點1為起始頂點構造的生成樹.

1.3 離心率的基礎知識

對于連通圖G的一個頂點v,v的離心率定義為v 到G中除v 外所有頂點的距離的最大值.例如圖4中頂點1的離心率值為3,由于距離頂點1 最長的頂點是頂點6,而從頂點1 到頂點6的路徑中共經過3個頂點,即距離為3,故頂點1的離心率,其它頂點同理.G的半徑定義為G中所有頂點離心率的最小值,直徑則定義為G的最大離心率,分別記為rad(G)和diam(G).在圖4中頂點最小離心率為2,最大離心率為4,所以有rad(G)=2,diam(G)=4.

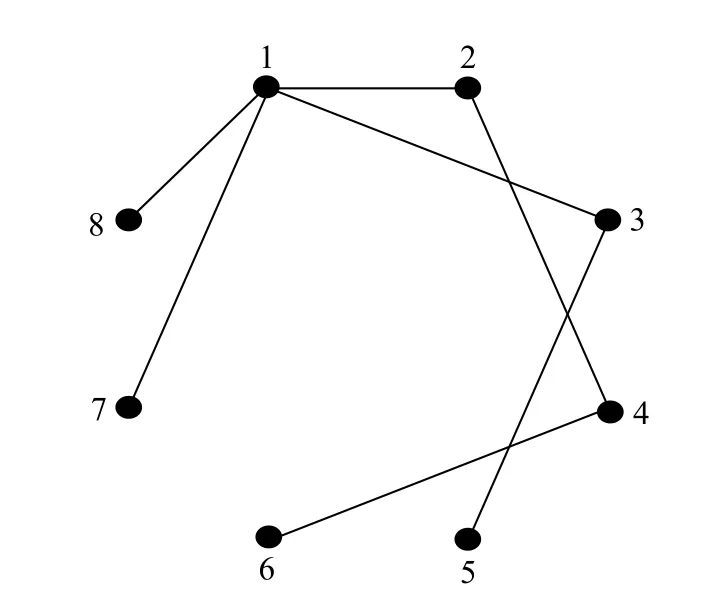
圖3 基于H4,8的生成樹

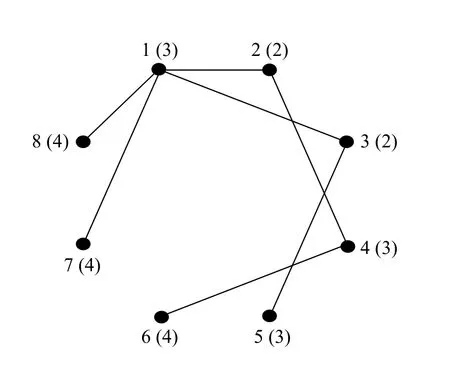
圖4 離心率參考圖

2 基于Harary 圖生成樹的部分重復碼構造

2.1 構造方法

ρ的FRSH 碼的構造算法,具體步驟如算法1.

基于Harary 圖生成樹與離心率,給出重復度為

算法1.基于Harary 圖生成樹的部分重復碼構造1)給定一個Harary 圖的設計參數k和m,其中k為每個節點所連接的節點個數,即節點的度,m為頂點個數,m>0.本文暫且只考慮k為偶數的情況.2)根據給出的設計參數k和m 構造Harary 圖.3)選定Harary 圖上任一頂點作為頂點1,并從頂點1 開始給Harary圖的頂點順時針編號,每個頂點存儲與其編號相同的數據塊.4)由構造的Harary 圖以頂點1為起始頂點構造生成樹.n(n≥1)5)對得到的生成樹的頂點按離心率分組,將第一個生成樹G的頂點按離心率分為組,分組后每組頂點的離心率相同,并將各組頂點按編號從小到大的順序分別寫入n個節點中,得到第一組節點.ρ(ρ≥1)ρ?1 n?(ρ?1)6)按照所需構造部分重復碼的重復度 更換起始頂點,重復步驟4)和步驟5)再得到個生成樹,并將它們的頂點按離心率分組后分別寫入個新的節點中.

M=(ms,t)1≤s≤nρ,1≤t≤m 7)由生成樹頂點按離心率的分組得到關聯矩陣 ().關聯矩陣構造公式如下(vt 代表生成樹中的任一頂點,es 代表任一離心率取值):ms,t=■■■■■■■■■1,若vt與es相關聯0,其它情況d ρ ρ再將生成樹的關聯矩陣等價為FR 碼的關聯矩陣,關聯矩陣的行向量對應FR 碼的存儲節點,列向量對應FR 碼的編碼塊.行向量的重表示表示節點存儲容量,列向量的重表示編碼塊重復度.由此即可得到重復度為的FR 碼.

綜上,重復度為ρ的FRSH 碼的構造過程中,其包含的不同數據塊個數即為Harary 圖的頂點數m;重復度 ρ由生成樹個數決定;包含的節點個數為nρ.

具體地,我們以構造 ρ=3的FR 碼的過程為例說明構造方法.令k=4,m=11,構造Harary 圖H4,11,并給其頂點編號,如圖5(a)所示.再由構造的Harary 圖以頂點1為起始頂點得出第一個生成樹,如圖5(b)所示.

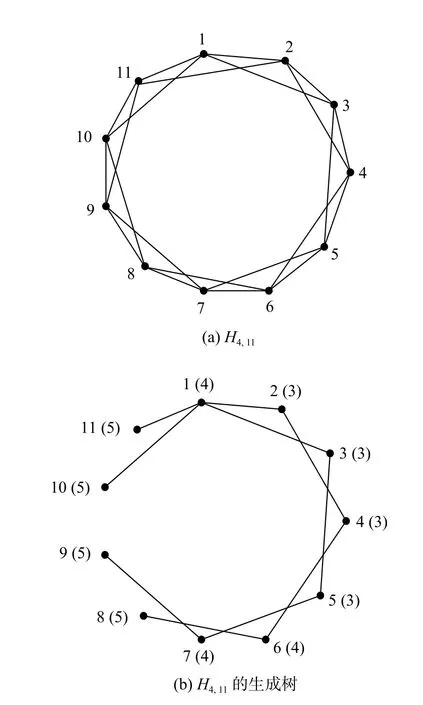
圖5 H 4,11和它的生成樹

將圖5(b)中給出的生成樹的頂點按離心率分組,相同離心率頂點對應的數據塊寫入同一分組.為滿足重復度 ρ=3,需重復步驟4)和步驟5),分別以頂點3和頂點5為起始頂點再得到第2個生成樹和第3個生成樹(此處圖略).進一步將第2個生成樹和第3個生成樹的頂點存儲數據按離心率分組,構造關聯矩陣M.以圖5(b)中的生成樹為例,本例中所有生成樹頂點的離心率es共有n=3個取值:e1=3、e2=4、e3=5.圖5(b)中頂點2、3、4、5的離心率都為e1=3,即v2、v3、v4、v5與e1相關聯,故有m1,2=m1,3=m1,4=m1,5=1,以此類推便得到關聯矩陣M.

根據關聯矩陣M,構造重復度 ρ=3的FR 碼,構成的FR 碼如圖6.

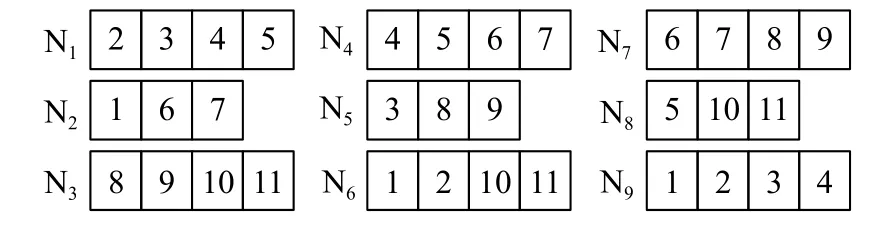
圖6 FR 碼

2.2 故障節點修復

本論文構造的任意FRSH 碼都包含 ρ個平行類,且最多可容忍 ρ?1個節點故障,具體修復方案如下:

(1)當單個節點失效時,新生節點從存活平行類中下載失效節點對應數據塊,即可完成修復.如節點N1故障時,損壞的數據塊2、3、4、5 可從剩余兩個平行類N4、N5、N6或N7、N8、N9中下載.這里選擇連接存活節點N4、N9并分別下載4、5、2、3,即可修復故障節點N1.

(2)當多個節點同時出現故障,由于仍至少存在一個平行類包含全部數據塊,而本方法構造的FR 碼的任一平行類中包含的節點個數等于離心率分組數n,故至多連接n個節點即可完成修復.具體地,當多個故障節點所包含的數據塊個數d<αmin+αmax(這里αmin和αmax分別表示FRSH 碼中節點存儲的最小數據塊個數和最大數據塊個數)時,僅需連接n?1個故障節點即可完成修復.例如當N2和N5同時失效時,故障節點N2和N5共包含d=6個數據塊,滿足d<αmin+αmax.此時,修復故障節點N2和N5需要連接n?1=2個存活節點完成修復.這里選擇存活節點N7和N9,并分別從存活節點N7和N9下載數據塊6、7、8、9和1、3,實現故障節點N2和N5的修復.

(3)當多個節點同時出現故障,且多個故障節點所包含的數據塊個數d≥αmin+αmax時,需連接n?1或n個不同節點即可完成故障節點修復.同樣先考慮圖6中的節點N4和N5發生故障,此時故障節點N4和N5包含d=7個數據塊,滿足d≥αmin+αmax.為修復故障節點N4和N5需要從n?1=2個存活節點中下載對應數據塊,這里選擇存活節點N1和N7,并分別從N1和N7下載數據塊3、4、5和6、7、8、9,即可修復故障節點N4和N5.另當N2和N7發生故障時,此時故障節點N2和N7包含d=7個數據塊,同樣滿足d≥αmin+αmax.而此時修復N2和N7需連接n=3個存活節點N4、N5和N6,并分別下載6、7、8、9和1 便可修復N2和N7.

綜上,對于重復度為ρ的FRSH 碼,修復單節點故障時在剩余平行類中連接對應存活節點(連接的節點數至多為n?1個)下載所需數據塊即可;修復多節點故障時,當多個故障節點所包含的數據塊個數d<αmin+αmax時,僅需連接n?1個故障節點即可完成修復;當多個故障節點所包含的數據塊個數d≥αmin+αmax時,需連接n?1或n個不同節點即可完成故障節點修復.

3 性能分析

基于Harary 圖生成樹構造的FR 碼的性能分析主要集中在修復局部性、修復帶寬開銷和運算復雜度這幾方面,并將其與傳統的RS 碼和簡單再生碼(Simple Regenerating Codes,SRC)進行性能比較.表1給出了SRC、RS 碼與FRSH 碼在一般情況下的的節點存儲開銷、修復帶寬開銷以及修復局部性的計算公式,之后我們會在給定具體文件大小和編碼數據等條件下用柱狀圖的形式把上文構造的ρ=3的FR 碼與SRC、RS 碼的各種性能逐一進行比較.

表1 幾種編碼方案的性能分析

3.1 修復局部性

修復局部性是衡量構造出的部分重復碼性能的重要指標之一,其定義為節點故障修復過程中連接的存活節點數目,即磁盤I/O 開銷.此處為方便比較,我們假設原文件大小M=1000 Mb,存儲節點數則為n=11,SRC 子文件數f=3,RS 碼和SRC的原文件重構度為k=8,FRSH 碼外部采用(11,8)MDS 編碼.本小節僅考慮兩種節點故障情況:單節點故障與兩節點故障.

當單節點出現故障時,SRC在修復失效節點時需要連接2f個節點,這里取f=3,則SRC的修復局部性為6;若采用(11,8)RS 碼,需要連接k=8個節點以恢復出完整的原文件,再由原文件修復故障節點,故其修復局部性為8;而本文構造的FRSH 碼需要連接2個節點來修復故障節點,修復局部性為2.

在兩節點故障的情況下,SRC與(11,8)RS 碼都需要連接k=8個存活節點以修復故障節點,故它們的修復局部性都為8;而基于Harary 圖生成樹構造的FRSH碼的修復局部性為2 或3,為便于對比,此處取恒為3 作為比較.由圖7可見,在單節點故障與兩節點故障情況下,本文構造的FRSH 碼的修復局部性都優于SRC和RS 碼.

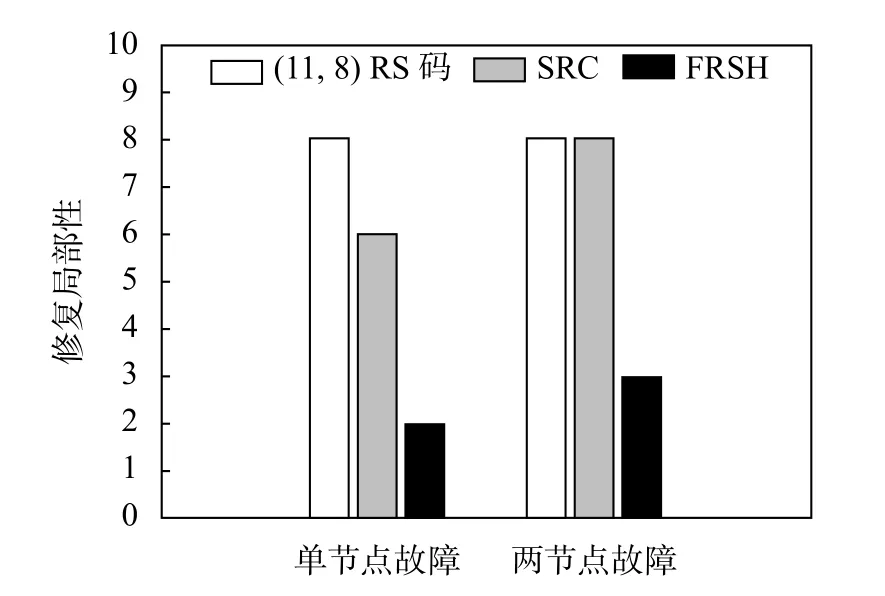
圖7 修復局部性

另與基于圖因子構造的部分重復碼相比,在單節點故障時兩種部分重復碼都需要連接兩個節點進行修復;在兩節點故障時,基于圖因子的部分重復碼需要連接4個節點進行修復,而FRSH 碼至多需連接3個節點進行修復,可見在兩節點故障時FRSH 碼具有顯著優勢.

3.2 修復帶寬開銷

在單節點故障的情況下,SRC 需下載f個數據塊以完成修復,而每個數據塊的大小為M/fk,因此SRC的帶寬開銷為(f+1)M/k;由于RS 碼在單節點故障的情況下完成修復需下載整個原文件,故RS 碼的帶寬開銷為原文件大小M;而本文構造的FRSH 碼在單節點故障的情況下需要通過連接2個存活節點完成修復,因此FRSH 碼的帶寬開銷為2M/k.

當兩節點同時故障時,RS 碼與SRC的帶寬開銷均為M.FRSH 碼的帶寬開銷為3M/k.

假設原文件大小為M=1000 Mb,存儲節點數n=11,SRC 子文件數f=3,RS 碼和SRC的原文件重構度為k=8,FRSH 碼外部采用(11,8)MDS 編碼.當單節點故障時,RS 碼的帶寬開銷為1000 Mb,SRC的帶寬開銷為500 Mb,FRSH 碼的帶寬開銷為250 Mb;當兩個節點故障時,(11,8)RS 碼修復帶寬開銷為1000 Mb,SRC的帶寬開銷同樣為1000 Mb,為方便對比FRSH 碼的帶寬開銷取較大值3M/k=375 Mb.如圖8所示,無論單節點還是兩節點故障,FRSH 碼的修復帶寬開銷都相對較低.

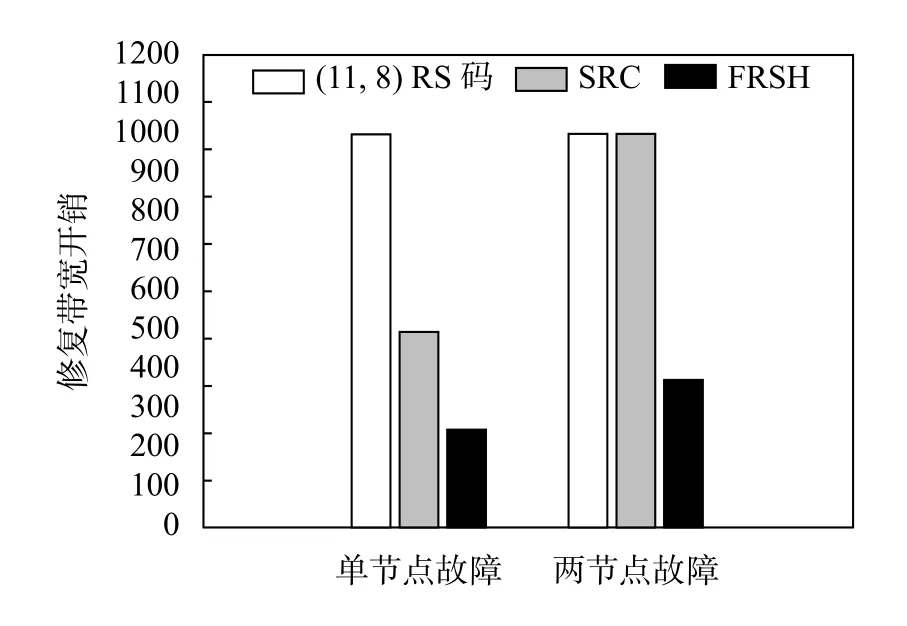
圖8 修復帶寬開銷對比

3.3 構造算法運算復雜度

除去修復局部性與修復帶寬開銷這兩種直觀性能,構造算法復雜度體現了算法在執行時的難易程度,是衡量一個算法好壞的重要指標.所謂運算復雜度,即將算法寫成程序在實際的計算機系統中運行時涉及的計算量.本文構造的FRSH 碼構造時不需要任何計算量,只需調節Harary 圖與其生成樹的參數即可.相較于可達到同等性能的FRC,減少了大量的運算時間.

將基于Harary 圖生成樹的FRSH與運用圖因子分解構造的FRC[17]在構造算法運算復雜度進行對比分析,在文獻[17]中,構造算法時運用到了加法,乘法運算和基于一次方程上的運算共3 種運算方式,相較于本文僅需調整Harary 圖參數,可知本文的構造算法運算復雜度更優.

4 結論與展望

針對部分重復碼的有效修復問題,本文基于Harary圖生成樹構造出了一種新型的部分重復碼.這種FRSH碼在構造方面的優勢在于參數選擇范圍較廣且運算復雜度極低.在性能方面,實驗結果表明,相較于現有的RS 碼和SRC,FRSH 碼在修復帶寬開銷、修復局部性等方面得到了更低的開銷,且改善了修復效率,并將故障節點的修復時間縮短;又與可達到類似性能的圖因子分解的部分重復碼在運算復雜度方面進行比較,得出本文的構造算法運算復雜度更優.