改進(jìn)Apriori 算法在學(xué)生能力影響因子分析中的應(yīng)用

劉 磊，康瑞華

（湖北工業(yè)大學(xué)計(jì)算機(jī)學(xué)院，湖北武漢 430072）

0 引言

隨著信息技術(shù)的發(fā)展與智能時(shí)代的到來，社會(huì)教育系統(tǒng)的變革逐漸頻繁，學(xué)生綜合素質(zhì)能力培養(yǎng)顯得尤為重要。本文通過對(duì)2 000 多名來自不同地域、不同學(xué)校與不同專業(yè)的大一、大二學(xué)生的問卷調(diào)查，應(yīng)用Apriori 算法分析其學(xué)習(xí)生涯中曾進(jìn)行的能力培養(yǎng)對(duì)當(dāng)前大學(xué)時(shí)期綜合素質(zhì)的影響，從而給予當(dāng)前學(xué)生成長(zhǎng)過程中多元化教育選擇以方向性指導(dǎo)［1］。

1 相關(guān)研究

大數(shù)據(jù)是繼云計(jì)算、物聯(lián)網(wǎng)之后，計(jì)算機(jī)行業(yè)又一次顛覆性的技術(shù)革命。大數(shù)據(jù)挖掘與應(yīng)用可創(chuàng)造出很高的經(jīng)濟(jì)價(jià)值，將是未來計(jì)算機(jī)領(lǐng)域最大的市場(chǎng)機(jī)遇之一［2］。大數(shù)據(jù)的應(yīng)用在生活中也屢見不鮮，例如大數(shù)據(jù)在電視臺(tái)數(shù)據(jù)處理中的應(yīng)用［3］、大數(shù)據(jù)在金融投資中的應(yīng)用［4］、關(guān)聯(lián)分析在教育領(lǐng)域的應(yīng)用等［5-17］。

在大數(shù)據(jù)應(yīng)用過程中，其常常引發(fā)人們對(duì)算法本身的思考。我國(guó)近年來在大數(shù)據(jù)分析領(lǐng)域的研究進(jìn)展很快，在研究起始階段，劉君強(qiáng)等［18］收集整理近年來關(guān)于關(guān)聯(lián)規(guī)則的詳細(xì)研究，針對(duì)大數(shù)據(jù)分析領(lǐng)域的新進(jìn)展進(jìn)行綜述與分析，并根據(jù)基礎(chǔ)大數(shù)據(jù)分析算法Apriori 的特點(diǎn)，提出Apriori 算法優(yōu)化的初步方向與思想。之后，王偉勤等［19］提出改進(jìn)Apriori 算法的具體內(nèi)容，即采用基于數(shù)組，且避免Apriori 的匹配模式，通過只掃描一次，同時(shí)減少算法內(nèi)存占用空間的方式提高算法效率，并對(duì)該方法進(jìn)行驗(yàn)證，但其仍存在兩個(gè)關(guān)鍵問題：掃描次數(shù)與剪枝效率。本文在此基礎(chǔ)上對(duì)掃描方式和數(shù)據(jù)結(jié)構(gòu)存儲(chǔ)兩個(gè)關(guān)鍵問題進(jìn)行優(yōu)化與改進(jìn)，通過分析學(xué)生能力影響因子，探究Apriori 算法的改進(jìn)思路與方法。

2 Apriori 算法

Apriori 算法常用的頻繁項(xiàng)集評(píng)估標(biāo)準(zhǔn)有3 個(gè)：支持度、置信度和提升度。其中，支持度是關(guān)聯(lián)數(shù)據(jù)在數(shù)據(jù)集中出現(xiàn)的概率，支持度高的數(shù)據(jù)不一定構(gòu)成頻繁項(xiàng)集，但是構(gòu)成頻繁項(xiàng)集的數(shù)據(jù)支持度肯定不低。置信度則體現(xiàn)一個(gè)數(shù)據(jù)出現(xiàn)后，另一個(gè)數(shù)據(jù)出現(xiàn)的概率，即數(shù)據(jù)的條件概率。如大學(xué)生幼年培訓(xùn)奧數(shù)對(duì)應(yīng)鋼琴的置信度為60%，支持度為5%，說明總共有5%的學(xué)生在幼年培訓(xùn)了奧數(shù)和鋼琴，培訓(xùn)了奧數(shù)的學(xué)生中有60%的人培訓(xùn)了鋼琴。提升度則表示兩個(gè)數(shù)據(jù)之間的管理關(guān)系，也即在培訓(xùn)奧數(shù)的情況下同時(shí)培訓(xùn)鋼琴的概率與培訓(xùn)鋼琴總體發(fā)生概率之比。若提升度大于1，則鋼琴?奧數(shù)是有效的強(qiáng)關(guān)聯(lián)規(guī)則；若提升度小于等于1，則鋼琴?奧數(shù)是無效的強(qiáng)關(guān)聯(lián)規(guī)則［8，14-16］。

Apriori 算法采用逐層搜素策略，同時(shí)依據(jù)其性質(zhì)壓縮搜索空間。其基本思想在于，首先掃描一次事務(wù)數(shù)據(jù)集，找出頻繁一項(xiàng)集集合L1，然后基于L1產(chǎn)生所有可能的頻繁二項(xiàng)集即候選集C2，篩選出候選項(xiàng)集C2中所有滿足最小置信度的項(xiàng)集，組成頻繁項(xiàng)集L2。用上述步驟重復(fù)處理新得到的頻繁項(xiàng)集Lx，直至再也找不出頻繁項(xiàng)集時(shí)退出［17-19］。

在Apriori 算法中，候選項(xiàng)集的生成可分成連接和剪枝兩部分。為提高剪枝效率，運(yùn)用了以下兩個(gè)重要定律：

定律1 如果k維數(shù)據(jù)項(xiàng)Xk是頻繁項(xiàng)集，則其k-1 維子集都是頻繁項(xiàng)集。

定律2 如果k-1 維數(shù)據(jù)項(xiàng)Xk-1不是頻繁項(xiàng)集，則其k維超集都不是頻繁項(xiàng)集。

2.1 Apriori 算法改進(jìn)思想

Apriori 算法得到了廣泛運(yùn)用，主要由于其算法結(jié)構(gòu)簡(jiǎn)單易懂、便于理解，沒有復(fù)雜的公式推導(dǎo)［2］。通過運(yùn)用兩個(gè)重要定律，使得算法候選集的規(guī)模大幅減小，相應(yīng)算法運(yùn)算速度大幅提高，但其仍存在兩個(gè)影響內(nèi)存及效率的問題：①事務(wù)數(shù)據(jù)庫(kù)掃描次數(shù)過多。每次尋找頻繁項(xiàng)集都需要掃描一次事務(wù)數(shù)據(jù)庫(kù)，最終尋找到長(zhǎng)度為k的頻繁項(xiàng)集共需掃描k次，所以當(dāng)數(shù)據(jù)庫(kù)或k很大時(shí)，算法耗時(shí)將呈幾何式增長(zhǎng)；②在執(zhí)行候選集的剪枝操作時(shí)，對(duì)數(shù)據(jù)庫(kù)的掃描次數(shù)過多。而且當(dāng)候選集與自身連接時(shí)也要對(duì)數(shù)據(jù)庫(kù)進(jìn)行多次掃描，導(dǎo)致算法在廣度優(yōu)先方面的適應(yīng)性很差［10-13］。

本文將從兩方面對(duì)現(xiàn)有Apriori 算法進(jìn)行改進(jìn)：

（1）針對(duì)事務(wù)數(shù)據(jù)庫(kù)掃描次數(shù)過多的問題，本文主要借鑒了文獻(xiàn)［4］的思想，采用與傳統(tǒng)Apriori 算法不同的數(shù)據(jù)結(jié)構(gòu)，將水平的事務(wù)數(shù)據(jù)庫(kù)（見表1）轉(zhuǎn)變?yōu)榇怪钡臄?shù)據(jù)結(jié)構(gòu)（見表2）。

Table 1 Transaction database表1 事務(wù)數(shù)據(jù)庫(kù)

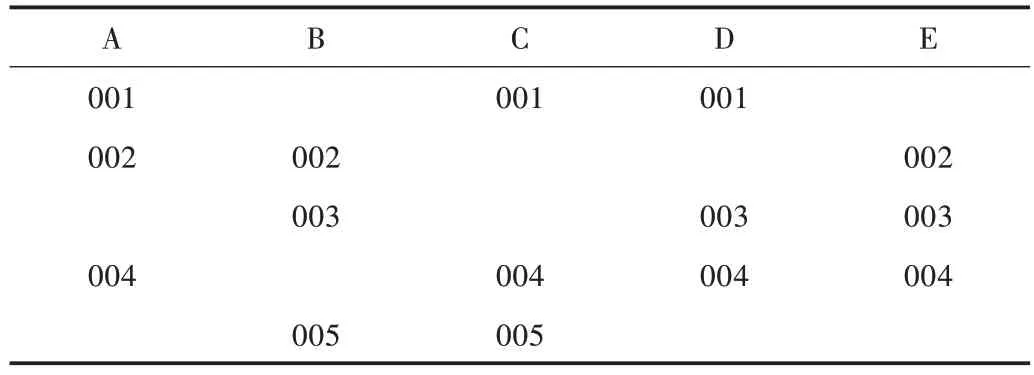
Table 2 Project database表2 項(xiàng)目數(shù)據(jù)庫(kù)

通過這種轉(zhuǎn)換將事務(wù)數(shù)據(jù)庫(kù)垂直化，只需掃描一次數(shù)據(jù)庫(kù)即可完成數(shù)據(jù)分析，并且更容易得到支持k維數(shù)據(jù)項(xiàng)的事務(wù)數(shù)。

（2）針對(duì)冗余數(shù)據(jù)項(xiàng)過多、剪枝次數(shù)過多以及連接產(chǎn)生數(shù)據(jù)項(xiàng)空間較大的問題，本文利用算法的兩個(gè)定律推斷出第3 個(gè)定律：

定律3 對(duì)于k維數(shù)據(jù)項(xiàng)x={i1,i2,i3…,ik}，如果存在一個(gè)元素j?x，使表示在k-1維頻繁項(xiàng)集中包含j的數(shù)量)，則x不是頻繁項(xiàng)集。

證明：若x是k維頻繁項(xiàng)集，則由定律1 可得，其共有=k個(gè)k-1 維子集為頻繁項(xiàng)集，其中包含j的共有=k-1 個(gè)。由于上述子集均為頻繁項(xiàng)集，故得到≥k-1，與假設(shè)矛盾，所以x不是k維頻繁項(xiàng)集。

從這一定律可以得出：如果在Lk-1中有一元素j，且有＜k-1，則所有包含元素j的k-1 維頻繁項(xiàng)集不參與連接。

2.2 改進(jìn)后的Apriori 算法描述

相關(guān)定義如下：

3 數(shù)據(jù)分析

本文通過分析當(dāng)前中小學(xué)教育政策、大學(xué)生培養(yǎng)計(jì)劃、企業(yè)需求以及大學(xué)新生心理，設(shè)計(jì)了關(guān)于大學(xué)生能力培養(yǎng)方式與當(dāng)前時(shí)期適應(yīng)力、自信心的調(diào)查問卷，并通過問卷星發(fā)放到包括985、211、普通高校在內(nèi)的10 所高校，回收問卷共計(jì)2 812 份。之后使用Apriori 算法進(jìn)行數(shù)據(jù)分析，Apriori 算法是一種挖掘布爾關(guān)聯(lián)規(guī)則頻繁項(xiàng)集（Bourg association rules frequent itemsets）的經(jīng)典算法，用來尋找數(shù)據(jù)值中頻繁出現(xiàn)的數(shù)據(jù)集合。本文通過尋找當(dāng)前大學(xué)生曾經(jīng)參與過的多元化培訓(xùn)對(duì)其綜合素質(zhì)與自信心影響最大的特征數(shù)據(jù)結(jié)果集，根據(jù)該結(jié)果集為當(dāng)前教育過程中的多元化能力個(gè)性培訓(xùn)提供指導(dǎo)性方案。

根據(jù)大學(xué)生當(dāng)前的綜合素質(zhì)情況對(duì)2 812 份調(diào)查問卷進(jìn)行分類，并設(shè)計(jì)特征因子與權(quán)值，運(yùn)用本文改進(jìn)的Apriori算法進(jìn)行分析。

3.1 垂直數(shù)據(jù)庫(kù)建立

將收集的數(shù)據(jù)按照表2 的數(shù)據(jù)結(jié)構(gòu)錄入項(xiàng)目數(shù)據(jù)庫(kù)，調(diào)查結(jié)果中的每一項(xiàng)包含多個(gè)選項(xiàng)，如果每個(gè)選項(xiàng)都由一個(gè)數(shù)據(jù)進(jìn)行記錄，則需要龐大的數(shù)據(jù)空間進(jìn)行記錄（若有4個(gè)選項(xiàng)則需4 位，但采用下述方法只需2 位）。在實(shí)際數(shù)據(jù)分析過程中，為每個(gè)選項(xiàng)進(jìn)行編碼，如針對(duì)“結(jié)業(yè)成果是否有用”這一項(xiàng)，可進(jìn)行如下二進(jìn)制編碼：00：有很大作用；01：有作用但不大；10：基本沒什么作用。該方法相比位存儲(chǔ)有效減少了數(shù)據(jù)存儲(chǔ)空間。為更直觀地理解算法過程，下述分析示例不按以上方法進(jìn)行編碼處理，而是直接用數(shù)據(jù)名稱表示，如表3 所示。

Table 3 Diversity capability database表3 多元化能力數(shù)據(jù)庫(kù)

3.2 改進(jìn)Apriori 算法數(shù)據(jù)分析

設(shè)置最小支持度0.3 后，由掃描數(shù)據(jù)庫(kù)得到頻繁一項(xiàng)集，如表4 所示。

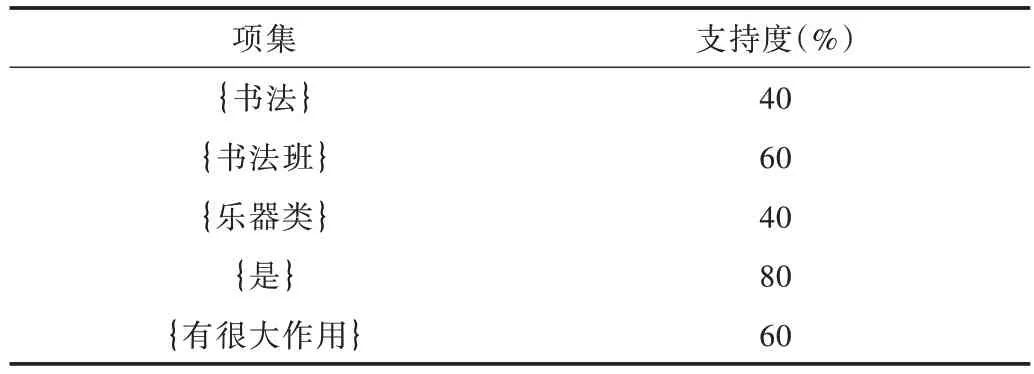
Table 4 Frequent itemsets L1表4 頻繁一項(xiàng)集L1

由于當(dāng)L1不存在需要剪枝的元素即可進(jìn)行連接，通過連接篩選得到L2，如表5 所示。

此時(shí)進(jìn)行剪枝，其元素列表為｛書法，書法班，樂器類，是，有很大作用｝，所有元素均符合約束，所以無剪枝項(xiàng)，連接并篩選得到L3，如表6 所示。

Table 5 Frequent binomial sets L2表5 頻繁二項(xiàng)集L2

Table 6 Frequent trinomial sets L3表6 頻繁三項(xiàng)集L3

再次進(jìn)行剪枝操作，由于｛書法｝的數(shù)量少于3 即可進(jìn)行剪枝，此時(shí)元素列表為｛書法班，樂器類，是，有很大作用｝，連接篩選得到L4：｛書法班，樂器類，是，有很大作用｝。

通過改進(jìn)Apriori 算法，并設(shè)置min_sup為0.40，對(duì)收集到的數(shù)據(jù)進(jìn)行關(guān)聯(lián)規(guī)則分析得出以下頻繁項(xiàng)集，如表7 所示。

Table 7 All frequent itemsets表7 所有頻繁項(xiàng)集

由表7 可知，｛主動(dòng)參加，成果有很大作用｝與｛樂器類，主動(dòng)參加｝屬于頻繁項(xiàng)集，表示學(xué)生主動(dòng)參加并覺得成果有很大作用的概率相對(duì)較大，其具有高置信度，說明學(xué)生在主動(dòng)參加特長(zhǎng)班之后，有很大概率認(rèn)為成果有很大作用。對(duì)于第二個(gè)頻繁項(xiàng)集，亦可用相同思想進(jìn)行分析。

4 實(shí)驗(yàn)結(jié)果

根據(jù)本文的改進(jìn)Apriori 算法思想，將上述數(shù)據(jù)整理分析過程與傳統(tǒng)的Apriori 算法分析過程從數(shù)據(jù)量與運(yùn)行時(shí)間兩方面進(jìn)行對(duì)比。具體說明如下：

（1）測(cè)試環(huán)境：本次測(cè)試采用Python 語言編程，操作系統(tǒng)為Windows 10，處理器為Intel 酷睿i7-6500 雙核處理器，內(nèi)存大小為8GB。

（2）測(cè)試結(jié)果：通過對(duì)2 800 多份問卷進(jìn)行分析，提取特征數(shù)據(jù)，并針對(duì)不同數(shù)據(jù)量進(jìn)行測(cè)試與對(duì)比，得到結(jié)果如圖1 所示。

通過圖1 可以看出，本文提出的改進(jìn)Apriori 算法相比傳統(tǒng)Apriori 算法可以有效縮短運(yùn)行時(shí)間，加快數(shù)據(jù)處理速度。而且隨著數(shù)據(jù)量的增加，算法效果有一定程度提升。

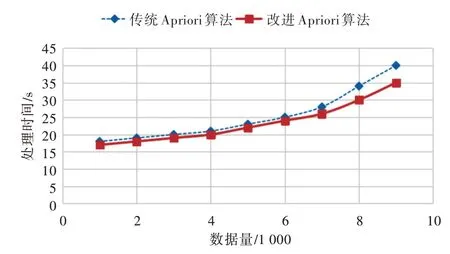
Fig.1 Comparison of running time of each data volume test圖1 各數(shù)據(jù)量測(cè)試運(yùn)行時(shí)間對(duì)比

5 結(jié)語

本文提出的改進(jìn)Apriori 算法主要思想來自于兩個(gè)方面：①改變數(shù)據(jù)庫(kù)結(jié)構(gòu)為項(xiàng)目數(shù)據(jù)庫(kù)結(jié)構(gòu)，傳統(tǒng)的事務(wù)數(shù)據(jù)庫(kù)結(jié)構(gòu)會(huì)造成多次掃描數(shù)據(jù)庫(kù)，帶來很大的時(shí)空開銷［time and memory-consuming］，而采用項(xiàng)目數(shù)據(jù)庫(kù)結(jié)構(gòu)只需掃描一次即可完成整個(gè)算法的運(yùn)行；②根據(jù)算法特性設(shè)計(jì)剪枝操作，相比傳統(tǒng)算法的剪枝操作，在一定程度上能夠提升算法性能。改進(jìn)Apriori 算法在不同數(shù)據(jù)量情況下對(duì)傳統(tǒng)算法的提升效果不同，當(dāng)數(shù)據(jù)量為8 000 時(shí)，改進(jìn)Apriori 算法的運(yùn)行時(shí)間相比傳統(tǒng)算法縮短了7.15%，算法效果得到了相當(dāng)大程度的提升。但不足之處在于當(dāng)數(shù)據(jù)量很大時(shí)，依舊需要大量時(shí)空開銷，其開銷主要存在于剪枝操作中。若能找到更好的剪枝操作方法，則能對(duì)算法作進(jìn)一步改進(jìn)。