純彎梁受壓區聲彈性系數研究

王 毅，楊 予，包 挺，徐 浩

(浙江理工大學 建筑工程學院，浙江 杭州 310018)

近年來，超聲波因其具有方便、快捷、靈敏度高等優點已然成為各類工程中重要的檢測手段[1- 8]。目前，已經有很多學者對超聲波波速與應力之間的關系進行了研究[9- 18]。

由前人研究可知，使用超聲波進行工作應力診斷的關鍵是獲得聲彈性系數，目前對于聲彈性系數的研究集中于軸向拉壓試件，而純彎試件的相關研究較少。考慮到工程中許多構件處于純彎工作狀態，其聲彈性系數顯然具有研究價值。

本文研究了鋼筋混凝土純彎梁受壓區聲彈性系數的獲取方法。具體步驟為：首先，通過純彎梁的加載-聲時測量實驗獲得受壓區表層聲彈性系數；其次，通過素混凝土試件軸壓實驗獲得受壓聲彈性系數；最后，對上述結果進行對比分析，并總結純彎梁受壓區聲彈性系數的獲取方法。

本文首先介紹聲彈性系數理論的發展以及聲彈性計算方法；其次進行純彎梁的加載實驗和素混凝土試件的軸壓實驗；然后對上述聲彈性系數進行對比分析。

1 聲彈性理論

聲彈性理論最早由Murnaghan[19]提出， Hughes等[10]在其研究的基礎上推導了聲彈性系數公式。在之后的研究中，Ivan Lillamand等[11]對Hughes的公式進行了一階簡化，Karen F.Bompan等[12]對比了多個混凝土試件在軸壓狀態下的聲彈性系數。前人研究中常采用如下聲彈性系數公式：

(1)

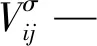
通過測量試件在不同應力狀態下的聲速再結合式(1)可計算出試件的聲彈性系數。

2 實驗過程

2.1 試件制備

為對比鋼筋混凝土純彎梁受壓區和素混凝土受壓試件的聲彈性系數，分別澆筑了一根長寬高規格為1200mm ×100mm×150mm的鋼筋混凝土梁(用于純彎實驗)和一根長寬高規格為550mm×150mm×150mm的素混凝土試件(用于單軸受壓實驗)。兩者在制作時僅尺寸與配筋不同，材料為P.O42.5的普通硅酸鹽水泥，粒徑28～40mm的粗骨料以及普通河砂，配合比見表1。梁的配筋與尺寸如圖1所示，在純彎段僅配置受拉鋼筋以避免受壓區鋼筋對波速測量的干擾，箍筋端頭采用焊接方式相連，鋼筋規格均為HRB400。

表1 混凝土配合比

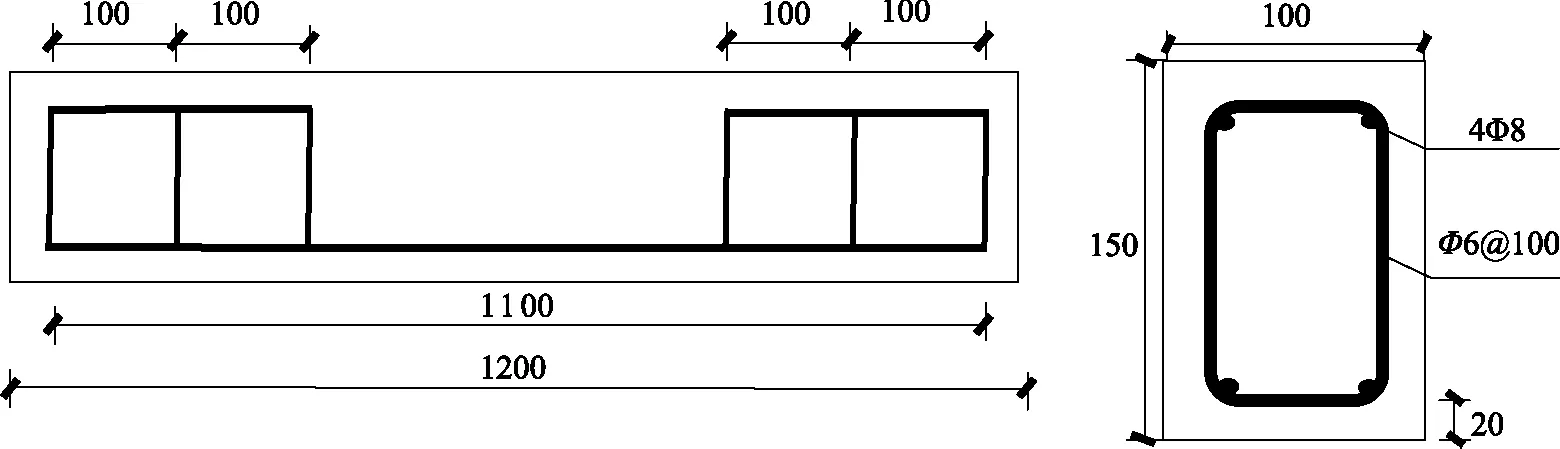
圖1 梁的配筋與尺寸

2.2 實驗裝置

實驗裝置照片如圖2所示。在純彎實驗中，采用圖2(a)所示裝置加載測量波速，加載裝置由短型30t千斤頂與CP- 700液壓泵構成，荷載由分配梁傳給純彎梁，采用YE2533程控讀數儀控制液壓泵施加的荷載。在單軸受壓實驗中，采用圖2(b)所示裝置加載測量波速，圖中液壓機為YAR- 2000微機控制電液伺服壓力試驗機。

圖2 實驗裝置照片

2.3 測點布置

為測量試件在不同應力狀態下的波速，鋼筋混凝土梁純彎實驗在受壓區上方布置了2個40kHz換能器，如圖3所示，換能器中心距為400mm。素混凝土試件單軸受壓實驗在試件側面布置了2個40kHz換能器，如圖4所示，換能器中心距也取為400mm。

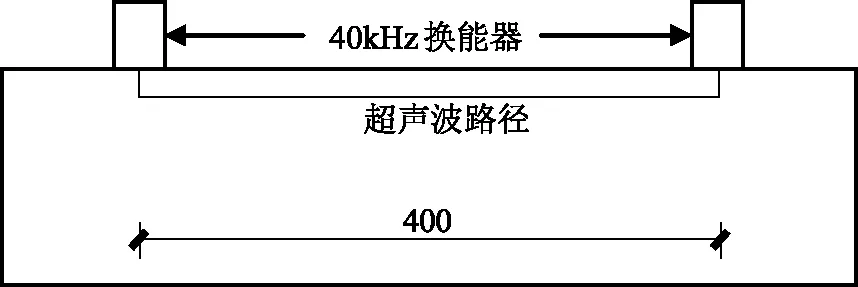
圖3 純彎實驗測點布置圖

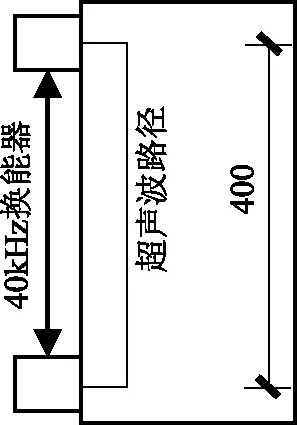
圖4 軸壓實驗測點布置圖

2.4 加載與讀數

鋼筋混凝土梁純彎實驗采用四點彎方式加載，通過裂縫觀測儀觀察并控制梁表面最大裂縫寬度≤0.3mm以保證整個加載實驗梁處于正常工作極限狀態以內。荷載為6個等級：3000、6000、9000、12000、15000、18000N。為減少實驗中微裂縫擴展對波速測量造成的影響，在測量聲時前對梁進行了3輪預加載，然后再進行3輪分級加載，每級荷載穩定后測量記錄聲時，加載過程如圖5(a)所示。

素混凝土試件單軸受壓實驗利用電腦控制液壓機以1kN/s的速率對試件施加總共6個等級的荷載，每級應力增量為1MPa，最大應力為6MPa。加載過程分3輪預加載和3輪循環加載，每級荷載穩定后測量記錄聲時，如圖5(b)所示。

實驗數據處理方法借鑒規范CECS02：88《超聲回彈綜合法檢測混凝土強度技術規程》，即每一級荷載的聲時均讀取并記錄16個數據，去掉最大和最小的3個數據，取剩余數據的平均值作為該級聲時，再結合測距計算出波速。

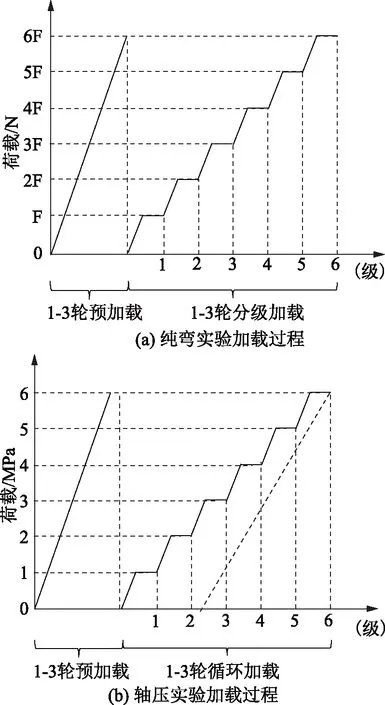
圖5 實驗加載過程圖

圖6 純彎聲彈性系數

3 實驗結果與對比分析

3.1 純彎梁受壓區聲彈性系數

根據純彎梁實驗中測得的波速和式(1)可計算出聲彈性系數。圖6為聲彈性回歸系數圖，x軸為根據平截面假定求出的受壓側混凝土應力，y軸為波速變化率。

圖6中擬合出的直線斜率即為純彎梁受壓區聲彈性系數，第三輪實驗結果比前兩輪小，其原因是前兩輪加載過程中不斷產生新的微裂縫。考慮到第三輪實驗時梁的微裂縫基本穩定，受彎聲彈性系數取為第三輪循環加載實驗結果0.342(%/MPa)。

3.2 單軸受壓試件聲彈性系數

圖7為依據單軸受壓實驗結果繪制的聲彈性系數回歸分析圖。

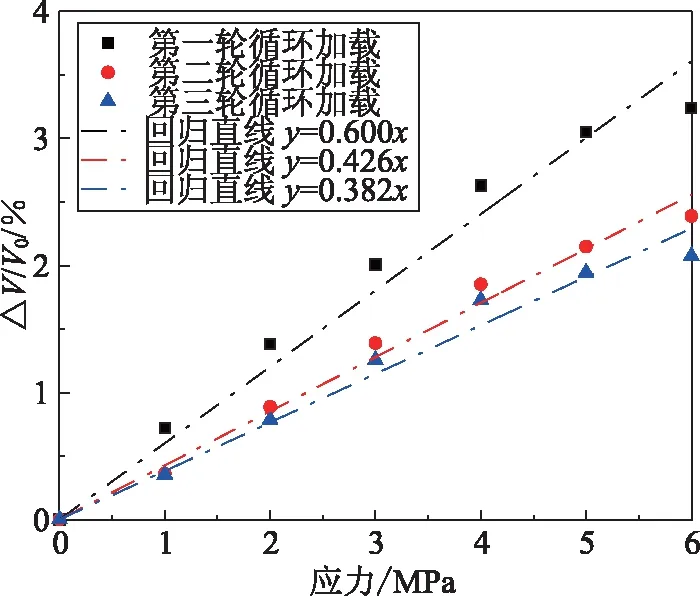
圖7 受壓聲彈性系數

由圖7可知，多輪循環加載實驗得到的受壓聲彈性系數與前人[9- 10]的研究結果接近。由于軸壓實驗在前兩輪加載過程中新微裂縫發展速度較快，故受壓聲彈性系數取為第三輪實驗結果0.382(%/MPa)與純彎梁受壓區聲彈性系數0.342(%/MPa)非常接近。

3.3 兩種聲彈性系數的對比分析

純彎梁受壓區聲彈性系數與素混凝土試件受壓聲彈性系數對比如圖8所示。由圖8可知，兩種聲彈性系數在0.3～0.6(%/MPa)之間，受彎聲彈性系數的最終取值為0.342(%/MPa)比受壓聲彈性系數0.382(%/MPa)小0.04(%/MPa)，考慮到實驗中操作以及儀器測量等原因帶來的誤差很難完全避免，這兩個聲彈性系數的差值在可接受誤差范圍之內。

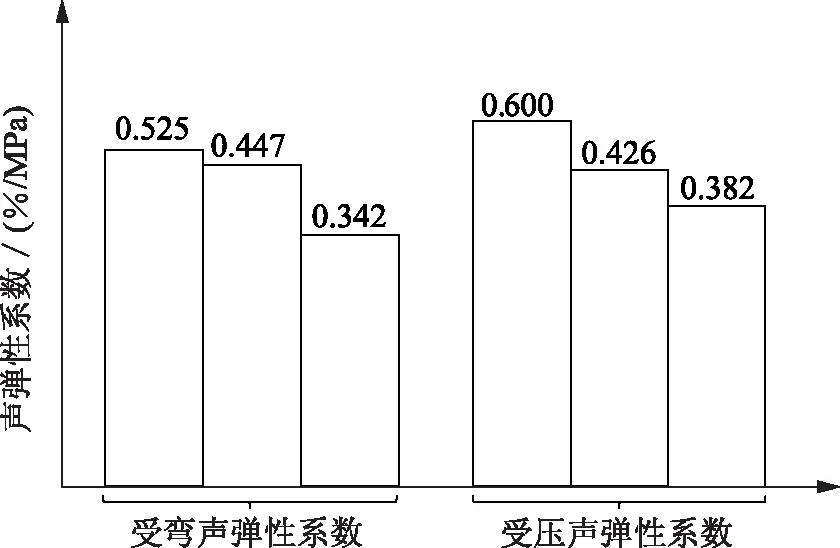
圖8 聲彈性系數對比

4 結論

本文通過多輪循環加載實驗測量了兩根試件(僅尺寸與配筋不同)處于不同應力狀態下的波速，并依據聲彈性理論擬合出聲彈性系數。實驗結果表明，受壓聲彈性系數為0.382(%/MPa)比受彎聲彈性系數0.342(%/MPa)大0.04(%/MPa)，兩種聲彈性系數的差值在可接受范圍之內。

結論為可通過測量素混凝土試件的受壓聲彈性系數來確定純彎梁受壓區的聲彈性系數，測試中采用的條件應保持一致性。

本文僅對受彎及受壓狀態下的聲彈性系數進行了研究，而試件處于其他受力狀態(例如受拉、偏心受壓等)時的聲彈性系數是否可以采用類似方法測定，需要后續實驗進行補充完善。