行波波長及波速對獲能特性的影響

張繼化，孫曉晶，黃典貴

（上海理工大學 能源與動力工程學院，上海 200093）

魚類經過億萬年的進化，逐漸擁有了很強的游動能力，不僅具有很高的游動效率，還具有極強的機動性能。因此，人類對魚類游動進行了大量的研究，1936年Gray通過實驗觀測提出了著名的“Gray 疑題”。他發現同樣航速的直體海豚模型所消耗的能量約是活體海豚的七倍，故推測活體海豚通過某種方式減小了阻力。

在理論研究方面，Lighthill將波動推進細分為3種方式，并提出了用于鲹科推進模式的細長體理論，認為運動獲得的反作用力只與瞬時加速度有關；Wu給出了二維波動模型，加入了前緣吸力及尾緣尾跡的作用，系統地發展了二維波動板理論，為三維波動板理論的提出奠定了基礎。

在實驗研究方面，借助先進的數字式粒子圖像測速技術（DPIV），Wolfgang等測量鮐魚游動時的二維流場結構發現，在游動過程中，在魚體兩側產生渦，向后運動至尾柄處脫落，這些脫落渦被尾鰭利用，可以降低能量消耗；Barrett等對機器魚進行實驗，討論了模型中魚體波動波長、波動振幅和Strouhal數等參數對阻力降低的影響。

在數值模擬方面，Borazjani等對鯖魚進行了數值模擬，指出雷諾數對鲹科類游動的水動力性能具有重要影響，給出了鯖魚的三維尾渦流場結構，研究表明影響流場結構的因素主要是Strouhal數；Dong等分析了一排無窮多個波動翼形的非定常黏性繞流問題，結果表明，反相擺動有助于增強推進力，同相擺動有利于節省游動的能耗。

魚類使自己的身體產生行波運動，將能量施加給水，產生反卡門渦街的尾流結構，自身獲得推力而前進。相反地，Huang等通過數值模擬發現，在流動的水中魚體作不等振幅的行波運動，當無量綱波速小于一定值時，魚體表面單元壓力差方向和速度方向相同，水對魚體做正功，即魚體從水流中獲得能量，產生卡門渦街的尾流結構。這種全新的獲能模式，為未來機器魚的超遠距離航行提供了理論基礎。為了進一步研究不同參數下魚體獲能的規律，本文從二維魚體作等振幅的行波運動入手，改變行波運動的波長和無量綱波速，研究這兩個參數對獲能特性的影響。

1 物理模型和數值方法

1.1 物理模型

本文以NACA0012翼型作為魚體二維的原始簡化模型，在水流中作行波運動，示意圖如圖1所示，其中：

x

、

y

分別為笛卡爾坐標系的橫、縱坐標；

y

(

x

,

t

)為

t

時刻模型上點的縱坐標；

λ

為行波波長；

A

為最大振幅；

U

為來流速度。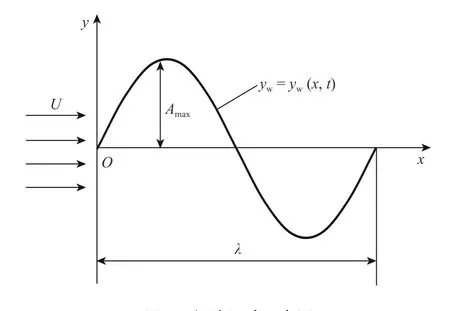

圖1 行波運動示意圖Fig. 1 Schematic diagram of traveling wave motion

在行波運動過程中，給定行波波長和最大振幅，在保證中弧線長度不變的情況下，運動形式是唯一的，因此波動方程可以表示為

式中：

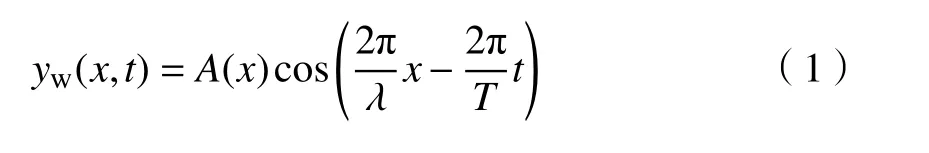
T

為波動周期；

A

(

x

) 為振幅函數。

本文研究等振幅的情況，故振幅函數可以表示為

式中：

c

為振幅系數；

L

為中弧線長度。行波運動的波速以來流速度

U

對其無量綱化，得到無量綱波速

c

，即

1.2 側向功率和能量利用率

魚體波動所受的力主要由摩擦力和壓差力組成。摩擦力來自于模型表面的黏性剪切力，壓差力來自于模型表面流體的壓力差，作用在

y

方向微元的分量和有量綱表達式為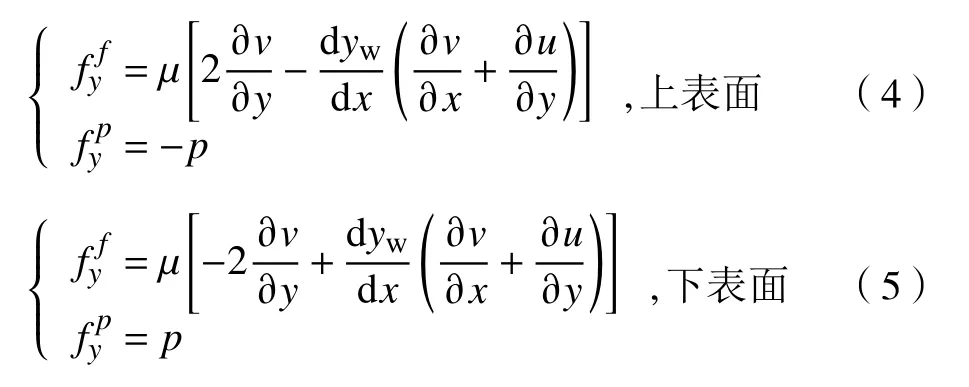

式中：為摩擦力的

y

方向分量；為壓差力的

y

方向分量；

u

為

x

方向速度；

v

為

y

方向速度；

μ

為流體動力黏度；

p

為微元表面壓力。速度在

y

方向的分量表達式為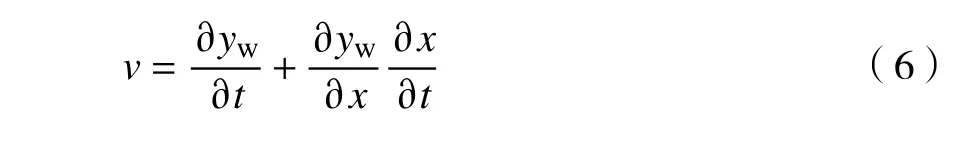

因此魚體從水中獲得的側向功率為

式中：

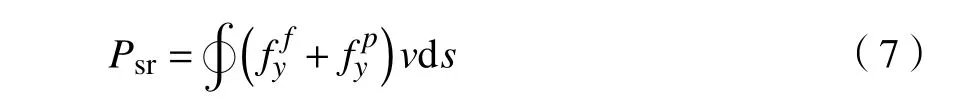
P

為側向功率（獲得的能量）；d

s

為微元面積。將

P

以

ρU

L

無量綱化，得到無量綱側向功率

P

。

定義最大可以獲得的來流能量為

式中：

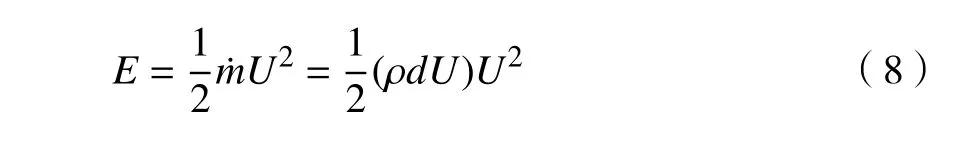
E

為來流能量；為質量流量；

ρ

為水的密度；

d

為最大掃掠高度。

于是定義能量利用率為

式中，為能量利用率。

2 數值模擬

2.1 網格和數值計算

使用ICEM CFD劃分網格，網格數為375194，翼型表面生成邊界層網格，動網格域采用三角形的非結構網格，之外的計算域采用結構網格。進、出口邊界條件分別設置為速度進口和壓力出口，翼型表面設置為固體壁面。網格整體視圖和邊界層局部放大圖如圖2所示。數值模擬采用Fluent軟件計算，介質為水，采用壓力基求解，選用S-A模型，動網格采用光順和重構這兩種方法。模擬計算時，先預處理1個周期，使對稱翼型逐漸變至初始時刻位置。

圖2 計算網格Fig. 2 Grid details

2.2 計算方法驗證

Nishio等通過實驗測量了不同相位落后角下巡游推進時魚體所受的阻力。阻力測量的實驗裝置如圖3所示。該實驗模型為三維模型，截面為NACA0018，弦長為0.15 m，細長比為1∶6。模型放置于循環水槽中，浸沒部分長度為0.2 m。模型被固定在1/4弦長處，身上共有4個關節，通過計算機控制每個節點的運動，給定周期2 s，改變相位落后角。在實驗過程中，電機沿水平方向拖動模型，由施加載荷測出該方向的推力，當水平方向合力為0時，阻力和推力大小相等，方向相反，此時模型達到巡游，巡游速度為0.35025 m·s，那么施加在模型上的載荷力就是所受的阻力。

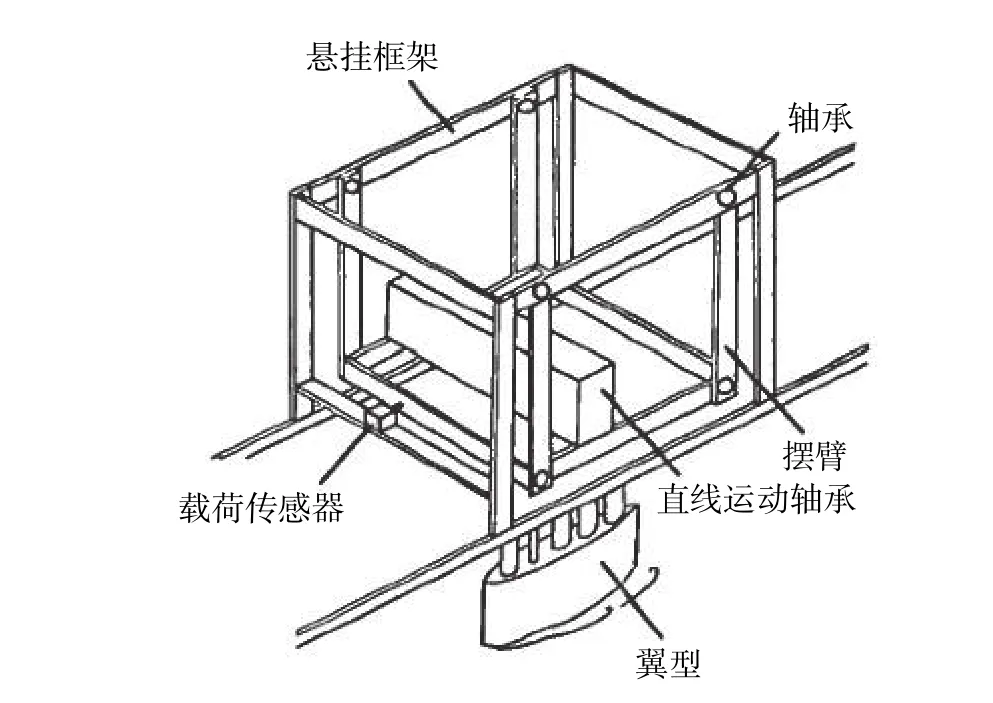
圖3 阻力測量的實驗裝置［13]Fig. 3 Experimental set-up of the hydrodynamic force measurement［13]

為了驗證數值模擬方法的可靠性，本文采用Nishio的實驗工況參數和運動方式，模擬計算了原始翼型為NACA0018的二維柔性體在水中巡游推進時的阻力系數，并與Nishio的實驗結果進行了比較。其中，計算時間步長為0.002 s，每個周期計算1000步，總共計算6個周期，就阻力系數和運動相位落后角的關系與參考文獻中的實驗值進行了對比，結果如圖4所示，其中：

C

為阻力系數；

φ

為相位落后角。

從圖4中可以看出，二維模擬計算得到的阻力系數與相位落后角的整體趨勢與實驗值的十分接近。但與文獻的實驗值相比，本文得到的阻力系數在相位落后角較小時偏差大，在大相位落后角時偏差小。從總體上來看，本文所采用的網格和計算程序的可靠性和可信性得到了驗證。

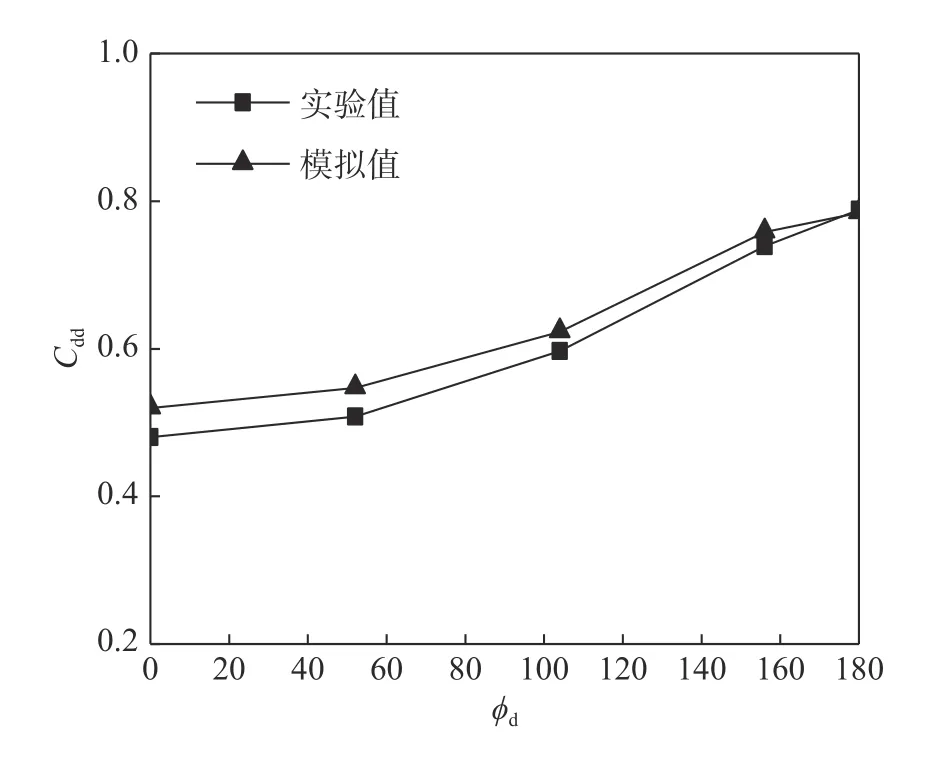
圖4 數值模擬值與實驗值對比［12-13]Fig. 4 Comparison between numerical simulation results and experimental ones［12-13]

3 計算結果及分析

本文取雷諾數

Re

= 120000，其中特征速度為來流速度

U

= 1 m·s，特征長度為中弧線長度，

L

= 0.12 m，給定最大振幅

A

=

c

L

= 0.1

L

=0.012 m，研究不同的行波波長和波速對獲能特性的影響。圖5為模型在1個周期內4個時刻所在位置與形狀。圖6給出了在不同行波波長

λ

下，無量綱側向功率

P

隨無量綱波速

c

的變化。由圖中可以看出，隨著無量綱波速

c

增大，無量綱側向功率

P

先增大后減小，并存在一個最佳的無量綱波速，當

c

在0.5附近時，使得無量綱側向功率

P

最大；當無量綱波速

c

大于1時，側向功率小于0，此時行波運動將處于推進區，即魚類游動時，無量綱波速

c

大于1，此時無法從流水中獲得能量。行波能夠從流體中獲能的無量綱波速區間大致為0～1。圖7給出了在不同行波波長

λ

下，能量利用率

η

隨無量綱波速

c

的變化。由圖中可以看出，能量利用率

η

的變化規律和無量綱側向功率

P

相同。隨著無量綱波速

c

的增大，能量利用率

η

先增大后減小，并存在一個最佳的無量綱波速，當

c

在0.5附近時，使得能量利用率

η

最大。在所研究的范圍內，當

λ

= 0.6

L

、

c

= 0.5時，能量利用率達到最大值28.35%。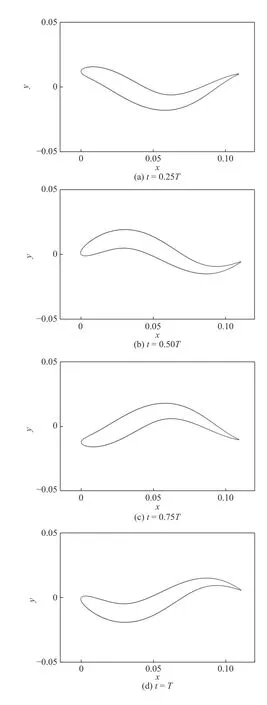

圖5 1個周期內模型在4個時刻所在位置與形狀Fig. 5 Schematic diagram of the model at four moments of one cycle

圖6 無量綱側向功率與無量綱波速和行波波長的關系Fig. 6 Relationship among dimensionless power output,dimensionless wave velocity, and wavelength

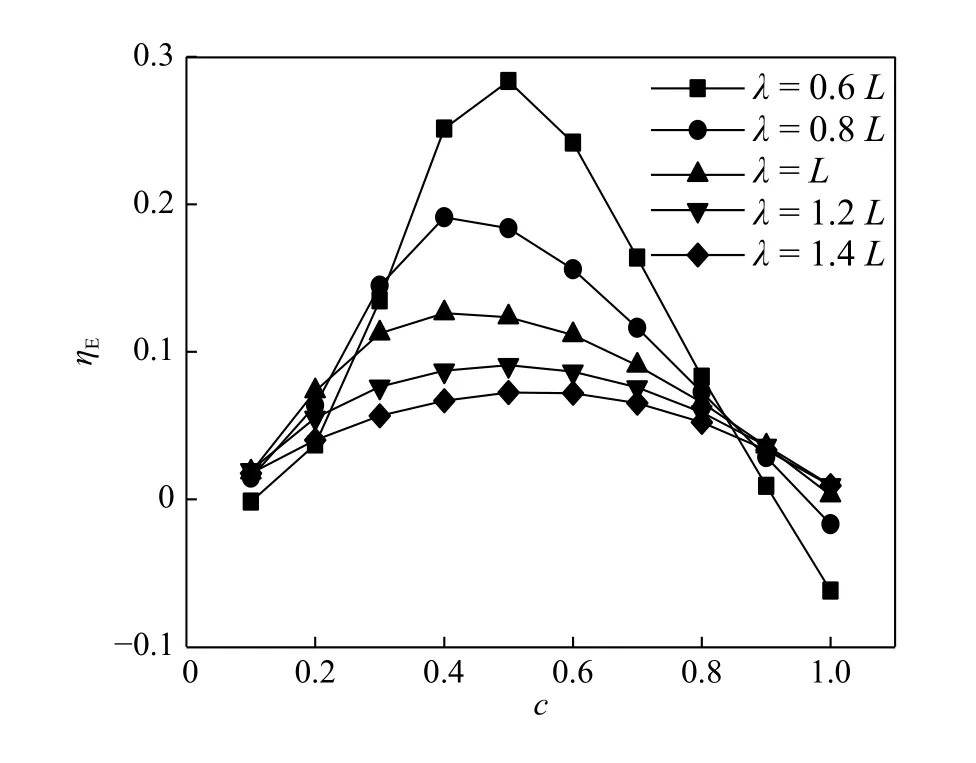
圖7 能量利用率與無量綱波速和行波波長的關系Fig. 7 Relationship among energy extraction efficiency,dimensionless wave velocity, and wavelength

圖8給出了行波波長

λ

=

L

時不同無量綱波速下的渦量云圖。從圖中可以看出，隨著無量綱波速的增大，渦脫落的頻率相應增大。當

c

較小時，波動頻率較小，渦脫落較慢，流道形成阻塞，故能量利用率較低；當

c

較大時，波動頻率較大，渦脫落較快，壁面附面層變薄，壓差減小，故能量利用率也較低；當

c

= 0.5時，正好在尾跡區形成卡門渦街，能量利用率達到最大值。圖9給出了在不同的無量綱波速

c

下，能量利用率

η

隨無量綱波長

λ

/

L

的變化。由圖中可以看出，在所研究的范圍內

c

處于不同的區間段時，

η

的變化規律也不相同。當

c

較小，即處于低無量綱波速區時，隨著無量綱波長

λ

/

L

的增大，

η

先增大后減小；當

c

在0～1中間區段，即處于中無量綱波速區時，

η

隨著無量綱波長

λ

/

L

的增大而逐漸減小；當

c

較大，即處于高無量綱波速區時，隨著無量綱波長

λ

/

L

的增大，

η

先增大后減小。

圖8 定行波波長(λ = L)下不同無量綱波速時的渦量云圖 Fig. 8 Vorticity contours for different dimensionless wave velocities at λ = L

圖9 不同無量綱波速下能量利用率隨無量綱波長的變化Fig. 9 Variations of energy extraction efficiency with dimensionless wavelength at different dimensionless wave velocities

圖10給出了無量綱波速

c

= 0.5時不同行波波長

λ

下的壓力云圖。從圖中可以看出：魚體尾跡存在較大的低壓區，這意味著水中的能量被魚體吸收，使魚做功；當

λ

= 0.6

L

時，尾跡中的低壓區最大，連成一片，表明魚體從水中獲取的能量最多；隨著行波波長的增大，魚體尾跡負壓區面積逐漸減小，表明魚體從水中吸收能量的能力逐漸下降。

圖10 定無量綱波速(c = 0.5)下不同行波波長時的壓力云圖Fig. 10 Pressure distribution for different wavelengths at c = 0.5

4 結論

本文以原始翼型NACA0012作為魚體二維簡化模型，使用商業軟件Fluent進行數值模擬，研究了行波波長

λ

和無量綱波速

c

對無量綱側向功率

P

和能量利用率

η

的影響。

在一定參數范圍內，魚體的行波運動具有從流動的水中獲取能量的能力，具體結果為：

(1) 行波波長一定時，無量綱側向功率與能量利用率隨無量綱波速先增大后減小，并存在一個最佳波速；

(2) 對于不同的行波波長，最佳無量綱波速均出現在

c

= 0.5附近，其對應的最大無量綱側向功率和能量利用率隨著行波波長的增大而減小，當

λ

= 0.6

L

、

c

= 0.5時，能量利用率達到最大值28.35%；(3) 在所研究的范圍內，當無量綱波速

c

處于中波速區時，

η

隨著無量綱波長

λ

/

L

的增大而逐漸減小。當無量綱波速

c

處于低波速和高波速區時，隨著無量綱波長

λ

/

L

的增大，能量利用率

η

先增大后減小；

(4) 獲能和耗能的臨界無量綱波速基本不隨行波波長的變化而變化，獲能區間大致在0～1之間。