DFIG網側變換器反饋線性化與滑模控制

侯傳羽，李嵐，趙楠，楊琦，楊旭

(太原理工大學電氣與動力工程學院，太原030024)

0 引言

隨著近年來風能設施的進步，風能作為可再生能源，愈來愈具有經濟競爭力和發展潛力[1 - 3]。而目前主流的風電機組通常采用變速恒頻機組，以雙饋異步發電機(doubly fed induction generator, DFIG)組為主，其定子直接掛接電網，轉子通過三相交—直—交變換器實現交流勵磁，可以通過定子、轉子雙通道實現電功率的交換。轉子勵磁變換器常采用背靠背三相兩電平電壓型PWM變換器，兩PWM變換器按照其所在位置分別為網側變換器(grid-side converter, GSC)和轉子側變換器(rotor-side converter, RSC)[4]。DFIG有超同步，亞同步，同步三種工作狀態，本文研究的是GSC在整流工況實現功率因數控制，即亞同步狀態。當DFIG處于亞同步時，需要GSC向DFIG供電，若電網發生不對稱故障時，網側將出現二倍頻交流量，最終將會傳遞至轉子側，嚴重危害DFIG風電機組的機械系統安全，故在DFIG系統中，對GSC的控制尤為重要。

目前GSC的控制通常采用同步旋轉坐標系下雙環級聯PI控制。在PI控制器下，GSC的控制雖然容易實現，但動態性能不是很理想，其中電流電壓很難進行快速跟蹤，因此想要達到理想的控制效果非常困難。

對于結構復雜，強耦合的非線性系統，經典控制理論很難對系統內部的變化做出描述，而基于微分幾何的現代控制理論能夠從系統的內部狀態出發，充分描繪系統全部的動態過程。GSC本質也是一種變換器，從現代控制理論的角度，國內外也進行了研究，提出了一些相應的非線性控制理論。文獻[5]提出電壓外環使用滑模控制(sliding mode control，SMC)，但其SMC是基于穩態的滑模面，并不具備良好的動態性能；電流內環使用反饋線性化控制(feedback linearization, FL)，由于控制量的電流參考值在同步旋轉坐標系下為常數，微分后為0，且引入了耦合項，最后化簡的控制器的表達式和雙環級聯PI控制并無差異。文獻[6]在不平衡電網下使用含有滑模補償的反饋線性化控制，在dq坐標系中該控制的電流環將產生4個變量系數，再加上電壓環的變量系數，調節難度極大。文獻[7]使用FL直接電壓控制，也是基于同步旋轉坐標系，但因為存在直流母線電壓的二階微分，運算過程極為繁瑣。

以上的控制方法相較于傳統的PI控制方式，都改善了系統的動態性能，但是它們都有一個相同點：通過基于旋轉同步坐標下反饋線性化控制律，這種控制方式不僅需要電網電壓定向，還會出現與傳統PI相同的控制結構[8 - 13]，甚至在不平衡電網下，增加控制的復雜性[14]。在總結前述文獻成果的基礎上，論文在理想電網下建立靜止坐標系下的反饋線性化控制數學模型，這種方法避免了在同步旋轉系下與傳統PI控制相一致的情況，并且減少了因旋轉因子帶來的耦合項。通過增加含飽和函數的滑模控制，進一步提高動態性能，以實現網側功率因數控制和電壓穩定的目的。最后通過仿真驗證上述控制方法的正確性。

1 靜止坐標系下GSC數學模型

圖1為GSC的結構框圖。

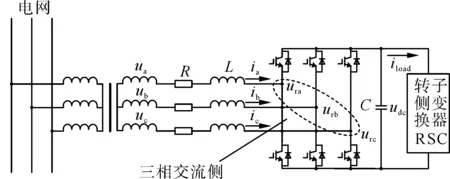
圖1 GSC結構框圖Fig.1 Topology of grid side converter

圖1中ua、ub、uc為變壓器輸出電壓；ura、urb、urc為網側變流器交流側電壓；R為寄生電阻，L為濾波電抗器的電感；ia、ib、ic為網側變流器輸入電流；C為直流母線濾波電容；udc為直流母線電壓；iload為網側流向轉子變流器的電流。

三相靜止abc坐標系下數學模型為：

(1)

根據GSC的拓撲結構，結合式(1)可得在兩相靜止αβ坐標系下的數學模型為：

(2)

(3)

2 GSC電流內環控制器設計

2.1 系統相對階

對于y1=iα=x1=h1(x)，根據式(3)可得：

(4)

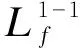
同理，對于y2=iβ=x2=h2(x)，可得：

(5)

(6)

由式(4)和(5)初步判斷γ1=1，γ2=1(γ1為y1=h1(x)對應的子相對階，γ2為y2=h2(x)對應的子相對階)；通過式(6)可知為非奇異，則由此判定系統式(3)的相對階γ=γ1+γ2=2，即γ=n(n為系統的階數)。

2.2 FL控制律的確定

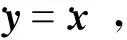
(7)

則：

(8)

即：

(9)

由式(9)可得FL控制律為：

(10)

式中v1、v2為新的控制輸入。

通過FL控制律式(10)，可得輸出與新的輸入關系為：

(11)

為了實現跟蹤控制，新的輸入由下式確定。

(12)

式中：y1_ref=iα_ref；y2_ref=iβ_ref；e1=iα_ref-iα,e2=iβ_ref-iβ；iα_ref和iβ_ref均為參考電流。

其誤差動態方程為：

(13)

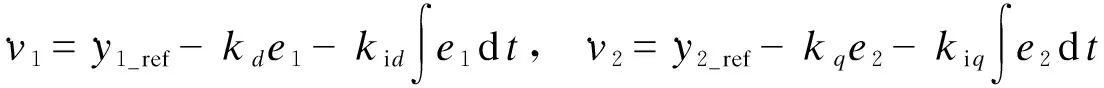
把式(12)代入式(10)可得：

(14)

又因為u1=uα-urα，u2=uβ-urβ，則GSC調制所需的合成期望電壓為：

(15)

3 GSC電壓外環控制器設計

選取滑模面函數[15 - 18]為：

S=udc_ref-udc

(16)

式中udc_ref為直流母線電壓參考值。

通過選擇合適的指數趨近律來限定滑模控制趨近階段的運動軌跡以保證系統趨近運動的動態品質。由于系統在滑模面可能出現高頻抖動，本文選用飽和函數sat(S)替換傳統的sgn(S)來削弱其高頻抖動，則指數趨近律如式(17)—(18)所示。

(17)

(18)

式中：k1、k2為滑模控制器參數，且k1>0，k2>0；ε為誤差帶，ε>0。

當系統穩定時，系統的直流母線電壓udc將無靜差跟蹤參考值udc_ref，所以有：

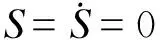
(19)

將式(19)代入到式(16)中，可得：

(20)

又由直流母線電壓與功率關系，可得內環有功功率與直流母線電壓關系為：

(21)

結合式(17),式(20)—(21)，可得網側變換器直流母線電壓外環的控制方程為：

p=(C[k1S+k2sat(S)]+iload)udc

(22)

綜上，可得到GSC控制框圖如圖2所示。

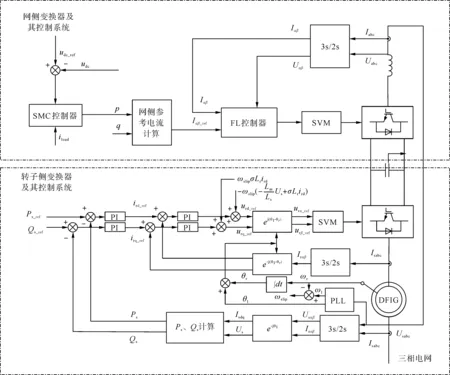
圖2 DFIG網側、轉子側變換器聯合控制原理圖Fig.2 DFIG grid-side and rotor-side converter combined control schematic diagram

4 穩定性分析

定義Lyapunov函數為：

(23)

對式(23)求導，可得：

(24)

當|S|>ε時，有：

sat(S)=sgn(S)

(25)

將式(25)代入到式(24)，可得：

(26)

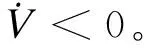
當|S|≤ε時，有：

(27)

將式(27)代入到式(24)，可得：

(28)

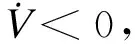
5 GSC參數設計

5.1 GSC網側電感的設計

若忽略GSC網側電阻R，穩態條件下，GSC網側矢量關系如圖3所示，且只考慮基波正弦電量。

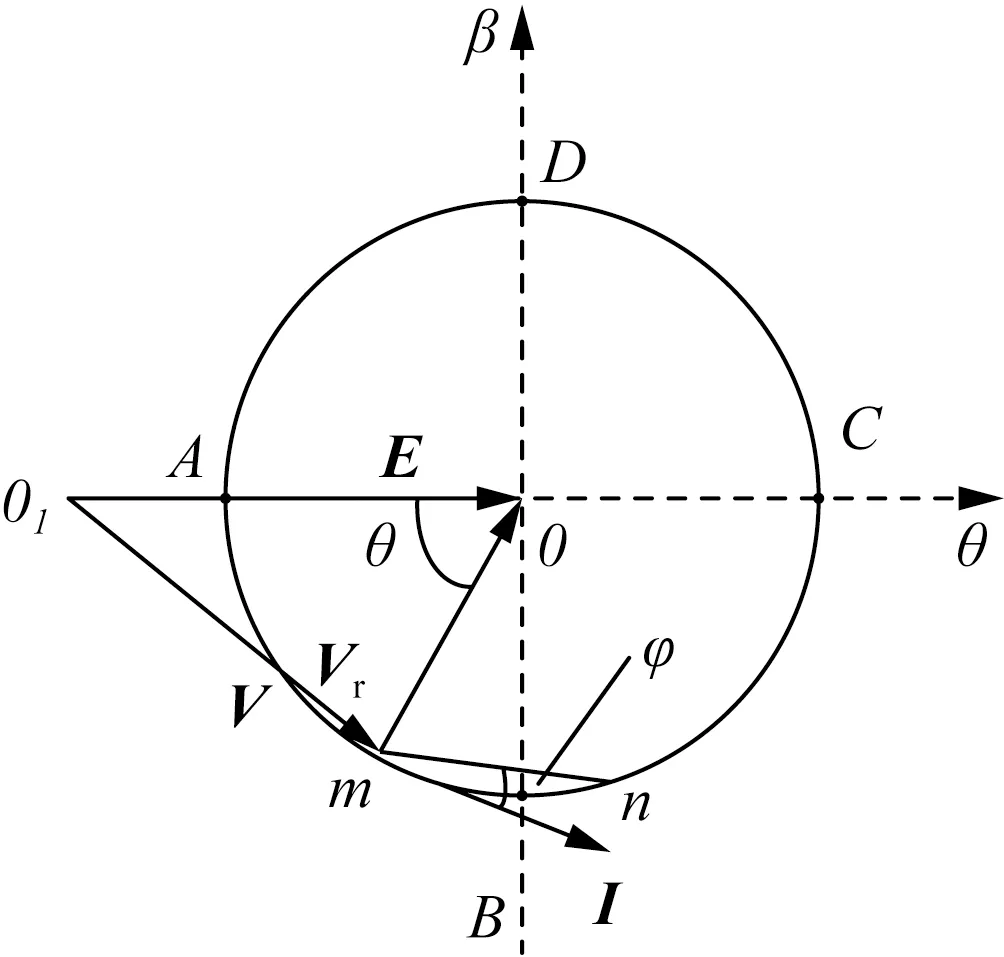
圖3 GSC網側穩態矢量關系Fig.3 Steady-state vector of relationship GSC AC side

對圖3中所示三角形，由余弦定理可知：

|V|2=|E|2+|Vr|2-2|E||Vr|sinφ

(29)

由GSC網側電感的伏安關系式|Vr|=ωL|I|，代入式(29)，化簡得

(30)

式中：E為網側變壓器電動勢矢量；V為GSC網側相電壓矢量；Vr為GSC網側電感電壓矢量；I為GSC網側相電流矢量。

因為：

|V|max=ηudc

(31)

式中：η為PWM相電壓最大利用率。

即：

|V|≤ηudc

(32)

將式(32)代入式(30)，得GSC網側電感為：

(33)

由式(33)可得：

(34)

GSC采用SVPWM控制，且忽略GSC損耗，則有：

(35)

式中：p為GSC交流側有功功率；q為GSC交流側無功功率。

滿足單位功率因數下，將式(35)代入式(33)可得：

(36)

然而根據實際情況網側電感都帶有寄生電阻，考慮網側電阻時的GSC網側矢量關系如圖4所示。其中虛線矢量是忽略電阻影響時的GSC網側電壓矢量V′，實線矢量則是考慮電阻影響時的GSC網側電壓矢量V。

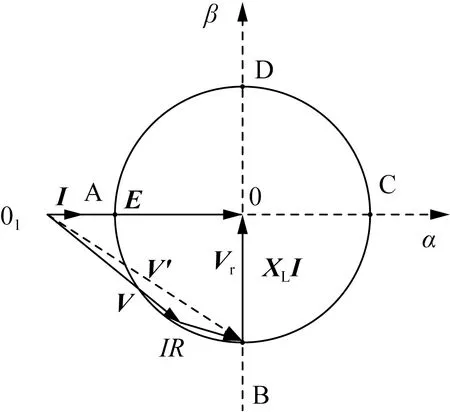
圖4 GSC網側電阻對其網側電壓矢量的影響Fig.4 The influence of GSC AC grid side resistance on AC side voltage vector

如圖4所示，GSC工作在單位功率因數下，由于|V′|>|V|，因此當考慮GSC網側電阻影響時，GSC交流側基波電壓幅值有所減小，在相同條件下運行時，GSC網側電感上限值應相應增大。

5.2 GSC直流側電容的設計

當GSC直流電壓給定為直流電壓參考值時，電壓調節器采用滑模控制器，則在GSC實際直流電壓未超過參考值之前，滑模控制器的輸出將會向滑模面趨近。由于滑模控制器輸出為GSC網側功率參考值，在給定直流電壓下，此時GSC直流側將以最大電流Idm對直流電容及負載充電，從而使GSC直流電壓以最快速度上升。這動態過程等效電路如圖5所示。

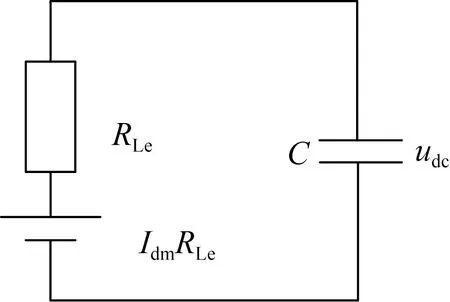
圖5 GSC直流電壓躍變時等效恒壓源電路Fig.5 Equivalent constant voltage source circuit when GSC DC voltage jumps

由圖5易知：

(37)

式中：RLe為轉子側等效負荷電阻；Idm為最大電流；τ1為時間常數。

化簡得：

(38)

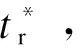
(39)

6 關于轉子側PWM變換器及其影響

由于直流環節的解耦作用，DFIG系統中的各變換器功能相互獨立，其中GSC主要控制直流側穩定以及獲得良好的交流輸入性能，并不會直接參與對DFIG進行控制；RSC則是用以實現DFIG及其整個雙饋風力發電系統的運行控制，其控制的有效性將直接影響DFIG風電系統的運行性能。

在保證GSC控制直流側穩定情況下，為了保證最大風能跟蹤，根據其原理，在不計機械損耗的條件下，DFIG輸出總電磁功率參考值由文獻[19]可知：

(40)

式中：Popt為最佳功率；ωm為發電機轉速；ωr為風力機轉速；np為DFIG極對數；N為齒輪箱增速比；Pe_ref為總電磁功率參考值；Kw是與風力機有關的常數。

根據總電磁功率與定子有功之間關系，可以得到定子輸出有功參考值Ps_ref，即：

(41)

式中：Pcus為定子銅耗；s為DFIG運行轉差率。

通過式(41)并對定子輸出有功進行閉環控制，進而實現對總電磁功率的有效控制，控制原理圖如圖2所示。

7 仿真分析

為了驗證本文所述控制策略的有效性，在MATLAB/Simulink環境中對其所述控制策略進行仿真。GSC仿真的主要參數按照上文參數要求，設計如下：變壓器輸出線電壓190 V/50 Hz；交流側濾波電感10 mH；電阻5 Ω；直流側初始電壓為0，參考電壓220 V；直流側電容470 μF；負載為RSC；ipm開關頻率為10 kHz。圖6為仿真結果。

圖6(a)和圖6(b)為靜止坐標系下網側參考電流和實際電流，實際電流能夠較好地跟蹤參考電流；圖6(c)上半圖為傳統雙環級聯PI控制下的iα、iβ波形，下半圖為外環為滑模控制，內環為FL控制下的iα、iβ波形，對比可知，傳統控制方式下的iα、iβ具有很明顯的超調，而在非線性復合控制方式下的動態過程過渡非常平滑；圖6(d)上半圖為外環使用PI控制內環為FL控制下的iα、iβ波形，下半圖為外環使用滑模控制器，內環使用FL控制下的iα、iβ波形，如圖6(d)所示，在0.01 s使用非線性復合控制的6(d)超調更小，動態性能更好。圖6(e)為非線性復合控制下的三相輸入電壓和網側電流波形，圖中三相輸入電壓和網側電流同相位，實現了單位功率因數控制。圖6(f)和圖6(g)分別為傳統控制下的直流母線電壓udc和非線性復合控制下的直流母線電壓udc，通過兩圖對比可知，傳統控制下的udc在0.05 s前具有很大的超調，在0.13 s才趨于穩定，而非線性復合控制下的udc并沒有超調，且在0.025 s就達到穩態，具有很好的快速性。

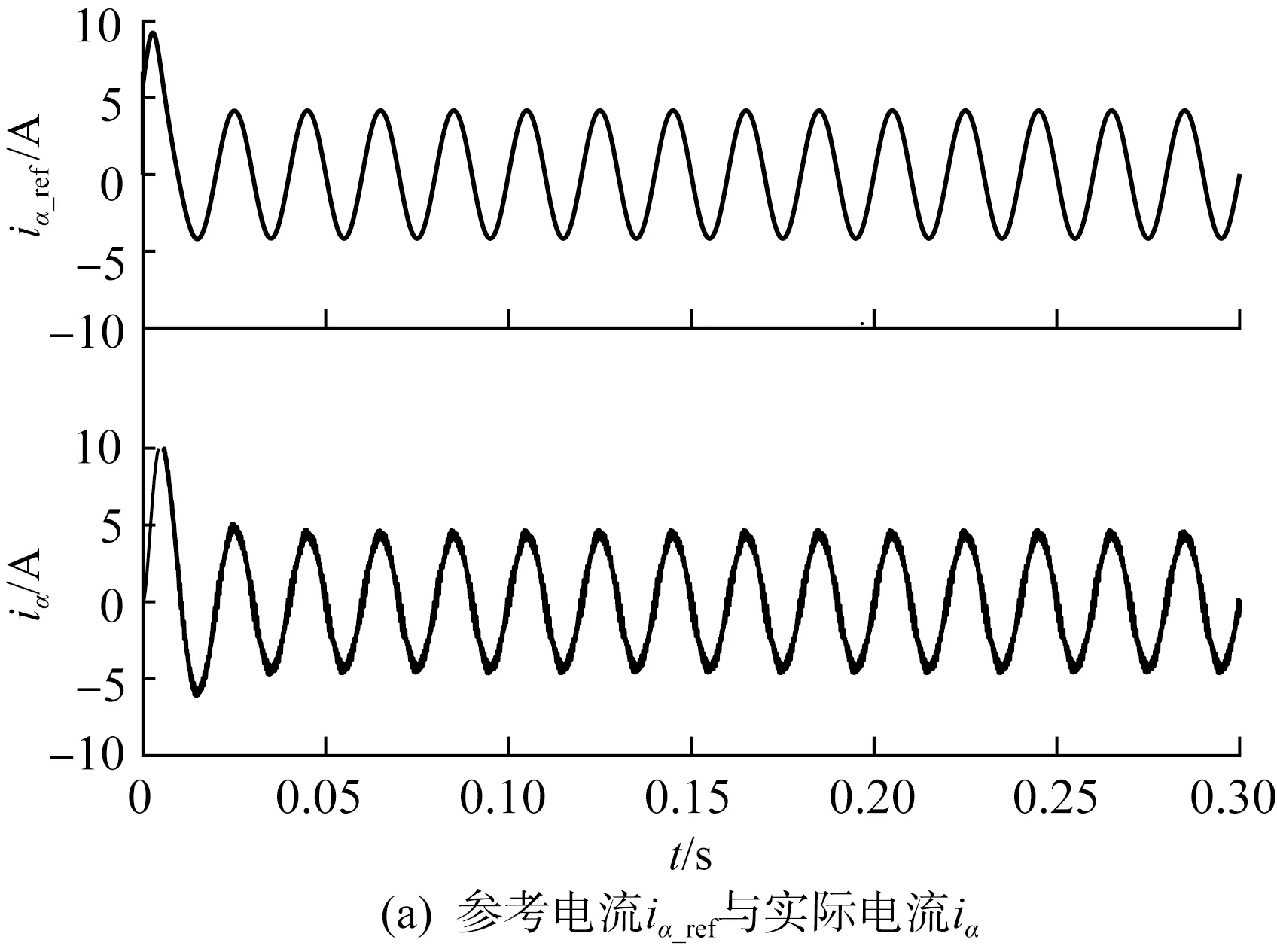
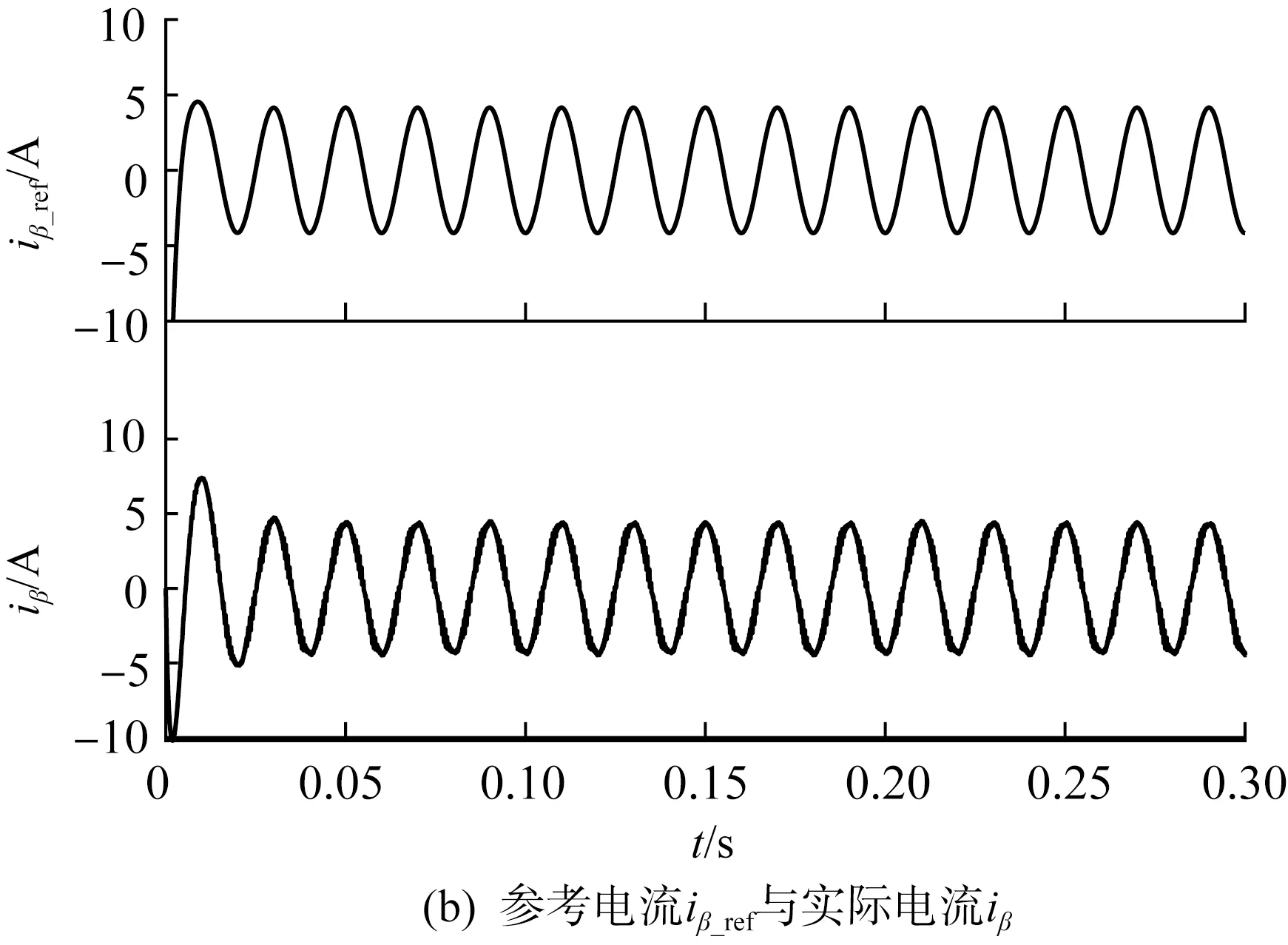
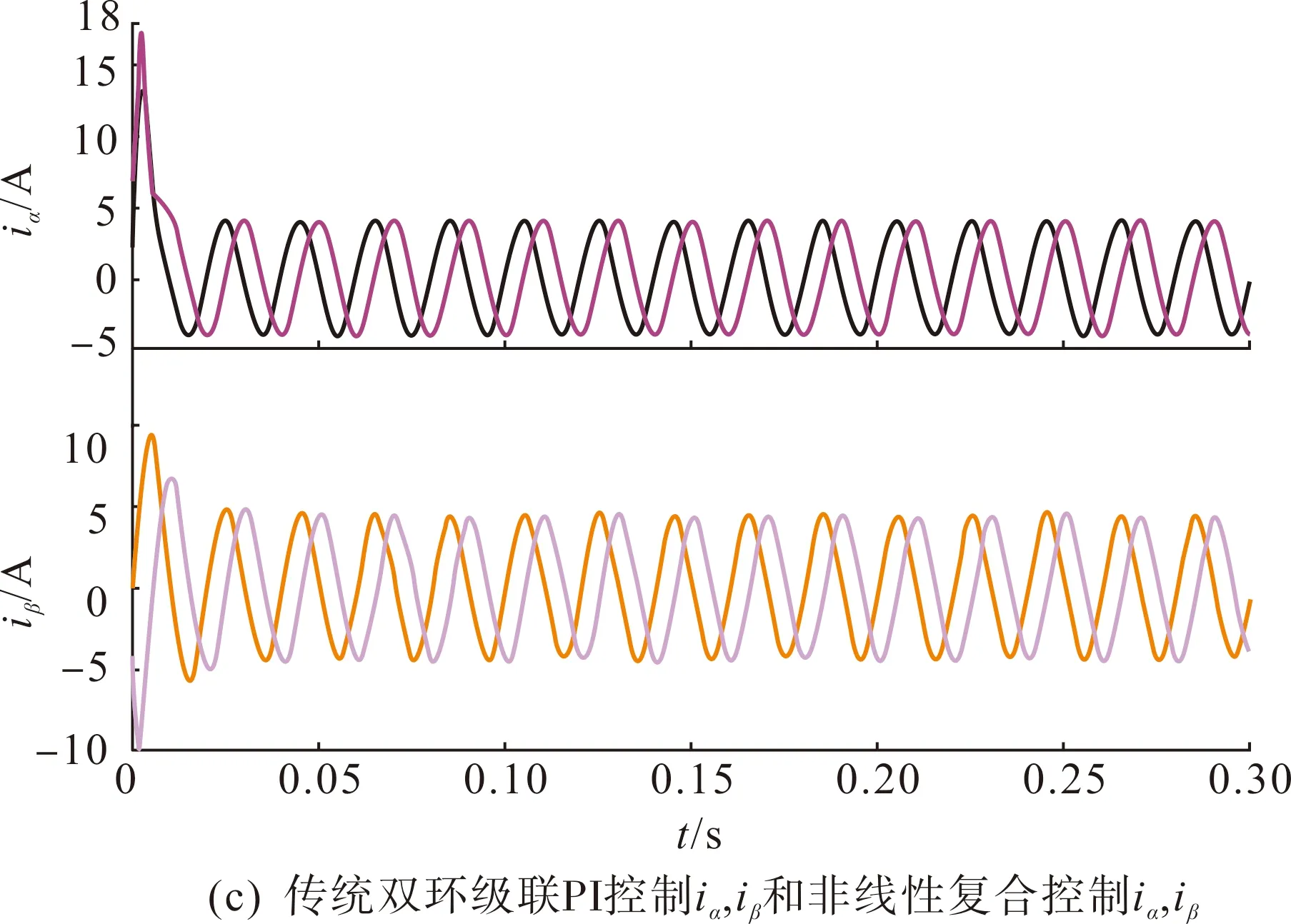
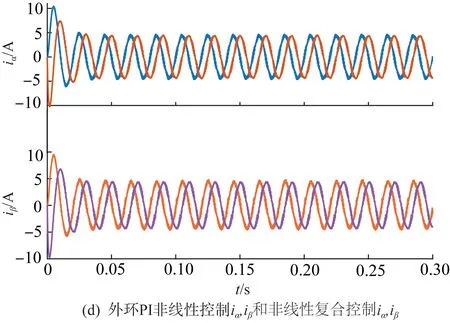
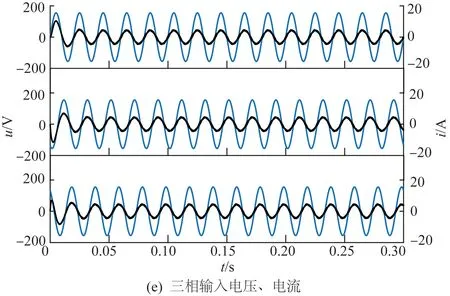
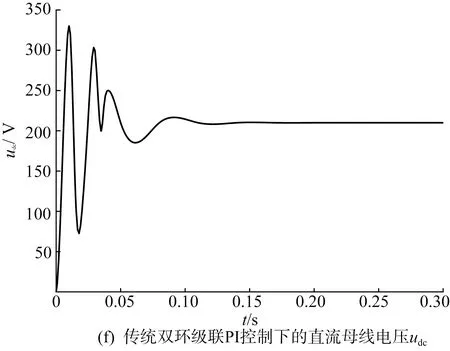
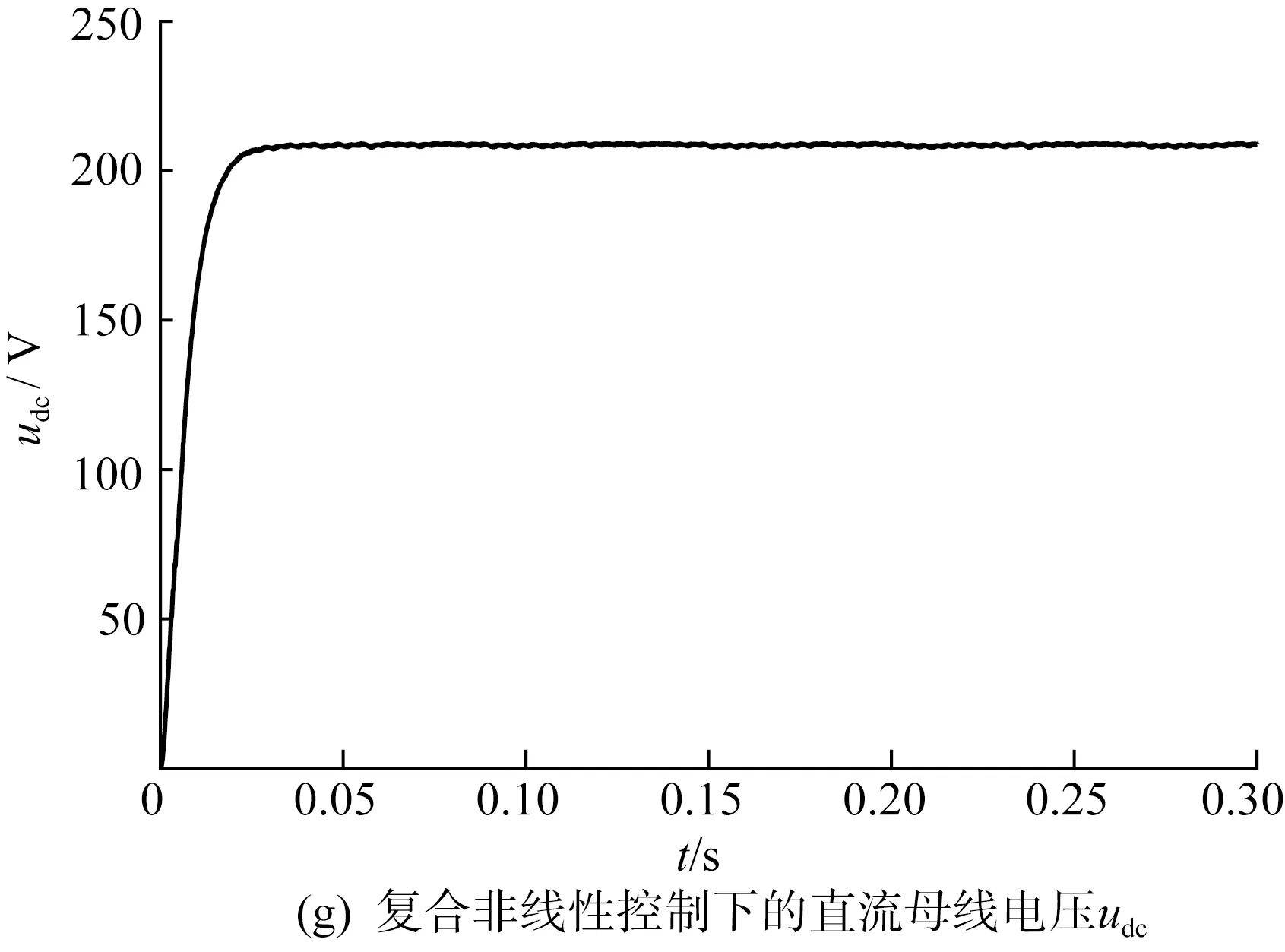
圖6 仿真結果Fig.6 Simulation results

通過對GSC的數學模型搭建以及仿真結果的驗證，證明了本文所提的控制策略在平衡電網下GSC控制具有優秀的動態性能。

8 結語

本文以DFIG網側變換器作為研究對象，提出了利用反饋線性化理論在兩相靜止坐標下對電流進行控制的方法，相比在同步坐標系下的控制方式，本控制策略無需電網電壓定向，減少了耦合項的引入，避免出現與傳統PI相同的復雜結構，實現了反饋線性化快速解耦；同時電壓外環采用含飽和函數的電壓滑模控制，提高了系統的動態性能。仿真結果表明，該控制方法具有很好的動態性能，并且實現了直流母線電壓的穩定以及網側功率因數控制，驗證了理論的正確性。上述控制策略也為不平衡電網下DFIG的GSC非線性控制提供了理論基礎。