考慮巡航速度調(diào)整的航班恢復(fù)優(yōu)化模型
崔麗娟,景崇毅,焦國慶,潘夏霖
(中國民用航空飛行學(xué)院機(jī)場工程與運(yùn)輸管理學(xué)院,廣漢618307)
0 引言
自二十一世紀(jì)以來,航空運(yùn)輸需求不斷增加,航空市場不斷擴(kuò)大,航空運(yùn)輸業(yè)正在蓬勃發(fā)展,同時航空公司的競爭也日趨激烈,航班編排越來越緊湊,導(dǎo)致不正常航班時有發(fā)生。航空公司如何合理地分配現(xiàn)有資源,從而低成本、高效率地進(jìn)行航班恢復(fù)對公司運(yùn)營效益和服務(wù)水平尤為重要。
不正常航班恢復(fù)問題是一個非常復(fù)雜的實(shí)時網(wǎng)絡(luò)優(yōu)化問題,其解空間隨著飛機(jī)和航班數(shù)量的增加而呈指數(shù)型增加,屬于NP-hard 問題,同時有實(shí)時優(yōu)化的需求[1]。關(guān)于航班恢復(fù)的文獻(xiàn)已經(jīng)頗為豐富,Teodorovic和Guberinic[2]考慮航班延誤和飛機(jī)交換,以旅客總延誤時間最小化為目標(biāo)建立針對飛機(jī)故障的數(shù)學(xué)模型,對飛機(jī)路徑和航班時刻進(jìn)行了恢復(fù)。Jarrah 等人[3]針對飛機(jī)短缺問題根據(jù)航班延誤和航班取消兩種恢復(fù)策略分別建立了兩個航班恢復(fù)成本最小化的網(wǎng)絡(luò)流模型,但這兩個模型不能同時使用,所以在航班恢復(fù)過程中不能同時考慮航班延誤和航班取消。Argüello[4]為解決飛機(jī)短缺問題,在不考慮飛機(jī)交換的情況下以航空公司收益損失最小和旅客總延誤時間最短為目標(biāo)建立航班恢復(fù)模型,首次采用貪婪隨機(jī)自適應(yīng)搜索算法求解該模型。Aktürk 等人[5]首次將巡航速度調(diào)整明確引入航班恢復(fù)模型,為便于求解通過二次圓錐曲線對模型進(jìn)行重構(gòu)。周靖為[6]針對飛機(jī)故障時間的不確定性建立了航班時刻和飛機(jī)路徑恢復(fù)的數(shù)學(xué)模型,并根據(jù)模型的特點(diǎn),選用Benders 分解法求解該模型。趙秀麗[7]在經(jīng)典的資源指派模型的基礎(chǔ)上,完善了飛機(jī)路徑恢復(fù)約束條件,從旅客和航空公司的角度設(shè)置了不同的恢復(fù)目標(biāo)函數(shù),并分析了不同目標(biāo)函數(shù)對恢復(fù)方案的影響。白鳳[8]在時空網(wǎng)絡(luò)模型的基礎(chǔ)上提出了多商品流模型,并采用不同的算法分別對飛機(jī)路徑和機(jī)組進(jìn)行恢復(fù)。王峰[9]針對機(jī)場關(guān)閉帶來的航班中斷問題,分別建立了恢復(fù)時間確定和恢復(fù)時間不確定的兩種航班恢復(fù)模型,對飛機(jī)路徑進(jìn)行恢復(fù)。
通過分析現(xiàn)有研究成果可知,將巡航速度調(diào)整明確地納入到航班恢復(fù)模型的研究寥寥無幾。而在航空公司實(shí)際的運(yùn)營過程中,巡航速度調(diào)整在航班恢復(fù)中被普遍使用,因此,本文基于航班取消、航班延誤、飛機(jī)交換和巡航速度調(diào)整四種恢復(fù)策略,以航班恢復(fù)成本最小為目標(biāo)建立航班恢復(fù)模型,為航空公司及時、高效地應(yīng)對不正常航班提供理論參考。
1 問題描述與模型構(gòu)建
1.1 問題描述
航空公司在處理不正常航班計劃的過程中,常常會考慮航班延誤,航班取消,飛機(jī)交換三種恢復(fù)策略,飛機(jī)巡航速度的調(diào)整也是經(jīng)常被使用的一種恢復(fù)策略,巡航速度調(diào)整在航班恢復(fù)過程中具有重要的意義。
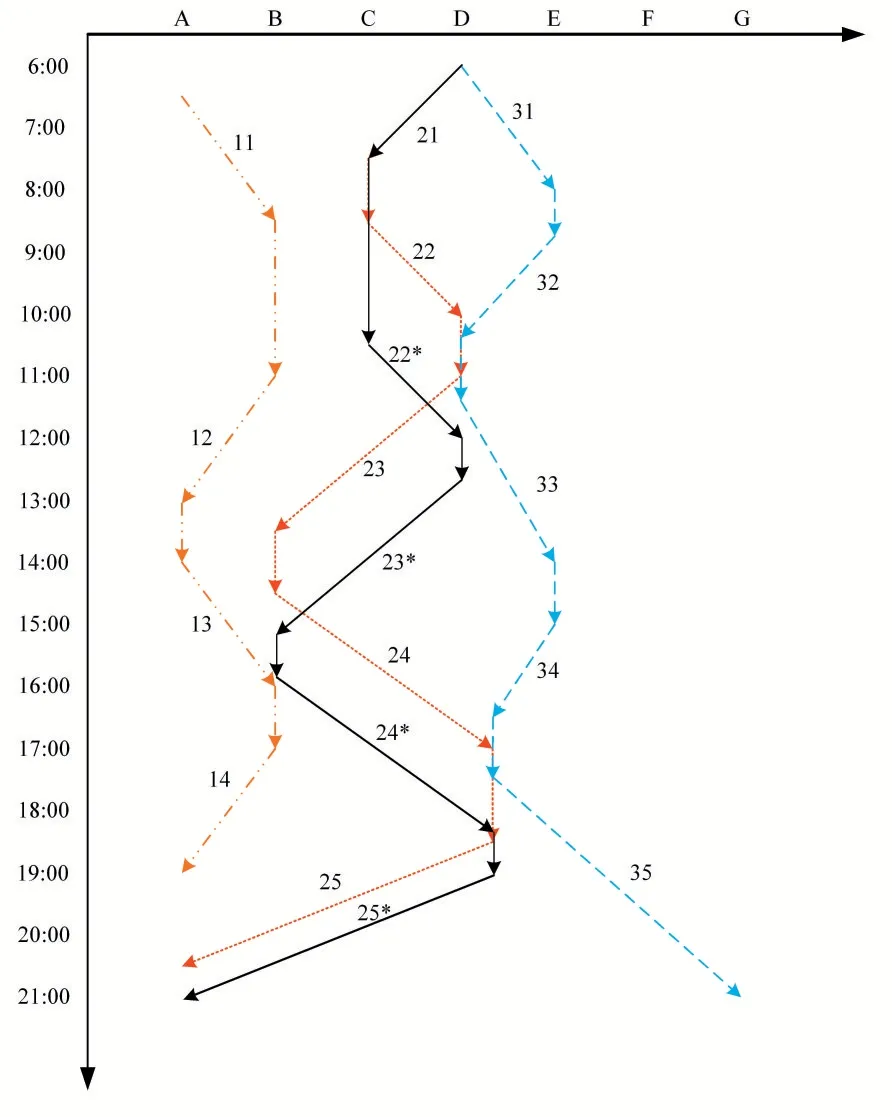
圖1 巡航速度調(diào)整對航班恢復(fù)的影響示意圖
在航班恢復(fù)過程中改變飛機(jī)的巡航速度主要有兩個作用:一是縮短巡航時間使航班可以盡早到達(dá)目的地,減少航班的到達(dá)延誤時間,從而減少航班的延誤成本。如圖1 所示,3 架飛機(jī)在7 個機(jī)場之間執(zhí)行14 個航班,例如航班11、航班12、航班13、航班14 是由飛機(jī)1 執(zhí)行的四個連續(xù)航班。由飛機(jī)2 執(zhí)行的航班22 出發(fā)延誤90 分鐘,紅色虛線表示飛機(jī)2 的原始航班計劃,黑色實(shí)線代表恢復(fù)之后的航班計劃示意。左圖是順延方案下的航班恢復(fù)方案,在航班22 的影響下航班23*、航班24*、航班25*三個后續(xù)航班都有不同程度的延誤;右圖是巡航速度調(diào)整之后的航班恢復(fù)方案,航班22*、航班23*、航班24*都進(jìn)行了加速,在航班25 出發(fā)之前航班延誤時間被抵消,航班25 可以按原航班計劃執(zhí)行。二是飛機(jī)增加巡航速度之后,可以進(jìn)行相應(yīng)的飛機(jī)交換,保證重要航班的正常執(zhí)行,減少航班恢復(fù)的總成本。如航班22*適當(dāng)?shù)丶铀僦螅艉桨?2 進(jìn)行適當(dāng)?shù)募铀伲桨?2*的飛機(jī)就可以與航班32 的飛機(jī)進(jìn)行飛機(jī)交換,從而保證后續(xù)航班的順利進(jìn)行。
增加巡航速度對降低航班恢復(fù)成本有利也有弊。一方面增加巡航速度可以減少航班的巡航時間,縮短航班延誤時間,從而減少航班延誤成本;另一方面隨著巡航速度的增加,飛機(jī)的燃油消耗也會增加,進(jìn)而帶來額外的燃油成本。所以利用巡航速度調(diào)整進(jìn)行航班恢復(fù)時,需要在延誤成本和額外燃油成本之間進(jìn)行權(quán)衡。
1.2 航班恢復(fù)模型的構(gòu)建
本節(jié)在考慮航班延誤、飛機(jī)交換、巡航速度調(diào)整三種恢復(fù)決策的基礎(chǔ)上建立單機(jī)型的航班恢復(fù)模型。
(1)集合
L:航班集合
Ld:原始受擾航班集合
S(l):可能進(jìn)行飛機(jī)交換的航班l(xiāng)的集合
(2)參數(shù)
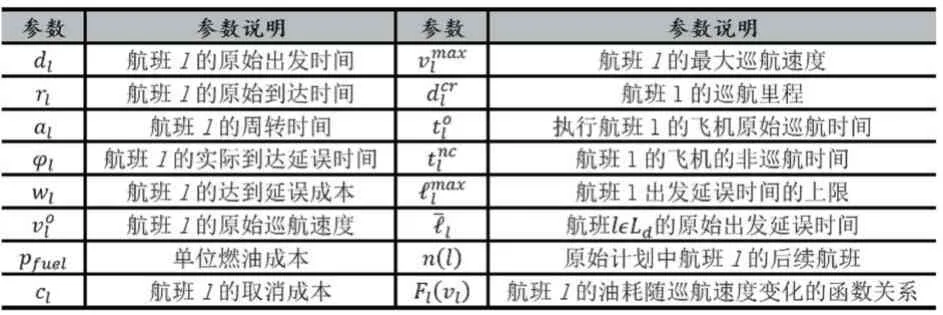
表1 模型參數(shù)及其說明
(3)決策變量
vl:航班l(xiāng) 的巡航速度
tl:航班l(xiāng) 的巡航時間
ll:航班l(xiāng) 的出發(fā)延誤時間
xlg:若航班l(xiāng) 和航班g 進(jìn)行飛機(jī)交換,則為1;否則為0。
yl:若航班l(xiāng) 取消,則為1;否則為0。
(4)目標(biāo)函數(shù)
巡航速度增加可以在一定程度上減少航班延誤時間,從而降低延誤成本,同時也會使油耗增加,從而到來額外的燃油成本。因此,目標(biāo)函數(shù)中除了航班取消成本和航班延誤成本之外,應(yīng)加入額外燃油成本。
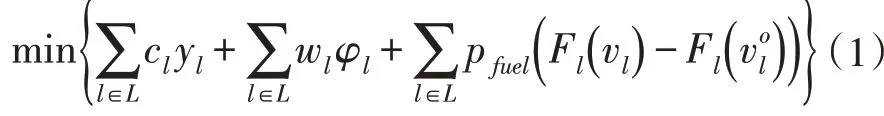
(5)約束條件
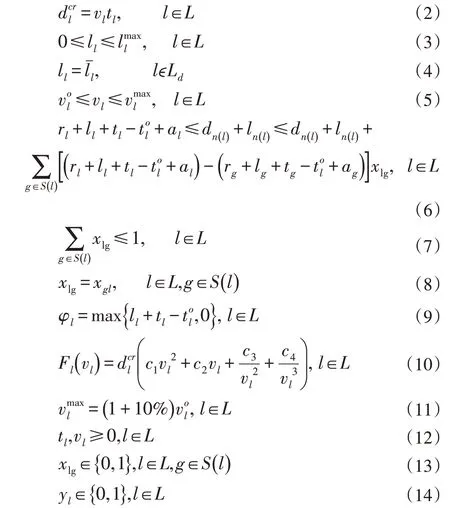
約束(2)表示航班巡航距離與巡航速度的關(guān)系,其中巡航距離可通過原始巡航速度與原始巡航時間的乘積求得,即。公式(3)表示航班出發(fā)延誤約束。恢復(fù)之后的航班出發(fā)時間不早于原始出發(fā)時間,并且不能晚于最晚延誤時間。公式(4)定義了航班出發(fā)延誤。航班的出發(fā)延誤等于原始中斷航班的原始出發(fā)延誤時間。公式(5)恢復(fù)之后的航班巡航速度約束。恢復(fù)之后的航班巡航速度不得小于原始航班巡航速度,并且不能大于該航班狀態(tài)下的最大巡航速度。公式(6)表示航班出發(fā)時間約束。當(dāng)航班l(xiāng) 與航班g 不進(jìn)行飛機(jī)交換時,航班l(xiāng) 的后續(xù)航班n(l)的出發(fā)時間不得早于恢復(fù)之后航班l(xiāng) 的到達(dá)時間加上航班l(xiāng) 的地面周轉(zhuǎn)時間,即rl+ll+tl-tol+al≤dn(l)+ln(l);當(dāng)航班l(xiāng) 與航班g 進(jìn)行飛機(jī)交換時,航班l(xiāng) 的后續(xù)航班n(l)的出發(fā)時間不得早于恢復(fù)之后航班g 的到達(dá)時間加上航班g 的地面周轉(zhuǎn)時間,即rg+lg+tg-tog+al≤dn(l)+ln(l)。公式(7)和(8)是對航班交換飛機(jī)的頻次約束。保證每兩個航班之間最多只能交換一次飛機(jī),并且進(jìn)行飛機(jī)交換的兩個航班要同時換飛機(jī)。公式(9)表示恢復(fù)之后航班到達(dá)延誤時間。公式(10)是航班燃油消耗的公式,該公式引自參考文獻(xiàn)[5]。公式(11)保證恢復(fù)之后的航班巡航速度不得超過初始航班速度的110%。本研究假設(shè)航班的初始巡航速度為最大航程(MRC)速度的102%。公式(12)(13)(14)是對決策變量取值的約束。
2 算例測試
為驗證該模型的可行性及有效性,本節(jié)結(jié)合航空公司的實(shí)際運(yùn)營情況及合理的假設(shè),進(jìn)行數(shù)值檢驗及分析。航班信息截取于國內(nèi)某航空公司2020 年冬季航班中某天的航班計劃,5 架飛機(jī)在11 個機(jī)場之間執(zhí)行的20 個航班,具體航班信息見表2。
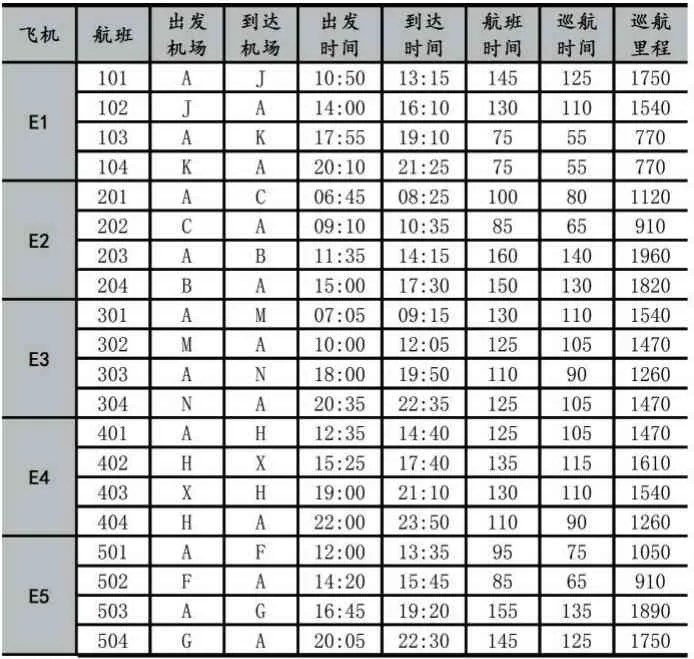
表2 航班信息表
假設(shè)航班延誤成本為120 元每分鐘;航班出發(fā)延誤時間超過180min 時,取消該航班;每個航班的最小地面周轉(zhuǎn)時間為30min、非巡航時間為20min。
當(dāng)飛機(jī)1 由于飛機(jī)故障需在A 機(jī)場需要停場4 小時(10:00-14:00),用手動順延方案、歷史方案(航班取消、航班延誤、飛機(jī)交換)和優(yōu)化方案(巡航速度調(diào)整、航班取消、航班延誤、飛機(jī)交換)分別進(jìn)行航班恢復(fù)。
手動順延方案:由于航班101 延誤時間超過180min,所以取消航班101 和航班102,航班103 和航班104 按原計劃執(zhí)行。取消航班的取消成本相當(dāng)于延誤180min 的成本,計算恢復(fù)效率時,取消航班的延誤時間取180min。
歷史方案:飛機(jī)1 和飛機(jī)4 進(jìn)行交換,航班101、航班102、航班103 和航班104 可按原計劃執(zhí)行;航班401、航班402 和航班403 分別延誤85min、70min、20min。
優(yōu)化方案:飛機(jī)1 和飛機(jī)4 進(jìn)行交換,航班101、航班102、航班103 和航班104 按原計劃執(zhí)行。航班401、航班402 進(jìn)行不同程度的加速后,在航班403 出發(fā)之前完全抵消了延誤,航班403 及其之后的航班按原計劃執(zhí)行,優(yōu)化方案的具體結(jié)果見表3。
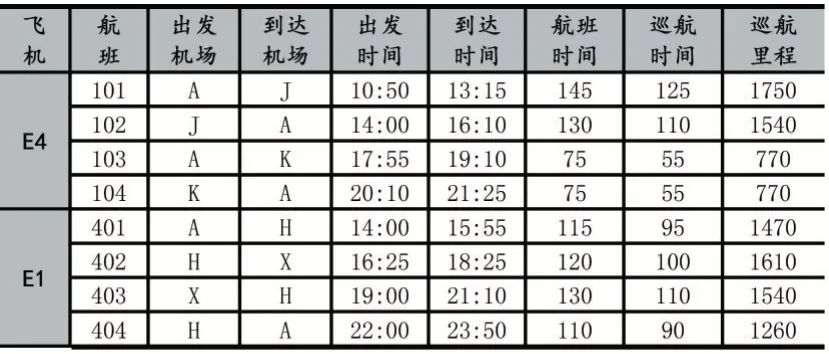
表3 優(yōu)化方案
表4 給出了三種方案恢復(fù)成本的比較。優(yōu)化方案和手動順延方案相比較,恢復(fù)成本較低65.40%,恢復(fù)效率提高51.39%;和歷史方案相比,恢復(fù)成本降低28.82%,恢復(fù)效率提高31.43%。
單位延誤成本分別取80 元每分鐘、120 元每分鐘、160 元每分鐘、200 元每分鐘時,優(yōu)化方案和歷史方案相比較,恢復(fù)成本分別降低27.51%、28.82%、29.47%、29.86%,因此單位航班延誤成本越高,巡航速度控制降低恢復(fù)成本的效果越明顯。
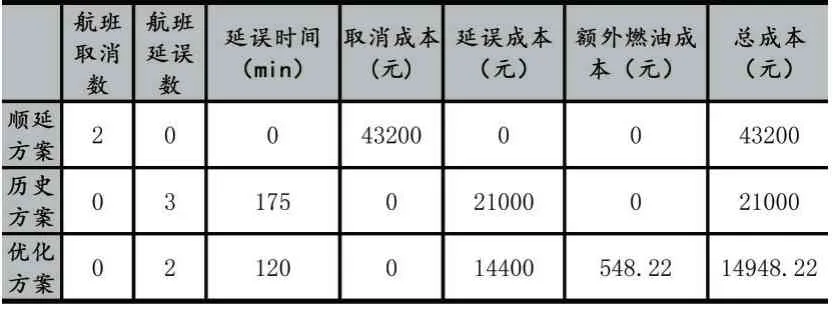
表4 三種方案結(jié)果比較
3 結(jié)語
本文針對發(fā)生飛機(jī)故障時航班計劃受擾的情況,采用巡航速度調(diào)整、飛機(jī)交換、航班延誤、航班取消四種恢復(fù)策略對航班進(jìn)行恢復(fù),并用MATLAB 軟件進(jìn)行求解。本文運(yùn)用算例對模型進(jìn)行過了測試,結(jié)果表明,該模型在降低航班恢復(fù)成本的同時,也提高了恢復(fù)效率;通過優(yōu)化方案和歷史方案的對比,可知,單位航班延誤成本和巡航速度調(diào)整對降低成本的效果成正比。
本文只對單機(jī)型進(jìn)行了建模,若對不同機(jī)型執(zhí)行的航班進(jìn)行恢復(fù),需要對模型進(jìn)行延展;航班恢復(fù)包括飛機(jī)恢復(fù)、時刻恢復(fù)、機(jī)組恢復(fù)和旅客恢復(fù),但該模型沒考慮機(jī)組恢復(fù)和旅客恢復(fù)。

