基于序列關聯的參差信號分選算法

王俊嶺 黃琰璟

(北京理工大學信息與電子學院 北京 100081)

1 引言

雷達信號分選一直是雷達通信與電子戰主要研究的重點問題之一，目的是將接收到的脈沖串分離開，得到環境中的雷達輻射源信息。信號分選主要包括基于脈沖調制參數脈寬(Pulse Width, PW)、脈沖到達角(Direction Of Arrival, DOA)、射頻頻率(Radio Frequency, RF)以及時域波形或頻譜[1-4]等脈內參數的預分選和基于脈沖串的各個脈沖到達時間(Time Of Arrive, TOA)的主分選。

主分選算法的主要目的是通過對脈沖對間隔的處理以得到待處理脈沖串中的各個輻射源的脈沖重復間隔(Pulse Repetition Interval, PRI)與PRI的調制形式。對脈沖對間隔的處理方法中，有許多經典算法如累計差值直方圖算法[5](Cumulative DIFferences Histogram, CDIF)和以CDIF為基礎的序列差值直方圖算法[6](Sequential DIFferences Histogram, SDIF)。相比CDIF方法，SDIF實現簡單，提高了PRI分選效率，在工程上有大量的應用，但是SDIF直方圖中過門限的峰值僅為可能的PRI值，需額外進行諧波檢查，在電磁環境復雜時，諧波檢查會增加虛警率。Nishiguchi等人[7]為解決上述兩種算法存在的諧波抑制方面的不足，基于時延自相關的原理，為直方圖中加入了相位因子，提出了PRI變換算法。文獻[8-10]通過改進PRI變換算法中相位因子和PRI箱的結構，提高了對抖動信號和部分脈沖丟失信號的分選能力。但是由于PRI算法及其改進算法在PRI變換中加入了相位因子，導致在分選參差信號時，參差信號的幀周期被抑制，以至于難以被分選。文獻[11-13]針對參差信號幀周期的分選問題，對PRI變換算法和序列抽取算法進行了結合，減少環境復雜度，能在提取參差序列后對環境進行PRI判斷。根據現有算法的原理可知，現有算法大都致力于找到一個脈沖串的特征，從而忽略了單個脈沖之間的關聯，本文通過建立脈沖對間隔( ΔT)與單個脈沖的聯系，在擴展關聯法和特征向量法[14-16]的基礎上，給出了一種脈沖間隔分布矩陣的建立方法。通過對該矩陣的處理，可在抑制諧波和參差幀周期提取的同時，提取出輻射源對應的脈沖串，鑒別PRI調制特征以及提取參差信號子序列。由于計算次數為脈沖對的個數，該方法的計算復雜度與PRI變換算法保持一致。

本文的結構如下，在第2節對信號分選及參差信號模型進行介紹，對PRI變換和直方圖算法的固有缺陷進行分析。在第3節介紹脈沖間隔分布矩陣的建立方式和性質，整體算法流程、門限確定和算法檢測性能分析。第4節給出算法的仿真結果。第5 節是對全文的總結。

2 信號分選模型及PRI變換算法

本節主要介紹基于脈沖串TOA分選的信號主分選模型，并分析基于PRI變換的方法在參差信號分 選中的局限性。

2.1 信號主分選及參差信號模型

對于一個由N個脈沖構成的脈沖串，在只考慮脈沖TOA時，可以定義為如式(1)的形式

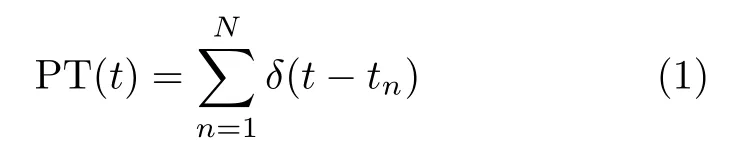
其中，tn為 第n個脈沖的TOA, δ (t)為沖激響應函數。

信號分選的目的是分選脈沖串里的具有一定相關性的脈沖，獲得脈沖串中的雷達PRI調制參數。

對參差信號，其PRI可以看作多個固定PRI脈沖序列的疊加，參差信號的幀周期定義為

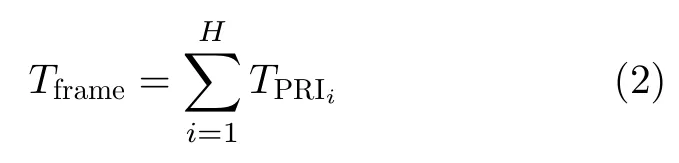
每一個幀周期為一個參差子序列循環，其示意圖如圖1所示。

2.2 基于Δ T直方圖的信號分選算法

ΔT 直方圖算法是一種提取輻射源PRI統計特性的有效方法。CDIF算法為典型的基于Δ T直方圖的方法，其中的累積差值是指：算法先計算兩個相鄰脈沖之間的差值，即1階直方圖，并對結果進行門限檢測。之后對相隔1個脈沖的脈沖對進行統計，稱為2階直方圖，并累積到原1階直方圖上，再次進行門限檢查。SDIF是對CDIF的優化算法，在計算1階以上的直方圖時，不與1階直方圖合并，而是產生1個獨立的直方圖，并對所有直方圖進行獨立分析。然而，上述兩種算法本質上均是基于信號序列的自相關函數進行分析，存在序列諧波干擾。對此，研究人員提出通過PRI變換算法，加入相位因子的方式來抑制諧波[7]

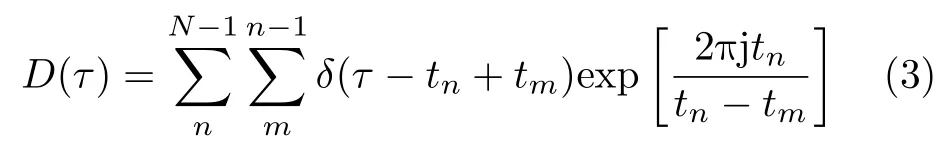
其中，tn,tm為第n和第m個脈沖的脈沖到達時間，相位因子為 e xp[2πjtn/(tn-tm)]。對于一個固定重復頻率的脈沖串，脈沖到達時間可表示為

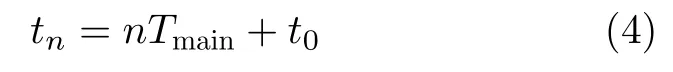
將式(4)代入式(3)，則有

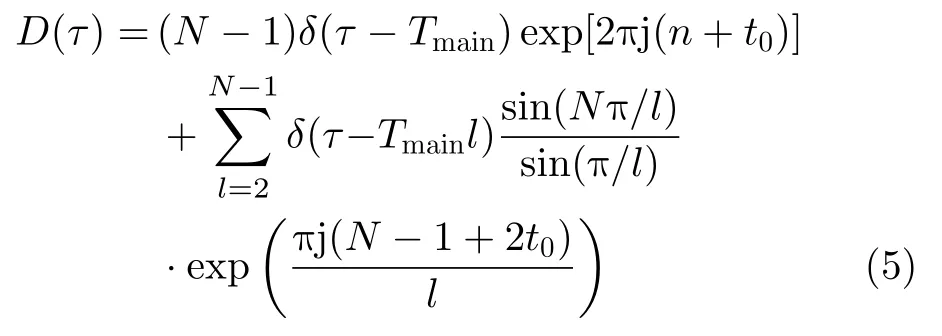
而對于不加入相位因子的PRI變換式為

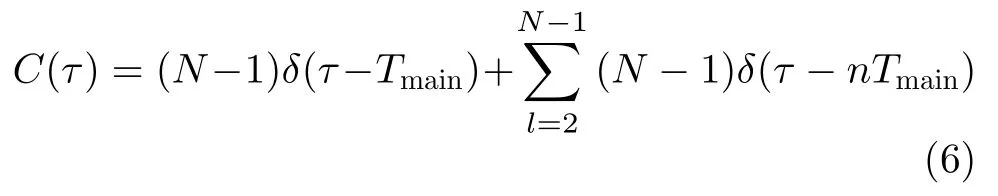
圖1 參差PRI脈沖序列

此外，PRI變換算法中還引入了PRI箱的概念，是指Δ T直方圖PRI的量化點，參數包括PRI箱的中心和范圍。之后的改進算法對PRI箱的設置方式進行了優化，增加了對抖動信號的檢測能力。

同理，對于參差PRI信號，其PRI變換可由式(2)代入式(3)得到

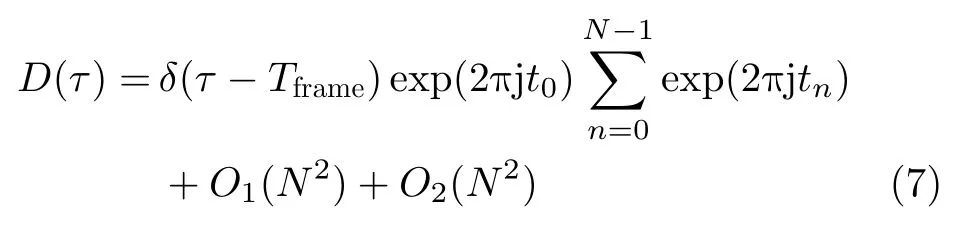
其中，式中第1項為參差幀周期的幅度表達式，O1(N2) 是諧波余項，O2(N2) 是mod(n-m,H)/=0的余項，因為這些余項都不落在參差信號的幀周期內，所以可以不考慮。

對比式(5)的周期和式(7)幀周期的幅度項可知，對于固定重頻信號的主值周期幅度

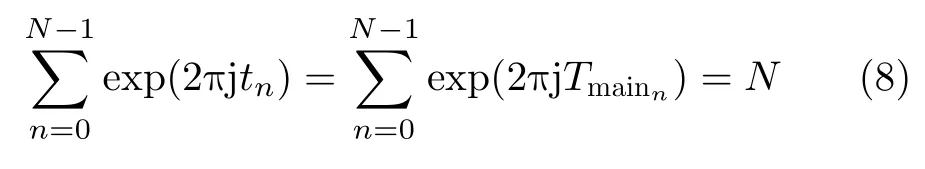
對于參差信號

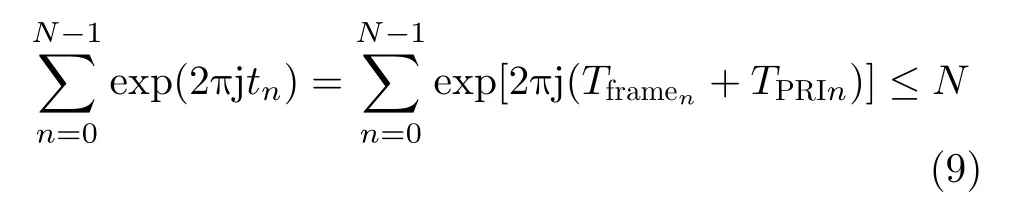
式(9)中，當且僅當TPRIn全 部為0或幀周期的整數倍時，取等號。而對于一般的情況，參差信號的子序列在單位圓上分布得越均勻，該幅度值越小。當序列PRI變化過大時，每一個PRI箱均無法累積到高于檢測門的幅度值。而對參差子序列相差很大的參差信號，不同的子序列會落在不同PRI箱內，導致參差子序列信號因單個PRI箱的累積幅度值不夠而不能被檢出。另外，相位因子對參差信號的幀周期有抑制作用，且抑制效果和諧波抑制效果相同，參差信號幀周期的幅度和諧波受到的抑制效果類似，若在這種情況下參差信號的幅度超過了門限函數，則諧波信號也會被檢出，相位因子的諧波抑制作用就失去了意義。

由于無法直接通過PRI變換算法的結果來獲取輻射源的調制信息，所以需要進行脈沖串序列提取。序列提取的傳統解決辦法是先選定頭脈沖，然后根據提取出的PRI幀周期序列之間的關系來確定整體脈沖序列。然而，對于參差PRI信號，通過單一頭脈沖只能提取參差信號部分脈沖，而且在參差子序列周期未知的情況下，很難提取參差輻射源整體脈沖。這 使得傳統方法的脈沖序列提取方法變得極為復雜。

3 一種基于PIDM的PRI分選方法

為解決PRI變換算法存在的參差信號幀周期抑制和序列提取困難的問題，考慮使用脈沖間隔分布矩陣(Pulse Interval Distribution Matrix, PIDM)來 克服上述缺點。

3.1 PIDM計算與PRI分選方法

PIDM是一個N×K的矩陣，矩陣中(k,n)元素的表達式為

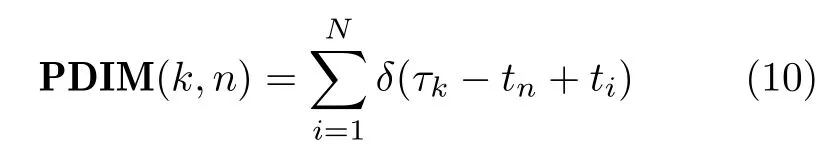
其中，N為一個分選幀的脈沖數，k為PRI箱的編號，n為脈沖編號。則(k,n)元素為第n個脈沖與其它脈沖的時間間隔為τk的次數統計值。

將式(4)定義的單一的固定重頻脈沖串，代入式(10)可得

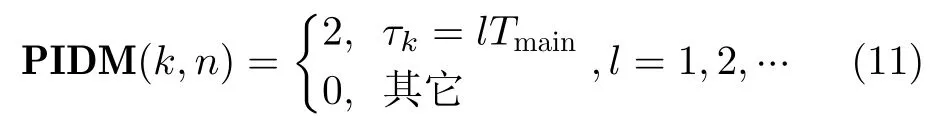
式(11)忽略了在脈沖串的邊界處幅度值為1的元素。

圖2(a)給出了固定重頻脈沖串按式(10)的計算結果，其中白色幅度值為2，黑色代表幅度值為0。由式(11)可知，當l=1時，τk=Tmain，為該脈沖串的PRI值，而 τk=lTmain(l ≥2)處存在諧波PRI值，需進一步進行諧波抑制處理。

根據2.2節對直方圖階數的介紹，可知高階直方圖為比低階直方圖更遠的兩個脈沖的時間差，所以諧波總是出現在高階直方圖中。在計算低階直方圖中的脈沖間隔時，當(k,n)處的幅度值被累加到2時，給第n個脈沖增加抑制標記，不參與更高階直方圖的計算，該處理方式可以抑制簡單環境下的諧波。不過，當環境存在干擾脈沖時，將會提前使某個脈沖在更小的PRI值處幅度值到達2，則會使得真實PRI處即更高階直方圖的時間間隔時的該脈沖被抑制。具體處理時可使用抑制諧波矩陣 M和不抑制諧波的矩陣 Mt， 當計算Mt的低階直方圖的時間間隔時，若幅度值超過了2，說明存在干擾脈沖，則取消該脈沖的抑制標記，使之可以繼續參與高階直方圖的時間間隔的計算。由此所得結果如圖2(b)所示，可以看到高次諧波已被抑制。對于參差信號(PRI為[0.9, 1.7, 1.9]，單位已歸一化)，采用上述方法計算PIDM并進行諧波抑制后，所得結果如圖2(c)所示(其中，灰色的點幅度值為1)。由于該諧波抑制算法只使用了統計的方法，可避免參差信號的幀周期被錯誤抑制的問題。

對于圖2(c)，為提取脈沖串的主周期，算法統計矩陣 M每一行的幅度值為2(以下稱為主周期行)的個數。圖3(a)給出了圖2(c)在PRI箱的對應統計結果，可以看到該脈沖串過門限的周期為4.5，與設置PRI參數一致。

為獲取脈沖串的調制形式，將 Mt( 而不是 M，可以保證提取的脈沖大于本應存在的脈沖數)矩陣中的τk=4.5行中幅度值大于2的所有脈沖提取出來，易知，這些脈沖為構成周期為4.5的所有脈沖和干擾脈沖。然后，將 Mt中未被提取出的脈沖的列置零后，再次統計每一行幅度值大于1的元素(以下稱為子序列行)的個數，計算直方圖結果如圖3(b)所示。由參差子序列的排列方式可知，統計出的子序列行由參差子序列的值和相鄰子序列相加產生。由圖3(b)可知，參差信號會在比幀周期小的位置出現峰值，對這些峰值進行門限檢測便可提取出參差信號的子序列。而對固定重頻脈沖序列，比主周期行直方圖中提取出的周期小的PRI箱中不會出現過門限峰值。由此可獲得主周期行直方圖中提取出周期的PRI調制形式。

綜上所述，可以分選參差信號的幀周期和具體的 子序列，克服了PRI變換的兩個缺陷。

3.2 算法流程

算法整體分為3個部分，算法框圖如圖4所示，可分為以下3個關鍵步驟：

(1) 諧波抑制：計算PIDM，并由此進行主周期分選；

(2) 序列提取與門限檢測：計算檢測門限，并根據檢測門限提取脈沖序列與子序列；

(3) 參差子序列檢測：輻射源調制方式判斷與參數提取。

具體步驟如下：

(1) 諧波抑制

本部分對應圖4的步驟(1)部分，主循環和抑制諧波具體算法流程如下：

(a) 初始參數，脈沖抑制標志Flag(N)，輸入參數為 M和Mt；

(b) 計算Δ t=tn-tm， 找到Δ t ∈τk；

(c) 計算Mt, Mt(k,m)=Mt(k,m)+1,Mt(k,n)=Mt(k,n)+1；

(d) 若Flag(m)=0且Flag(n)=0，則M(k,m)=M(k,m)+1 , M (k,n)=M(k,n)+1；

(e) 若 M(k,m)=2 且k ＞PRImin，則 該 脈 沖n的標志位Flag(m)=1；同理， M(k,n)=2且k ＞PRImin, Flag (n)=1；

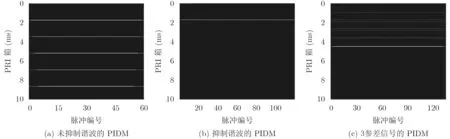
圖2 不同信號環境下的PIDM

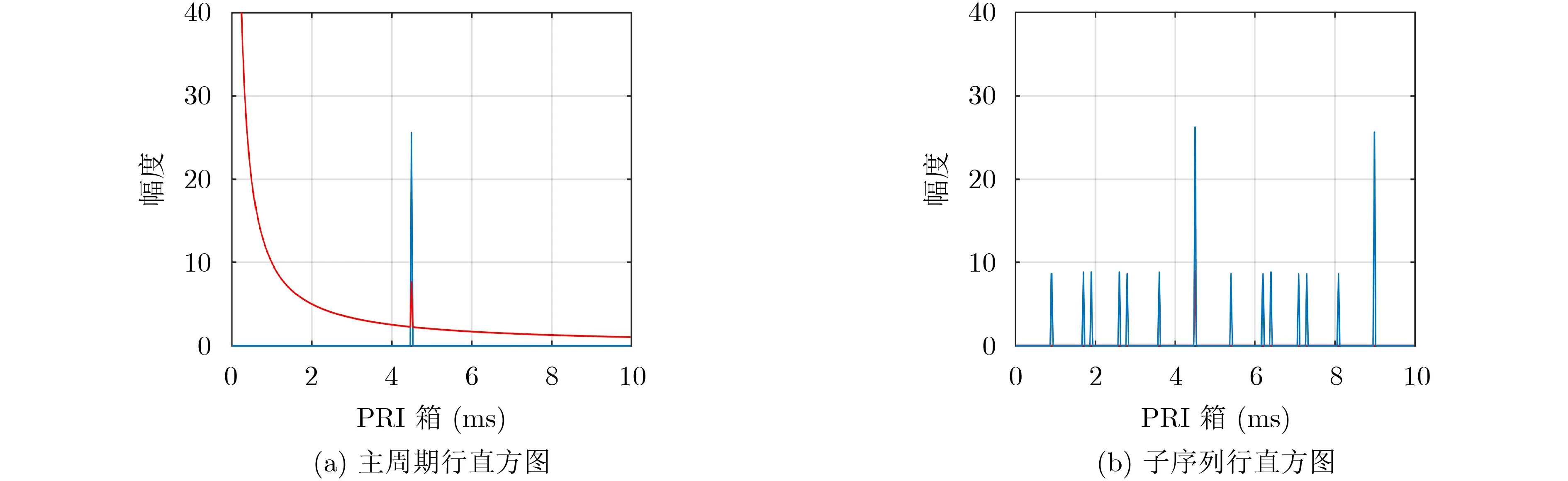
圖3 參差序列直方圖

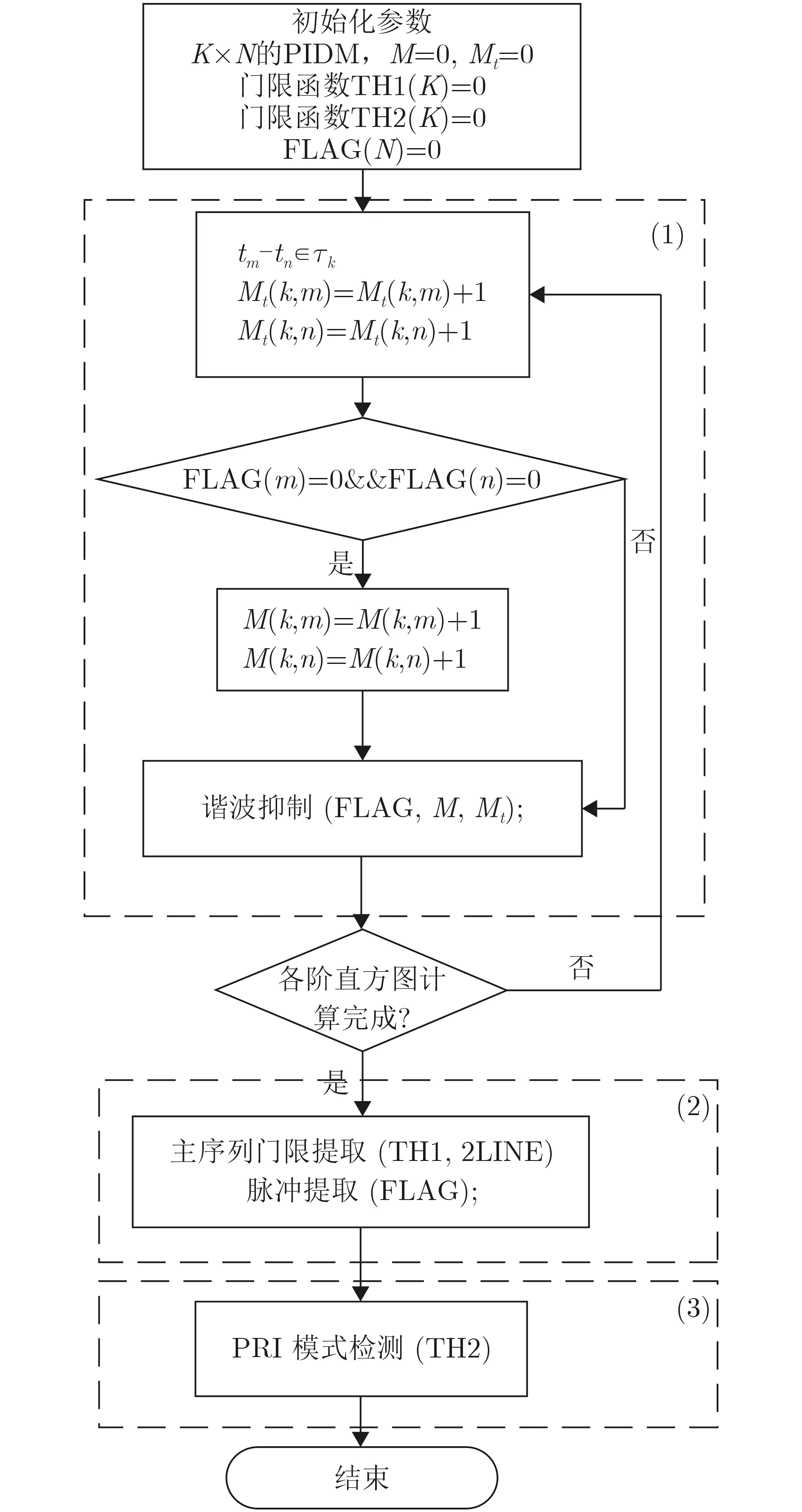
圖4 算法整體框圖

(f) 若 Mt(k,m)或 Mt(k,n)＞2，則兩個脈沖的標記Flag(n)=0, Flag(m)=0。

(2) 序列提取與門限檢測

本部分對應圖4的(2)部分，序列提取是根據主周期行直方圖提取出的周期找到對應于該周期的脈沖。在脈沖間隔循環計算后，此時進行門限檢測和序列提取。具體流程為：

(a)計算 M 矩陣中每個PRI箱的值＞2的脈沖數。

(b)對(2)(a)的結果進行主周期行門限檢測，得到所有過門限的PRI值。

(c)對矩陣 Mt=1的脈沖對應的PRI值進行序列提取，認為這些脈沖周期值為(2)(b)檢測出脈沖的周期值。

(d)對(2)(c)的結果進行子序列行門限檢測，參差序列檢測后得到分選結果。

直方圖的門限檢測函數是獲取子序列行直方圖和主周期行直方圖的前提。在PRI變換算法中，使用了3個門限，分別是噪聲門限、諧波門限以及脈沖密度門限。根據PRI算法門限設置原理，可相應設計主周期行直方圖門限值。具體設置方法如下。

主周期行直方圖門限設置：本文所提算法中，計算主周期行直方圖的目的是分選出脈沖流中的信號主周期。在主周期行處理中脈沖密度門限和PRI變換相同，由于諧波抑制方式的不同，計算諧波門限通過 Mt計算。而噪聲門限與PRI變換中的稍有不同。

因此，主周期行門限設置如式(12)所示

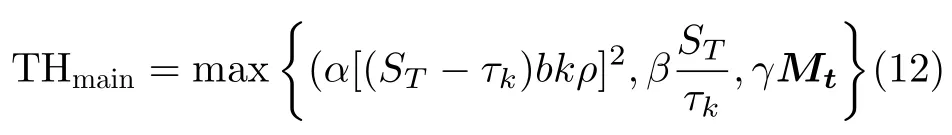
其中，函數m ax{·}表示求集合內最大值，第1項為噪聲門限，第2項為脈沖密度門限，第3項為諧波門限。 bk(PRI箱的寬度)和ST(脈沖串總時長)均為常數 τk為PRI箱的中心，ρ 為脈沖密度，α ,β和γ均為常量，根據仿真測試，分別設置為1.00, 0.42和0.07。

子序列行直方圖門限設置：根據前文分析，子序列行直方圖中的脈沖為構成輻射源脈沖串的脈沖加干擾脈沖，門限函數需要包括噪聲門限。此外，由于干擾脈沖是其它輻射源的脈沖，會在子序列行直方圖中增加其他輻射源主周期的干擾，所以門限函數還需加入諧波門限。

子序列行直方圖和主周期行直方圖的區別在于干擾脈沖數的不同，干擾脈沖對的數目來源于被提取的脈沖(C)和整體脈沖串(N)，噪聲脈沖對個數為N(N-C)。在一個脈沖固定位置的情況下，單個脈沖出現在任意一個PRI箱的概率為2 bk/T。由此可得噪聲均值和方差

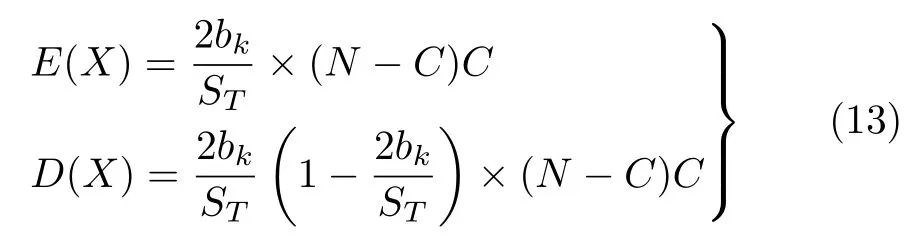
由于bk和 T 為固定值，經過序列提取后，E(X)與D (X)為常數。噪聲門限為

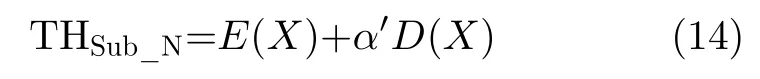
諧波門限與主周期行直方圖的諧波門限一致。根據式(12)和式(14)，可得子序列行直方圖的門限為

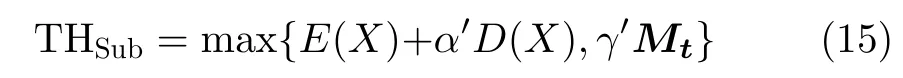
(3)參差子序列檢測

需要排除的周期一定是由真實的相鄰序列累加得到，因此可從序列的最小值開始檢索，找到互不能靠相加得到的子序列，這些子序列一定是所有子序列中的一部分。接著，刪除由這些被提取序列相加得到的序列。然后在對下一個未被刪除的子序列行值進行判斷，若與之前的序列相加剛好為幀周期，則輸出。否則在進行序列刪除操作后，繼續對下一個未被刪除的進行同樣的判斷，直到序列相加等于幀周期。通過這種方法，時間代價可降為O (H2lg H)。

3.3 算法性能分析

算法所需存儲空間為：K×N的矩陣2個用于存儲PIDM，1×N的矩陣輻射源個數用于脈沖諧波標記，1×K的矩陣輻射源個數用于存儲主周期行直方 圖。

4 仿真結果

為驗證本文提出方法的有效性，表1對比了在不同信號環境下采用常規PRI變換[7]和變換時間點的改進PRI變換[8]與本文算法的對比分析結果。采用本文提出的方法可以解決參差信號的幀周期提取問題以及實現參差子序列的提取。

圖5為文獻[7]和文獻[8]中的PRI分選算法所得結果，可以看到，兩個固定重頻的信號能夠過門限，而對于參差信號，由于相位因子對參差幀周期的抑制作用，檢測能力有限。

圖5(c)給出了采用本文算法所得的主周期行直方圖，部分序列提取的結果則如圖6所示，由圖6可知，本文所用算法可以同時檢測固定重復頻率信號和參差信號。具體的分析過程如下：

由于圖6(a)的主周期內沒有過門限的PRI箱值，可知圖6(a)為固定重復頻率信號。對于圖6(b)，過門限的PRI值有6個，分別為：{0.90, 1.65,1.95, 2.55, 2.85, 3.60}，根據對子序列行可能出現的數目分析，可得到參差信號數為3個。根據參差序列提取算法，0.90, 1.65, 1.95不能靠其他可能的子序列相加得到，為子序列的一部分，而2.55,2.85, 3.60可由0.90, 0.165, 1.95相加得到。可推知2.55, 2.85, 3.60應為被排除的PRI值，并且由0.90+1.65+1.95=4.50，所以，該序列為幀周期為4.5，子序列為0.90, 1.65, 1.95的3參差序列。

表1 不同信號環境下對比結果

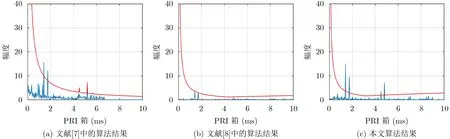
圖5 對比算法處理結果

為驗證算法在復雜場景下的穩定性，在包含參差信號的5種不同信號組合模式的隨機信號環境下進行了1000次蒙特卡羅仿真實驗，在每次蒙特卡羅仿真實驗中，每個組合模式中參差信號參數及固定重復頻率信號參數均隨機生成。表2給出了在3種不同指標要求下，本文提出算法與參照算法的分選成功概率對比情況。其中，3種指標要求分別為：能正確分選目標信號并且無任何重頻提取錯誤Presolv、在允許存在若干錯誤重頻的基礎上能夠全部分選出目標信號Pdistc、能分選出目標信號并且參差子序列的計算結果正確PdistcSTG。此外，由于文獻[7]和文獻[8]中的算法無參差信號檢測功能，所以當輻射源設置中有固定重頻信號時，若算法能夠分選出所有固定重頻的信號就會標記為該方法分選成功。

由表2可見，對不同參差重頻信號和固定重頻混合場景，本文算法均能有效地分選出參差信號，且在環境中輻射源增加時，本方法相比傳統方法仍能夠保持較高的分選概率。同樣由表2可知，在信號環境中的輻射源個數增加時，所提出方法和參照算法的性能均存在一定下降，但本文算法受輻射源間脈沖干擾的影響相對較小， Pdistc仍能保持在90%以上，參差子序列的高提取概率也驗證了本文算法在子序列提取方面的有效性。必須指出的是，在計算表2的分選概率時，本文算法所統計的是所有信號分選均無錯誤的分選概率，而其他算法則不考慮參差信號是否能正確分選，而只考慮了信號環境中固定重復頻率信號的分選概率，因此表2中本文算法所得分選概率的實際指標要求相對更為嚴格。

為驗證3個算法在相同信號環境和指標要求下的信號分選性能，在脈沖丟失概率為5%的場景下，圖7給出了1000次蒙特卡羅仿真對比驗證試驗的試驗結果。由圖7(a)和圖7(b)可知，隨著輻射源個數的增加，所有算法的檢測概率均有一定降低。不過，由于本文算法是基于脈沖對的關聯方法，脈沖丟失對算法結果影響較小，因此本文算法在輻射源遞增時仍能保持較高的固定重復頻率信號檢測概率，相比要優于參照算法。

綜上所述，仿真結果表明，本文算法在有參差信號存在的情況下相對傳統算法具有更好的檢測性能與穩定性，同時還具備檢測參差信號具體子序列的 優勢。

5 結束語

本文針對復雜環境下的PRI分選問題，提出了一種基于PIDM的直方圖算法。該方法不僅可避免在參差信號存在時傳統PRI分選方法抑制參差信號幀周期的缺陷，而且通過脈沖序列信息的利用，還可提取參差信號子序列，解決了傳統算法難以檢測信號參數的問題。分析表明，仿真結果驗證了本文算法的有效性和穩定性。

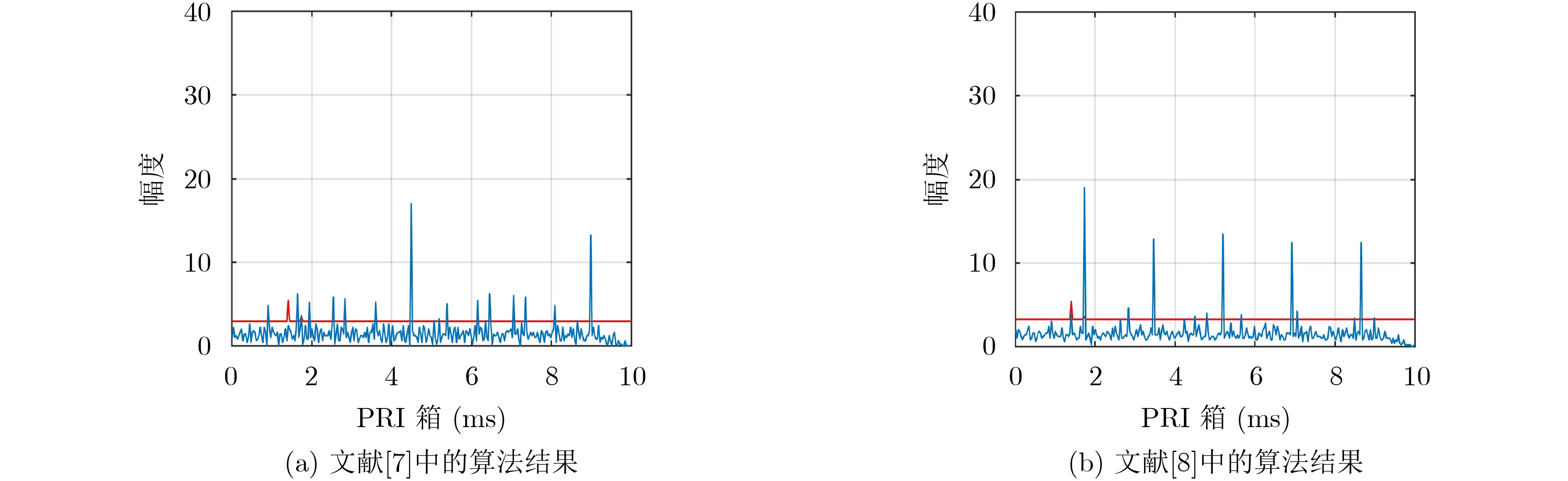
圖6 被分選出的部分輻射源的子序列行直方圖

表2 在隨機信號環境中本文算法/文獻[7]/文獻[8]分選成功概率(%)

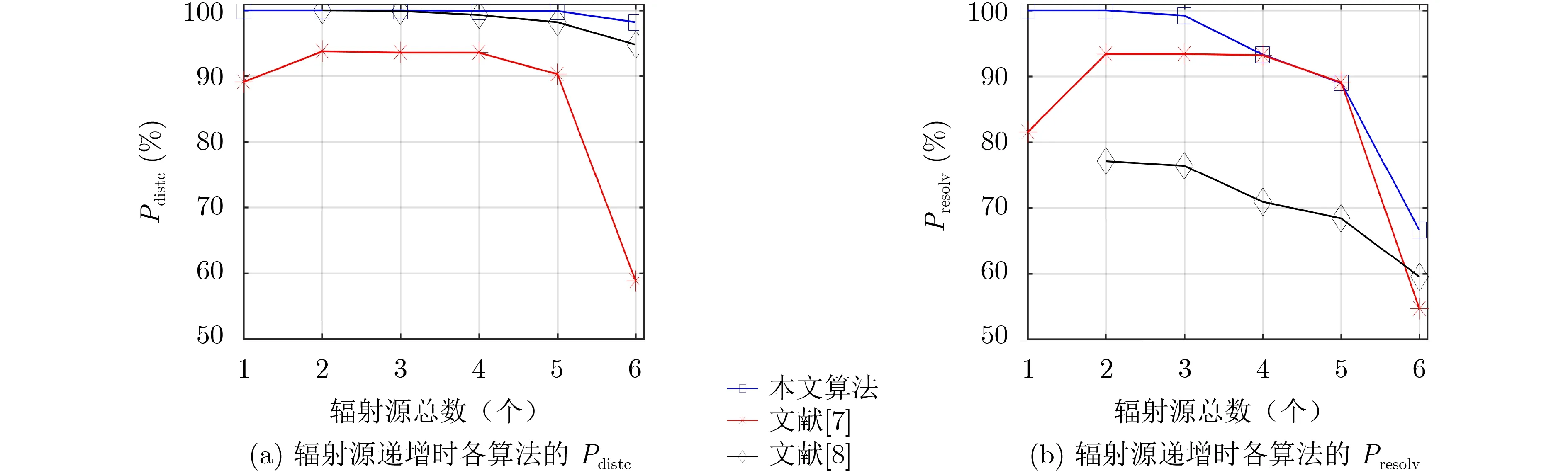
圖7 不同輻射源個數下固定重頻信號檢測概率