基于Matlab的加權隨機點名提問系統設計

黃秋豪 任呈祥 王旭 陳飛 錢祥利

摘要：該文從教學需求出發，設計一套具有權重的隨機點名課堂提問系統，其目的是提高課堂教學質量與學生參與的積極性。該系統具有兩個方面的功能，第一，可以避免教師在課堂教學中的帶有個人感情色彩的提問偏重，給予每個學生相對均等的回答課堂提問的機會;第二，可以根據學生知識掌握情況以及課堂問題難易程度，適度調節隨機點名的權重分配，提高學生問題回答質量與課堂效率，將課堂提問在教學環節中發揮到最大的作用。

關鍵詞：隨機點名;抽查點名;加權算法;權重分配;課堂提問

中圖分類號：TP311? ? ? ?文獻標識碼：A

文章編號：1009-3044（2021）09-0071-04

開放科學（資源服務）標識碼（OSID）：

Design of Weighted Random Roll Call System Based on MATLAB

HUANG Qiu-hao， REN Cheng-xiang， WANG Xu， CHEN Fei， QIAN Xiang-li

（School of Intelligent Engineering， Shandong University of Management， Jinan 255300， China）

Abstract： Based on the needs of teaching， this paper designs a set of weighted and random classroom questioning systems， the purpose of which is to improve the quality of classroom teaching and the enthusiasm of student participation. The system has two functions. First， it can avoid teachers 'personal emotional questions in classroom teaching， giving each student a relatively equal opportunity to answer classroom questions; second： according to the students' basic knowledge Grasp the situation and the difficulty of classroom questions， moderately adjust the weight distribution of random roll calls， improve the quality of students' question answering and classroom efficiency， and maximize the role of classroom questioning in teaching. Keywords： random roll call random check roll weighting algorithm classroom questioning.

Key words： random roll call; spot check roll call; weighted algorithm; weight distribution ; classroom questioning

1 引言

傳統的課堂提問點名主要有兩種方式，第一種是老師根據學生名單順序依次進行點名提問，第二種是隨機提問。這兩種方法對課堂教學效果的幫助作用都不是特別理想：在第一種方法中，已經被點名并且回答問題的學生，可能出現懈怠聽講的學習狀態[1]，課堂提問不能很好地起到督促學習的效果;在第二種方法中，老師進行隨機提問，則具有主觀性與偏向性，學生很難獲得均等的回答問題機會，使整體的教學質量的提升受到限制[2]。本設計將克服傳統的課堂提問點名形式存在的弊端，引入了加權隨機[3]機制，系統記錄學生以往回答問題的情況，作為其基礎知識掌握情況的反饋，來預測其學習掌握程度，并且結合課堂問題的難易程度，設定每位同學回答當前問題的概率權重[4]大小，一方面能夠以隨機的方式進行點名提問，很好地起到督促學生認真聽講的功能，另一方面能夠讓每個學生獲得均等的回答問題機會及適合的問題，從而提高課堂教學效率[5]，同時可以幫助學生建立學習的自信心。課堂點名提問系統以學生為中心，從重視學生的學習過程為出發點，提升課堂教學的質量。

2 數學模型

2.1 加權概率模型

本系統在每次分配題目并進行提問時，動態計算每位學生針對當前題目被提問的概率。此概率取決于學生已回答問題的次數、近期答題表現，及本次問題的難度等因素。

記學號為i的學生的答題總次數為di，得分評價為ci，答題用時評價為mi，本次題目難度評價為? Ai。所有參數在原始數據基礎上，進行標準差標準化處理[6]，以統一數據尺度。

定義概率影響因子[σi][7]為第i位同學的近期表現及本次題目的難度對 其被抽取概率的影響，則計算公式如下。

[σi=wddi+|1/（wcci+wmmi+waAi+ε）|]? ? ? ? ? ? ? （1）

其中，[wd]、[wc]、[wm]、[wa]、[ε]根據經驗設置為-1、1、1、2和0.5，使得學生已回答次數與被抽取概率負相關，學生近期學習狀況和題目難度的吻合度與被抽取概率正相關。

對全班所有n位學生的[σi]進行歸一化，得到每位學生被抽取回答問題的概率。本系統采用softmax進行歸一化，如公式（2）所示。

[Pi=eσi/j=1neσj]? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? （2）

2.2 權值更新

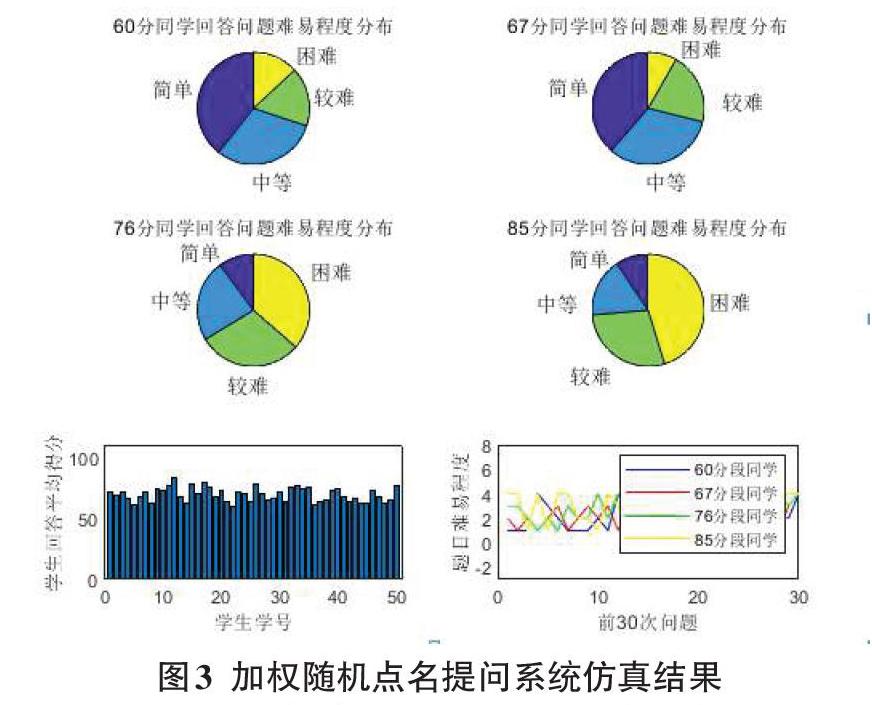
若本次提問抽中第i位學生，則該學生回答問題后，系統對其概率影響因子[σi]中的得分評價ci、答題用時評價mi 及回答總次數di 進行更新。為鼓勵學生進步，在對得分評價ci和答題用時評價mi 的更新中，更注重近期表現。引入衰減系數decay，0

[ci=decay×ci-1+（1-decay）×c]? ? ? ? ? ?（3）

[mi=decay×mi-1+（1-decay）×m]? ? ? ? ? （4）

3 Matlab程序設計

本系統操作簡單，運行穩定，系統設計思路如圖1所示，第一次進入系統后，導入學生學號姓名及初始成績，分配所提問問題難度，計算并對學生的di 、ci? 、mi 、Ai? 進行標準化，然后計算出每位同學對應本次題目的概率因子，從而分配每位同學被提問到的概率，并將被抽取學生本次回答問題的情況記錄到數據庫中，方便后續統計和分析學生的平時成績。

4 仿真結果與分析

4.1 模擬仿真傳統隨機點名提問實驗

作為對比試驗，本文首先假設所有學生每次提問時di、ci、mi、Ai等因素對答題概率沒有影響，即每位同學被提問到的概率相等。

假設提問的總人數x為50人，隨機抽取10000次作為統計數據，觀察每位同學的初始成績對應的回答問題次數，平均得分，回答時間分布以及回答問題難度分布情況，其中，在觀察不同成績同學回答問題難度分布的實驗中，從60-100分之間抽取了初試成績分別為60分，67分，76分，85分的同學作為抽查樣本，仿真結果如圖2所示：

從上述仿真結果中不難看出，不論學生成績如何，其回答不同難度問題的次數基本一樣，沒有做到科學分配，水平低的學生回答困難問題得分較少甚至回答不上來，最終平均分差距較大，進而影響學生的信心，不利于班級向好向上發展。表1可以綜合反映上述問題的弊端。

4.2模擬仿真加權隨機點名提問實驗

本仿真實驗中，令學生人數x仍然為50人，抽取次數仍然為10000次，采取加權隨機點名的方法，即每位學生的答題概率會根據di（前k節課學生回答問題次數）、ci （近期得分情況）、mi? （近期答題用時情況）、Ai? （當前題目難度）進行計算，并根據每次回答情況通過公式（3）和公式（4）進行參數更新。在以上條件下，測試不同成績學生回答問題難度的分布時，仍然從60-100分之間抽取了初試成績分別為60分，67分，76分，85分的同學作為抽查樣本來觀察，與傳統隨機點名提問系統進行對比，仿真圖如圖3所示：

根據圖3得到的仿真結果，不難看出，如果加入di（前k節課學生回答問題次數）、ci近期得分情況）、mi（近期答題用時情況）、Ai（問題難度情況）等參數，并根據這些參數計算答題概率，則可以避免成績和回答問題難度不匹配問題;通過參數更新，能夠動態適應學生的學習狀況，從而幫助學生建立學習的自信心，提升課堂教學的質量，有利于班級更好的發展。表2反映了部分學生各個因素的總體情況，能夠更清晰地反映出該加權隨機點名系統的這方面的優越性。

4.3 本章小結

本章就課堂隨機點名提問系統建立的模型進行仿真與分析，如圖3所示，通過對比試驗可以看到，加權隨機點名提問系統能夠有效提高課堂教學效率，幫助學生建立學習的自信心，提升課堂教學的質量。

5 結束語

加權隨機點名提問系統具有很好的體驗感，方便快捷，有效節省了老師傳統的上課點名所浪費的時間，不但提高了課堂教學質量與學生參與的積極性，而且還有效避免了教師在課堂教學中帶有個人感情色彩的提問偏重，給予每個學生相對均等的回答課堂提問的機會。另外老師還可以根據學生知識掌握情況以及課堂問題難易程度，適度調節隨機點名的權重分配，提高學生問題回答質量與課堂效率，將課堂提問在教學環節中發揮到最大的作用。

參考文獻：

[1] 蘇文敏.初中化學教學中課堂提問的有效性思考[J].中國農村教育，2020（6）：124-125.

[2] 朱家龍.基于Visual Basic的隨機提問系統的實現與教學應用[J].電腦知識與技術，2019，15（15）：148-149.

[3] 胡嬋娟，于蓮芝，薛震.基于Spark框架的用于金融信貸風險控制的加權隨機森林算法[J].小型微型計算機系統，2020，41（2）：369-374.

[4] 高兵，孫琳，謝彪，王文佶，等.權重概率主成分分析模型的建立及應用研究[J].中國衛生統計，2018，35（6）：802-805.

[5] 楊爽.大數據時代課堂教學效率提升策略研究[J].才智，2020（5）：123-124.

[6] 范德輝，李曉林.歸一化加權平均算法在溫度采集系統中的應用[J].機械工程與自動化，2012（3）：115-116+118.

[7] 文亞鳳，崔亮節，孫毅，等.考慮狀態概率因子和狀態修正的非侵入式負荷分解方法[J].電網技術，2019，43（11）：4178-4184.

【通聯編輯：王力】