物理學中常用的高斯與類高斯型積分
王 蒙,陶俊琦,程劍劍,鄭 華
(陜西師范大學 物理學與信息技術學院,陜西 西安 710119)
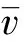
本文旨在基于大學數學基礎對常用的高斯及類高斯型積分做系統的闡述,給出相應的求解方法和通用積分結果. 以期助力學生學習與教職人員教授相關內容.
1 高斯與類高斯型積分
本節中,我們將對不同的高斯與類高斯型積分進行計算與討論,遵循由簡到難、由特殊到一般的邏輯.
1.1 高斯型積分I=e-αx2dx,(α>0,α∈R)
在高斯與類高斯型積分中,非常重要的一個積分是

(1)
考慮α為實數的情況.為保證式(1)積分收斂,要求α>0. 式(1)無法利用牛頓萊布尼茲公式求出原函數對積分進行計算. 但可以通過構造的方法,建立式(1)與二維積分的聯系,然后利用常用積分就可以計算了. 具體過程如下

(2)
對式(2)中r的積分進行變量代換,容易看出是一個指數函數積分. 因此
(3)
此積分過程中體現了一個重要的思想,在當前維度下如果解決不了問題時,可以發散性的將問題向高維轉化.某些特殊函數的生成函數,也應用了這一思想,在此我們不做詳細論述[7].
下面討論3個常用的高斯型積分.
(a) 當α=1時,由式(3)可得
(4)
(b) 將式(3)的積分限變成0到正無窮,由式(3)的積分函數是偶函數可得
(5)
(c) 將式(3)的積分限變成0到正無窮且α=1
(6)
1.2 Γ函數與高斯型積分
Γ函數與高斯型積分具有直接的聯系[8-10].在實變函數中,Γ函數的通常定義如下
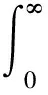
(7)
Γ函數具有如下性質
Γ(x+1)=xΓ(x)
(8)
將Γ函數式(7)的積分變量t作積分變量代換,令t=u2.可得
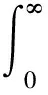
(9)
為便于文章后面的討論,將式(9)改寫為
(10)
可見,當x=0時,式(10)右邊為高斯型積分式(6),故有
(11)
這是我們熟知的結果.
1.3 高斯型積分
下面將考慮幾個不同積分限的高斯型積分.
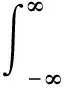
與高斯分布相關的物理量的計算中,很常用的一類積分為

(12)
當n為奇數時,由于被積函數為奇函數,可得

(13)
當n為偶數時,取n=2k(k為自然數),式(12)變成

(14)
我們將以k=1為例,通過3種方法來計算I(2),然后給出積分式(14)的通用公式.
(a) 計算積分I(2)常用的方法為分部積分法
(15)
已經利用了高斯型積分式(3)的結果.如果k值取更大,用分部積分法計算式(14)會比較繁瑣.
(b) 另一種方法計算積分I(2),可以將α看成變量
(16)
此方法比分部積分法簡潔,更重要的是其可以很容易給出積分式(14)的通用公式
(17)
雙階乘定義:(2n-1)!!≡1·3……(2n-3)(2n-1).
(c) 更簡潔的方法是將I(2)與Γ函數式(10)聯系,可得
(18)

(19)
最后的結果已經利用Γ函數的性質式(8).此方法避免了(b)中對α求導的過程.
綜上所述,式(12)的積分結果為
(20)
其中k為自然數.
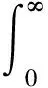
由上節可知,將高斯積分與Γ函數聯系是很簡潔的方法.與式(20)類似的過程可得
(21)
其中k為自然數.
1.4 類高斯型積分I=e-α(x+c)2dx
現在來計算類高斯型積分

(22)
其中α與c可以是復數,考慮到積分的收斂性,要求Re(α)>0. 這與1.1與1.3中要求α為實數不一樣,我們稱之為類高斯型積分.
由于類高斯型積分已經涉及到了復數,有些計算過程會用到“數學物理方法”中的留數定理[11].為使討論更為清晰,我們分以下幾種情況:
(a)α與c均為實數: 這種情況與1.1的討論很相似,唯一的差別是高斯函數的對稱中心在x=-c.可以通過積分變量代換將式(22)變成式(3)

(23)
(b)α為實數,c為純虛數:這種情況下需要用到留數定理. 不失一般性的可以令c=ib,b為正實數. 在復平面上選擇積分路徑如圖1所示.
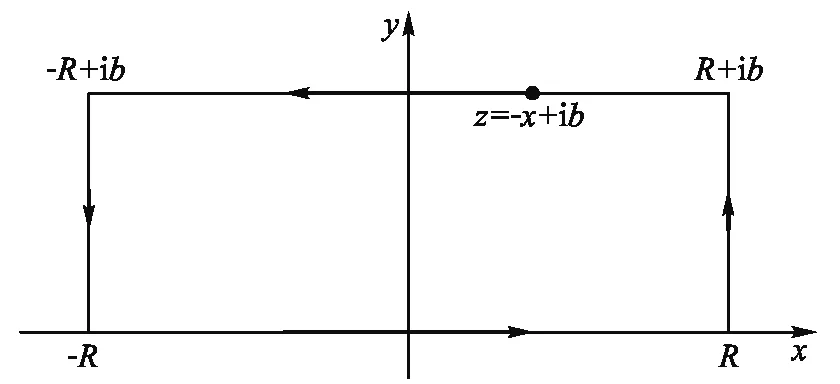
圖1 復平面積分路徑
被積函數f(z)=e-αz2在積分區域內是解析的.由留數定理可得
∮e-αz2dz=0
(24)
可將積分式(24)沿長方形閉合區域寫成4部分之和
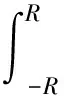
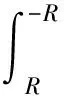
(25)
在R→∞,第三項與待求積分有簡單的關系:
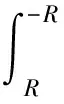
(26)
(27)
當b為負實數時,在復平面上將積分路徑選在下半平面,其余過程與b為正實數類似,可以得到同樣的積分結果.
(c)α為復數,c為實數:α為復數時,與1.1中α為實數時類似,可以得到
(28)
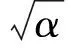
(29)
(d)α為復數,c為純虛數:與1.4 (b)中計算過程類似并利用1.4(c)的積分結果,可得
(30)
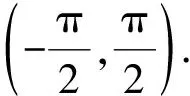
(e)α與c均為復數:此種情況是最一般的情況. 利用1.4 (a)中的積分變量代換,可以將復數c的實部消除,這時積分就變成了1.4 (d)中的積分. 因此,積分結果為
(31)
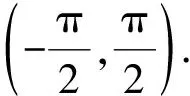

1.5 類高斯型積分I=eim(x+c)2dx



(32)
不失一般性的,先考慮m為正實數. 在復平面上eimz2解析,利用留數定理可得
∮eimz2dz=0
(33)
可在復平面上選擇如圖2所示積分路徑.
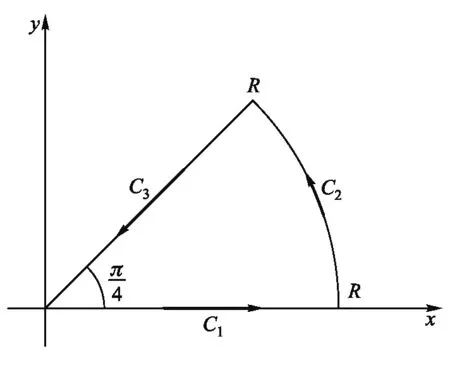
圖2 復平面積分路徑
可將積分式(33)寫成三部分之和
(34)
當R→∞時,式(34)第一項為I/2, 其中I為待求積分;第二項積分為0,計算如下
(35)
第三項積分為
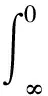
(36)
由式(34)可得
(37)
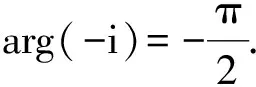
當m為負實數時,在復平面上將積分路徑選在下半平面,其余過程與m為正實數類似.為方便,我們讓m=-m′(m′>0),可得
(38)
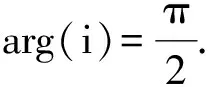
(39)
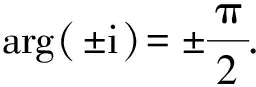
(b)c為純虛數:不失一般性的可以令c=ib,b為正實數. 在復平面上選擇積分路徑如圖1所示,同1.4(b)類似有
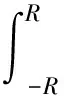
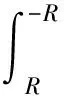
(40)
當R→∞時,式(40)第一項可以利用1.5(a)的結果,第三項等于負的待求積分,考察第二項與第四項的模可以發現總有一項是發散的. 因此,此種情況下待求積分是發散的.
(c)c為復數:此種情況是最一般的情況. 利用1.4(a)中的積分變量代換,可以將復數c的實部消除,這時積分就變成了1.5(b)中的積分. 同樣的道理,此時積分是發散的.
1.6 高斯與類高斯型積分的討論
通過觀察式(3),式(31)與式(39)的積分結果,可以發現高斯與類高斯積分結果均可寫成高斯積分結果的形式,只是需要限定α的輻角范圍:
(a) Re(α)>0,α∈C,c∈C
(41)
需要限定arg(α)∈(-π/2,π/2), 注意α為實數時其輻角為0.
(b) Re(α)=0,α∈C,c∈R
(42)
需要限定arg(α)=-π/2或arg(α)=π/2.
2 高斯與類高斯型積分在物理學中的應用
為將上面討論的高斯及類高斯型積分與物理學科中的實際問題聯系起來,在此我們將選擇不同物理學科中的幾個具體問題,來展示不同形式的高斯及類高斯型積分的應用實例.所選問題的物理內涵及重要性,讀者均可從相應的教科書中查閱.
2.1 熱力學與統計物理[3]
熱力學與統計物理中,在討論麥克斯韋速度分布律及能量均分定理時,需要計算分子速率的平均及分子速率平方的平均 (見文獻[3]中197-200頁).為避免重復計算,我們可先得到速率n次方的平均的通用式
(43)
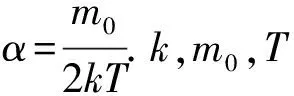
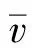
(44)
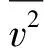
(45)
因此方均根速率為
(46)
2.2 量子力學[1,2,12]
在量子力學中,高斯與類高斯型積分有著廣泛應用.
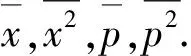
(b) 量子力學中,對同一個問題,可以選擇在不同的表象中求解. 一般情況下,解薛定諤方程是在坐標表象中進行的,但對有些問題在動量表象中求解更方便(見文獻[12]中卷一108-113頁). 一維諧振子既可以在坐標表象也可以在動量表象中精確求解,且在坐標表象中得到的波函數與在動量表象中得到相應的波函數之間可以通過傅立葉變換聯系. 以一維諧振子在動量表象中的基態波函數與其在坐標表象中的基態波函數為例
(47)
由于一維諧振子在坐標表象中基態波函數是高斯函數,傅立葉變換時會出現類高斯型積分
(48)
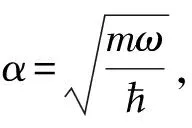
(c) 費曼路徑積分作為量子力學(矩陣力學與波動力學之外)的另一種理論形式,其核心是如何計算量子系統的傳播子.在費曼路徑積分計算自由粒子傳播子的過程中,會用到1.5中討論的類高斯型積分.自由粒子傳播子的計算需要計算兩個高斯函數乘積的積分(見文獻[12]卷二176頁),如下

(49)
其中為α、β純虛數.
3.3 光學[6,11,13]
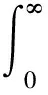
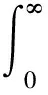
(50)
分別對比式(50)中等式左邊與右邊的實部與虛部可得
(51)
(52)
2.4 量子光學[14]

(53)
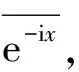
(54)

(55)
3 小結


