基于格蘭杰因果網絡的中美貿易戰對上證行業沖擊的研究*
趙軍產 黃麒安 吳曉群 肖磊
1) (湖南工商大學數學與統計學院, 長沙 410205)
2) (統計學習與智能計算湖南省重點實驗室, 長沙 410205)
3) (武漢大學數學與統計學院, 武漢 430072)
4) (中南財經政法大學統計與數學學院, 武漢 430073)
中美貿易戰對行業沖擊是普遍關注的問題, 本文選取2016 年8 月—2019 年10 月的上證行業指數, 構建了格蘭杰因果關系網絡, 然后結合事件分析法對風險傳播模型的參數進行估計, 最后利用蒙特卡羅算法模擬行業受到貿易戰沖擊后金融風險傳播情況, 并計算貿易戰發生前后的上證股市金融網絡風險傳播的基本再生數.研究發現: 第一, 貿易戰明顯改變了上證行業關系結構, 行業指數之間聯系變得更為緊密; 第二, 貿易戰發生初期, 受美國加征關稅影響, 上證股市感染節點數量迅速增加, 并且感染規模會在第10—15 個交易日內達到峰值, 感染節點數量大約在第25 個交易日后開始趨于平緩, 市場逐漸恢復; 第三, 基本再生數計算結果表明, 上證股市在貿易戰發生初期金融風險傳播較快, 上證股市容易產生“同漲同跌”的現象.
1 引 言
股票市場是一個國家或地區經濟和金融活動的晴雨表, 股票市場容易受到政策性因素的影響,呈現出“同漲同跌”現象, 將股票看成節點, 股票之間的耦合作用抽象成邊, 越來越多的研究者利用復雜網絡模型對股票市場的波動規律進行研究[1?6].邱路和賈天明[7]利用差分網絡來研究金融危機對股票市場中行業的影響, 發現不同金融危機下對行業的影響具有顯著的差異性.Landesberger 等[8]對金融危機在股市中的傳播進行了可視化分析,直觀地展現了網絡中危機擴散的過程.Liu 和Arunkumar[9]對金融危機在股票市場網絡中的傳播機制、傳播效果的測度、傳播路徑和免疫策略進行了實證分析.Gong 等[10]利用傳遞熵構建股票市場網絡, 研究發現在危機爆發的情況下, 股票市場節點會變得更加接近, 連邊也變得更加稠密, 越靠近網絡中心的節點越容易受到沖擊的影響.Wang和Li[11]通過構建多層網絡分析中國的銀行間的風險傳染, 發現衍生市場網絡和銀行內部網絡的結果會影響系統性風險, 銀行網絡密度越大系統性風險越低.考慮到股票間信息的不對稱性, 利用有向復雜網絡能更好地模擬某一重大事件對股票市場的影響, 格蘭杰因果檢測能有效地反映股票A 對股票B 的影響, 因此得到越來越多研究者的關注.Blinowska 等[12]對比了二元格蘭杰和多元格蘭杰信息流動效率, 證明了信息在多元格蘭杰圖上傳播更有效率.Vyrost 等[13]用格蘭杰因果關系分析了2006 年—2013 年全球股票市場的收盤價格, 結果表明金融危機對美國股票市場的沖擊減小了, 在全球范圍內因果聯系越緊密的市場之間的溢出效應越高.自2018 年3 月以來, 中美貿易摩擦逐步升級, 給中美兩國的經濟帶來巨大的影響.目前, 國內外學者主要從宏觀層面研究貿易戰對整個金融市場的影響, 而對行業板塊之間的相互影響以關聯變動的研究較少.貿易戰的主要形式是中美兩國針對特定商品加征進口關稅以及出臺臨時政策限制部分外資企業在本國的擴張, 這些措施都具有較強的目的性, 即在一輪制裁中僅對少數行業的商品和服務進行打擊, 如美國對中國加征的第一輪關稅中主要集中在機械設備、電子設備、運輸設備、醫藥等高端制造業, 第二輪加征的關稅主要集中在化工品和鋼鋁行業, 美國并不會將中國所有出口的商品一律增加關稅, 然而資本市場中各個行業板塊具有高度的相關性, 一個行業板塊的股票價格的劇烈波動可能會引起相關行業板塊股票的價格波動, 甚至可能通過連鎖反應影響到整個金融市場.這為相關研究提供了重要的現實意義, 即分析金融市場中各個行業板塊之間的關聯性, 為金融風險在股票市場中的傳播擴散提供合理解釋.因此, 本文收集中美貿易戰發生前后的我國A 股市場的相關數據, 利用格蘭杰因果檢測法建立貿易戰前后的有向復雜網絡, 對比股票市場行業間的連接變化, 統計兩個時段的網絡特征量, 找出關鍵行業, 借助于SIR傳染病模型, 模擬不同行業受到中美貿易戰沖擊時股票市場風險傳播情況.
2 數據和方法
2.1 數據采集和預處理
申銀萬國二級行業指數是由申銀萬國公司編制, 將上證股市股票劃分為103 個行業, 通過一定的權重比例將各個行業的股票價格轉化成的行業指數, 以反映整體行業的價格變動.本文選取最新2014 年版標準的申萬二級行業指數, 以2016 年8 月25 日—2018 年3 月21 日作為貿易戰開始前的時間段, 去除周末節假日得到382 組數據; 以2018 年3 月22 日—2019 年10 月25 日作為貿易戰開始后的時間段, 去除周末節假日得到389 組數據, 數據來源于Wind 數據庫.進行格蘭杰因果檢驗需要保證時間序列的平穩性, 本節對原始數據對
數收益率化, 計算公式為
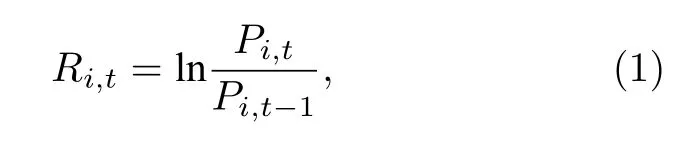
其中Ri,t表示第i個行業指數第t個交易日內的指數自然對數收益率,Pi,t表示第i個行業第t個交易日內的指數收盤價.
2.2 方法與步驟
2.2.1 格蘭杰因果檢測法構建有向網絡
格蘭杰因果是在經濟學中研究兩個時間序列之間關系的有效方法, 其基本原理為給定兩個平穩時間序列Xt,Yt, 其中Yt的自回歸模型預測如下[14]:
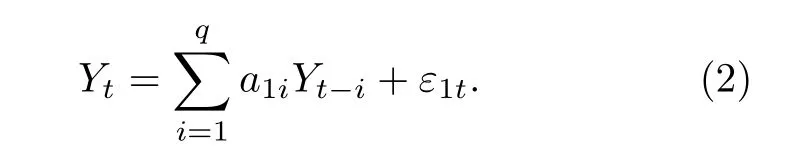
同時, 加入Xt的信息對Yt的預測如下:
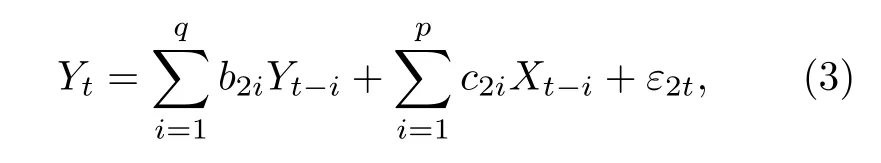
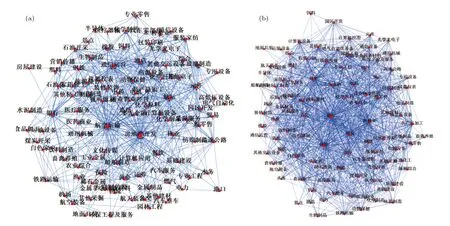
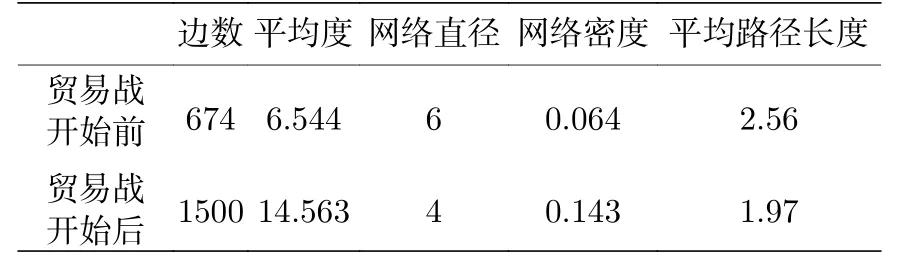
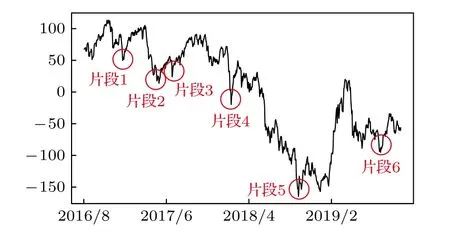
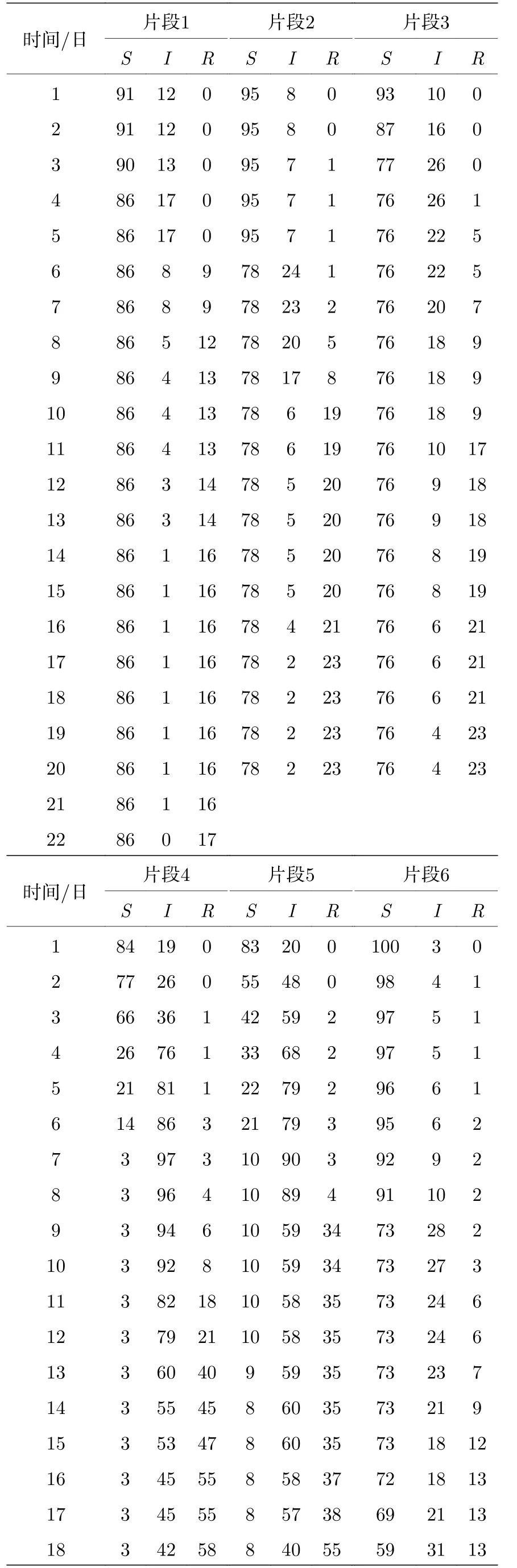
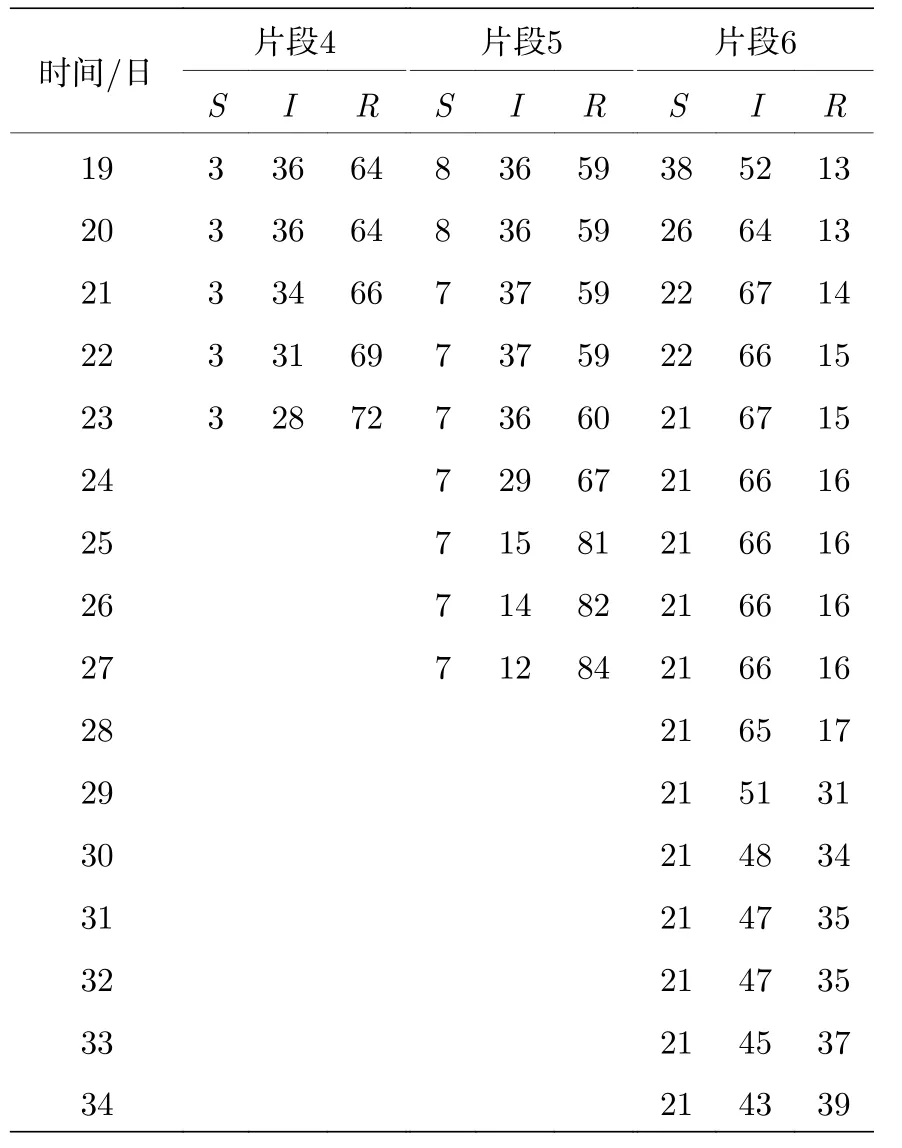
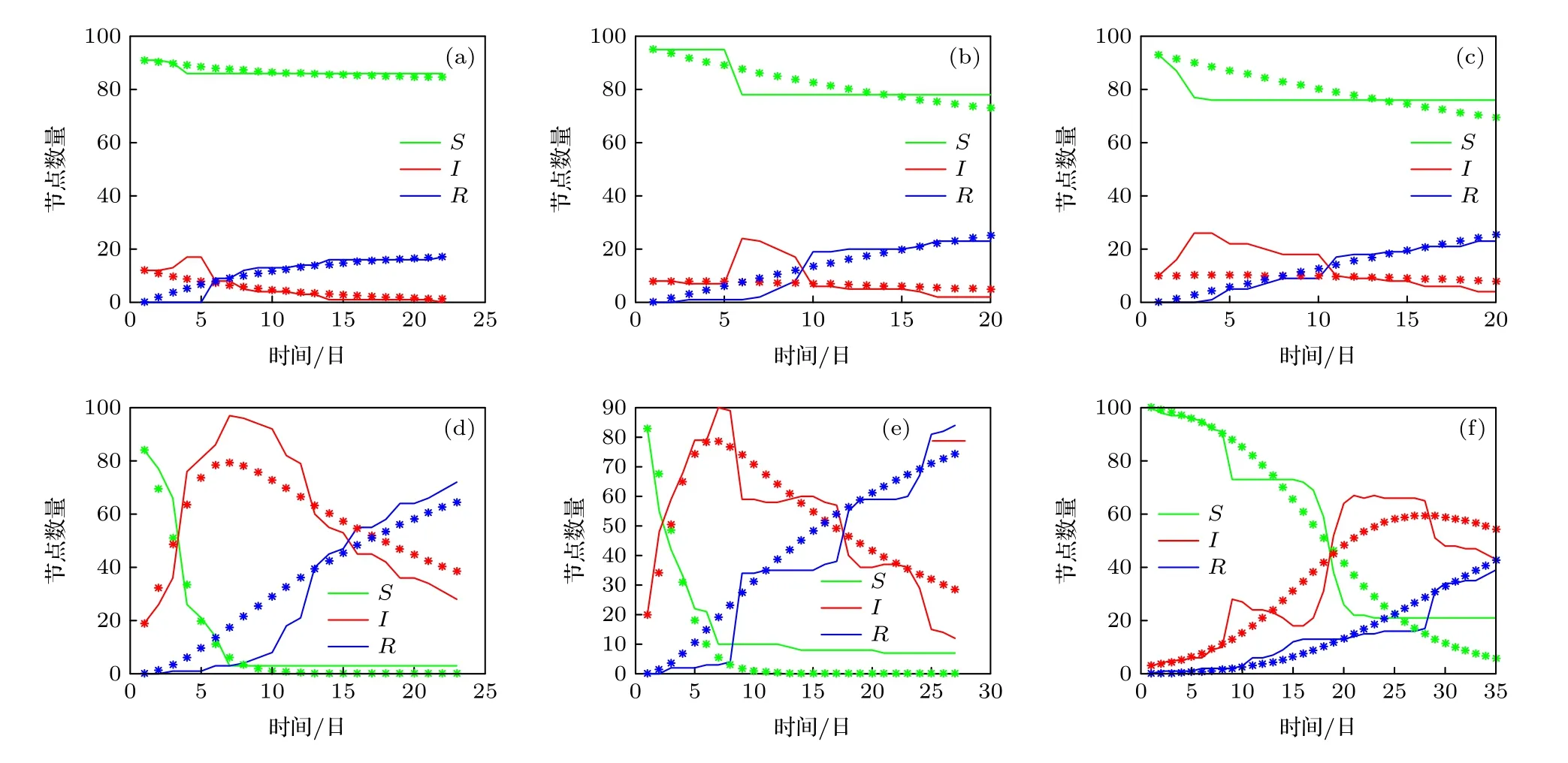
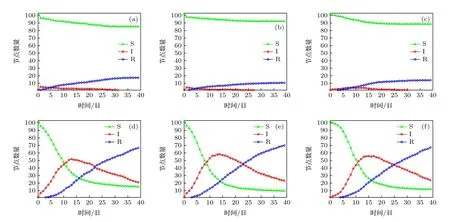
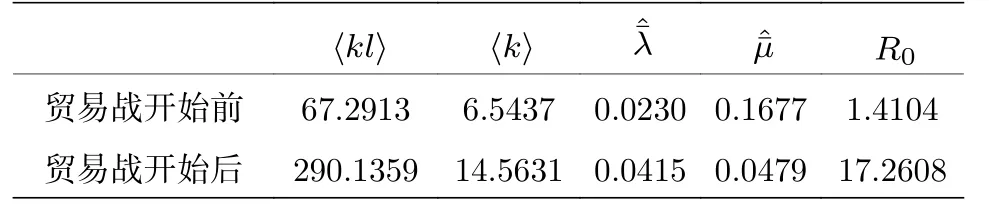
其中,q, p分別代表Y和X的自回歸階數;a1i,b2i, c2i為歸回系數;ε1t, ε2t代表預測誤差.根據格蘭杰因果檢測理論, 如果 V ar(ε2t) 格蘭杰因果檢測法構建有向網絡, 即對面板數據兩兩進行格蘭杰因果檢驗, 通過檢驗在兩節點間添加一條由“格蘭杰因”指向“格蘭杰果”的有向連邊, 循環這一步驟直至所有變量都進行了檢驗, 這樣就得到了有向的格蘭杰關系網絡. 2.2.2 標準SIR 模型和有向SIR 模型的構建與參數估計方法 傳染病模型是信息傳播領域較為成熟的模型[15].隨著研究的深入, 該模型不僅應用到流行病學領域, 在金融風險、社會輿情分析等領域都有廣泛的應用.傳染病模型有很多種類, 如類似于SI 模型的級聯模型[16]、可重復感染的SIS 模型[17]以及基于異構網絡的SIRS 模型[18,19], 大部分都是由標準SIR 模型派生出來的, 標準的SIR 模型為 其中β為有效傳播率;μ為自愈率;s,i,r分別為感染者、易感者和移除者占總體的比例, 并且有s+i+r=1恒成立. (4)式的SIR 模型沒有考慮有向網絡的情況,為了刻畫有向網絡上的風險傳播, 下面介紹有向網絡上的SIR 模型[20]: 其中λ表示接觸傳染率;s(k,l)(t),i(k,l)(t),r(k,l)(t) 表示t時刻下出度為k、入度為l的易感者、感染者和恢復著的相對密度, 并且滿足s(k,l)(t)+i(k,l)(t)+r(k,l)(t)=1 ;θ(t) 為在網絡 中 任 選 一條邊由染病節點出發的概率, 表示為[20] 定義p(i,j) 為網絡中隨機選取一個入度為i、出度為j的節點的概率, 而p((i,j)|(k,l)) 表示網絡中的任一條邊由“度”為 (i,j) 的節點出發, 指向“度”為 (k,l) 的節點的概率. 胡志浩和李曉花[21]認為網絡參數變動帶來的影響已由網絡的基本性質決定了, 網絡中感染擴散的數值會受到參數變化的影響, 但擴散的基本特征不會改變, 因此他們選取參數 (λ,μ) 為(0.24, 0.18)來對金融機構間大額支付網絡的傳播情況進行數值模擬, 在這組參數下, 危機的傳播效果最為顯著.但是影響網絡感染擴散情況的因素除了網絡的基本性質外, 有效傳播率λ和恢復率μ依然很重要,因為有效傳播率和恢復率會直接影響感染數量曲線的形狀, 包括感染數量高峰出現的時間和數值,由于模型(5)是一個十分復雜的多微分方程組模型, 因此本文通過最小二乘法估計模型(4)的參數,然后根據模型(4)和模型(5)的關系間接估計出模型(5)的參數, 最小二乘法擬合的目標是找到合適參數值的最小化總殘差, 即: 其中ST,IT,RT分別為實際片段的易感者、感染者和恢復者數量;S,I,R分別為數值模擬的易感者、感染者和恢復者的數量;n為片段中的交易日總數.容易推得β=λk, 即有效傳播率等于接觸傳播率乘以節點的出度, 于是就可以建立標準SIR 模型與有向SIR 模型參數之間的聯系[20]. 2.2.3 有向網絡上的隨機SIR 模型蒙特卡羅模擬算法 隨機SIR 模型將隨機過程與傳染病模型相結合, 其優點在于考慮了傳播網絡的空間結構.Youssef 和Scoglio[22]利用馬爾科夫鏈個體依賴的方法估計了網絡傳染病中每個個體的概率, 并給出了染病個體最大數目與特征值之間的關系.本文結合參數估計和馬爾科夫鏈個體依賴的思想, 提出了一種有向網絡上的隨機SIR 模型蒙特卡羅模擬算法: 1)構建上證行業指數的格蘭杰因果關系有向網絡; 2)運用最小二乘法估計模型(4)和模型(5)的參數 (λ,μ) ; 3)設置初始狀態, 0 時刻網絡中少數節點設置為感染狀態, 其余的全部為易感狀態, 無恢復狀態; 4)每一輪均以概率λ, 利用感染狀態的節點去感染有向連接下的易感染狀態節點, 產生 [ 0,1] 的隨機數, 如果隨機數小于λ, 則表示感染成功, 同時處于感染狀態的節點以μ的概率變為恢復狀態, 如果隨機數小于μ, 則表示恢復成功; 5)重復步驟3, 直到所有節點變為恢復狀態,傳染結束. 2.2.4 基本再生數 根據靳禎等[20]對有向網絡動力學傳播特點的研究, 模型(5)零平衡點的局部穩定性由下面的方程決定: 其 中Φ=(φ(1,1),φ(1,2),··· ,φ(din,dout))T,φ(k,l)(t)為輔助函數, 由該輔助函數可以構建在時間趨于無窮大條件下的自約束方程Φ=F(Φ) ;λ為接觸感染率;din, dout分別為節點的入度和出度;A為(din×dout)×(din×dout)階矩陣: 矩陣元中的p((i,j)|(k,l)) 表示網絡中的任意一條邊從入度和出度為 (i,j) 的節點指向入度和出度為(k,l) 的節點的概率, 記矩陣A的最大特征值為Λm,當λΛm>1 時, 零平衡點Φ=0 不穩定, 進一步得到傳播閾值為 其中λc為接觸傳染率的閾值, 由于系統傳播的閾值與基本再生數存在等價關系[23] 因此可以得到計算基本再生數的方法.特別地, 在度不相關的條件下, 概率p((i,j)|(k,l)) 只與上游節點有關, 即: 其中p(i,j) 表示節點入度和出度分別為i和j的概率, Tanimoto 在文獻[24]中給出了度不相關條件下閾值的推導, 進一步得到: 最后將(13)式代入(11)式得到度不相關條件下的有向網絡的基本再生數計算表達式: 圖1 上證股市格蘭杰因果網絡圖 (a)貿易戰開始前網絡; (b)貿易戰開始后網絡Fig.1.Granger causality network of Shanghai Stock Market: (a) Before trade war; (b) after trade war. 表1 網絡拓撲結構指標Table 1.Network topology index. 首先將行業指數收益率對數化, 然后進行格蘭杰因果檢驗, 最終構建申萬二級行業指數的格蘭杰因果有向網絡.圖1 給出了貿易戰前后的格蘭杰因果關系網絡, 網絡拓撲結構指標如表1 所列.對比貿易戰前后的網絡結構圖和拓撲結構指標表可以看出, 貿易戰使得行業節點之間連接增多, 連邊數由原來的674 增加到1500, 節點之間的距離也變小, 平均路徑長度由原來的2.56 減少到1.97, 整個上證股市的聯系變得更加緊密, 網絡密度由原來的0.064 增加到0.143. 金融網絡上的傳染病參數估計需要解決如下兩個問題: 1)確定危機發生的時間; 2)確定危機時間段內不同狀態節點的劃分.具體做法是: 首先對103 個申萬二級行業指數全部標準化處理, 并將同一時間下的指數相加, 得到一條反映總體指數變動的時間序列, 如圖2 所示; 然后從圖中直觀選取有較大跌幅而后又反彈的時間片段作為擬合的對象,這些片段可以看作是上證股市受到外部沖擊, 感染從擴散到消失的過程.經過整理和篩選, 找出了6 個代表性的片段, 其中片段1 發生在2017 年1 月和2 月, 片段2 發生在2017 年5 月和6 月, 片段3發生在2017 年7 月, 這幾次下跌中創業板股票和新股是最慘烈的, 業內人士認為原因是證券監管層的新股發行常態化政策.片段4 發生在2018 年2 月, 此時美國發起的針對中國出口的“301 調查”正在進行中, 中美貿易戰不斷醞釀及人民幣的不斷貶值都成為此次上證大跌的導火索.片段5 發生在2018 年10 月, 業界認為這次上證股市大跌是由于美股暴跌導致全球各市場股票大跌, 美國國債的預期收益率提升和美聯儲加息政策成為此次事件的誘因.片段6 發生在2019 年8 月, 股市大跌的原因與片段5 類似, 都是由美股領跌引起的. 圖2 標準化后的行業綜合指數Fig.2.Standardized industry composite index. 截取了行業指數的時間片段后, 下一步需要對SIR 感染狀態進行劃分, 目前對金融風險傳播主要運用數值模擬的方法進行研究, 對于股票下跌幅度達到多少可以算作是受到系統性金融風險的影響, 暫無明確的標準.本文是從實際的日交易數據出發, 在確定感染狀態和恢復狀態的臨界值上有一定難度.股市的熔斷機制是指當股指波幅達到規定的熔斷點時, 交易所為控制風險采取的暫停交易措施.熔斷機制為市場投資者提供了終止交易的冷靜期, 以防股票價格的劇烈波動和恐慌性拋售[25].因此熔斷機制的臨界值對本文感染狀態劃分的臨界值的選取有一定參考價值.目前, 上證股市采用的是5%和7%的兩檔熔斷值.綜合考慮, 選擇–7%和–5%作為劃分狀態的臨界值, 即與初始值相比, 若一個行業指數的跌幅超過7%, 則認為該行業受到了感染, 若一個行業指數的跌幅由原來的超過7%下降到5%以內, 則認為該行業從危機中逐步恢復, 計算分析后得到表2 所列數據.表2 中的S,I,R分別代表易感者、感染者和恢復者的數量. 經過擬合, 片段1 得到的擬合參數[]=[0.0731,0.1667] , 片 段2 得到的擬合參數[]=[0.2113,0.1956] , 片 段3 得到的擬合參數[]=[0.1659,0.1409] , 片 段4 得到的擬合參數[]=[0.7784,0.0.0504], 片段5 得到的擬合參數[]=[0.7966,0.0541] , 片 段6 得到的擬合參數[]=[0.2358,0.0392].得到的擬合圖如圖3 所示, 由于片段4 發生的時間剛好處于美國發起的“301 調查”之時, 所以按照發生時間劃分, 把片段1—3 歸類為貿易戰發生前, 而把片段4—6 歸類為貿易戰發生后.將片段1—3 的參數求平均值得到[]=[0.1501,0.1677], 將片段4—6 的參數求平均值得到[]=[0.6036,0.0479].利用網絡的平均出度代替k, 貿易戰前后的網絡平均出度分別為6.54 和14.56, 經計算, 貿易戰前后上證網絡的接觸感染率分別為0.0230 和0.0415, 自愈率分 別 為0.1677 和0.0479. 美國對中國發起的關稅制裁是有行業傾向性的, 從美國公布的加征關稅的中國商品清單可以看出, 美國對中國加征的第一輪關稅主要集中在機械設備、電子設備、運輸設備、醫藥等高端制造業; 第二輪加征的關稅中, 化工品和鋼鋁等工業金屬所占條目最多.考慮到加征關稅的商品所屬的行業具有聯系與區別的特點, 本文將聯系緊密的行業作為初始傳染源進行一次傳染模擬, 這樣比較符合關稅事件對行業造成沖擊的狀況, 所以選擇化學制藥、中藥、生物制品、醫療器械、醫療服務作為第一次的傳染源, 通用設備、專用設備、儀器儀表、運輸設備作為第二次的傳染源, 鋼鐵和工業金屬作為第三次的傳染源, 再分為貿易戰發生前和貿易戰發生后兩種情況, 取100 次模擬狀況的平均值繪制成圖4.從圖4 可以看出, 貿易戰發生前上證股市的風險是不易擴散的, 面對沖擊只有少數行業會受到感染,并且能在大約30 個交易日完全恢復.然而貿易戰發生后風險變得容易擴散了, 感染節點的峰值發生在沖擊后第10—15 交易日之間, 隨后逐漸下降,大約在第25 個交易日開始趨于平緩.這表示上證股市受到沖擊后, 危機會迅速擴散開來, 在10—15 個交易日內達到最大的影響規模, 整個擴散過程會在25 個交易日左右結束, 隨后上證股市逐漸從危機中恢復.另外觀察到, 趨于穩態時, 有大約10%的節點是沒有被感染的, 這意味著上證股市網絡中存在少量不容易受到大盤影響的行業節點. 表2 SIR 狀態劃分表匯總Table 2.Summary table of SIR status. 表2 (續) SIR 狀態劃分表匯總Table 2 (續).Summary table of SIR status. 圖3 參數擬合 (a)片段1 擬合圖; (b)片段2 擬合圖; (c)片段3 擬合圖; (d)片段4 擬合圖; (e)片段5 擬合圖; (f)片段6 擬合圖.其中實線表示實際曲線, 星號表示擬合曲線Fig.3.Parameter fitting: (a) Segment 1 fitting plot; (b) segment 2 fitting plot; (c) segment 3 fitting plot; (d) segment 4 fitting plot;(e) segment 5 fitting plot; (f) segment 6 fitting plot.Solid line represents actual curve, asterisk represents fitting curve. 圖4 有向網絡下的模擬傳染擴散 (a), (d)貿易戰發生前后生物醫藥類行業為傳染源的擴散圖; (b), (e)貿易戰發生前后家機械設備類業為傳染源的擴散圖; (c), (f)貿易戰發生前后鋼鐵和工業金屬行業為傳染源的擴散圖Fig.4.Simulation of contagion diffusion in directed networks: (a), (d) Diffusion charts of biomedicine before and after the trade war; (b), (e) diffusion charts of mechanical equipment industry before and after the trade war; (c), (f) diffusion charts of steel and industrial metal industries before and after the trade war. 本節根據上文介紹的有向網絡的再生數計算方法, 計算得到上證股市傳染基本再生數(表3).“羊群效應”是指經濟個體的從眾跟風現象.Zhu等[26]利用回歸模型研究了不同時期的中國股市股票收益率, 指出“羊群效應”現象顯著存在于中國股市行業中.“羊群效應”會引發上證股市中大量資金同時流入或者流出, 直接導致股票“同漲同跌”.從表3 可以看出, 貿易戰前上證股市具有較小的R0值, 風險不易在市場中擴散, 而貿易戰后上證股市的R0值明顯增大, 這表明貿易戰后金融沖擊傳染是容易在上證股市中擴散的, 整個上證股市具有較大的系統性金融風險, 也從基本再生數的角度驗證了貿易戰后上證股市容易產生“同漲同跌”的現象. 表3 上證股市傳染基本再生數Table 3.The basic recurrence number of contagion in Shanghai Stock Market. 本文利用有向網絡上的隨機傳染病模型, 結合蒙特卡羅算法模擬中美貿易戰對上證行業的沖擊,該算法比傳統的SIR 微分方程模擬更加具體和可靠, 模擬結果表明: 1)貿易戰發生前, 金融沖擊不易在上證股市中擴散, 并且市場能夠在30 個交易日內將沖擊消化, 然而貿易戰發生后, 金融沖擊容易在市場中擴散, 上證市場各個行業間的聯系也變得更加緊密; 2)貿易戰發生后, 上證股市受感染行業數量會在初期快速增加, 然后會在第10—15 個交易日內達到最大的感染規模, 易感染數量大約在第25 個交易日后趨于平緩, 這表明從金融沖擊產生到消失的整個過程會持續約25 個交易日, 隨后市場逐漸從金融沖擊中恢復, 并且始終有大約10%的少數行業節點在市場中保持相對獨立, 不易受到其他股票波動的影響; 3)實證數據分析顯示,貿易戰前后金融網絡傳染的基本再生數分別為1.4104 和17.2608, 這表明貿易戰后上證股市的系統性金融風險增大, 從基本再生數的角度驗證了上證股市容易產生“同漲同跌”的現象. 復雜系統可以挖掘和解釋元素之間的內在關系, 本文利用格蘭杰因果網絡結合傳播動力學原理分析了上證股市網絡的擴散狀況, 但是不足之處在于沒有根據網絡的具體情況研究政府針對性的免疫策略, 這也是我們接下來的研究工作.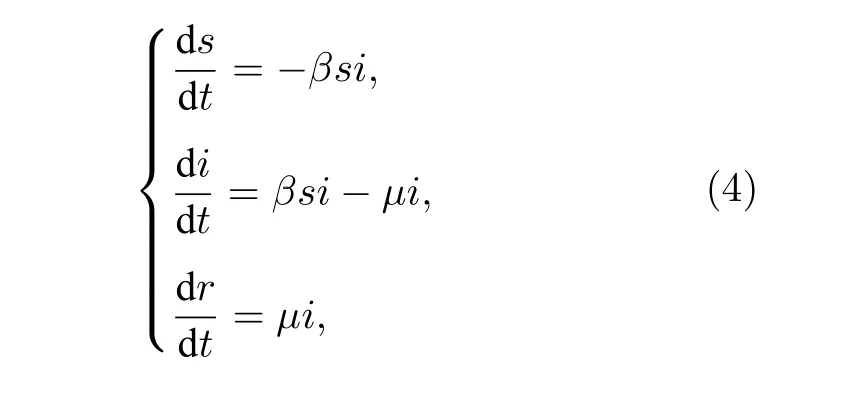
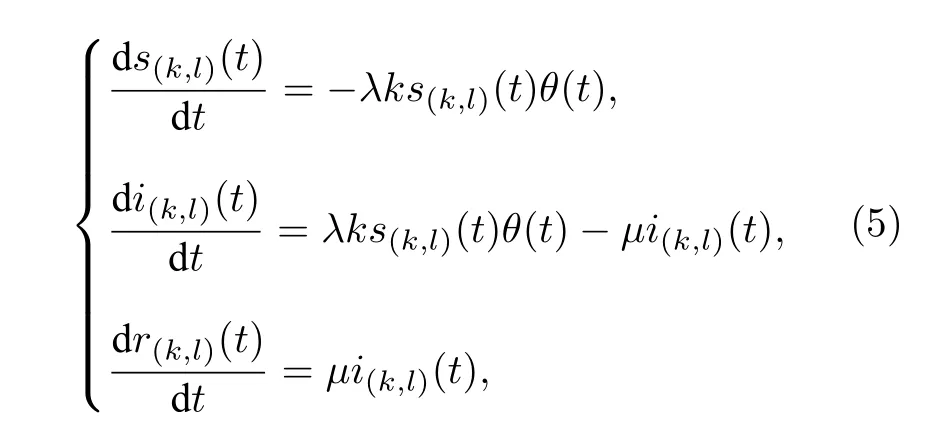
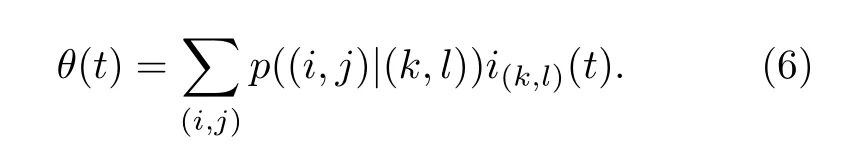
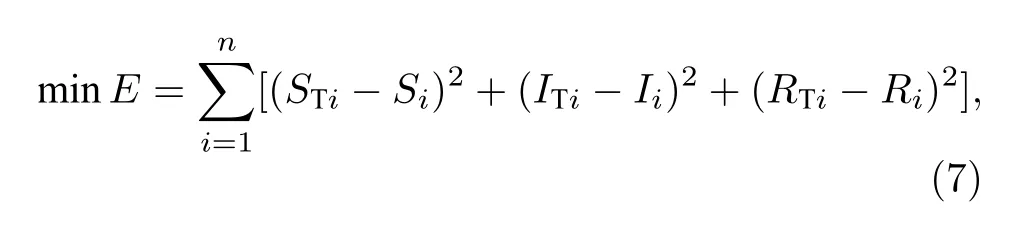
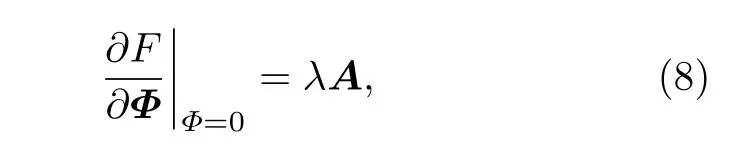



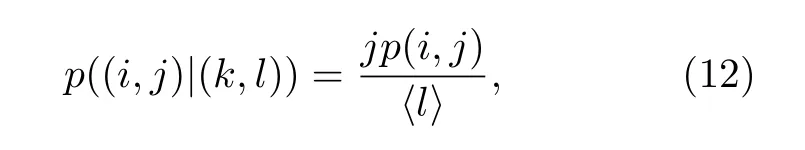
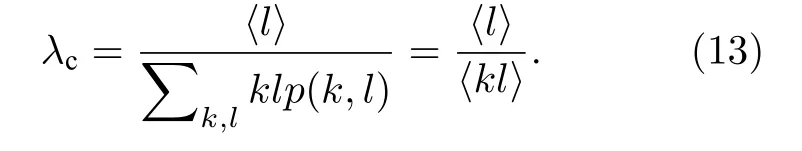
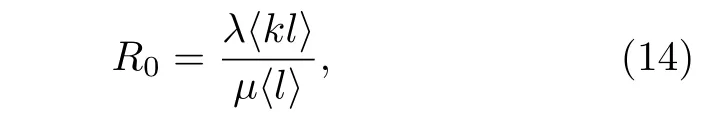
3 實證分析
3.1 格蘭杰因果網絡構建
3.2 參數估計
3.3 傳染擴散模擬
3.4 傳播基本再生數
4 結論與建議

