柱-環梁法對料倉框架結構地震響應研究

于 洋，劉占宇，梁 豪

(東北石油大學 土木建筑工程學院，黑龍江 大慶 163318)

料倉作為一種常見的存貯工業建筑，廣泛應用在我國石油化工、糧食存貯行業。而在料倉實際設計過程中，由于缺少相應的行業標準與規范為依據，不同設計人員對規范的使用和理解存在很大的差異，主要反映在配筋相差較大，約有20%～30%，造成很大的浪費，也增加了施工難度。國內外研究人員從工程實際出發，進行料倉優化設計方面的研究，并取得了豐富的成果，提供許多可供研究的案例，國內外規范對料倉-框架結構的設計方法也作了許多規定[1-13]，但是目前還沒有一個廣為接受的設計方法。理論方面國內外學者也進行了許多研究，1895年，德國學者Janssen[14]提出著名的Janssen物料壓力公式，該公式簡便易操作，與實際受力較為吻合，時至今日還被許多國家所采用，并被應用到筒倉設計規范中，是筒倉方向研究的基石。近些年來，有學者研究由波紋壁和立柱組成的圓柱形鋼筒倉在整體荷載作用下的整體穩定性及優化設計。利用單位柱抗彎剛度變化引起的屈曲荷載系數的影響線，對每個設計階段筒倉柱截面的變化進行了計算[15]，用理想筒倉三維殼體模型的線性屈曲有限元分析結果和幾何非線性有限元分析ABAQUS進行了驗證，根據計算結果提出一種合理的筒倉設計方法。國內較為有代表性的研究也有很多，有分析內部散裝物料的相關實驗研究、筒倉結構的相關實驗研究[16-17]。還有利用有限元軟件ABAQUS將框架與料倉相結合的綜合分析，得出更為深入的研究結論[18]。

本文在已有研究的基礎上，結合工程實例，選擇適合的結構方案，合理簡化計算模型，在滿足構造要求的基礎上合理配置鋼筋，不僅減小施工過程中的造價，更能提高結構的安全性。同時，為制定相關的行業設計規范提供一定的理論依據。

1 柱-環梁法料倉剛度等效理論

料倉體積龐大，而且高度較大，固定在結構上后實際上已融為一體，因此結構分析時應采用一體的結構計算模型，故料倉結構在分析過程中，為了模擬工程實際情況，將料倉簡化為由八根方柱和幾層環梁組成的一體柱環梁-框架結構[18]，詳見圖1所示。

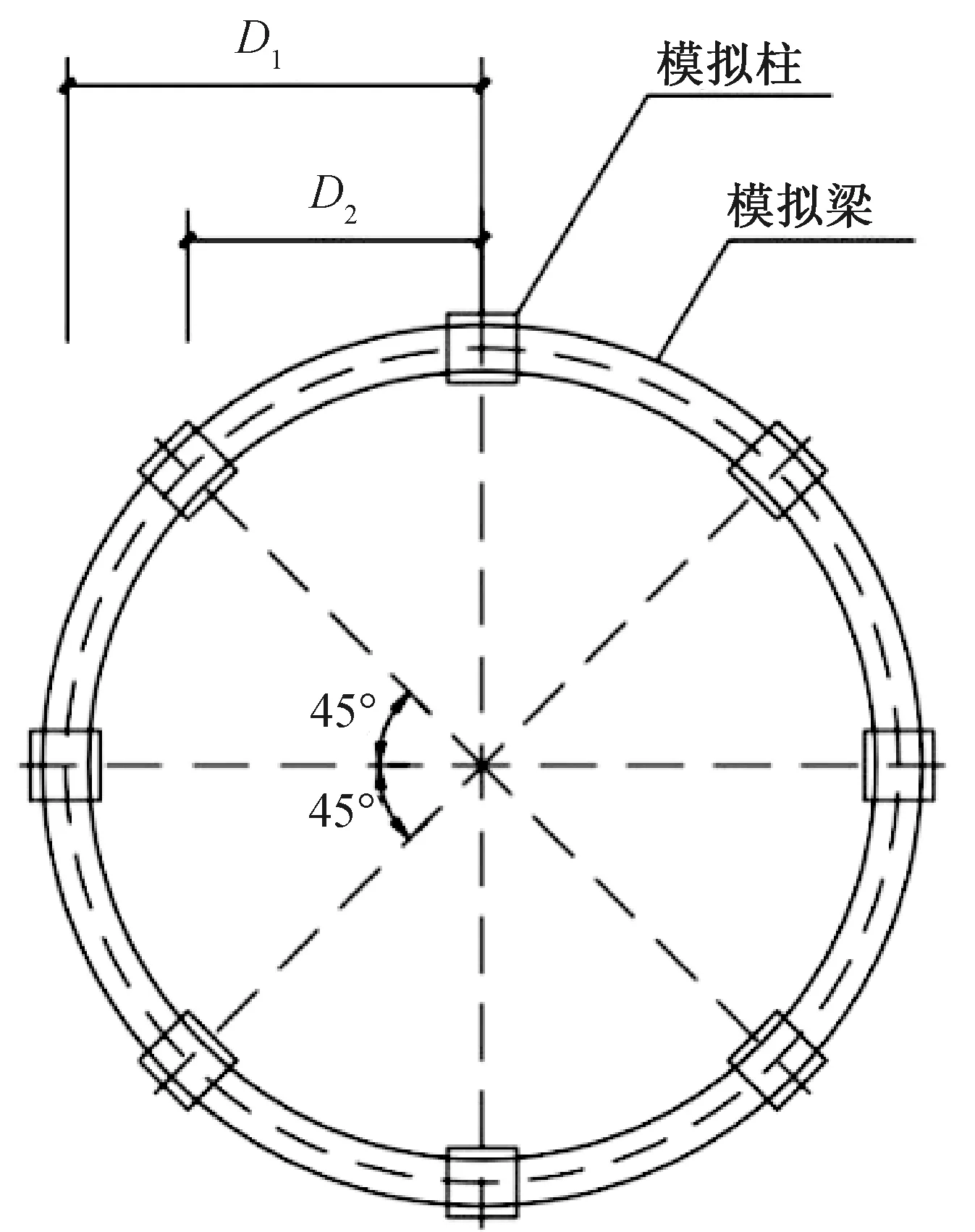
圖1 柱環梁模擬圖Fig.1 Column ring beam simulation diagram

根據平面剛度等效原則：

得出

其中：d2—料倉外徑，d1—料倉內徑，Es—鋁合金彈性模量，Ec—混凝土彈性模量，b—方形柱邊長，D1—相鄰柱中心水平間距，D2—間隔柱中心水平間距。

擬結合某石化公司脫氣及儲存料倉-框架結構項目，已知料倉外徑為7 216 mm，內徑為7 184 mm，鋁合金的彈性模量為7.0×104N/mm2，鋼筋混凝土的彈性模量為3.25×104N/mm2，相鄰柱中心水平間距為2 546 mm，間隔柱中心水平間距為3 600 mm，不計柱本身慣性矩。

計算建模b取值為312 mm，建模取400 mm。為了模擬準確，將料倉上部劃分六等分，每隔4 m設置一環梁，共六道環梁，環梁截面為400 mm×400 mm。

2 分析結構的選取及模型的建立

2.1 材料參數的選取

擬結合某石化公司脫氣及儲存料倉-框架結構項目，已知料倉外徑為7 216 mm，內徑為7 184 mm，鋁合金的彈性模量為7.0×104N/mm2，鋼筋混凝土的彈性模量為3.25×104N/mm2，相鄰柱中心水平間距為2 546 mm，間隔柱中心水平間距為3 600 mm，不計柱本身慣性矩。

料倉-框架結構主要包括上部料倉，下部框架結構及其附屬設施，其長×寬×高為45 m×18 m×39 m，如圖2所示。該結構由兩排十個單料倉-框架組成，料倉直徑7.2 m，倉壁厚度0.16 m，料倉高度24 m，錐底部分高度8 m，框架部分長度9×5=45 m，寬度9×2=18 m，高度分兩層，底層高6.2 m，二層高8.8 m。

該料倉-框架結構設計主要使用鋁合金、鋼筋和混凝土，材料的力學性能參數見表1。

表1 材料的力學性能參數

圖2 料倉實際結構圖Fig.2 Actual structure of silo

表2 結構有限元分析模型單元

圖3 結構的有限元建模Fig.3 Finite element modeling of structures

圖4 柱環梁尺寸、道數的調整后的有限元模型圖Fig.4 Finite element model drawing after adjusting the size and number of beams

2.2 有限元模型的建立

模型驗證選取單料倉框架進行分析，在建立料倉-框架結構有限元分析模型時，忽略接管、法蘭、預埋套管等附屬設施，有限元模型各部分單元選取見表2。

料倉倉底部按固定約束端處理，采用自底向上的建模方式建模。首先定義關鍵點，然后連接線段、繪制成面，再生成三維實體模型。原單料倉-框架結構和單柱環梁-框架結構有限元模型如圖3所示。

2.3 柱環梁的調整

利用剛度等效公式，計算得出柱環梁的截面尺寸寬×高為400 mm×400 mm，根據本工程需要，設計以柱環梁道數為六道，將料倉上部劃分六等分，每隔4 m設置一環梁。同時建立截面500 mm、600 mm尺寸柱環梁-框架結構有限元模型，與原模型進行對比分析。同時分別建立四道柱環梁、六道柱環梁和八道柱環梁的柱環梁-框架結構有限元模型，進行對比分析研究。尺寸為400 mm的柱環梁模型如圖4所示。

3 結構自振特性分析

由表3可知，原料倉-框架結構模型自振頻率為1.783 8 Hz，柱環梁尺寸為400 mm時，柱環梁框架結構自振頻率為1.310 2 Hz，柱環梁尺寸調整為500 mm時，柱環梁框架結構自振頻率為1.530 3 Hz，柱環梁尺寸調整為600 mm時，柱環梁框架結構自振頻率為1.472 7 Hz。因此，在柱環梁尺寸為500 mm時，與原模型自振特性更為接近。

設定柱環梁尺寸為500 mm，調整柱環梁道數。柱環梁道數分別選取為4道、6道和8道，柱環梁道數不同情況下的結構自振頻率如表4所示。由表4可知，當環梁道數為六道時，柱環梁框架結構自振頻率(1.530 3 Hz)與原料倉-框架結構模型自振頻率(1.783 8 Hz)最為接近。

經過以上計算得知，柱環梁-框架結構在柱環梁道數為六道，環梁截面尺寸為500 mm時更接近原模型。與剛度等效公式計算結果對比，確定剛度等效增大系數為1.25。

4 地震作用下結構響應分析

4.1 地震波的選取

本文選取了EL-Centro波、Taft波和人工波SHM2波[19]三種地震波對模型結構進行地震響應分析。根據抗震規范對底部剪力的要求，對選用的地震波峰值數據進行調幅。

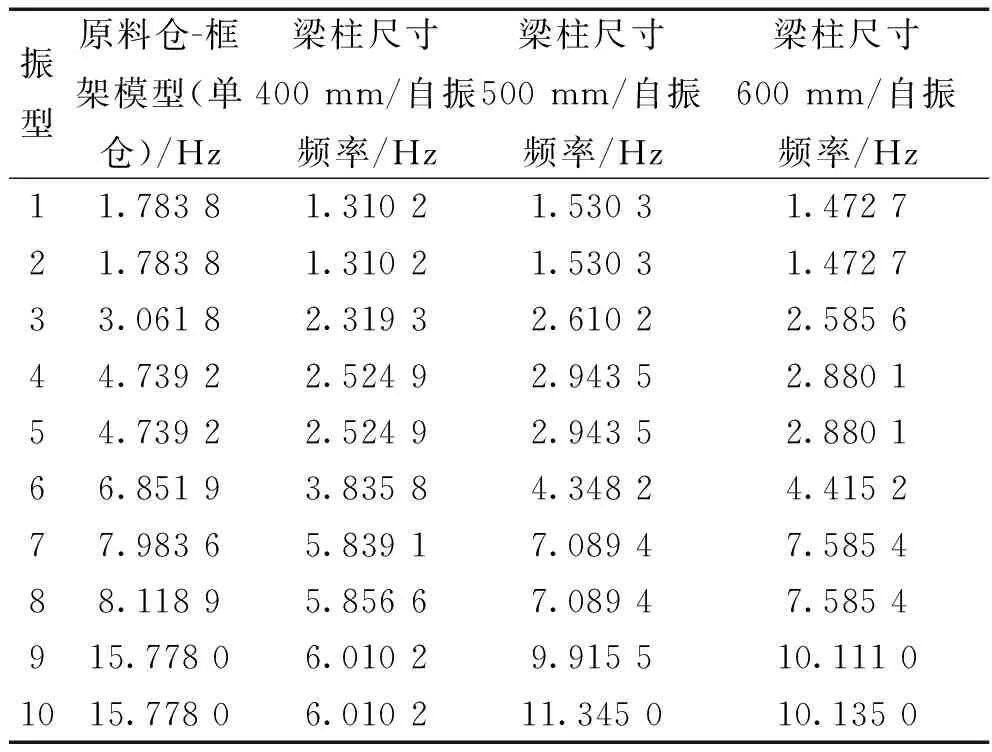
表3 不同尺寸柱-環梁結構的自振頻率

表4 不同道數環梁下結構的自振頻率

4.2 地震波的調整與施加

根據文獻[19]，結合料倉-框架結構基本情況，擬采用地震波參數如下：EL-Centro波，間隔0.02 s，持續時間53.76 s，加速度峰值出現在第2.14 s，峰值為341.7 cm/s2，場地土屬Ⅱ-Ⅲ類，時程曲線和幅值譜曲線如圖5所示；Taft波，間隔0.02 s，持續時間54.40 s，加速度峰值出現在第3.72 s，峰值為175.9 cm/s2，場地土屬Ⅱ類，時程曲線和幅值譜曲線如圖6所示；地震波SHM2，間隔0.02 s，持續時間78.64 s，加速度峰值出現在第13 s，峰值為35 cm/s2，場地土屬Ⅳ類，其時程曲線和幅值譜曲線如圖7所示。

圖5 EL-Centro波Fig.5 EL-Centro wave

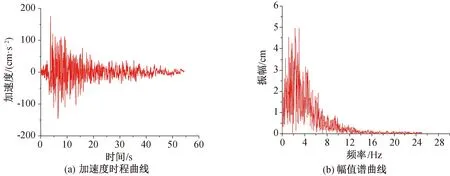
圖6 Taft波Fig.6 Taft wave

圖7 SHM2波Fig.7 SHM2 wave

地震波選取后，根據自己的工況設計，進行地震波的調整，地震波加速度值調整的基本原則是：實際的地震波峰值和時程分析法采用的地震波峰值相等，如式(1)所示，選取料倉-框架結構所在地區設防烈度為7度(設計加速度峰值為0.35 m/s2)。

(1)

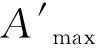
根據抗震設計規范推薦的方法，對加速度地震波的持續時間進行壓縮。一般壓縮的時間為第一次達到該加速度地震波最大峰值的10%時計起，到最后一次達到該加速度地震波最大峰值的10%結束，且壓縮后的時間一般為結構基本周期的5～10倍。本文中輸入的EL-Centro波、Taft波和人工波SHM2波持續時間均為25 s。

4.3 結構位移與應力響應分析

采用時程分析法，輸入調整后的天然波EL-Centro波、Taft波和人工波SHM2波，對柱環梁-框架結構有限元模型進行地震作用下的動力響應分析。在7度多遇水平地震動加速度作用下，得出柱環梁-框架結構位移與應力響應，如圖8所示。

通過分析可知，在EL-Centro波作用下，柱環梁-框架結構最大位移為9.85 mm，出現在柱環梁頂部，柱環梁-框架結構最大等效應力為4.73 MPa，出現在結構柱底；在Taft波作用下，柱環梁-框架結構最大位移為11.67 mm，出現在柱環梁頂部，柱環梁-框架結構最大等效應力為2.64 MPa，出現在結構柱底；在人工波SHM2波作用下，柱環梁-框架結構最大位移為4.35 mm，出現在柱環梁頂部，柱環梁-框架結構最大等效應力為1.28 MPa，出現在結構柱底，表明結構環梁頂部是比較薄弱的部位，位移最大；結構柱底受力最大，應采取積極的保護措施。不同高度下結構的應力位移變化，見圖9所示。

5 結論

1)利用剛度等效原則，計算得出與實際結構剛度等效的柱環梁尺寸為400 mm。通過調整柱環梁尺寸及道數，以獲得和原結構有相同自振特性的模型結構。考慮環梁尺寸影響，分別建立400、500、600 mm不同尺寸的柱環梁-框架結構模型，考慮環梁道數，分別建立四道柱環梁、六道柱環梁和八道柱環梁的柱環梁-框架結構模型，通過與原料倉-框架結構自振特性對比分析，得出柱環梁尺寸為500 mm、柱環梁道數為六道時，模擬結果最為接近原模型。在此基礎上，進而確定剛度等效增大系數為1.25。

2)采用時程分析法，分別考察設防烈度為7度情況，在天然波EL-Centro波、Taft波和人工波SHM2波3種地震波作用下，柱環梁-框架結構地震響應。得到3種工況下，柱環梁-框架結構的最大位移與最大等效應力響應。柱環梁-框架結構最大位移出現在柱環梁頂部，結構受力最大位置出現在柱底，并且位移和應力變化較為均勻，建議實際設計中，應對該部位進行加強處理。

圖8 結構的位移與應力分布圖Fig.8 Structural displacement and stress distribution diagram

圖9 不同高度下結構位移和應力分布圖Fig.9 Structural displacement and stress distribution under different heights