基于代理模型的儲煤倉三心圓柱面屋蓋氣動外形優化研究

李劍鴻，邱 冶，傘冰冰

(河海大學 土木與交通學院，南京 210098)

三心圓柱面屋蓋是大型儲煤倉常見的一種結構形式，具有凈空高、跨度大、經濟性好等優點[1]。隨著我國國民經濟的迅速發展，為滿足存儲和作業空間的需求，大型儲煤倉的高度和跨度日趨增加，風荷載已成為結構設計人員不可忽視的問題。柱面屋蓋是大跨度儲煤倉的主要結構形式。迄今，諸多學者對柱面屋蓋的抗風性能及其影響因素進行了研究。Qiu等[2]通過風洞試驗研究了矢跨比和雷諾數對柱面屋蓋氣動特性的影響，并提出了一種基于改進勢流理論的平均風壓模型。Johnson等[3]對矢跨比為0.27～0.5的柱面屋蓋風荷載特性進行了雷諾數效應研究，發現屋蓋的雷諾數敏感性隨矢跨比的增加而增大。Li和Ding等[4-5]通過剛性模型測壓試驗獲得了矢跨比為1/3和1/5的柱面屋蓋表面的壓力分布，研究發現屋蓋迎風面的壓力隨著矢跨比的增大而顯著減小。基于風洞試驗數據，單魯陽[6]和齊月芹等[7]分別采用0.618法、窮舉法和數學規劃法中的復形法對雙層柱面網殼的矢高、網格尺寸和網殼厚度進行了結構優化分析。三心圓柱面屋蓋的氣動特性與其幾何外形密切相關，但針對這類結構的氣動外形優化研究甚少。本文將基于代理模型和數值模擬技術，對三心圓柱面屋蓋結構進行氣動外形優化研究，以獲得最優的形狀設計參數，為大跨度儲煤倉的抗風設計提供參考。

1 CFD數值模擬

以張雷[8]風洞試驗的三心圓柱面屋蓋作為數值模擬的Benchmark模型，該模型的矢高和跨度分別為H=200 mm、S=540 mm，中間圓弧的半徑為350.6 mm、圓心角為61.32°，兩端圓弧的半徑為187.3 mm、圓心角為54.34°，縮尺比為1∶200。選用標準k-ε、RNGk-ε和SSTk-ω三種湍流模型對柱面屋蓋周圍的繞流流場進行數值模擬，并與風洞試驗數據進行對比驗證。計算域的長度和高度為10 800 mm×2 000 mm，模型位于距來流入口約1/3計算域長度處，圖1為計算域示意圖。采用非結構化網格進行網格劃分，網格總數量約為15萬，屋蓋近壁面處網格尺寸為Δx=S/80、Δz=H/20，其表面y+值約為30～60。圖2為屋蓋附近的網格劃分情況。邊界條件具體設置見表1。

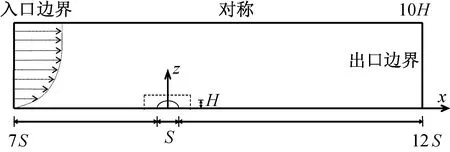
圖1 計算域示意圖Fig.1 Schematic diagram of computational domain

通過數值模擬獲得的屋面平均風壓分布與風洞試驗結果對比如圖3所示。由圖可知，標準k-ε和SSTk-ω湍流模型在屋蓋尾流區的模擬結果與試驗數據偏差較大，而RNGk-ε湍流模型則具有較高的模擬精度，故選用該湍流模型進行三心圓柱面屋蓋的氣動外形優化研究。

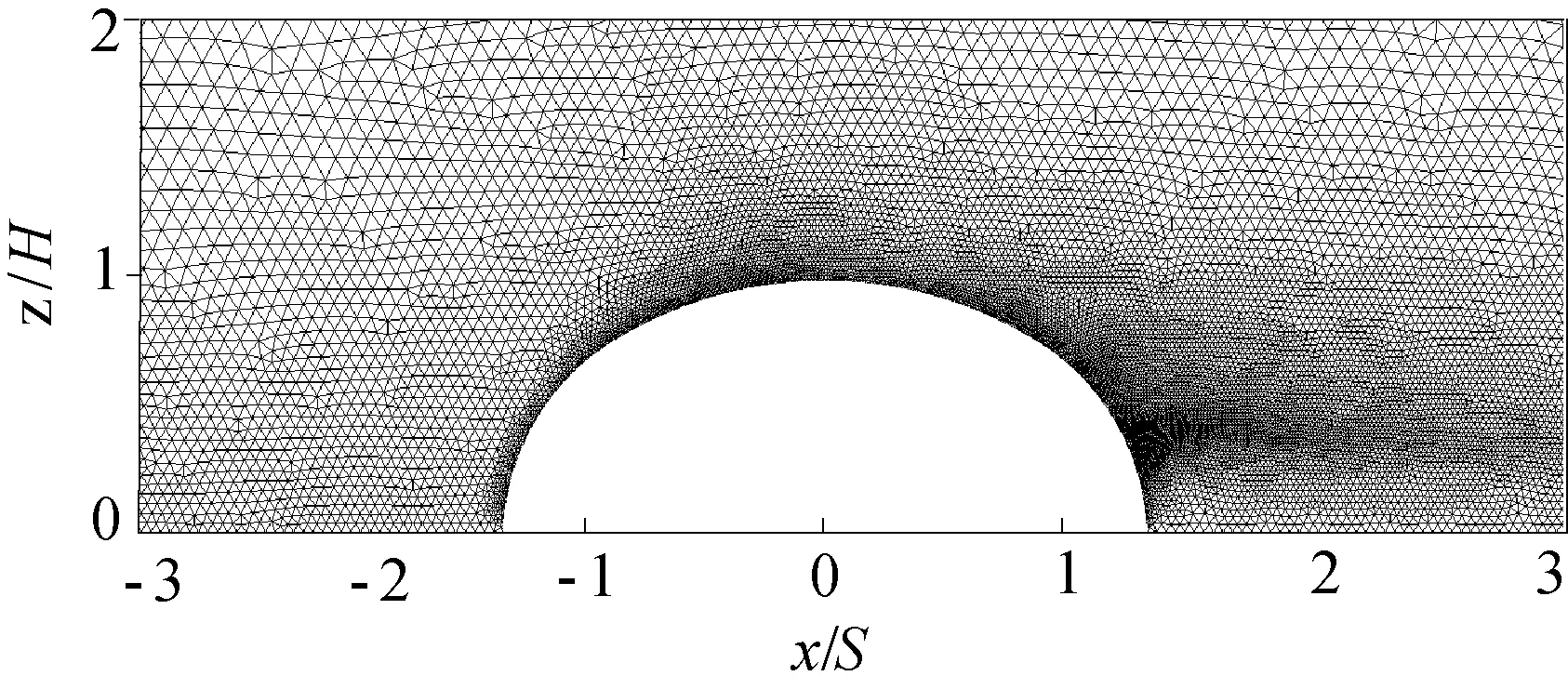
圖2 屋蓋周圍網格劃分Fig.2 Grid system near the roof

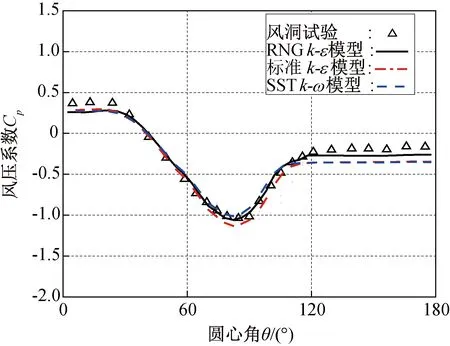
圖3 屋面平均風壓分布的數值模擬與風洞試驗結果對比Fig.3 Comparison of the mean pressure coefficients on the roof surface between numerical simulation and wind tunnel test

2 屋蓋氣動優化模型

圖4為三心圓柱面屋蓋幾何模型示意圖。屋面由半徑為R、圓心角為q的中間圓弧，和半徑為R1、圓心角為q1的兩端圓弧組成。假定中間圓弧與兩端圓弧在其交點處的切線重合，則三心圓柱面屋蓋的幾何參數滿足如下關系式：

(1)

(2)

其中，參數C1和C2可由下式計算得到：

(3)

(4)

表1 計算域邊界條件

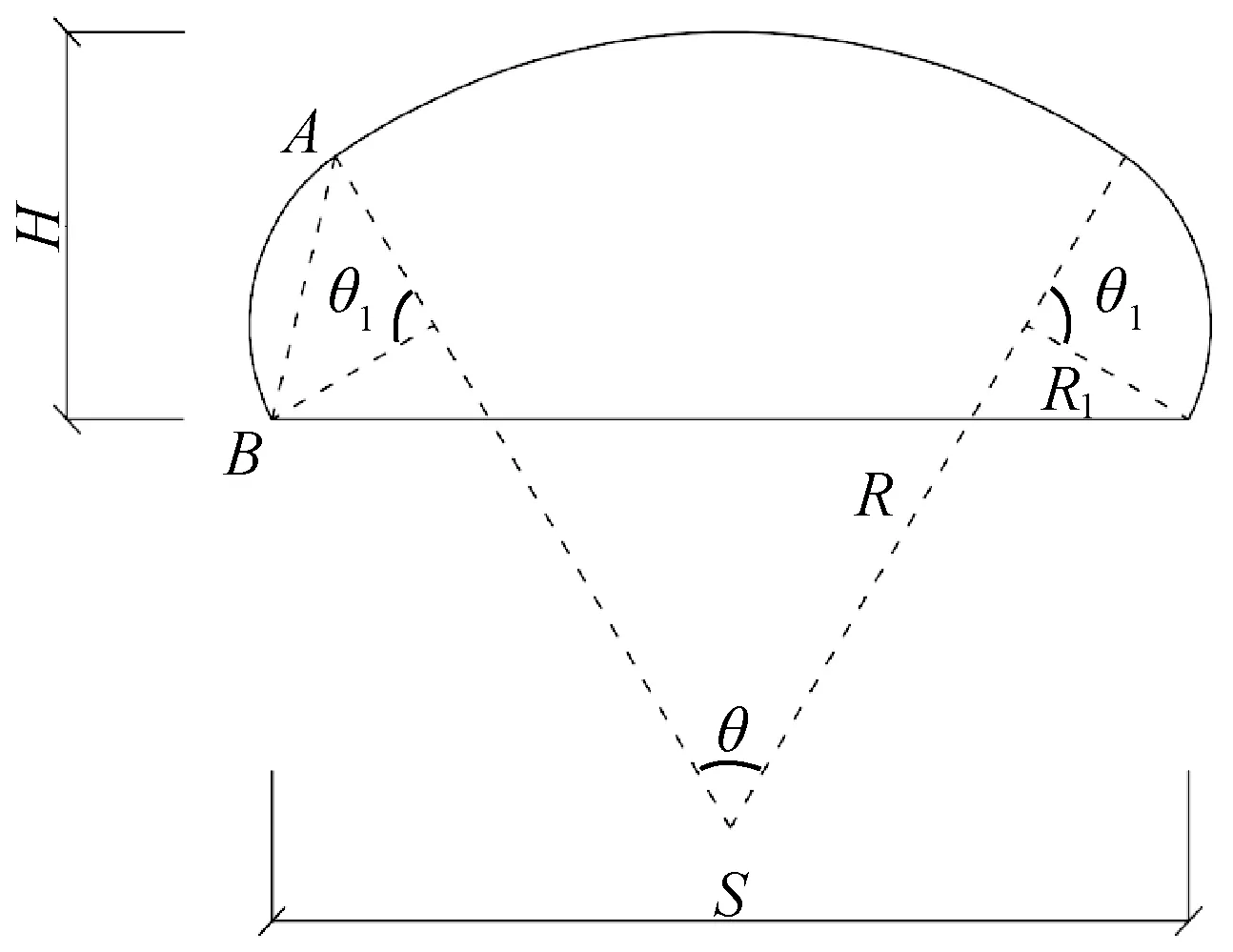
圖4 三心圓柱面屋蓋幾何模型示意圖Fig.4 Schematic diagram of geometry model of the three-centered cylindrical roof

強風作用下柱面屋蓋頂部可能會產生較大的風吸力，致使其發生風致破壞。本文分別以三心圓柱面屋蓋的負壓峰值最小、豎向位移絕對值最小為優化目標，以屋蓋中間圓弧的半徑與跨度之比(R/S)和圓心角(θ)作為優化變量，對其進行氣動外形優化，以獲得最優的形狀設計參數。所以，三心圓柱面屋蓋的氣動外形優化是一個單目標、多變量的優化問題，優化模型表達如下：

minF1(R/S,θ)=max{|Cpi|},

(5)

minF2(R/S,θ)=max{|Wi|},

(6)

式中：F1(R/S，θ)和F2(R/S，θ)為目標函數；Cpi為屋面第i個點的平均風壓系數；Wi為屋面第i個點的豎向位移值。優化變量R/S的上下限分別為lR=0.52和uR=1.48，其中R/S=0.52時，為單心圓柱面屋蓋，而當R/S>1.48時，屋蓋幾何外形變化較小；圓心角θ的上下限分別為lθ=0°和uθ=2arcsin(0.5/(R/S))，其中θ=2arcsin(0.5/(R/S))時，兩側小圓弧起點和終點連線AB垂直于地面。有限元模型采用雙層網殼結構形式，基本參數如下：網殼跨度和高度分別為108、40.26 m，厚度為3.5 m。采用圓鋼管桿件，其長度為4 m，桿件截面尺寸為159 mm×10 mm。

3 優化結果

三心圓柱面屋蓋負壓峰值的預測曲面如圖5所示，由圖可知，目標函數F1與設計變量之間存在著復雜的非線性關系。如圖6所示，研究結果表明，kriging代理模型的預測值與目標函數真實值(CFD模擬)的最大誤差為4%，該代理模型可以構建較為精確的預測曲面。圖5中C1點為最優解，得到R/S=1.26，θ=45.8°，相應的屋面負壓峰值|Cp|max=0.84(位移值|W|=4.665 mm)，與初始形狀相比，屋蓋負壓峰值降低了約17%。圖7為最優解C1對應的屋蓋表面平均風壓分布，與其附近參照點C2 (R/S=1.26，θ=20°)和C3 (R/S=0.93，θ=45.8°)工況的對比圖。由圖可見，優化后的屋蓋頂部風吸力值明顯減小，而尾流區的變化不顯著。

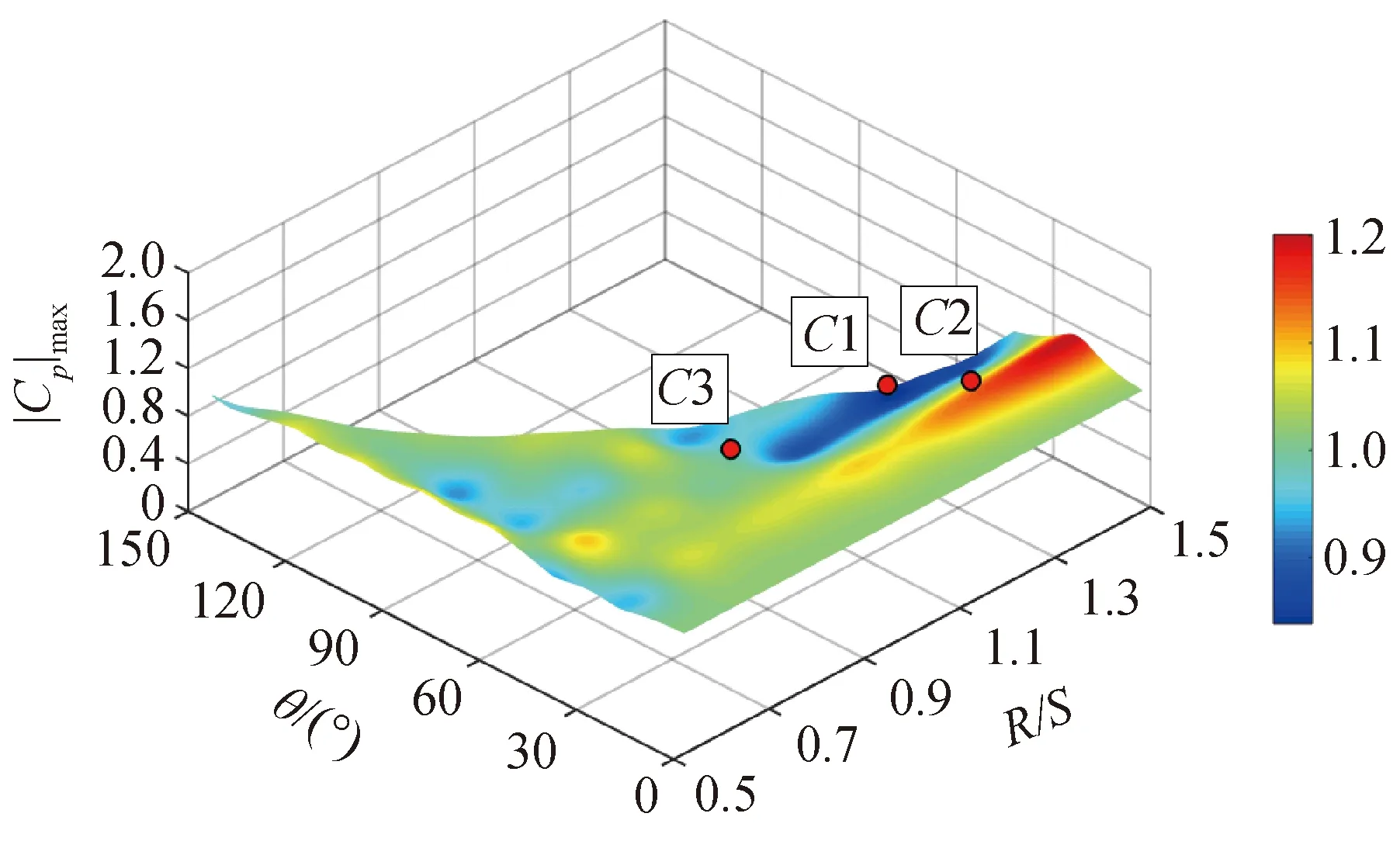
圖5 負壓峰值的kriging模型預測曲面Fig.5 kriging model prediction surface of negative pressure peak

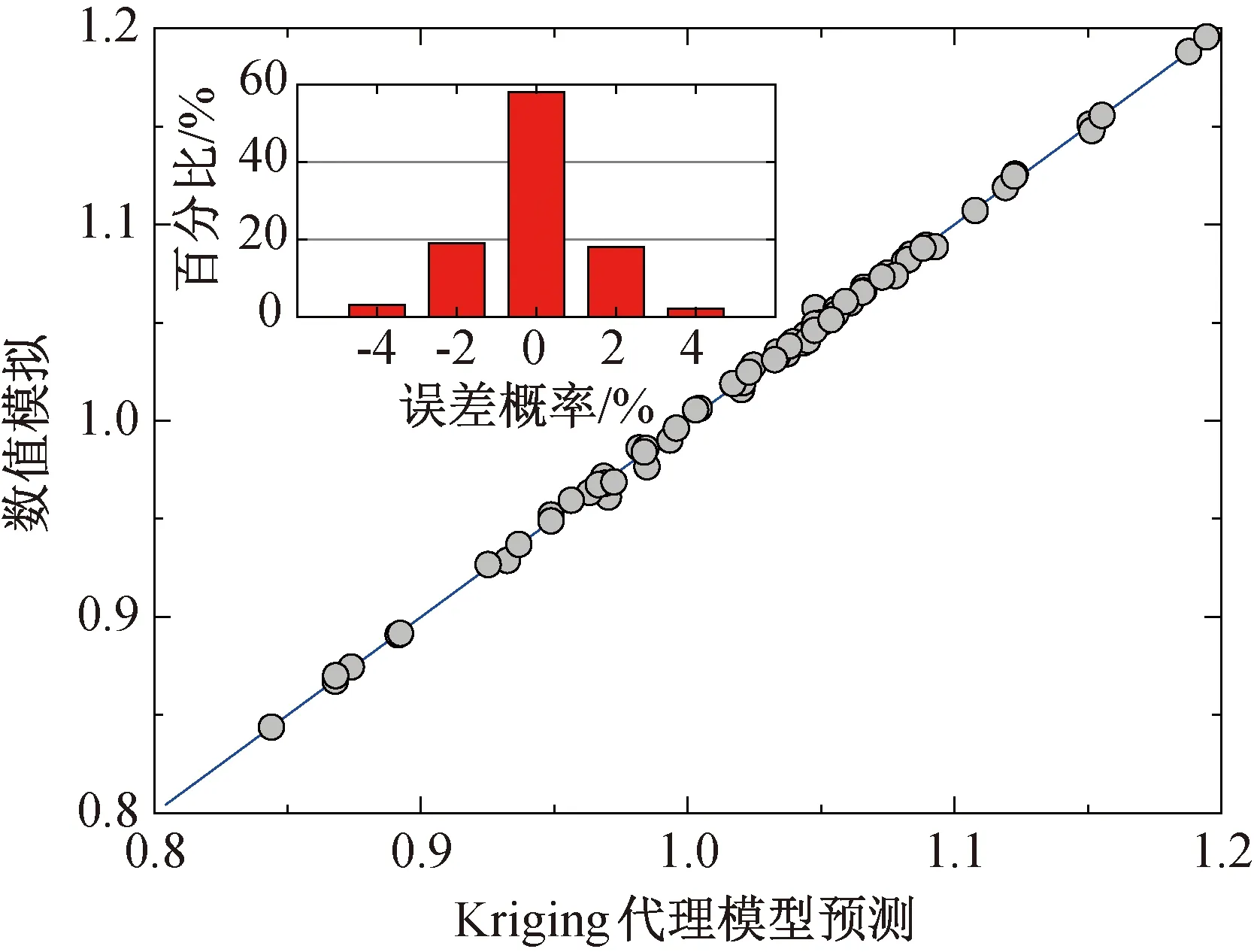
圖6 負壓峰值優化的kriging代理模型的預測值與目標函數真實值的對比圖Fig.6 A comparison diagram of the predicted value of the Kriging agent model optimized by peak of negative pressure and the real value of the objective function

圖8為雙層柱面網殼豎向位移極值的預測曲面。圖中W1點為最優解，得到R/S=0.56，θ=14.1°，相應的網殼豎向位移值|W|max=0.293 mm(負壓絕對值|Cp|=0.95)，與初始形狀相比減小了近55 %。最優解W1與參照點W2(R/S=1.3，θ=20°)和W3(R/S=0.56，θ=120°)對應的屋蓋豎向位移分布如圖9所示，由圖可見位移極值位于網殼頂部區域，具有最優外形的三心圓屋蓋能夠明顯減小其豎向位移極值。

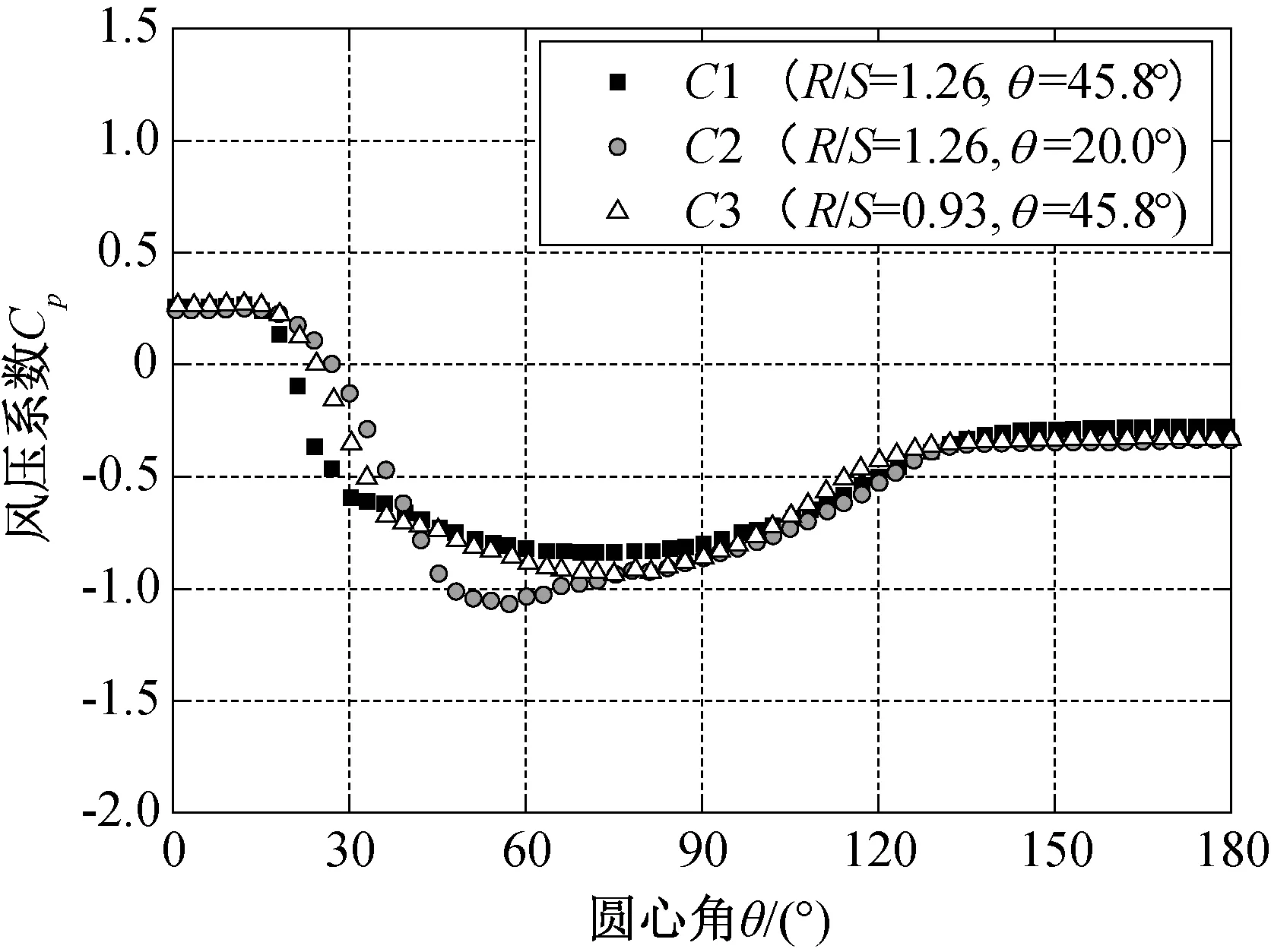
圖7 最優解C1與參照點C2、C3對應的屋蓋表面平均風壓分布圖Fig.7 Mean pressure distributions on the roof surface with optimal (C1) and near optimal (C2 & C3) shapes

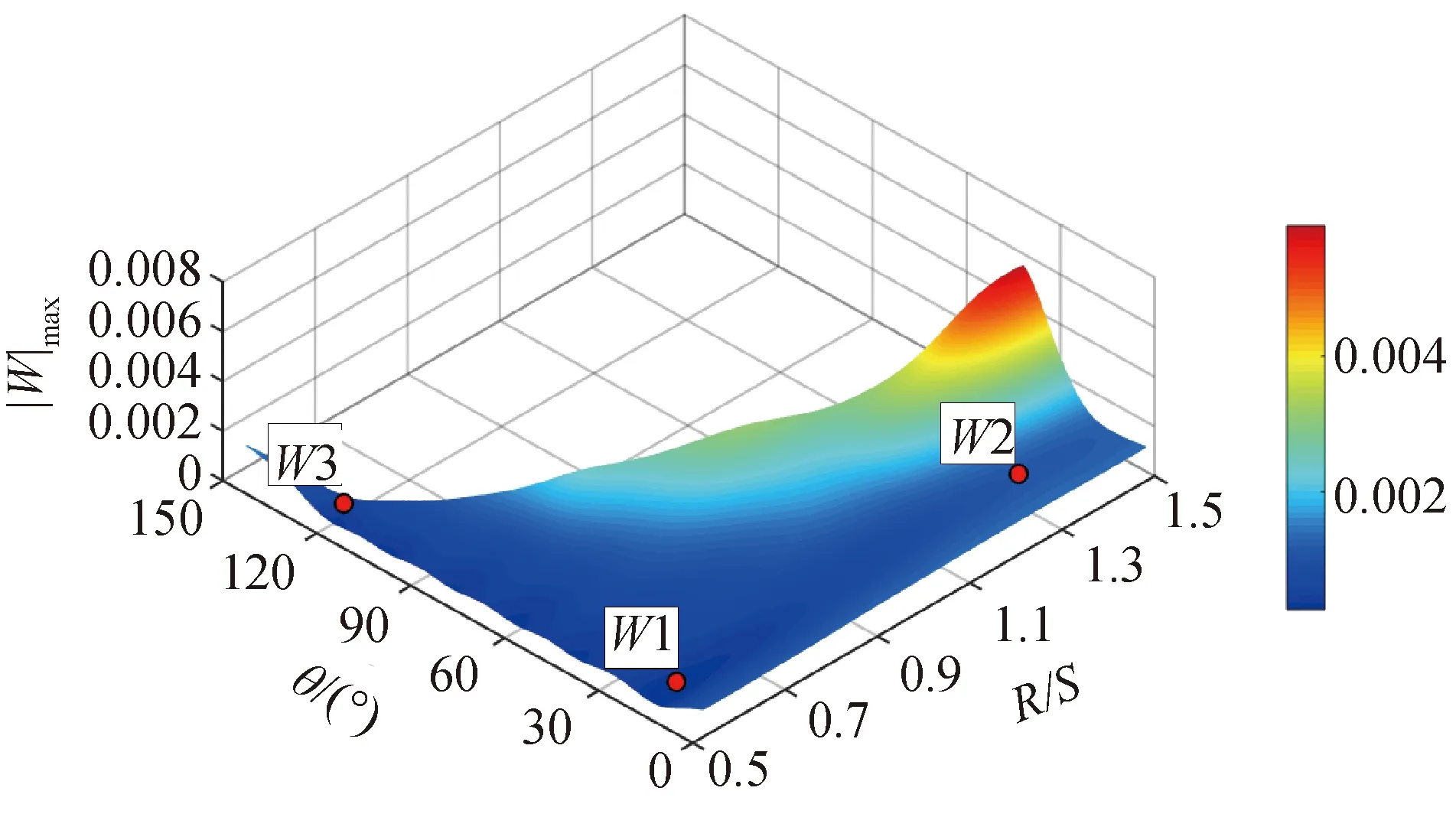
圖8 豎向位移極值的kriging模型預測曲面Fig.8 kriging model prediction surface of vertical displacement extremum

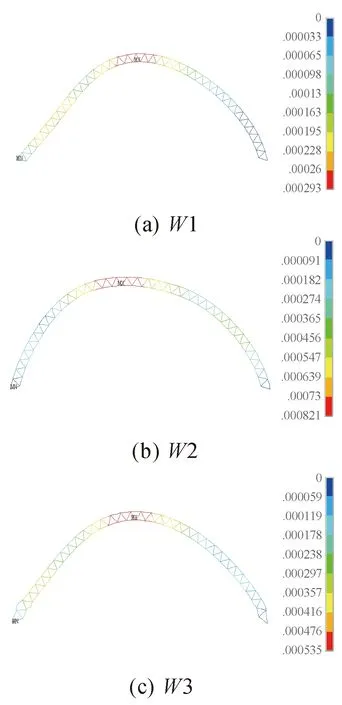
圖9 最優解W1與參照點W2、W3對應的屋蓋豎向位移圖Fig.9 Vertical displacement distributions of roof with optimal solution (W1)and reference points (W2 & W3)

4 結論

1)通過風洞試驗數據對數值模擬算例進行了驗證，研究發現RNGk-ε湍流模型具有較好的模擬精度。

2)基于kriging模型建立了三心圓柱面屋蓋氣動外形優化的代理模型。結果表明，當R/S=1.26，θ=45.8°時，屋面的負壓峰值為|Cp|max=0.84；當R/S=0.56，θ=14.1°時，雙層柱面網殼的豎向位移極值為|W|max=0.293 mm。