孔隙空間分布對粗粒土強度變形特性影響研究

胡有方,袁俊平，盧 毅

(1. 河海大學 巖土力學與堤壩工程教育部重點實驗室，江蘇 南京 210098；2. 河海大學 江蘇省巖土工程技術工程研究中心，江蘇 南京 210098)

粗粒土是一種典型的顆粒材料，由大量粒徑不等、形狀各異、排列隨機的土石顆粒組成，微觀上孔隙結構的多樣性決定了其宏觀物理力學性質的復雜性[1]。因此可以說，粗粒土的變形過程實質上就是其孔隙結構變化的過程，如果能獲得粗粒土的孔隙結構特征和變化規律，也就能掌握其變形規律[2]。近年來，許多國內外學者對粗粒土的孔隙結構特征進行了研究，主要方法有實驗法和數值重構法[3-4]。實驗方法最早起源于1982年，Petrovic等[5]首先在土壤的密度和含水率研究中引入CT掃描技術，之后，Warner[6]則在對CT掃描圖像的分析中發現，孔隙的位置、大小和數量信息都能由圖像精確地揭示。在國內，學者呂菲[7]等在掃描圖像的基礎上建立了孔隙網絡模型，并成功預測了飽和土壤的水力學性質。相方園[8]使用切片法進行試驗，將孔隙拓撲結構與形態學理論相結合，定量地獲得了孔隙結構中的特征參數。與實驗方法不同，數值重構法的思路是基于二維孔隙信息和不同的數學模擬算法建立三維孔隙結構模型，目前常用的方法有高斯隨機場法[9]、過程法[10]和模擬退火法[11]。比較成功的案例有Pilotti[12]基于過程法，用一種主要適用于球體、橢球體、圓柱體和平行六面體的算法建立了任意形狀顆粒的隨機堆積體。曾建邦[13]等利用改進的模擬退火法重建了含水沉積物的三維孔隙結構，并通過孔隙結構的特征化分析揭示了分布模式對沉積物特性的影響。

綜上所述，目前的研究主要針對的是粗粒土孔隙結構特征的描述方法，因此，如何將粗粒土的孔隙結構特征與強度變形特性定量地聯系起來，仍是有待探討的問題。本文在前人的研究基礎上，從孔隙空間分布的不均勻性出發進行研究，定義了可以定量刻畫粗粒土孔隙空間變異性的孔隙空間分布系數FSD；基于PFC3D離散元軟件，分析了FSD與粗粒土強度變形參數之間的關系；同時，基于Abaqus有限元軟件，分析了FSD在有限元計算中的適用性。

1 土體孔隙空間分布不均勻性的定量刻畫

首先，粗粒土試樣中各巖土顆粒和孔隙的位置可以通過掃描的方法得到[14]。接下來，使用最大球算法[15]對孔隙進行模擬，即對于每一部分孔隙，插入若干個以巖土顆粒為邊界的最大內切球，使這些球充滿孔隙空間。以各球體的質心作為孔隙的質心，以各球體的體積作為孔隙的體積，從而達到以大量規則的球體模擬不規則的孔隙體的目的，最大球算法的示意圖如圖1所示。

圖1 最大球算法示意圖Fig.1 Schematic diagram of maximum sphere algorithm

下一步，將土體劃分為N個相同的區域對孔隙球體進行統計，由于粗粒土的不均勻性，每個區域內的孔隙數量和孔隙體積分布都不相同，因此引入孔隙數量變異系數CVn和孔隙體積變異系數CVv，兩者的表達式分別為

(1)

(2)

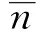
CVn和CVv可以較好地將試樣中孔隙數量的分布情況和孔隙體的分布情況反映出來，其值越小，則代表均勻性越好。理想情況下，孔隙分布完全均勻時，兩者值為0。但要注意的是，這兩個參數本身無法反映出孔隙質心點在空間中的分布情況，因為存在偏聚現象，如圖2所示，a試樣與b試樣的CVn和CVv相同，但顯然a試樣的偏聚程度小于b試樣。因此，還需要引入偏聚系數β來反映這種情況。

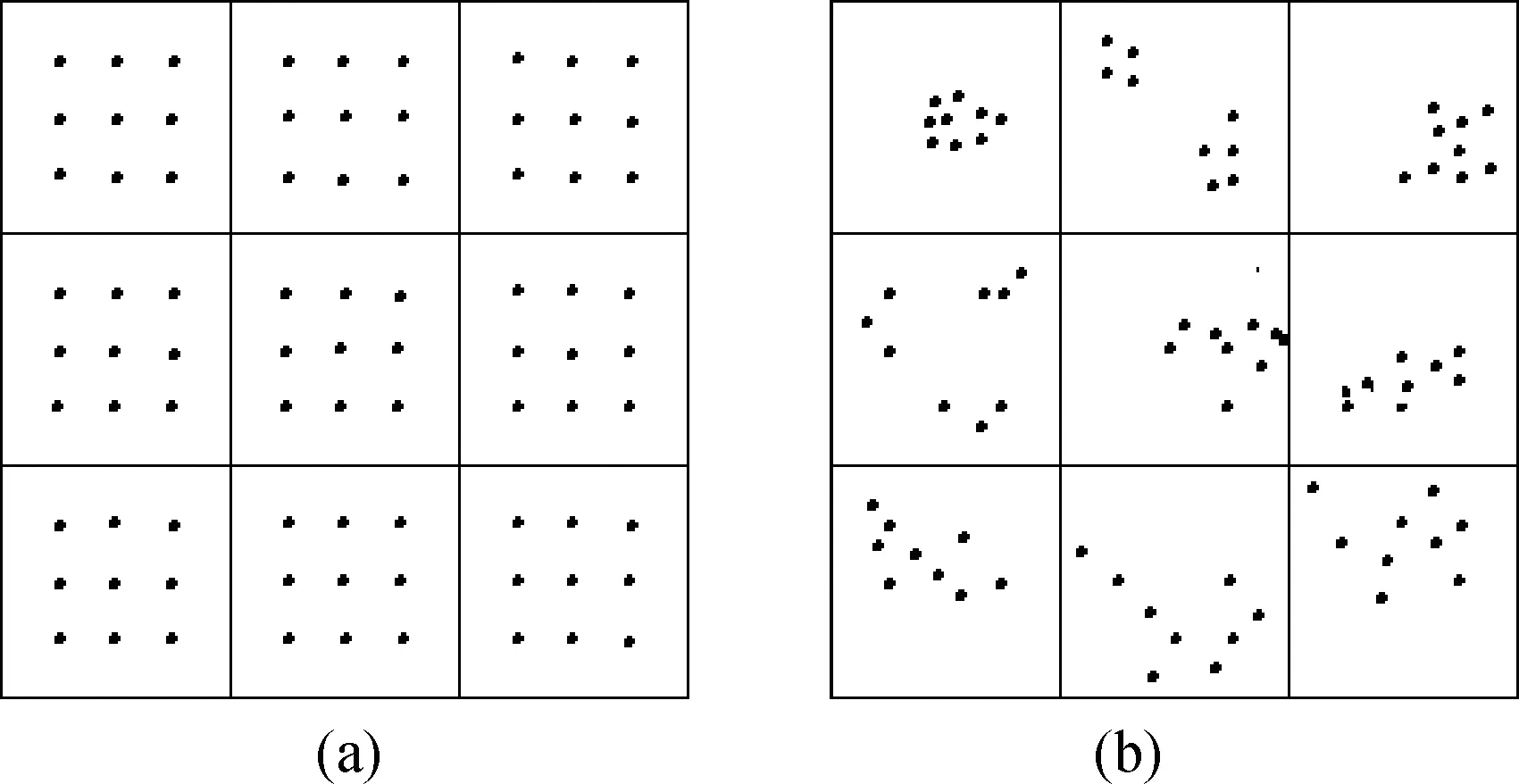
圖2 孔隙空間分布狀態示意圖Fig.2 Diagram of pore space distribution

(3)

式中：n表示樣本區域內孔隙總數量。

接著，用x0表示試樣中孔隙完全規則地分布在試樣空間中時孔隙之間的距離，然而對于任意的n值，x0的值都難以計算，因此本文用下式代替：

(4)

式中：v表示樣本區域內孔隙總體積。如此計算時，x0表示當n個相同尺寸的球體孔隙總體積與樣本區域內孔隙總體積相等時這些孔隙的直徑。

于是，偏聚系數β可以用下式計算：

(5)

在得到了孔隙數量變異系數CVn，孔隙體積變異系數CVv以及偏聚系數β之后，本文定義孔隙空間分布系數FSD作為綜合性指標，從孔隙質心點空間分布的均勻性、孔隙體積空間分布的均勻性以及孔隙質心在空間上的偏聚程度三個方面綜合反映孔隙空間的分布情況，其表達式定義為

FSD=β·CVn·CVv

(6)

2 孔隙空間變異系數與土體強度變形參數關系研究

在定義了孔隙空間分布系數FSD之后，為了研究其對土體宏觀強度變形特性的具體影響，就需要定量分析FSD與土體各項強度參數之間的關系。因此本節中基于PFC3D軟件，建立了5組三軸壓縮試驗試樣進行數值模擬實驗。試樣編號為PK1—PK5，高度H=200 mm，直徑D=101 mm。這些試樣的總孔隙率相同，但各試樣的內部分層情況不同，詳細參數和示意圖如圖3所示。

試樣模型按照以下步驟建立：(1)將試樣空間按照試驗方案均分為指定層數，從最底層開始生成顆粒；(2)使用半徑擴大法生成試驗方案中指定孔隙率的土顆粒，在每層頂部多預留5 cm的高度；(3)賦予土顆粒重力加速度，使土顆粒在重力作用下自由下落形成堆積體；(4)賦予該層頂部墻體一定速度使其下落直至獲得該層指定尺寸的試樣，運行一定時步使試樣達到穩定狀態，該層試樣生成完畢；(5)重復(2)—(4)步驟直至所有層的試樣均生成完畢，刪除中間墻體，運行一定時步使試樣達到穩定狀態，試樣生成完畢。模型生成過程如圖4所示。

完成試樣的生成后，為了防止偶然誤差給數值試驗結果帶來影響，對各試樣進行多次對照試驗，結果取平均值。最終統計各試樣的孔隙空間分布系數FSD如表1所示。

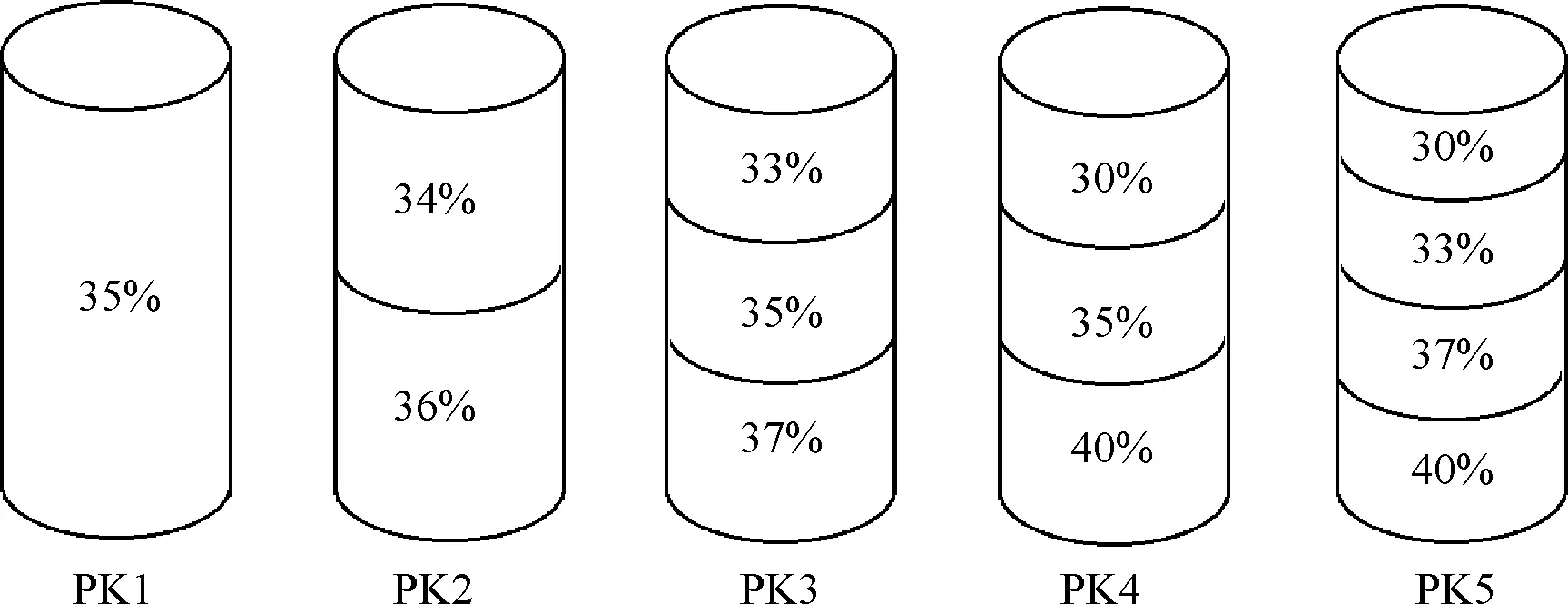
注：數據為各層孔隙率。圖3 不同孔隙空間分布影響效應試驗方案示意圖Fig.3 Schematic diagram of test scheme for effect of different pore space distribution

圖4 模型生成過程示意圖Fig.4 Diagram of model generation process

從表1可以看出，在其他顆粒細觀參數相同的條件下，各試樣的孔隙空間分布系數因分層的不同而發生了明顯的變化。試樣PK5相對于試樣PK1，空間分布系數FSD增大了46.8%，說明該方法的合理性。

為了得到上述各試樣的應力和應變曲線，對表中的各組試樣進行圍壓800 kPa的三軸固結排水試驗數值模擬，結果如圖5和圖6所示。

從圖5和圖6中可以看出，在其他顆粒細觀參數相同的條件下，土體的彈性模量、峰值強度和泊松比都隨著孔隙空間分布系數FSD的增大而減小。試樣PK5相對于試樣PK1，彈性模量減小40.8%，峰值強度降低12.5%，泊松比減小39.5%。

表1 各試樣孔隙空間分布系數

圖5 偏應力-軸向應變曲線Fig.5 Relationship between deviatoric stress and axial strain

圖6 側向應變-軸向應變曲線Fig.6 Relationship between lateral strain and axial strain

由于加載剛進行時，試樣的偏應力-軸向應變曲線近似為一條直線，因此將試樣軸向應變達到1%時的割線模量作為試樣的彈性模量。相關性分析結果表明，彈性模量E與孔隙空間分布系數FSD之間呈指數函數關系，如式(7)。

E=A1+B1er1FSD

(7)

用指數函數對試樣彈性模量E和孔隙空間分布系數FSD進行擬合，結果如圖7所示，其中A1的值為94.062 2，B1的值為-0.609 4，r1的值為-2 071.968 1。

將軸向應變1%時的切線泊松比作為試樣的泊松比，相關性分析結果表明，泊松比ν與孔隙空間分布系數FSD呈指數函數關系，如式(8)。

v=A2+B2er2FSD

(8)

圖7 彈性模量隨空間分布系數變化曲線Fig.7 Relationship between elastic modulus and pore space distribution coefficient

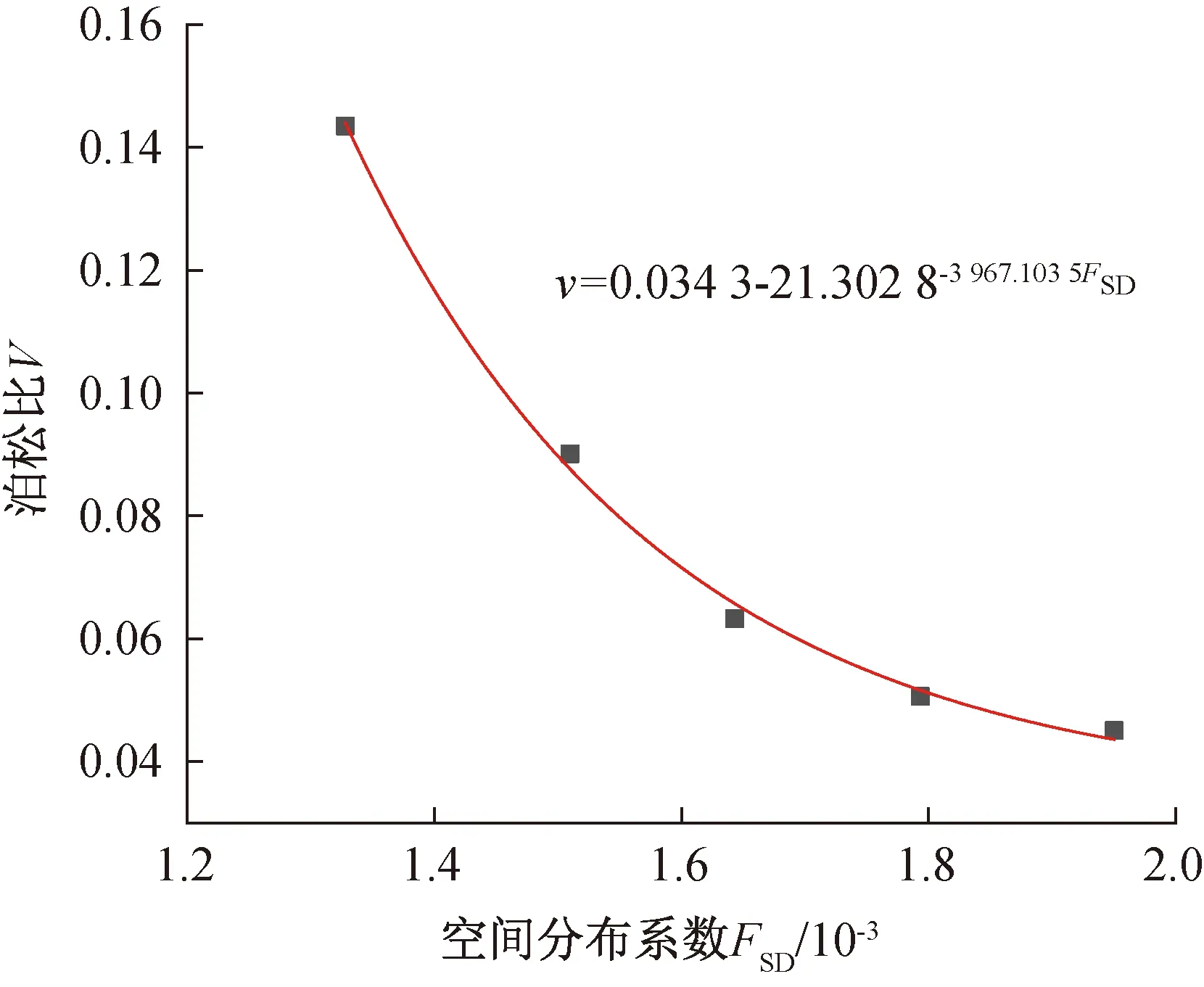
圖8 泊松比隨空間分布系數變化曲線Fig.8 Relationship between Poisson′s ratio and pore space distribution coefficient

用指數函數對二者進行擬合，結果如圖8所示，其中A2的值為0.034 3，B2的值為-21.302 8，r2的值為-3 967.103 5。

為了得到各試樣的內摩擦角，在圍壓200、800和2 000 kPa的條件下，對各試樣進行三軸試驗數值模擬，得到了各試樣在不同圍壓下的峰值強度。根據莫爾-庫倫強度理論，各試樣的內摩擦角如表2所示。

表2 各試樣內摩擦角

為了研究試樣內摩擦角與孔隙空間分布系數之間的定量關系，對內摩擦角與孔隙空間分布系數進行相關性分析，發現兩者之間呈指數函數關系，如式(9)。

φ=A3+B3er3FSD

(9)

用指數函數對試樣內摩擦角和空間分布系數進行擬合，結果如圖9所示，其中A3的值為38.469 2，B3的值為-0.156 7，r3的值為1 705.456 1。

3 孔隙空間分布系數的準確性驗證與分析

本節中使用Abaqus有限元軟件對孔隙空間分布系數FSD計算方法的準確性進行驗證。相比于離散元方法，有限元方法更適合大規模的工程計算，這是由于有限元將粗粒土復雜的幾何結構簡化為了具有簡單形狀的單元，單元內的材料性質和控制方程通過單元節點的未知量來進行表達，從而使得計算的效率大大提高，然而這也使得有限元計算時忽略或低估了孔隙空間分布系數FSD的影響。那么孔隙空間分布系數FSD是否可以被忽略，是否可以使用Abaqus有限元軟件進行孔隙空間變異性的模擬，這是本節中要討論的問題。

為了解決此問題，建立編號分別為A1—A5的5種三軸固結排水實驗試樣，試樣的高度、直徑均與PK1—PK5相同。同時，通過上節中的結果推算出試樣的彈性模量、泊松比、內摩擦角，使得兩組試樣的等效強度參數全部相同，具體數值如表3所示。最后，設置試樣的孔隙率均為35%，使其為均勻試樣。

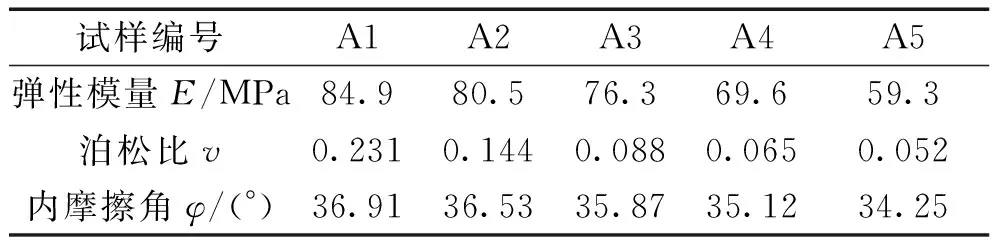
表3 A1—A5試樣強度參數

對試樣施加800 kPa的圍壓時，各試樣的偏應力-軸向應變曲線如圖10所示。

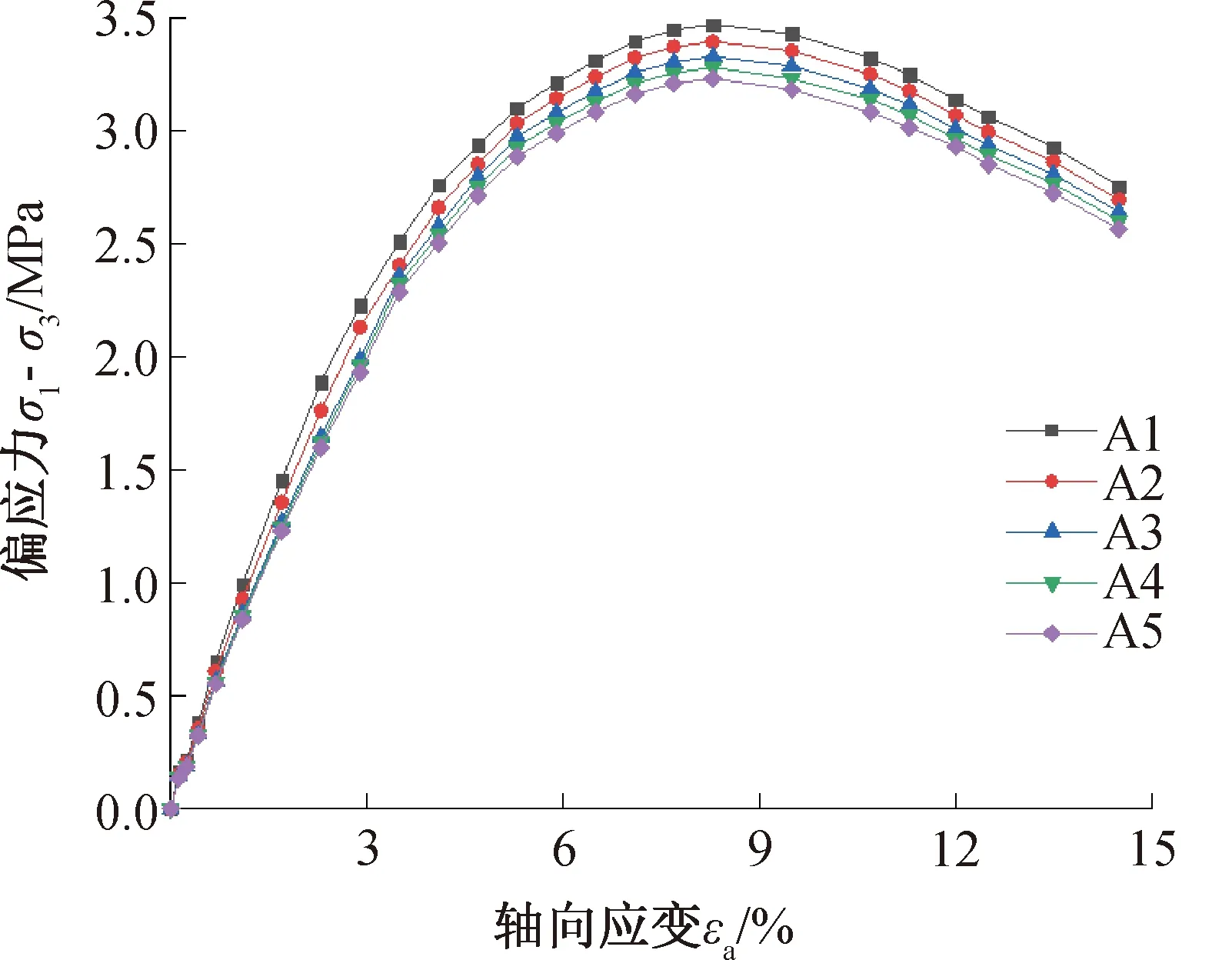
圖10 試樣A1—A5偏應力-軸向應變曲線Fig.10 Relationship between deviatoric stress and axial strain of sample A1—A5

從圖10中可以看出，由于試樣A1—A5忽略了孔隙空間分布系數FSD，消除了空間分布差異對強度的不利影響，使得雖然試樣的各項強度參數均與離散元計算時相同，但試樣破壞時的偏應力均偏大，并且隨著離散元試樣中FSD的增加，這種差異更加明顯。試樣A1相比試樣PK1，破壞時的偏應力增大了1.6%，試樣A5相比試樣PK5，破壞時的偏應力增大了12.0%。

為了降低有限元單元的均勻性，增加孔隙空間分布系數的影響，采用上節圖3中的分層方法建立5種三軸固結排水實驗試樣B1—B5，在前者的基礎上額外考慮不同土層孔隙率的差異。同樣對試樣施加800 kPa的圍壓時，各試樣的偏應力-軸向應變曲線如圖11所示。以試樣5為例，將三次試驗的結果進行比較，如圖12所示。

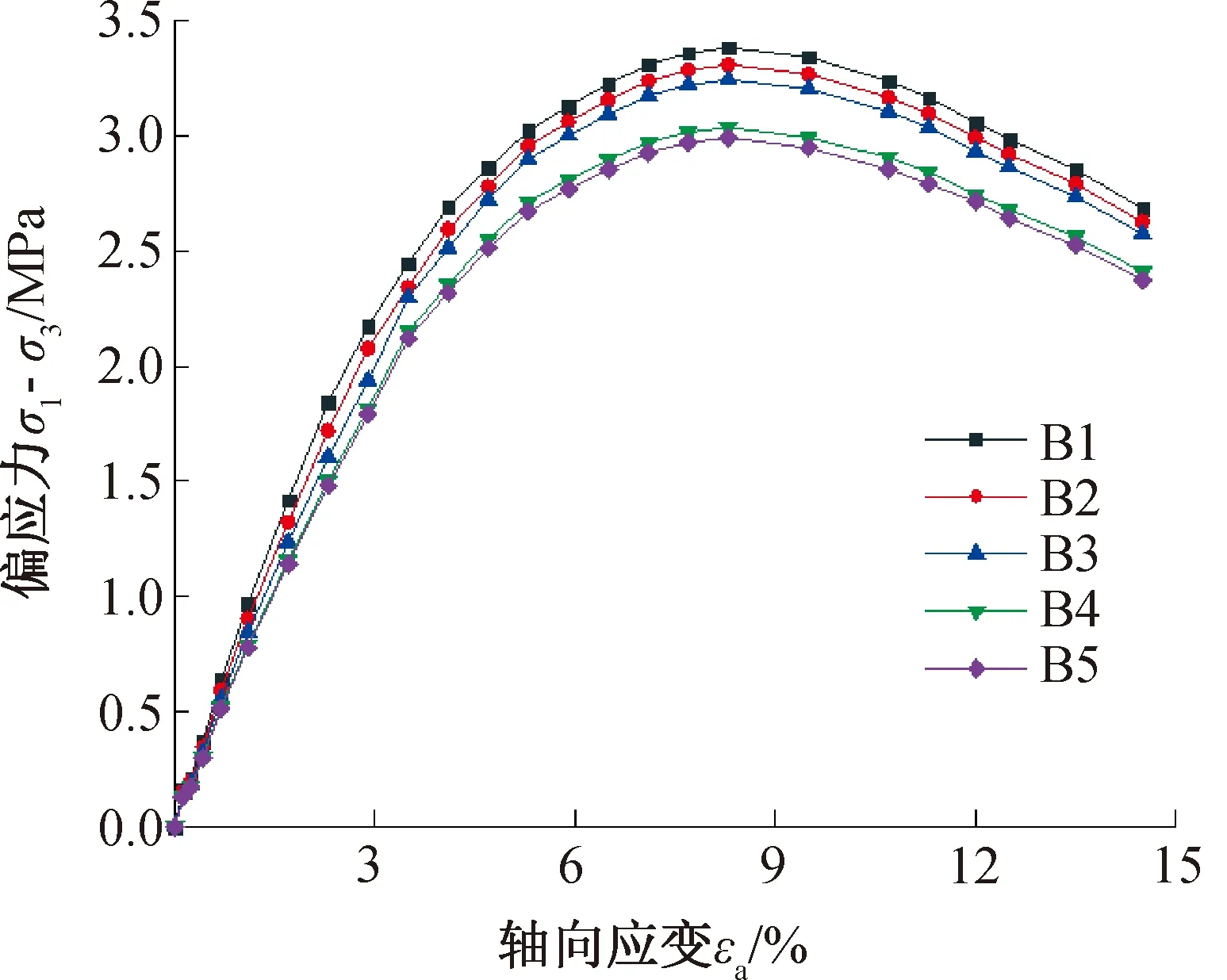
圖11 試樣B1—B5偏應力-軸向應變曲線Fig.11 Relationship between deviatoric stress and axial strain of sample B1—B5

圖12 試樣A5,B5,PK5偏應力-軸向應變曲線Fig.12 Relationship between deviatoric stress and axial strain of sample A5,B5,PK5

從圖11中可以看出，對于考慮分層的有限元試樣，其峰值強度相比均勻的有限元試樣有所降低，但仍然比離散元試樣大。這是因為，雖然分層增加了層與層之間的孔隙空間分布差異，但單獨每個層內的孔隙仍然是均勻的，其FSD雖然大于0，但仍小于離散元試樣。

從圖12中可以看出，對試樣5來說，雖然三次試驗的等效強度完全相同，但三次試驗的峰值偏應力分別為2.74，3.07，2.99 MPa。再次驗證了試樣的峰值強度隨著孔隙空間分布系數FSD的增大而減小的規律，并進一步論證了孔隙空間分布系數FSD計算方法的合理性。同時也說明，在試樣離散型較大時，不應當忽略孔隙空間分布變異性的影響。

4 結論

1)孔隙空間分布系數FSD可以較好地模擬粗粒土中孔隙空間分布的不均勻性。這種不均勻性包括孔隙質心點空間分布的不均勻性、孔隙體積空間分布的不均勻性以及孔隙質心在空間上不同的偏聚程度，因此FSD是一項比較系統的綜合性指標。

2)孔隙空間分布系數FSD在離散元和有限元分析中均能得到較好的運用。在其他顆粒細觀參數相同的條件下，土體的彈性模量、峰值強度和泊松比都隨著孔隙空間分布系數FSD的增大呈指數函數形式減小。