BDS-3/BDS-2多頻偽距單點定位模型研究

魏盛桃，張 建，李得海，秘金鐘，吳文壇

(1.山東科技大學測繪與空間信息學院，山東 青島 266590；2.中國測繪科學研究院，北京 100830；3.中國礦業大學(北京)，北京 100083；4.河北省自然資源檔案館，河北 石家莊 050000)

0 引言

我國在2020年6月23日發射了北斗三號最后一顆全球組網衛星，宣告北斗三號系統(簡稱BDS-3)全面建成。偽距單點定位因為其定位速度快且無整周模糊度問題，在導航定位中應用極為廣泛，相關算法研究也已十分成熟[1]。目前與北斗系統相關的研究主要以精密軌道與鐘差等研究領域為主[2-5]。卻對BDS-3/BDS-2多頻單點定位技術研究較少。張乾坤等[1]利用實測數據，以BDS-3多個頻點聯合BDS-2、Galileo進行同頻組合定位，并對其定位性能進行了研究。肖青懷等[6]驗證了多普勒平滑偽距理論在基于Android平臺的偽距單點定位上實現的可能性。李金華等[7]對多個系統之間的組合在不同截止高度角下的偽距單點定位性能進行了比較分析，研究結果表明，四系統組合在全天歷元可用和實現偽距單點定位前提下，整體定位性能優于其他模式。李衛軍等[8]基于基于IGS連續跟蹤站多模實測 GNSS 數據，分析了單系統以及不同組合系統下的偽距單點定位精度。方欣頎[9]等在全球范圍對BDS-2、BDS-3單系統以及BDS-2/BDS-3組合偽距單點定位精度進行了分析,并評估了BDS-2/BDS-3組合對BDS-2單系統偽距單點定位精度邊緣效應的改善程度。

利用MGEX多站觀測數據，并結合抗差理論對BDS-3/BDS-2單、雙、多頻偽距模型定位性能展開研究，并對每個模型的優缺點進行了分析與討論，對研究多頻偽距單點定位的學者起到借鑒作用。

1 偽距單點定位原理

1.1 單頻偽距單點定位原理

BDS單頻偽距觀測方程可寫成:

(1)

V=A·Δx-L，

(2)

(3)

式中，l，m，n表示接收機到衛星的方向余弦；s為衛星個數。

根據最小二乘求得改正數：

Δx=(ATPA)-1ATPL

，

(4)

式中，P為觀測值權陣。最后得到接收機的坐標為：

(5)

式中，(X，Y，Z)表示接收機的三維坐標；(X0，Y0，Z0)表示接收機的改正前得到的三維坐標。

1.2 多頻偽距單點定位原理

北斗雙頻定位相對于單頻定位的不同之處，主要是利用無電離層組合消除電離層誤差影響，而單頻是利用電離層模型計算電離層誤差[13]。

無電離層組合偽距為：

(6)

無電離層組合偽距觀測方程為：

PIF=ρs-c×Vtr+c×Vts-Vtrop-εi

，

(7)

式中，PIF表示無電離層組合偽距觀測值；i是頻點種類；s為衛星序號；c為光速；Vts，Vtr分別為衛星鐘差與接收機鐘差；Vtrop為對流層延遲；ρs為站星距；εi為觀測誤差。

北斗三頻定位與雙頻定位不同，三頻消電離層組合模型僅構造一個三頻線性組合，與雙頻無電離層組合類似，可根據無電離層影響，幾何距離不變以及最小噪聲求解組合系數[14]。由于該模型只有一組偽距。偽距可被接收機鐘差吸收。因此，三頻消電離層組合的偽距觀測方程為：

Pr，123=ρs-c×Vtr+c×Vts,123-Vtrop-εi，

(8)

Vts,123=Vts+e1br,1+e2br,2+e3br,3，

(9)

式中，Pr，123表示無電離層組合偽距觀測值；i為頻點種類；s為衛星序號；c為光速；Vtr為衛星鐘差；Vts,123為三頻組合的接收機鐘差；Vtrop為對流層延遲；ρs為站星距；εi為觀測誤差。e1,e2和e3為三頻消電離層的組合系數；br,i(i=1,2,3)分別表示第i個頻率的接收機延遲。

1.3 抗差處理

首先應基于觀測值的驗后殘差，對觀測值進行排序，剔除殘差絕對值超過3倍中誤差對應的觀測值，只剔除其中的最大項。

對標準化殘差次最大值對應的觀測值利用IGGⅢ定權模型進行加權處理。對于IGGⅢ權函數，其權因子為：

(10)

(11)

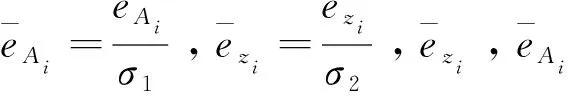
基于上述理論進行迭代求參，直到前后兩次參數之差滿足閾值要求后，停止迭代。

2 實驗分析

為論證分析BDS-3/BDS-2多頻偽距單點定位模型研究,采用MGEX站24h的30 s采樣間隔的觀測數據進行下述實驗。

基于SGOC測站數據，以ENU方向定位偏差與可用衛星數及PDOP值作為性能評價指標，初步分析BDS-3/BDS-2單頻SPP定位性能。同時為增強文章結論的普適性對多測站BDS-3/BDS-2單頻SPP在ENU方向上的RMS進行統計分析。

為論證分析BDS-3/BDS-2單、雙、三頻SPP定位性能，基于SGOC測站數據，對3種模式下BDS-3/BDS-2SPP定位殘差進行對比分析；同時統計各測站平均RMS。

2.1 BDS-3/BDS-2單點定位性能分析

為論證分析BDS-3/BDS-2單點定位性能，以SGOC測站為例，基于單頻定位模型對定位殘差進行統計分析，如圖1所示。由圖1可以看出，BDS-3/BDS-2單頻SPP其平面精度可控制在2 m以內；高程方向精度可控制在 6 m以內。

為進一步分析BDS-3/BDS-2的可用性與可靠性，對各歷元可用衛星數與PDOP值進行統計分析，由圖2可知，基于BDS-3/BDS-2聯合單點定位其PDOP值穩定，定位結果可靠性強同時衛星可見數充足利于進行數據抗差處理。

為增強文章結論的普適性對多測站BDS-3/BDS-2單頻SPP在ENU方向上的RMS進行統計分析，如圖3所示，BDS-3/BDS-2單頻單點定位在各個測站ENU方向定位性能表現大致相同。BDS-3/BDS-2單頻SPP E方向平均RMS在0.7 m以內；N方向平均RMS在0.9 m以內；U方向平均RMS在4.5 m以內。

圖1 SGOC測站單頻SPP定位殘差Fig.1 Positioning residual of single-frequency SPP at SGOC station

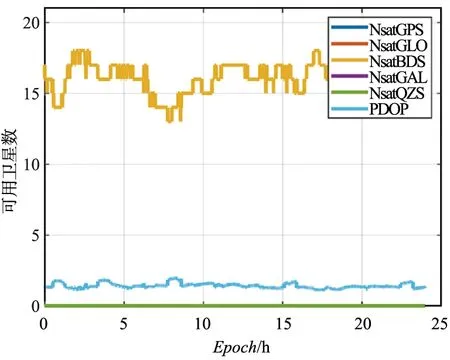
圖2 SGOC測站各歷元可用衛星數與PDOP值Fig.2 Available satellite number and PDOP value of each epoch at SGOC station

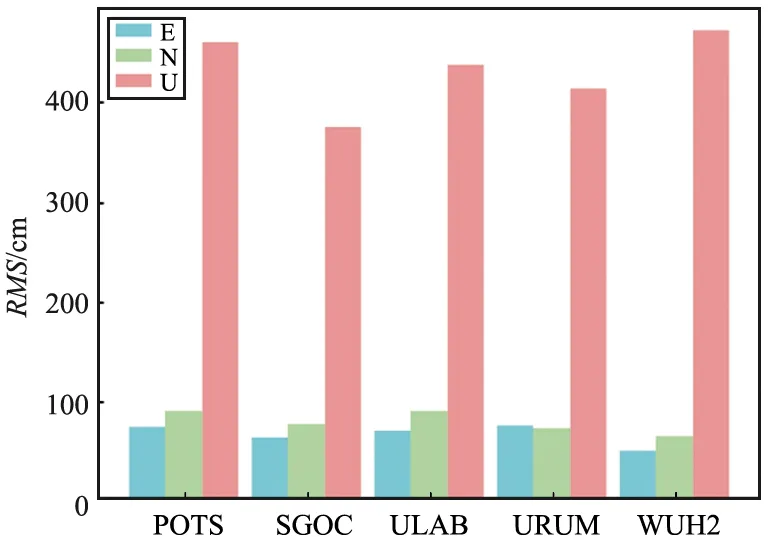
圖3 多測站BDS-3/BDS-2單頻SPP平均RMSFig.3 Mean RMS of BDS-3/BDS-2 single-frequency SPP at multiple stations

2.2 BDS-3/BDS-2偽距定位模型性能分析

針對目前BDS-3/BDS-2提供多頻觀測值，對BDS-3/BDS-2單、雙、三頻偽距單點定位模型性能進行分析，基于SGOC測站數據，對3種模式下BDS-3/BDS-2SPP定位殘差進行對比分析。單頻SPP定位殘差如圖4所示，雙頻SPP定位殘差如圖5所示。由圖5可以看出，BDS-3/BDS-2雙頻偽距單點定位殘差U方向沒有零偏影響，由于雙頻偽距單點定位模型利用無電離層組合消除電離層誤差，有效抵抗電離層誤差影響，提高了U方向定位精度。

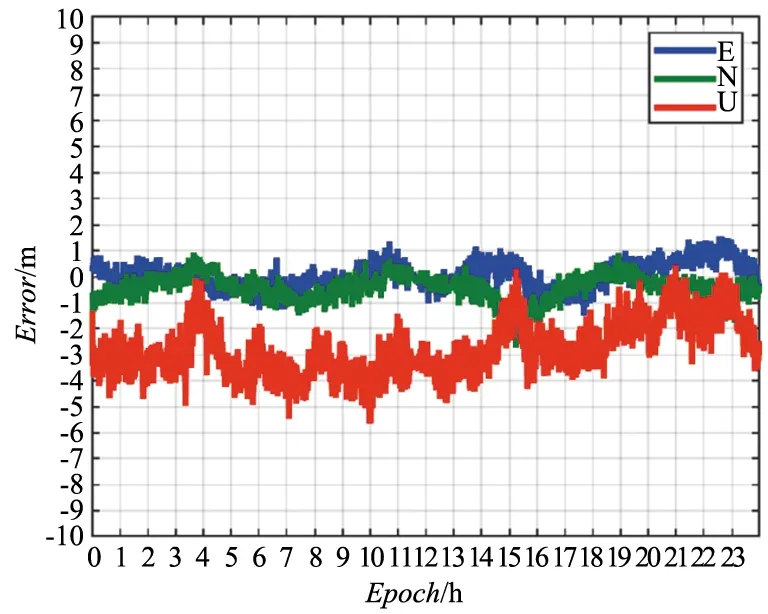
圖4 SGOC測站單頻SPP定位殘差Fig.4 Positioning residual of single-frequency SPP at SGOC station

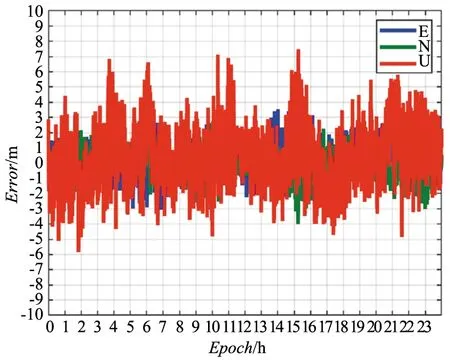
圖5 SGOC測站雙頻SPP定位殘差Fig.5 Positioning residual of dual-frequency SPP at SGOC station

三頻SPP定位殘差如圖6所示。由圖6可以看出，BDS-3/BDS-2三頻偽距單點定位殘差較大，定位精度比單、雙頻偽距單點定位差，是因為三頻定位模型比較粗糙，不能提高定位精度，會使定位精度變差。

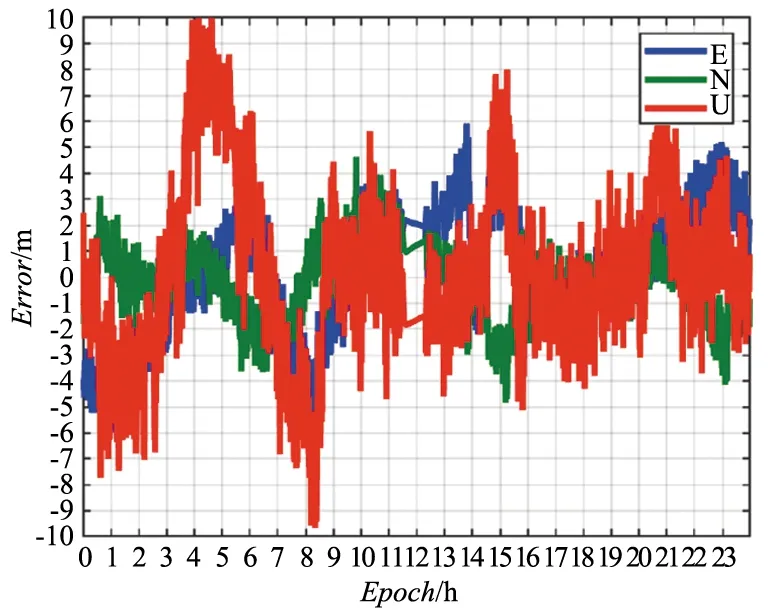
圖6 SGOC測站三頻SPP定位殘差Fig.6 Positioning residual of three-frequency SPP at SGOC station

為進一步分析BDS-3/BDS-2單、雙、三頻偽距單點定位模型性能，圖7給出了各測站的平均RMS的柱狀統計圖，便于更直觀地看出BDS-3/BDS-2單、雙、三頻偽距單點定位模型性能。

圖7 BDS-3/BDS-2單、雙、三頻SPP平均RMSFig.7 Mean RMS of BDS-3/BDS-2 single-,dual- and three-frequency SPP

表1給出BDS-3/BDS-2單、雙、三頻偽距單點定位ENU方向平均RMS。由表1可以看出，單頻偽距單點定位ENU方向精度為0.631，0.863，4.279 m。雙頻偽距單點定位ENU方向精度為1.257，1.221，3.097 m。三頻偽距單點定位ENU方向精度2.102，2.380，4.612 m。

表1 BDS-3/BDS-2單、雙、三頻SPP平均RMS/m

綜合圖表可以看出，單頻偽距單點定位模型在平面方向上表現出的性能更佳，雙頻偽距單點定位模型在高程方向上表現出的性能更佳，三頻偽距單點定位模型在平面方向和高程方向表現出的性能都明顯差于單，雙頻偽距單點定位模型。

3 結束語

首先對單、雙、三頻偽距單點定位的基本原理進行了描述。從原理中得出，雙頻主要是利用無電離層組合消除電離層誤差影響，三頻的消電離層組合模型為構造一個三頻線性組合。此時可以推論出，雙頻偽距單點定位模型利用無電離層組合消除電離層誤差，理論上會提高U方向精度；三頻偽距單點定位模型構建了一個三頻線性組合，理論上三頻消電離層模型粗糙，會降低定位精度。

為驗證上述猜想，基于抗差理論并利用MEGX多站觀測數據對BDS-3/BDS-2單、雙、多頻偽距定位性能進行詳細對比分析，證實上述猜想正確。得到結論：① 在電離層延遲誤差較大的情況下，雙頻偽距單點定位能夠有效抵抗電離層誤差影響，提高U方向定位精度；② 由于偽距單點定位誤差模型簡單，三頻消電離層組合模型擴大噪聲影響降低定位精度。

本文得出的結論具有一定的創新性，為日后研究BDS-3偽距單點定位的學者們提供了一定的參考價值。今后的研究方向將會考慮如何提高三頻偽距單點定位的定位精度。