姿軌控發(fā)動機常平架軸承孔銑加工誤差分析
張曉峰 李旭光 劉 俊
姿軌控發(fā)動機常平架軸承孔銑加工誤差分析
張曉峰 李旭光 劉 俊
(西安航天發(fā)動機有限公司,西安 710100)
針對姿軌控發(fā)動機常平架正交孔系垂直度要求高,加工難以保證的問題,基于齊次坐標變換方法,建立了五軸加工中心調(diào)頭加工常平架軸承孔的垂直度誤差模型。結(jié)合MATLAB計算軟件,對常平架的垂直度誤差進行了定量分析,實現(xiàn)了常平架垂直度誤差影響因素的預測。針對模型設計加工試驗,試驗結(jié)果表明,理論計算和實際加工具有較好的一致性,該方法對常平架加工誤差的控制具有一定指導作用。
常平架;軸承孔;垂直度;齊次坐標變換;誤差模型
1 引言
常平架是液體火箭發(fā)動機實現(xiàn)搖擺,達到對推力矢量進行方向控制,獲得導彈或火箭控制力的關鍵部件[1]。某型號雙向搖擺發(fā)動機所用的常平架為方環(huán)形結(jié)構(gòu),其兩對軸承孔呈正交布置。為實現(xiàn)推力矢量精確控制,兩對軸承孔軸線,即擺動軸線垂直度要求為0.05。常平架的軸線通常被選作發(fā)動機總體布局和裝配的基準,其他搖擺環(huán)節(jié)也以它為基準進行布置[1],若兩個擺動方向軸線垂直度超差,傳遞的推力矢量會產(chǎn)生偏差,積累到推力室噴口位置的推力矢量誤差會更大,直接影響整個發(fā)動機的姿態(tài)控制。因此對常平架軸承孔垂直度誤差模型展開深入研究,以進一步提高常平架加工精度和批次一致性至關重要。
2 工藝難點分析
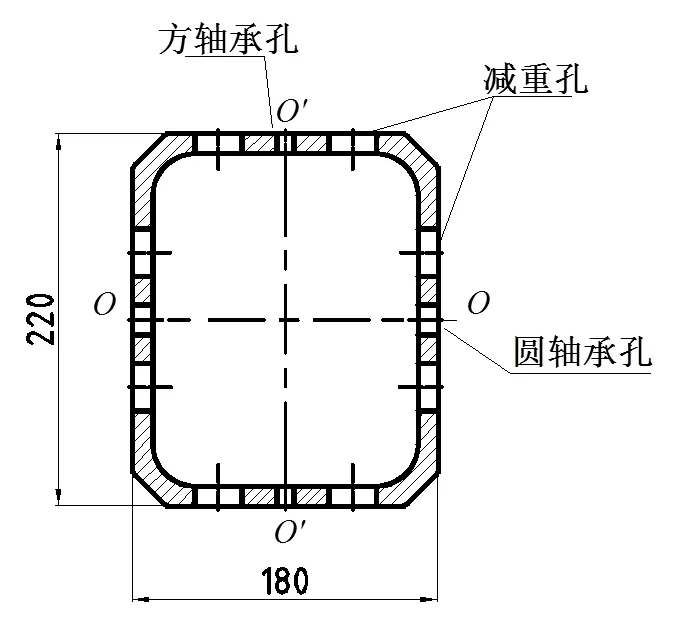
圖1 常平架結(jié)構(gòu)圖
常平架的兩對軸承孔分別為一對方孔和一對圓孔,如圖1所示,兩對軸承孔軸線垂直度要求為0.05。方孔由線切割加工,圓孔在加工中心上銑加工。由于方孔和圓孔分兩次裝夾加工而成,且零件外形大,軸線距離較長:兩方孔間距離220mm,兩圓孔間距離180mm,導致研制過程中出現(xiàn)垂直度0.05難以保證的難題。加工誤差為多體系統(tǒng)問題,前期已對裝夾方式和找正方法進行過多次優(yōu)化,研究機床精度對常平架垂直度的影響。誤差防止是常用的提高機床加工精度的方式[2,3],通常加工誤差建模方式為基于齊次坐標變換和多體系統(tǒng)理論的誤差建模[4,5]。本文的垂直度誤差模型采用齊次坐標變換的建模方法,建立常平架正交孔系垂直度誤差模型,對垂直度誤差進行定量分析,并分析機床轉(zhuǎn)臺誤差對垂直度誤差的影響。
3 基于齊次坐標變換的垂直度誤差模型
3.1 加工中心轉(zhuǎn)臺誤差分析
常平架的一對方孔和一對圓孔在四方形框架上成正交分布。′-′方向的一對方孔受工藝條件限制,由線切割加工而成。隨后在轉(zhuǎn)臺式五軸加工中心上利用專用夾具裝夾,借助專用工裝找正方孔軸線,轉(zhuǎn)臺轉(zhuǎn)90°對第一個圓孔銑加工,隨后轉(zhuǎn)180°對第二個圓孔銑加工。由加工過程可知,轉(zhuǎn)臺誤差是常平架垂直度加工誤差的最主要因素,分析轉(zhuǎn)臺誤差對常平架正交孔系垂直度誤差影響。
在轉(zhuǎn)臺-擺頭式五軸加工中心加工圓孔時,機床主軸軸翻轉(zhuǎn)至與待加工孔軸線平行,機床的加工坐標系轉(zhuǎn)換如圖2a所示。轉(zhuǎn)臺運動副存在6個自由度的運動誤差,如圖2b所示,理想運動是從點轉(zhuǎn)到點,但由于轉(zhuǎn)臺誤差實際運動到了點,這一過程產(chǎn)生6個誤差分量:方向線性誤差Δ、方向線性誤差Δ、方向線性誤差Δ、繞軸角度誤差Δ、繞軸角度誤差Δ、繞軸角度誤差Δ。
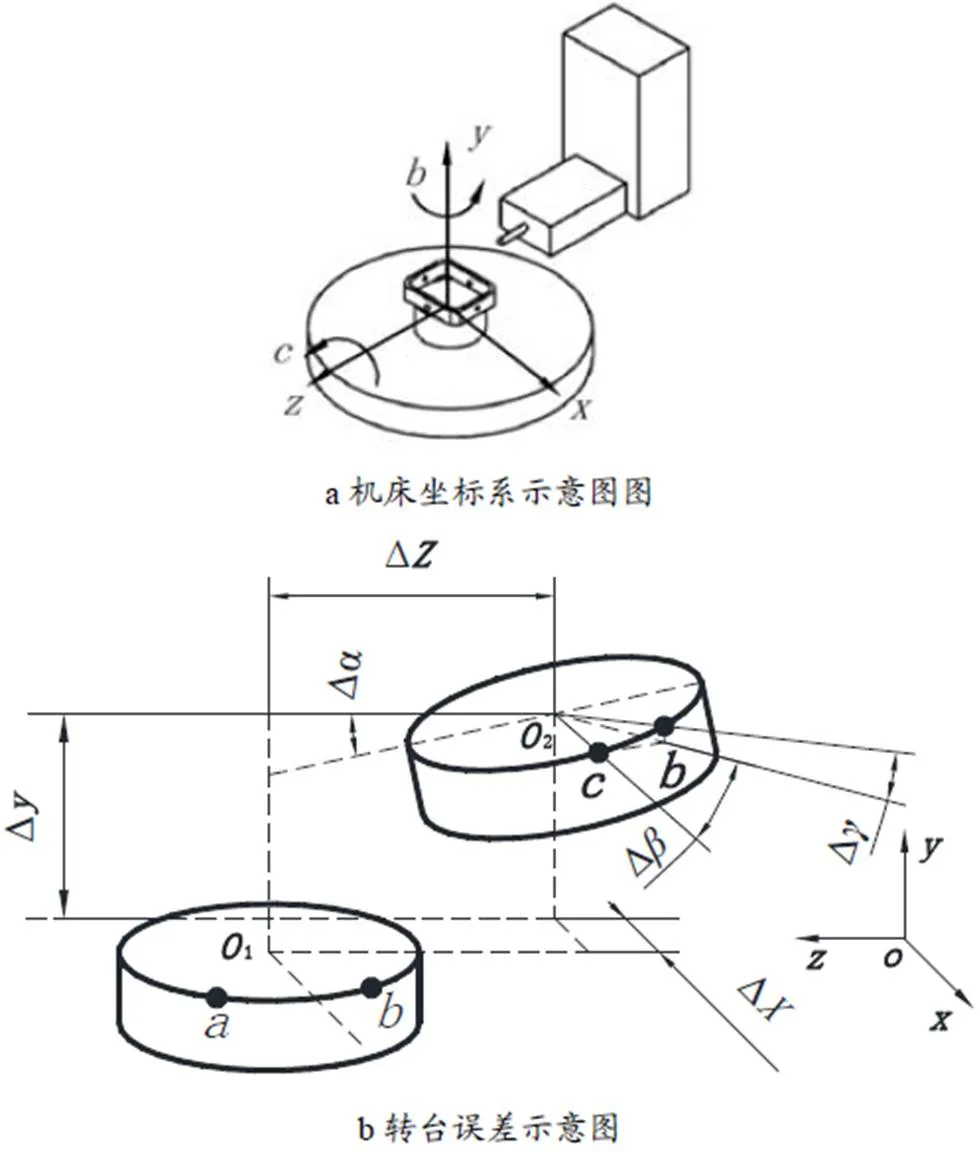
圖2 機床坐標系及轉(zhuǎn)臺誤差示意圖
3.2 基于齊次坐標變換的加工誤差建模
齊次坐標變換可以用來分析空間矢量在不同坐標系間的變換問題。轉(zhuǎn)臺繞軸旋轉(zhuǎn)時,齊次變換矩陣為[6,7]:
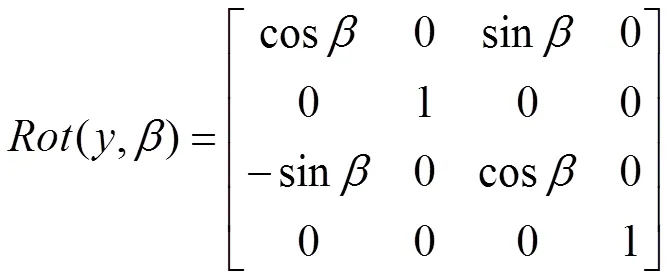
圖2b中,從(1,1,1)點繞軸旋轉(zhuǎn)到(2,2,2),但由于轉(zhuǎn)臺運動誤差實際到了(3,3,3),考慮轉(zhuǎn)臺的三個位移誤差Δ、Δ、Δ和三個角誤差Δ、Δ、Δ引起的綜合變換矩陣,實際空間運動矩陣為:
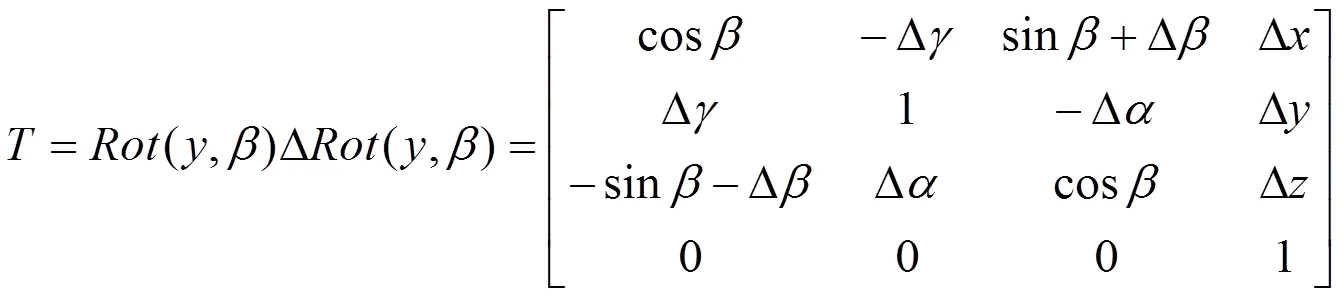
由式(2)可進一步推導出從(1,1,1)點繞軸旋轉(zhuǎn)后實際點(3,3,3)與點的關系為:
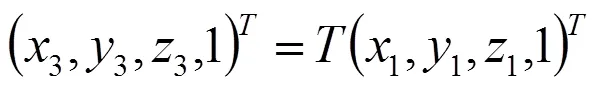
3.3 常平架垂直度誤差模型
常平架銑加工圓孔加工過程如圖3所示。常平架加工圓孔時以方孔軸線為基準。在方孔中穿入專用工裝方軸以找正基準軸線′-′,方軸和方孔采用過渡配合。為最大限度提高找正準確性,采用消除方軸和方孔間隙的辦法,用柔性介質(zhì)橡皮泥從一端固定方軸。出于這一過程操作方便考慮,初始裝夾位置如圖3a所示,方軸大致平行于軸。
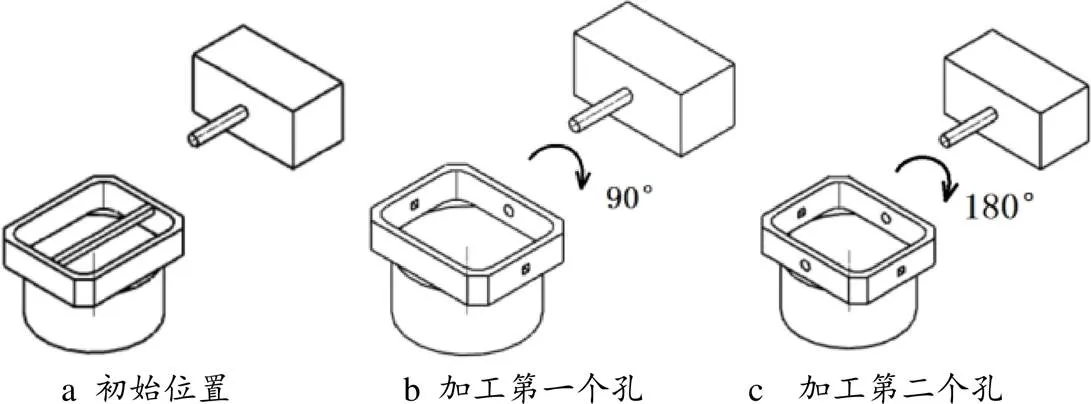
圖3 常平架銑孔過程示意圖
利用百分表找正后方軸理論上完全平行于軸。隨后轉(zhuǎn)臺繞軸旋轉(zhuǎn)1-(π/2),由軸正方向看繞順時針旋轉(zhuǎn),所以1取負值。此時完成第一個圓孔的加工,如圖3b所示。隨后轉(zhuǎn)臺繞軸旋轉(zhuǎn)2=-,完成第二個孔的加工,如圖3c所示。設加工坐標系原點與零件幾何中心重合,第一個孔初始點位置0(0,0,0),旋轉(zhuǎn)1后理論加工位置為1(1,1,1),實際位置為1′(1′1′1′)。完成第一個孔加工,旋轉(zhuǎn)2后理論加工位置為2(222),實際位置為2′(2′2′2′)。基于誤差一致性假設,即兩次旋轉(zhuǎn)產(chǎn)生的位移誤差和角誤差相同,則由式(3)可得:
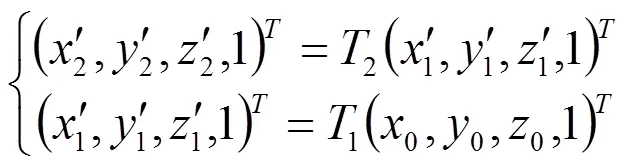
圖4 垂直度誤差模型示意圖
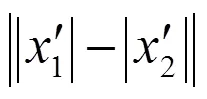
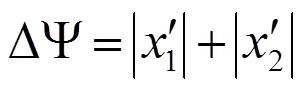
將1-(π/2)、2=-π、(0,00)=(-2, 0, 0)及式(2)、式(3)代入式(4),并將計算結(jié)果代入公式(5),可得垂直度與轉(zhuǎn)臺位移誤差、角誤差的關系:
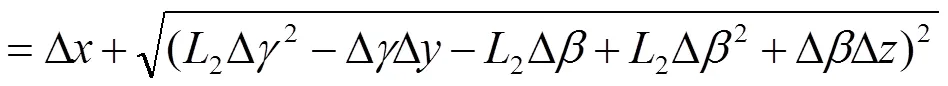
4 同軸度誤差計算
4.1 誤差模型工程轉(zhuǎn)化
機床精度檢測時,轉(zhuǎn)臺精度通常有以下衡量指標:臺面徑向跳動誤差、臺面軸向跳動誤差e、平面度誤差、分度精度和重復精度。在上述理論計算中,轉(zhuǎn)臺誤差分為位移誤差和角誤差,由圖5可以看出轉(zhuǎn)臺精度指標與誤差的轉(zhuǎn)換關系為:Δe、Δe、Δe、Δarcsin[e/22]、Δe、Δarcsin[e/21]。
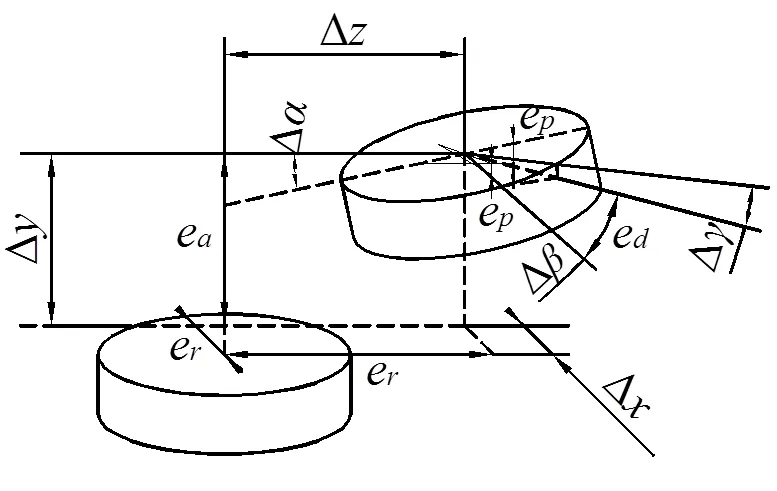
圖5 轉(zhuǎn)臺精度與誤差關系示意圖
將上述換算關系代入式(6),可以得到垂直度誤差的工程模型:
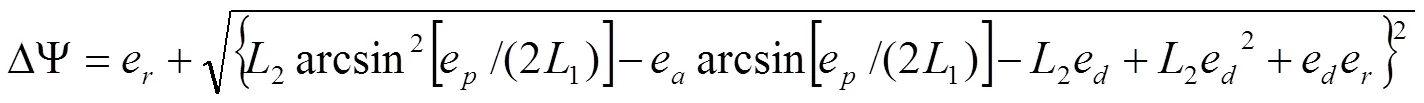
4.2 基于轉(zhuǎn)臺誤差的同軸度誤差計算
a 軸向跳動和徑向跳動對垂直度影響
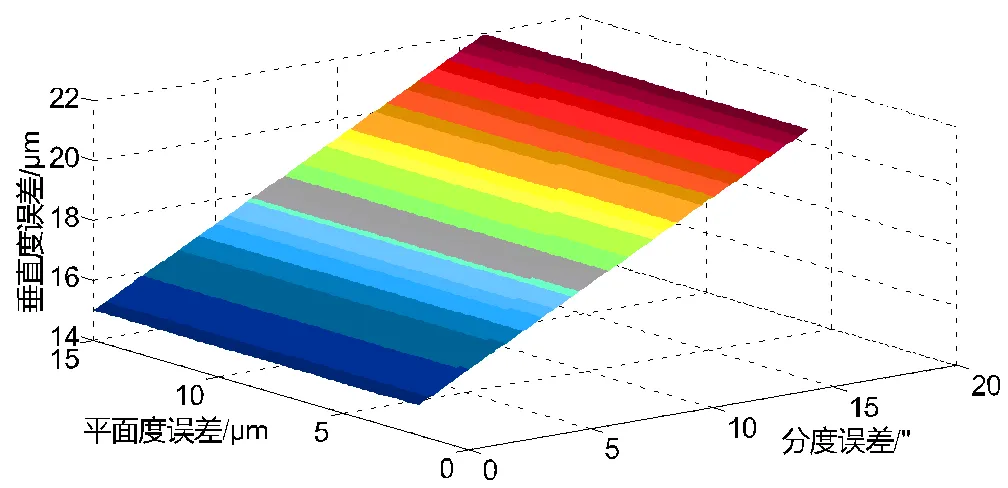
b 平面度和分度對垂直度影響
c 軸向跳動和分度對垂直度影響
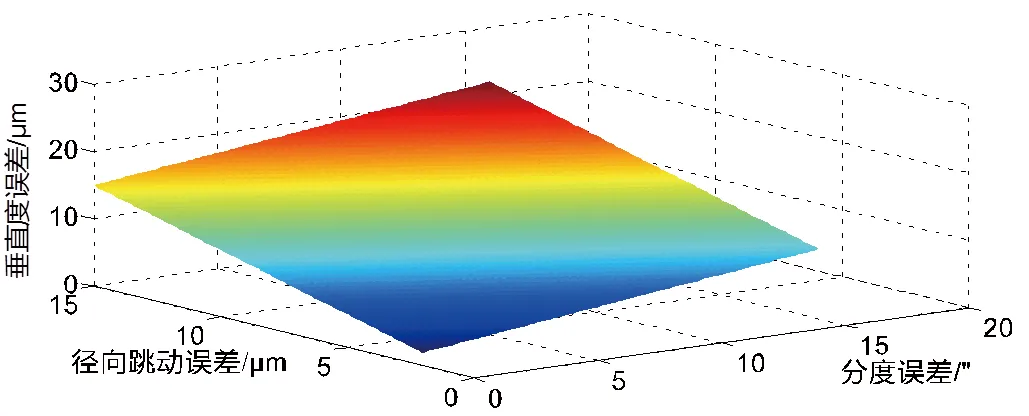
d 徑向跳動和分度對垂直度影響
e 平面度和軸向跳動對垂直度影響
圖6 垂直度誤差和轉(zhuǎn)臺精度指標三維圖
為評估加工中心能否滿足常平架加工誤差,分析轉(zhuǎn)臺各精度指標對加工精度的影響規(guī)律,利用MATLAB工程計算軟件分析垂直度誤差模型。分析計算結(jié)果,由圖6a、圖6b、圖6c可以看出,臺面徑向跳動誤差、分度精度對孔軸線垂直度的影響要遠大于臺面軸向跳動誤差e和平面度誤差。由圖6d可以看出,徑向跳動誤差和分度精度對垂直度影響作用相當,徑向跳動誤差更為明顯。與實際情況吻合。由圖6e可以看出,平面度誤差對垂直度影響更大。
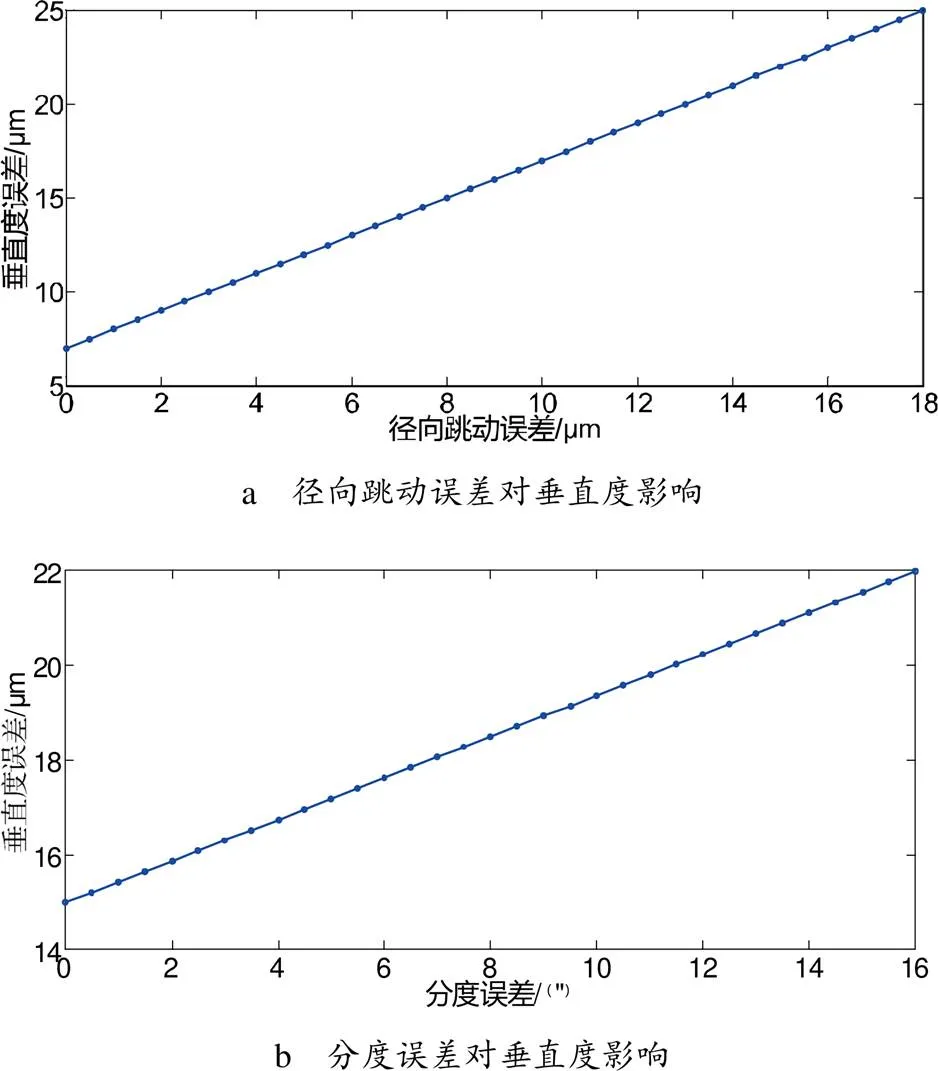
其他三項因素固定,分別分析單因素對垂直度誤差的影響,如圖7a、圖7b、圖7c、圖7d所示,對影響垂直度誤差的影響排序,徑向跳動誤差斜率>分度精度>平面度誤差>軸向跳動誤差。
5 加工試驗
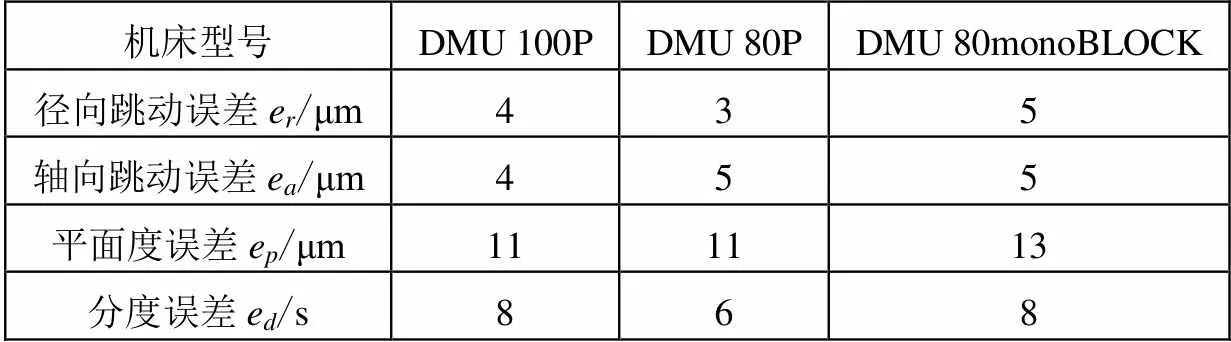
表1 試驗設備轉(zhuǎn)臺精度
在德瑪吉加工中心DMU 100P、DMU 80P、DMU 80monoBLOCK上進行常平架銑圓孔加工試驗,這三臺設備均為轉(zhuǎn)臺-擺頭式五軸加工中心。根據(jù)機床檢測部門提供的檢測數(shù)據(jù),三臺加工中心的轉(zhuǎn)臺精度如表1所示。
在三臺機床上,用同樣的工藝方法和加工參數(shù),分別加工10件常平架,如圖8所示。加工后對試件垂直度進行計量,計量結(jié)果如表2所示。

圖8 常平架加工試驗

表2 試驗件垂直度計量結(jié)果
由加工試驗結(jié)果可以看出:徑向跳動誤差和分度誤差小的機床加工后的常平架垂直度符合公差要求,而軸向跳動誤差和平面度誤差越大,加工后的垂直度不一定越大。從影響程度來看,徑向跳動誤差和分度誤差對垂直度的影響大于平面度誤差和軸向跳動誤差。模型計算與試驗結(jié)果有較好的一致性。
6 結(jié)束語
通過常平架正交孔系垂直度誤差模型的計算和試驗,可以得出以下結(jié)論:
a. 在加工中心轉(zhuǎn)臺的5項精度指標中,徑向跳動誤差和轉(zhuǎn)臺分度誤差是影響垂直度結(jié)果的最關鍵因素,其中徑向跳動誤差的影響更大。
b. 基于齊次坐標變換理論建立的垂直度誤差模型與實際加工結(jié)果具有較好的一致性。
c. 三臺加工中心中,DMU 100P和DMU 80P各項精度指標相當,但DMU 80P由于轉(zhuǎn)臺徑向跳動誤差小,具備轉(zhuǎn)臺分度誤差自動補償功能,加工后的常平架垂直度誤差滿足要求,一致性好,更適合用于常平架銑圓孔的加工。在DMU 80P上加工產(chǎn)品,一批產(chǎn)品加工后的垂直度計量結(jié)果均滿足要求。
1 朱寧昌. 液體火箭發(fā)動機設計(上)[M]. 北京:宇航出版社,1994:277
2 栗時平. 多軸數(shù)控機床精度建模與誤差補償方法研究[D]. 長沙:國防科技大學,2002
3 任永強,楊建國,基里維斯,等. 四軸數(shù)控機床誤差綜合建模原理及分析[J]. 機械工程師,2003(8):18~22
4 徐旭松,楊將新,曹衍龍,等. 基于齊次坐標變換的制造誤差建模研究[J]. 浙江大學學報:工學版,2008,42(6):1021~1026
5 高煥明,楊功流,李星,等. 基于齊次坐標變換的陀螺框架加工誤差分析[J]. 天津大學學報:1017~1020
6 周曉婷. 基于機床誤差建模的加工精度預測研究[D]. 濟南:山東大學,2016:23~24
7 張舒潔. 數(shù)控機床運動誤差分步辨識法理論與實驗研究[D]. 上海:上海交通大學,2010:14
Error Analysis of Bearing Hole Machining of Gimbal Mount Used in Attitude and Orbit Control Engine
Zhang Xiaofeng Li Xuguang Liu Jun
(Xi’an Aerospace Engine Co., Ltd., Xi’an 710100)
The vertical degree of two couple bearing holes of gimbal mount used in attitude and orbit control engine is hard to guaranteed. Based on homogeneous coordinate transformation, a machining error model for the boring of the 5-axis machining center is established. The vertical degree errors are analyzed by the error model using MATLAB software. The test results show that calculation errors are similar to the test data. The error calculation contributes to ensuring accuracy of vertical degree of bearing holes in gimbal mount.
gimbal mount;bearing holes;vertical degree;homogeneous coordinate transformation;error model
V431
A
張曉峰(1991),工程師,航空宇航制造工程專業(yè);研究方向:液體火箭發(fā)動機閥門制造。
2020-12-20

