基于組合核函數的徑向基過程神經網絡及其在示功圖診斷中的應用*
李晶晶,許少華
(山東科技大學計算機科學與工程學院,山東 青島 266590)
1 引言
徑向基函數神經網絡RBFNN(Radial Basis Function Neural Network)是一種廣泛應用于模式識別、函數逼近和信號處理等領域的人工神經網絡模型,它通過改變神經元非線性變換函數的參數實現非線性映射,并通過連接權值調整的線性化來提高網絡學習速度[1-3]。針對時間過程信息的處理問題,文獻[4]將傳統徑向基函數神經網絡向時間域上進行擴展,提出了一種徑向基過程神經網絡RBFPNN(RBF Process Neural Network)。該網絡模型的輸入可以直接為時間過程信號,通過隱層徑向基核函數的時空聚合變換,以及對隱層過程神經元輸出的加權調整,實現對時變信號的分類處理。
復雜信號樣本特征的發現、表征和記憶能力是衡量機器學習模型性能的重要因素,也是在進行模型結構和信息處理機制設計時要考慮的問題。在目前的研究中,RBFPNN的核函數一般取為高斯函數,其性質參數為核寬度,是一種具有局部分布特征的核函數。雖然在理論上由大數定律已證明高斯函數對于各類數據的分析問題具有普適性[5],但由于高斯函數具有局部特性,即與核函數中心特征相似的樣本對結果影響較大,而與核中心相似度低的樣本對結果的影響小,致使對于一些復雜的信號處理問題往往會出現較大的偏差[6],特別是在非線性時間維系統采樣信號具有較強的異構和多峰性、同類樣本呈不同模態變化的情況下。由于徑向基神經網絡主要的信息處理單元為核函數,若通過改變RBFPNN核的函數形式和參數的設置,使其具有在多個尺度上對動態信號過程特征的表征和記憶存儲性質,則可提高RBFPNN對復雜時間信號形態細節特征的識別能力。
針對現有徑向基過程神經網絡在復雜時間信號處理中存在的不足,本文提出了一種基于核函數組合的徑向基過程神經網絡模型。通過將具有全局特性的多項式核函數與具有局部性質的高斯核函數進行組合,構成具有復合分布性質的核函數,使其在對時間信號形態的表征上同時具有局部和全局的尺度性質,即在尺度選擇上具有更好的完整性和靈活性,從而獲得RBFPNN模型對過程信號細節特征的多分辨能力。核函數組合的徑向基過程神經網絡模型可通過典型動態樣本的學習直接獲得輸入函數樣本與模式類別之間的對應關系,而無須事先提取時間信號的形態和幅值特征,對于解決復雜時間信號的分類問題,在信息處理機制上具有良好的適應性。本文分析了組合核函數RBFPNN的性質,建立了基于混沌遺傳算法CGA(Chaos Genetic Algorithm)的模型參數整體優化算法。以基于示功圖的往復運動機械工作狀況診斷分析為例進行仿真實驗,結果表明組合核函數RBFPNN可較大提高識別的準確性。
2 徑向基過程神經網絡模型
徑向基過程神經網絡為一種3層前饋結構模型[4],輸入層有n個節點單元(x1(t),x2(t),…,xn(t)),完成時間信號向網絡的過程輸入;中間徑向基過程神經元隱層有m個節點,節點單元的變換函數是徑向基核函數K;網絡的輸出為隱層節點輸出信號的線性加權和∑,拓撲結構如圖1所示。
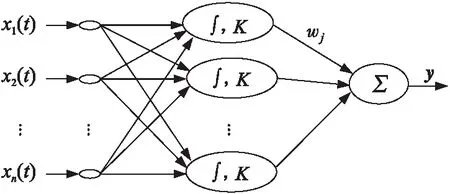
Figure 1 RBF process neural network圖1 徑向基過程神經網絡


(1)
其中,‖·‖為(C[0,T])n空間中的某一距離范數,Zj(t)表示所有徑向基核中心函數組成的序列。
(2)
其中,σ為k個核中心函數的平均距離差,描述了信號集樣本的統計分布性質,其計算方式如式(3)所示:
(3)
(4)
3 組合核函數徑向基過程神經網絡
核函數組合的徑向基過程神經網絡是將具有全局性質的多項式核函數與高斯核函數進行線性組合,使新的核函數同時具有局部和全局的尺度性質,以提高對復雜信號形態特征的表征能力和改善傳統徑向基核函數對時間信號過程特征的記憶和辨識性質。
在時域空間中,多項式核函數定義如下:
Kploy(X(t),Y(t))=((X(t)·Y(t))+c)p
(5)
其中,p>0為指數參數最高次數,c為偏移量參數。
構造一種多項式核函數與高斯核函數自適應組合的核函數:
KMix(X(t),Y(t))=η·KPloy(X(t),Y(t))+
(1-η)·KGau(X(t),Y(t))
(6)
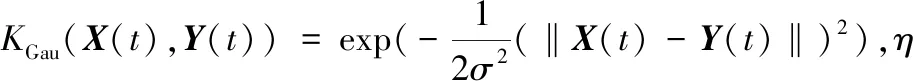
特別地,當c=1時,Kploy(X(t),Y(t))=((X(t)·Y(t))+1)p,多項式核函數僅包含參數p。
式(4)中的核寬度參數和指數參數是通過對訓練樣本集的學習自適應確定的,因此,針對動態模式識別問題,組合核函數兼顧了系統時變信號特征描述的局部性和全局性,可提高BRFPNN對動態輸入樣本與核中心函數模態細節特征差異的表征和相似性度量能力。
在圖1所示的RBFPNN中,以式(4)表示的組合核函數為RBFPNN的徑向基核,基于組合核函數徑向基過程神經網絡的模型圖如圖2所示:
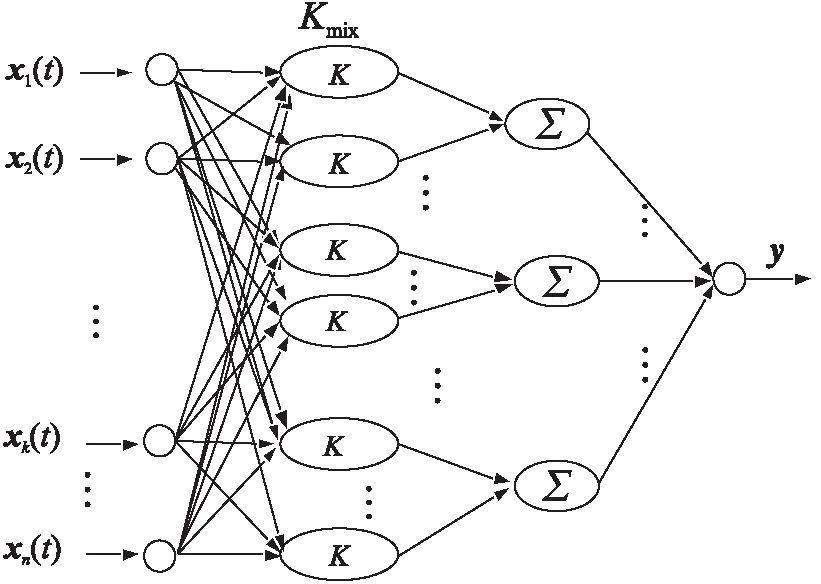
Figure 2 A model of radial basis process neural network based on combined kernel function圖2 基于組合核函數的徑向基過程神經網絡模型
其中,X(t)=(x1(t),x2(t),…,xn(t)),t=0,1,…,T為網絡的數據,則RBFPNN輸入輸出之間的映射關系為:
(7)
其中,zj(t)為第j個徑向基核中心函數,j=1,2,…,m;m為徑向基過程神經元隱層節點數。模型的信息處理流程如下所示:
Step 1過程神經網絡是時空聚合模式的實現,由于時間聚合不容易實現,因而選用walsh正交基函數代替時間聚合運算,選取一組基函數B(t)=(b1(t),b2(t),…,bL(t)),將X(t)的權值系數wj在基函數中展開作為徑向基過程神經網絡的輸入和權值參數,展開形式分別如式(8)和式(9)所示:
(8)
(9)
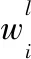
Step 2設置訓練迭代次數及學習誤差參數,初始化權值和閾值參數。
Step 3K表示組合核函數,將具有全局特征的多項式核函數與具有局部特征的高斯函數相結合構成模型的核函數。
Step 4空間聚合運算選擇求和函數∑,權值函數為wj。
Step 5網絡的輸出如式(5)所示。
通過對訓練集樣本的自適應學習,組合核函數徑向基過程神經網絡可更加完整地反映時變過程信號模態細節特征的變化,提高對特征的記憶存儲和辨識能力,降低機器模型的結構風險。
4 組合核函數RBFPNN的優化求解
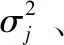
4.1 核中心函數的確定
實際應用中,可利用廣義歐氏距離進行動態樣本間過程特征的相似性度量,采用動態聚類算法,例如K-means聚類算法[7]來確定RBFPNN核中心函數。首先根據廣義歐氏距離度量樣本之間的相似度,初始將聚類數設置為4,然后將聚類后產生的簇中心函數作為典型樣本,即將聚類結果確定的聚類數作為RBFPNN隱層的節點數,聚類中心函數作為徑向基核中心函數。核中心函數zj(t)的表達式如式(6)所示:
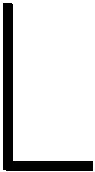
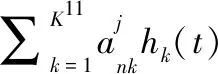
(10)
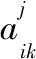
4.2 基于CGA的模型參數優化求解算法
混沌遺傳算法CGA是一種融合遺傳算法進化機制和混沌搜索策略各自優勢的智能算法[10,11],具有群體搜索、軌道遍歷和全局優化等性質。混沌搜索是將混沌狀態引入優化變量中,通過施加混沌擾動,使其在一定范圍內按系統內在規律不重復地遍歷所有狀態[12]。考慮一種基于蟲口模型的混沌序列生成方法,以Logistic映射為發生器,按式(11)產生混沌序列:
δj+1=uδj(1-δj)
(11)
其中,u是混沌吸引子。當u= 4時,系統進入混沌狀態,產生混沌變量δj(j=1,2,…,k),其值在[0,1]內變化。
CGA將混沌運動性質結合進優化變量的搜索中,對得到的混沌變量進行編碼,表示成染色體,并將它們置于問題的環境中,根據適者生存的原則進行選擇、混沌交叉、混沌變異等遺傳操作,通過遺傳迭代的不斷進化,最后收斂到可行解空間中一個最適應環境的個體上,求得問題的全局最優解。CGA算法具體實施步驟如下所示:
Step 1確定種群規模N,隨機生成初始種群G,采用十進制數對染色體進行編碼,每條染色體上基因數為待優化的變量個數;設置最大迭代代數,訓練誤差精度ε。
Step 2構造適應度函數。由于訓練目標為函數極小值優化問題,適應度函數取為fit=e-x,保證適應度函數不為負數。
Step 3選擇操作。在G中采用輪轉規則選擇染色體,每個染色體的被選擇概率正比于其適應度值。
Step 4混沌交叉。2條染色體按如下方式組合:ch′1=λch1+(1-λ)ch2,ch′2=λch2+(1-λ)ch1,其中λ∈(0,1)為混沌變量。一般地,當λ=0.5時,交叉算子效果更好。定義交叉幅值λk,按下式確定λk=λδj+1。為使遍歷呈現雙向性,混沌變量δj+1按下式確定:δj+1=8δj(1-δj)-1。
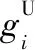
(12)
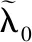
Step 6若滿足終止條件,則保存最優解停機;若不滿足,則轉Step 3。
優化算法流程如圖3所示。
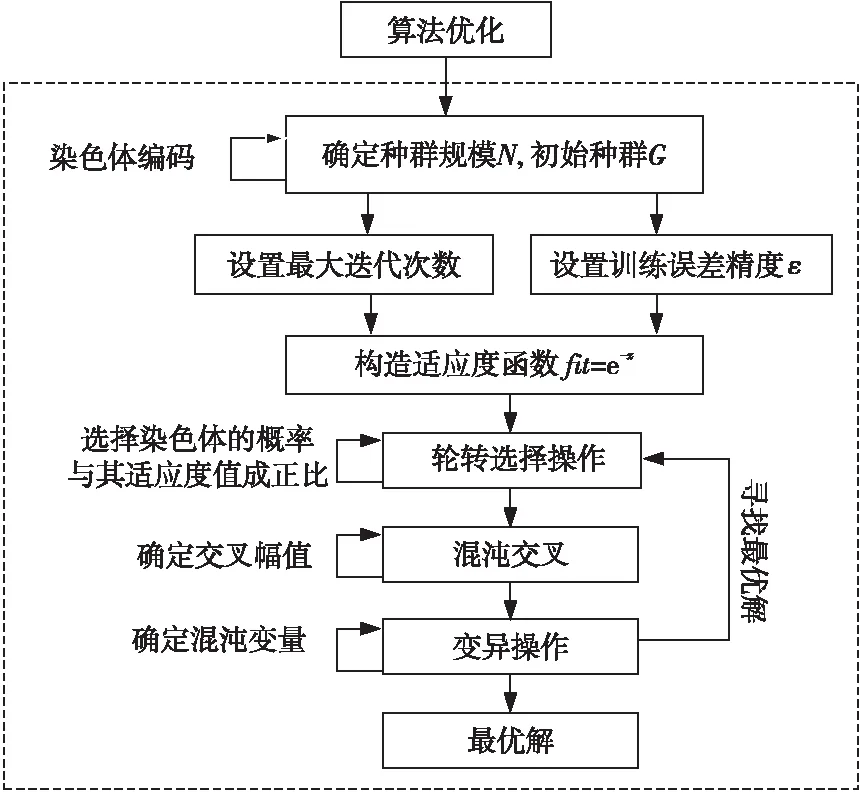
Figure 3 Flowchart of model parameter optimization solution圖3 模型參數優化求解流程
5 仿真實驗分析
泵驅動的往復運動機械是工業制造和交通運輸等領域廣泛使用的重要設備。一些情況下,由于機械工作環境變化大、使用情況復雜,常常導致額定的工作狀態發生改變,使設備產生故障[13]。準確判斷機械當前的工作狀況,及時對機械系統進行維護和工作參數調整,對于降低機械故障風險具有重要的意義。在一個工作周期內選取相同時間的位移和載荷值,由一個沖程的載荷隨位移變化關系所構成的封閉曲線圖稱為往復運動機械的示功圖。位移-時間曲線和載荷-時間曲線以及它們的組合特征反映了示功圖所對應的設備工作狀態,是分析判斷機械系統是否存在故障的重要依據。本文實驗數據來源于大慶油田機械裝備[13],其井況參數設置為:泵徑為38 mm;泵沉沒為433.77 m,沖程為3 m;沖次為9 次/分。國內外現有油井診斷系統大部分采用計算機診斷技術[14,15],示功圖由專門的儀器測量并畫在坐標圖上,泵功圖特征的提取大多采用面積法和矢量法[16]。
在實際資料處理中,選取正常、游動凡爾漏失、碰泵、以及泵吸入和排出漏失等4種不同工作狀態的示功圖共134個樣本,典型示功圖樣本曲線如圖4~圖7所示。
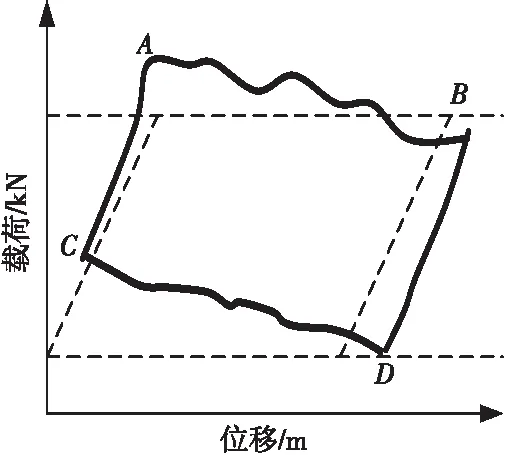
Figure 4 Normal working condition圖4 正常工作情況
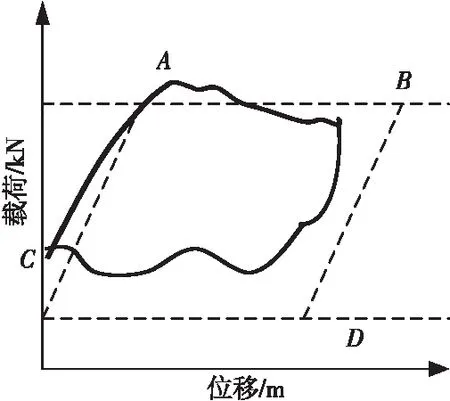
Figure 5 Floating Vernal leakage圖5 游動凡爾漏失
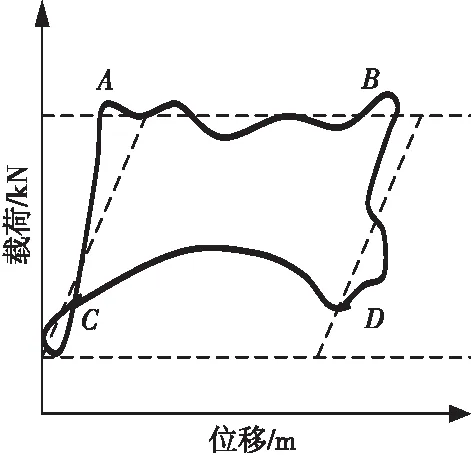
Figure 6 Bump pump圖6 碰泵
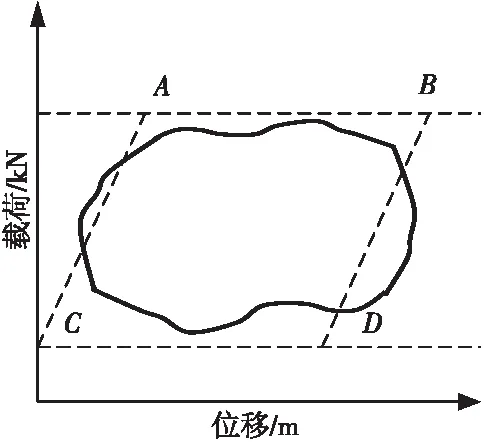
Figure 7 Pump suction and discharge leakage圖7 泵吸入和排出漏失
按比例分別選取30條游動凡爾漏失、25條碰泵、25條泵吸入和排出漏失和10條正常共90條信號樣本組成訓練樣本集,測試集由其余44個樣本組成。由于設備檢測信號為離散采樣數據,采用Walsh正交函數系[8]進行函數擬合,基函數個數L為32時滿足精度0.05的擬合要求。以式(5)定義的組合核函數RBFPNN作為故障自動診斷器,以一個周期內的位移-時間信號和載荷-時間信號作為網絡輸入,輸出為機械工作狀態。由于泵驅動的往復運動機械運行時有3種故障模式,加上正常情況,故組合核函數RBFPNN網絡結構參數[17]選擇如下:2個時間信號輸入節點,4個隱層節點單元,1個故障模式輸出節點。游動凡爾漏失情況輸出對應0.25,碰泵情況對應0.50,泵吸入和排出漏失情況對應0.75,正常狀態對應1.0。示功圖的實驗數據分布情況如表1所示。
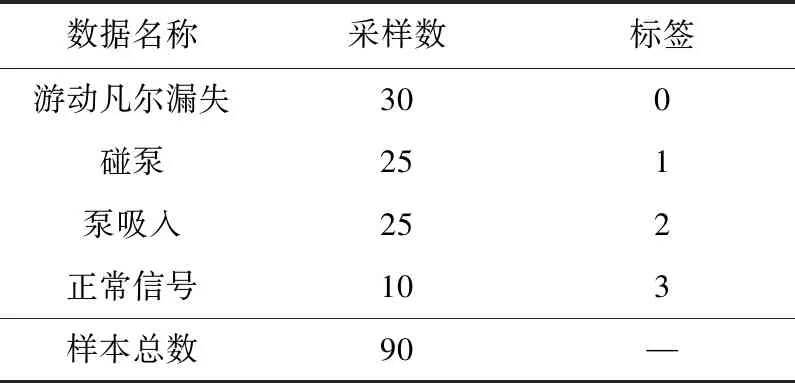
Table 1 Indicator diagram data distribution
以某一條泵漏失信號為例,參數設置如表2所示。
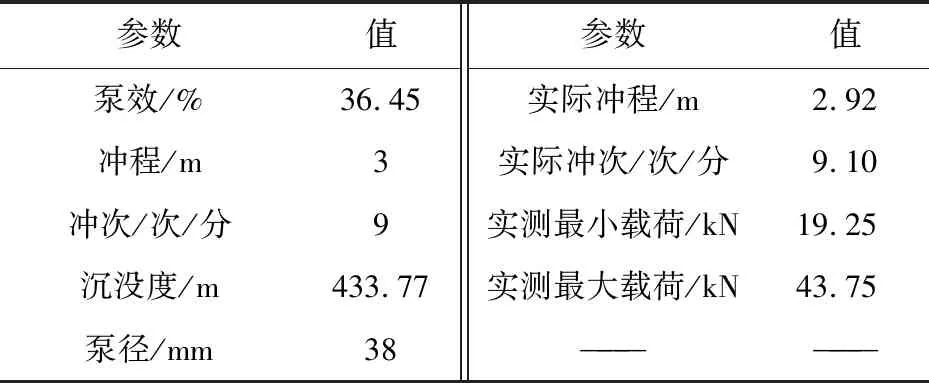
Table 2 Take pump leakage signal as an example of parameter setting
表2顯示了一條泵漏失數據的參數設置,在實驗過程中主要參考泵效、沖程、沖次、沉沒度、最小電荷、最大電荷等參數的判別檢測。由表2得到的示功圖例如圖8所示。
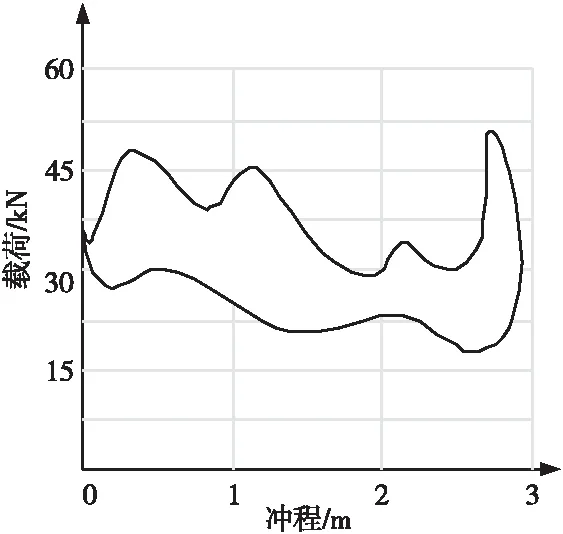
Figure 8 Pump leakage indicator diagram圖8 泵漏失示功圖例
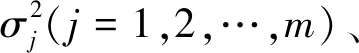
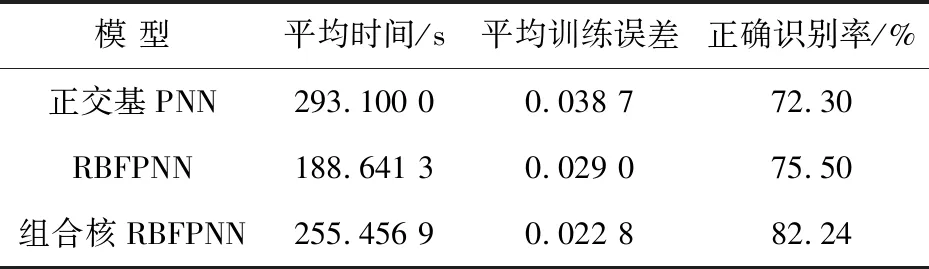
Table 3 Comparison of training and recognition results of the three models
實驗結果表明,本文建立的組合核函數RBFPNN診斷模型相比于PNN和RBFPNN診斷模型,在故障識別精度上有較大提高。這是由于在核函數構造中,組合核函數采用復合分布函數來描述時間信號的數據分布特征,改善了診斷模型對復雜時間信號過程細節特征之間相似性度量性質,較好地實現了對輸入信號模態特征更精確的辨識,達到了較為理想的結果。
6 結束語
本文提出了一種基于核函數組合的徑向基過程神經網模型和算法。模型從結構上擴展了對時變信號形態特征的表征和記憶功能,改善了RBFPNN對動態樣本復雜模態細節特征之間的相似性度量性質,提高了分析模型對信號過程特征的捕獲和辨識能力,仿真實驗取得了較好結果。但是,由于組合核函數增加了尺度參數,使得網絡計算復雜度提高了,因此,如何改善模型學習效率是徑向基神經網絡在時間維空間信號處理中下一步要研究的重要課題。

